C2.1 - Stochastik
1
In einem Paketzentrum werden pro Jahr viele Millionen Pakete angeliefert. Die Pakete werden automatisch nach ihrem Bestimmungsort sortiert.  der Pakete haben das Ziel
der Pakete haben das Ziel 
 das Ziel
das Ziel  Die übrigen Pakete haben andere Ziele.
Die übrigen Pakete haben andere Ziele.
1.1
Bestimme unter Angabe einer geeigneten Zufallsvariablen  die Wahrscheinlichkeit dafür, dass von 100 zufällig ausgewählten Paketen
die Wahrscheinlichkeit dafür, dass von 100 zufällig ausgewählten Paketen
genau neun das Ziel  haben,
haben,
weniger als neun das Ziel  haben.
haben.
(3 BE)
1.2
Unter 100 zufällig ausgewählten Paketen haben genau neun das Ziel  .
.
Berechne die prozentuale Abweichung dieser Anzahl vom Erwartungswert für die Anzahl von Paketen mit dem Ziel unter 100 zufällig ausgewählten Paketen.
unter 100 zufällig ausgewählten Paketen.
Berechne die prozentuale Abweichung dieser Anzahl vom Erwartungswert für die Anzahl von Paketen mit dem Ziel
(3 BE)
1.3
Im Paketzentrum werden 20 Pakete zufällig ausgewählt.
1.3.1
Die Wahrscheinlichkeit dafür, dass von den 20 ausgewählten Paketen keines das Ziel  hat, beträgt etwa
hat, beträgt etwa  . Berechne den Anteil der Pakete mit dem Ziel
. Berechne den Anteil der Pakete mit dem Ziel  unter allen Paketen, die pro Jahr im Paketzentrum angeliefert werden.
unter allen Paketen, die pro Jahr im Paketzentrum angeliefert werden.
(3 BE)
1.3.2
Die Wahrscheinlichkeit eines Ereignisses im Sachzusammenhang kann mit dem Term  berechnet werden. Gib ein passendes Ereignis an.
berechnet werden. Gib ein passendes Ereignis an.
(2 BE)
2
Alle im Paketzentrum angelieferten Pakete werden im Rahmen der Sortierung gewogen.  der Pakete haben eine Masse von mehr als
der Pakete haben eine Masse von mehr als  und gelten damit als schwer. Von den Paketen mit dem Ziel
und gelten damit als schwer. Von den Paketen mit dem Ziel  sind
sind  schwer. Weiterhin haben
schwer. Weiterhin haben  der Pakete das Ziel
der Pakete das Ziel  und
und  das Ziel
das Ziel  .
.
Ein Paket wird zufällig ausgewählt. Betrachtet werden die folgenden Ereignisse:


Ein Paket wird zufällig ausgewählt. Betrachtet werden die folgenden Ereignisse:
„Das ausgewählte Paket ist schwer.“
„Das ausgewählte Paket hat das Ziel A.“
2.1
Stelle den Sachzusammenhang in einer vollständig ausgefüllten Vierfeldertafel dar.
(3 BE)
2.2
Untersuche, ob der Anteil der Pakete mit dem Ziel  unter den schweren Paketen ebenso groß ist wie unter den Paketen, die nicht schwer sind.
unter den schweren Paketen ebenso groß ist wie unter den Paketen, die nicht schwer sind.
(3 BE)
2.3
Von den Paketen, die das Ziel  haben, sind
haben, sind  schwer. Entscheide, ob der Anteil der schweren Pakete unter denjenigen, die weder das Ziel
schwer. Entscheide, ob der Anteil der schweren Pakete unter denjenigen, die weder das Ziel  noch das Ziel
noch das Ziel  haben, kleiner als
haben, kleiner als  , gleich
, gleich  oder größer als
oder größer als  ist. Begründe deine Entscheidung, ohne diesen Anteil zu berechnen.
ist. Begründe deine Entscheidung, ohne diesen Anteil zu berechnen.
(3 BE)
2.4
Im Paketzentrum wird ein schweres Paket zufällig ausgewählt und in einen Lkw verladen.
Bestimme die Wahrscheinlichkeit dafür, dass es sich um ein Paket handelt, das nicht das Ziel hat.
hat.
Bestimme die Wahrscheinlichkeit dafür, dass es sich um ein Paket handelt, das nicht das Ziel
(3 BE)
2.5
Im Rahmen der Sortierung werden die Pakete in zufälliger Reihenfolge ausgewählt und gewogen.
Berechne die Anzahl der Pakete, die mindestens gewogen werden müssen, damit mit einer Wahrscheinlichkeit von mindestens mindestens ein schweres Paket darunter ist.
mindestens ein schweres Paket darunter ist.
Berechne die Anzahl der Pakete, die mindestens gewogen werden müssen, damit mit einer Wahrscheinlichkeit von mindestens
(4 BE)
2.6
Die Zufallsgröße  gibt die Anzahl der schweren Pakete unter insgesamt
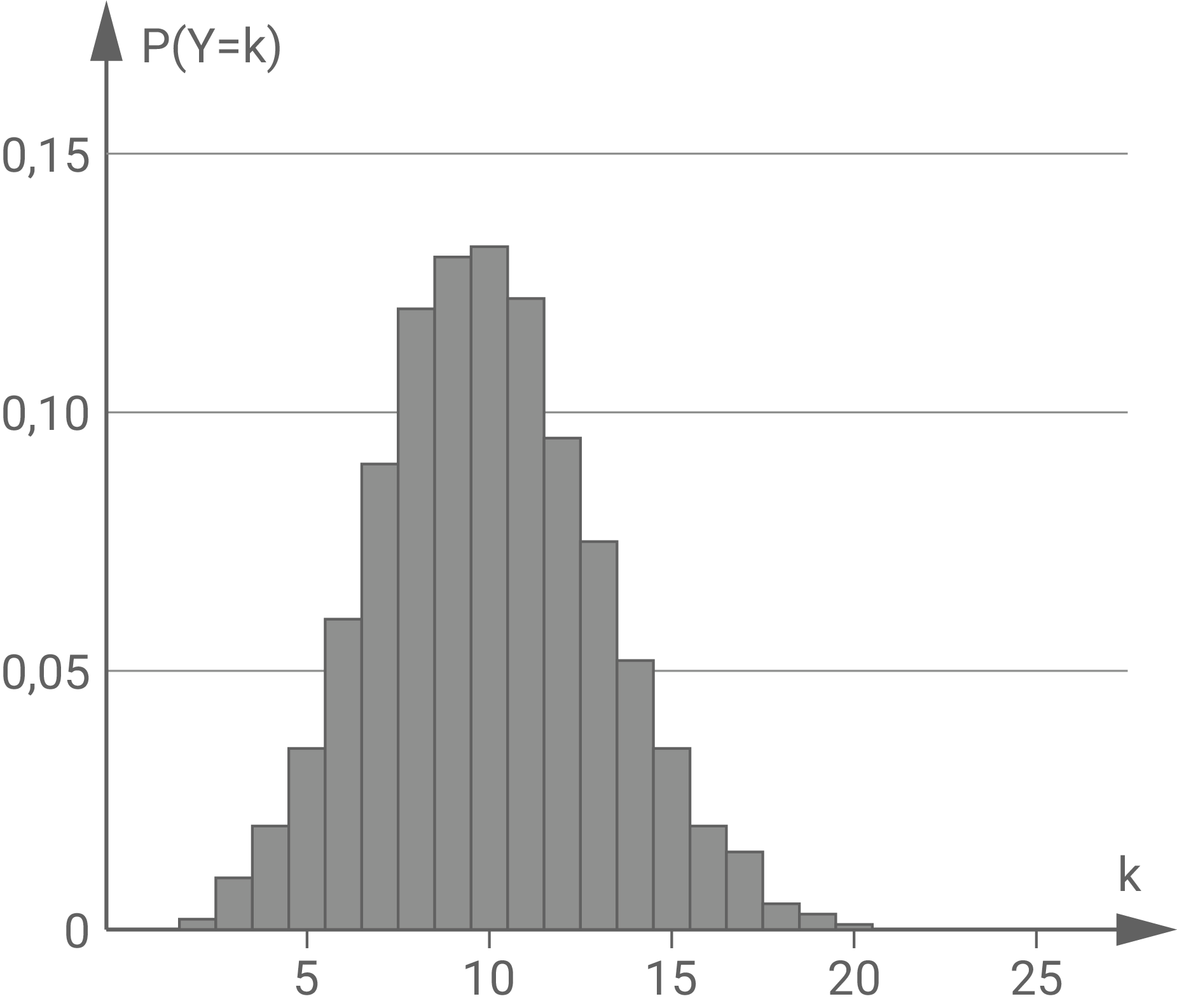
gibt die Anzahl der schweren Pakete unter insgesamt  zufällig ausgewählten Paketen an. Im Material ist die Wahrscheinlichkeitsverteilung von
zufällig ausgewählten Paketen an. Im Material ist die Wahrscheinlichkeitsverteilung von  für einen bestimmten Wert von
für einen bestimmten Wert von  dargestellt. Hierbei ist der Erwartungswert
dargestellt. Hierbei ist der Erwartungswert  eine natürliche Zahl. Bestätige mithilfe des Materials, dass
eine natürliche Zahl. Bestätige mithilfe des Materials, dass  gilt.
gilt.
Bestimme die Gesamtzahl der Pakete.
der Pakete.
Bestimme die Gesamtzahl

Material
(5 BE)
3
Auf einem Rollcontainer befinden sich 100 Pakete, darunter 30 Pakete für den Eulerplatz, 45 Pakete für die Gaußstraße und 25 Pakete für den Leibnizweg. Die Pakete sind im Container zufällig angeordnet.
Ein Paketzusteller lädt 5 Pakete vom Container; darunter befinden sich 3 Pakete für den Eulerplatz und 2 Pakete für den Leibnizweg. Zur Bestimmung der Wahrscheinlichkeit für dieses Ereignis werden 4 Ansätze aufgestellt.







 Entscheide für jeden der Ansätze, ob er richtig oder falsch ist, und begründe jeweils deine Entscheidung.
Entscheide für jeden der Ansätze, ob er richtig oder falsch ist, und begründe jeweils deine Entscheidung.
Ein Paketzusteller lädt 5 Pakete vom Container; darunter befinden sich 3 Pakete für den Eulerplatz und 2 Pakete für den Leibnizweg. Zur Bestimmung der Wahrscheinlichkeit für dieses Ereignis werden 4 Ansätze aufgestellt.
(8 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
Sei  die Anzahl der Pakete, welche das Ziel
die Anzahl der Pakete, welche das Ziel  haben.
haben.
 ist binomialverteilt mit
ist binomialverteilt mit  und
und  Wahrscheinlichkeit, dass genau neun Pakete das Ziel
Wahrscheinlichkeit, dass genau neun Pakete das Ziel  haben:
haben:
 Wahrscheinlichkeit, dass weniger als neun Pakete das Ziel
Wahrscheinlichkeit, dass weniger als neun Pakete das Ziel  haben:
haben:

1.2
1. Schritt: Erwartungswert berechnen
 2. Schritt: Prozentuale Abweichung
2. Schritt: Prozentuale Abweichung  bestimmen
bestimmen

1.3.1
Sei  die Anzahl der Pakete, welche das Ziel
die Anzahl der Pakete, welche das Ziel  haben.
haben.
 ist binomialverteilt mit
ist binomialverteilt mit  und
und 
 Mit dem CAS folgt:
Für
Mit dem CAS folgt:
Für  ergibt sich
ergibt sich  Somit haben
Somit haben  der angelieferten Pakete das Ziel
der angelieferten Pakete das Ziel 
1.3.2
Von 20 Paketen haben die ersten 14 Pakete nicht das Ziel  Von den restlichen 6 Paketen haben höchstens 3 Pakete das Ziel
Von den restlichen 6 Paketen haben höchstens 3 Pakete das Ziel 
2
| Gesamt | |||
|---|---|---|---|
| Gesamt |
2.2
Anteil der Pakete  unter den schweren Paketen:
unter den schweren Paketen:
 Anteil der Pakete
Anteil der Pakete  unter den Paketen, die nicht schwer sind:
unter den Paketen, die nicht schwer sind:
 Der Anteil der Pakete
Der Anteil der Pakete  unter den schweren Paketen ist folglich nicht genauso groß wie der Anteil unter den Paketen, die nicht schwer sind, sondern größer als dieser.
unter den schweren Paketen ist folglich nicht genauso groß wie der Anteil unter den Paketen, die nicht schwer sind, sondern größer als dieser.
2.3
Unter allen Paketen ist der Anteil derer mit dem Ziel A größer als der Anteil derer mit dem Ziel B. Damit ist der Anteil der schweren Pakete unter denen mit den Zielen A und B insgesamt größer als  . Der Anteil der schweren Pakete unter denjenigen, die weder das Ziel A noch das Ziel B haben, ist also kleiner als
. Der Anteil der schweren Pakete unter denjenigen, die weder das Ziel A noch das Ziel B haben, ist also kleiner als 
 Aufgelöst nach
Aufgelöst nach  ergibt sich:
ergibt sich: 

2.4
2.5
2.6
Wenn  gelten würde, müssten die Säulen des Diagramms für die Werte 10 bis 12 durchschnittlich etwa
gelten würde, müssten die Säulen des Diagramms für die Werte 10 bis 12 durchschnittlich etwa  betragen.
Aus dem Material kann jedoch entnommen werden, dass dies nicht der Fall ist.
Folglich muss gelten:
betragen.
Aus dem Material kann jedoch entnommen werden, dass dies nicht der Fall ist.
Folglich muss gelten:  Gesamtzahl
Gesamtzahl  bestimmen
Dem Material kann der Erwartungswert
bestimmen
Dem Material kann der Erwartungswert  entnommen werden.
Mit
entnommen werden.
Mit  und
und  folgt:
folgt:
 Die Gesamtzahl
Die Gesamtzahl  der Pakete beträgt somit 200.
der Pakete beträgt somit 200.
3
Ansatz  Dieser Ansatz ist falsch.
Es wird zwar berücksichtigt , dass die Gesamtanzahl nach dem Herausnehmen eines Pakets geringer wird, jedoch wird so nur der Fall betrachtet, in welchem zuerst die beiden Pakete des Leibnizwegs und anschließend die 3 Pakete für den Eulerplatz herausgenommen werden.
Ansatz
Dieser Ansatz ist falsch.
Es wird zwar berücksichtigt , dass die Gesamtanzahl nach dem Herausnehmen eines Pakets geringer wird, jedoch wird so nur der Fall betrachtet, in welchem zuerst die beiden Pakete des Leibnizwegs und anschließend die 3 Pakete für den Eulerplatz herausgenommen werden.
Ansatz  Dieser Ansatz ist richtig.
Es wird die Anzahl möglicher passender Ereignisse berechnet und durch die Gesamtanzahl der Ereignisse geteilt. Dies stellt die gesuchte Wahrscheinlichkeit dar.
Ansatz
Dieser Ansatz ist richtig.
Es wird die Anzahl möglicher passender Ereignisse berechnet und durch die Gesamtanzahl der Ereignisse geteilt. Dies stellt die gesuchte Wahrscheinlichkeit dar.
Ansatz  Dieser Ansatz ist richtig.
Er bezieht sich sowohl auf die abnehmende Gesamtzahl der Pakete im Container als auch auf die Anzahl der Möglichkeiten, in welcher Reihenfolge die Pakete entnommen werden.
Ansatz
Dieser Ansatz ist richtig.
Er bezieht sich sowohl auf die abnehmende Gesamtzahl der Pakete im Container als auch auf die Anzahl der Möglichkeiten, in welcher Reihenfolge die Pakete entnommen werden.
Ansatz  Dieser Ansatz ist falsch.
Er berücksichtigt nicht, dass sich nach dem Herausnehmen eines Pakets die Wahrscheinlichkeiten für die verschiedenen Zustellungsorte verändern.
Dieser Ansatz ist falsch.
Er berücksichtigt nicht, dass sich nach dem Herausnehmen eines Pakets die Wahrscheinlichkeiten für die verschiedenen Zustellungsorte verändern.