B1 - Analysis

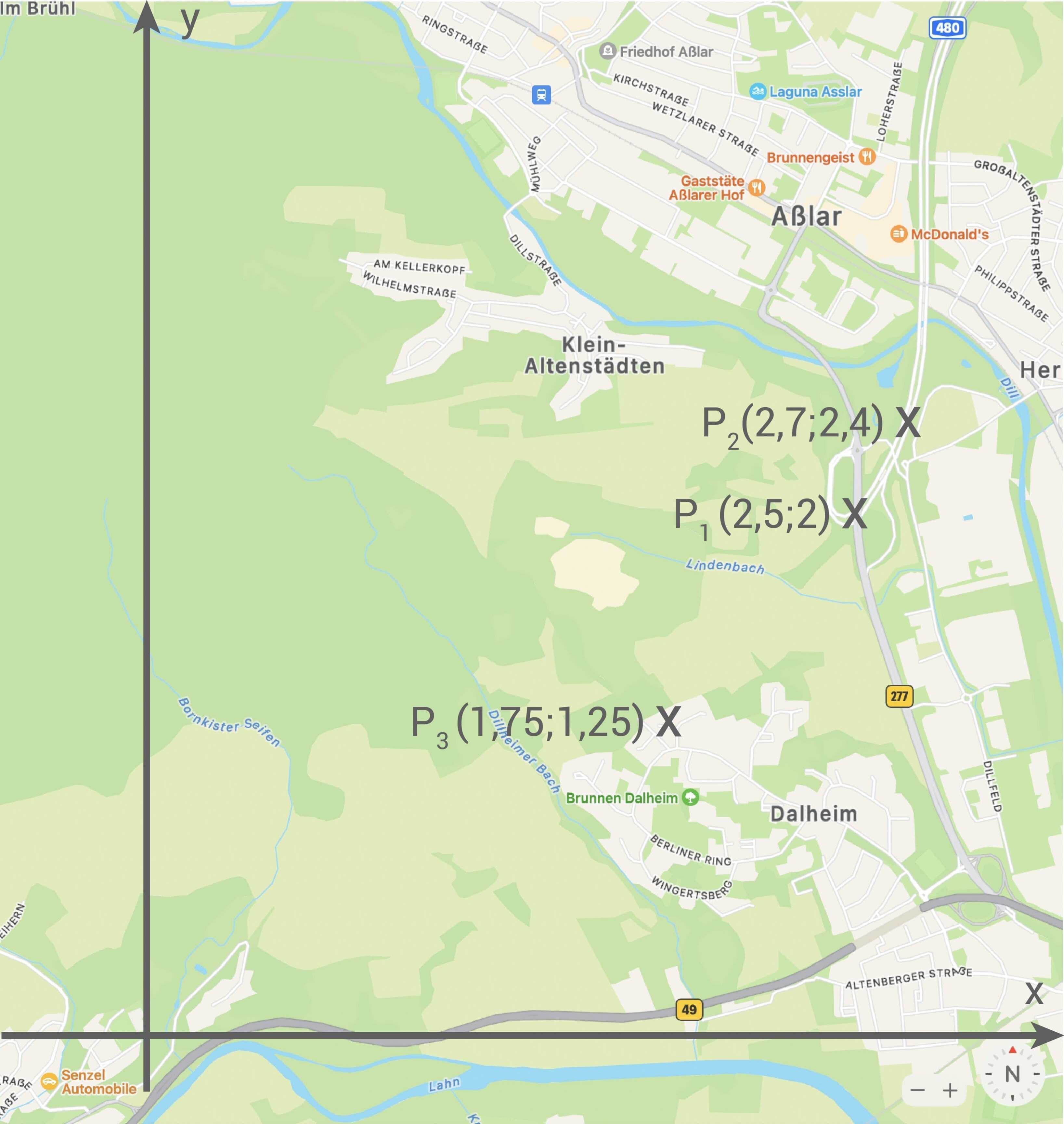
Eine Umgehungsstraße in der Nähe der Stadt Wetzlar wird geplant und soll Bundesstraßen (B49/B277) und einen Autobahnzubringer (A480) verbinden. Hierbei wird der im Material dargestellte Kartenausschnitt verwendet, wobei die $y$ -Achse Richtung Norden zeigt und eine Einheit einem Kilometer entspricht.
Im Modell kann für $x \leq 0$ die vorhandene Bundesstraße (B49) durch den Graphen der Funktion $p$ mit $p ( x )=- x ^2+0,7 x$ beschrieben werden.
Die geplante Umgehungsstraße besteht aus zwei Abschnitten. Der erste Abschnitt, der im Modell vom Koordinatenursprung zum Anschlusspunkt $P_1(2,5 \mid 2)$ verläuft, kann durch einen Ausschnitt aus dem Graphen einer ganzrationalen Funktion dritten Grades beschrieben werden. Der zweite Abschnitt soll vom Anschlusspunkt $P_1$ bis zum Punkt $P_2(2,7 \mid 2,4)$ geradlinig verlaufen. Der Übergang der vorhandenen Bundesstraße zum ersten Abschnitt der Umgehungsstraße sowie der Übergang der beiden Abschnitte der Umgehungsstraße sollen jeweils knickfrei verlaufen.

Material
Kartenausschnitt

he mathe abi gk cas 2022 kartenausschnitt

1.1

Zeige, dass die Funktion $f$ mit $f(x)=0,176 x^3-0,4 x^2+0,7 x$ als Modellfunktion für den ersten Abschnitt der geplanten Umgehungsstraße die genannten Bedingungen für den Verlauf der Umgehungsstraße erfüllt.

(6 BE)

1.2

Untersuche, ob bei Verwendung der Modellfunktion $f$ aus Aufgabe 1.1 der erste Abschnitt der Umgehungsstraße ohne Krümmungsänderung im Anschlusspunkt $P_1(2,5 \mid 2)$ an den zweiten Abschnitt angeschlossen werden kann.

(3 BE)

Die Länge $L$ einer Kurve, die durch den Graphen einer Funktion $f$ im Intervall von $a$ bis $b$ beschrieben wird, kann mithilfe der Formel $L=\int_{a}^{b} \sqrt{1+\left[f^{\prime}(x)\right]^2} dx$ berechnet werden.

2.1

Ermittle unter Verwendung der Funktion $f$ aus Aufgabe 1.1 mit dieser Formel die Länge $L$ des ersten Abschnitts der Umgehungsstraße vom Koordinatenursprung zum Anschlusspunkt $P_1(2,5 \mid 2)$ und gib dein Ergebnis gerundet auf eine Nachkommastelle in Meter an.
(Das Höhenprofil der Landschaft soll nicht berücksichtigt werden, es kann also von einem ebenen Verlauf der Umgehungsstraße ausgegangen werden.)
Bestimme, um wie viel Prozent der erste Abschnitt der Umgehungsstraße länger ist als die geradlinige Verbindung vom Koordinatenursprung zum Punkt $P_1$ .
[Zur Kontrolle: Die Länge $L$ beträgt etwa $3,3$ Kilometer.]

(6 BE)

2.2

Die Oberfläche der im ersten Abschnitt $24 \,\text{m}$ breiten Umgehungsstraße soll mit einer $4 \,\text{cm}$ starken Deckschicht asphaltiert werden. Erkläre die folgende Formel zur Bestimmung des Volumens dieser Deckschicht des ersten Abschnitts der geplanten Umgehungsstraße auf einem Intervall $[a;b].$
$V ( a ; b )=\left(\int_{ a }^{ b } \sqrt{1+\left( f ^{\prime}( x )\right)^2} dx \right) \cdot$ $0,024 \cdot 0,00004$
Gib unter Verwendung der Funktion $f$ aus Aufgabe 1.1 das Volumen der Deckschicht des ersten Abschnitts der Umgehungsstraße vom Koordinatenursprung zur Anschlussstelle $P_1(2,5 \mid 2)$ in Kubikmeter an.

(5 BE)

2.3

Die gesamte Umgehungsstraße soll $3,75 \,\text{km}$ lang werden. Es wird ein Durchschnittsverbrauch von 7,5 Liter Treibstoff pro $100 \,\text{km}$ gemittelt über alle Fahrzeuge angenommen. Für die Menge an $CO_2$ , die pro Fahrzeug ausgestoßen wird, werden $2,4 \,\text{kg}$ pro Liter Treibstoff angenommen. Es wird davon ausgegangen, dass pro Tag $10.000$ Fahrzeuge mit Verbrennungsmotor die Umgehungsstraße nutzen.
Berechne unter den genannten Voraussetzungen die Menge an $CO_2$ in Tonnen, die pro Jahr durch die Fahrzeuge auf der Umgehungsstraße ausgestoßen wird.

(4 BE)

Gegeben ist die Funktionenschar $f_{ t }$ mit

Funktionenschar anzeigen

3.1

Zeige rechnerisch, dass man für den Wert $t=2$ die Funktionsgleichung der Funktion $f$ aus Aufgabe 1.1 erhält.

(2 BE)

3.2

Falls die geplante Umgehungsstraße südlich des Punkts $P_3(1,75 \mid 1,25)$ verläuft, in der Abbildung im Material also zwischen $P_3$ und der $x$ -Achse, kommt die Umgehungsstraße einem Wohngebiet zu nah oder durchquert es sogar, sodass eine Änderung des Straßenverlaufs notwendig wird.
Bestätige, dass dies bei Verwendung der Funktion $f _2$ der Fall ist.
Bestimme den Wert für den Parameter $t$ , für welchen der Graph der zugehörigen Funktion der Schar durch den Punkt $P_3$ verläuft.

(5 BE)

3.3

Ermittle allgemein die Steigung der Graphen der Funktionenschar $f_t$ im Punkt $P_1$ . Es soll diejenige Funktion der Schar $f_t$ als Modellfunktion für den ersten Abschnitt der Umgehungsstraße verwendet werden, deren Graph durch den Punkt $P_3$ verläuft.
Prüfe, ob am Anschlusspunkt $P_1$ der Übergang zum zweiten Abschnitt der Umgehungsstraße weiterhin knickfrei verläuft.

(5 BE)

3.4

Bestimme alle Werte des Parameters $t$ , für welche bei Verwendung von Funktionen der Schar $f_t$ als Modellfunktionen für den ersten Abschnitt der Umgehungsstraße die Umgehungsstraße im Anschlusspunkt $P_1$ linksgekrümmt ist.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Voraussetzungen für den ersten Abschnitt der Umgehungsstraße sind, dass diese durch eine ganzrationale Funktion dritten Grades beschrieben wird und die Übergänge bei $x=0$ zur Bundesstraße und bei $x=2,5$ zum zweiten Abschnitt der Umgehungsstraße knickfrei verlaufen.

1. Schritt: Punkte $O(0 \mid 0)$ und $P_1(2,5 \mid 2)$ prüfen

Damit die Straßen knickfrei ineinander verlaufen können, muss der Graph von $f$ die Punkte $O(0 \mid 0)$ und $P_1(2,5 \mid 2)$ beinhalten.

$\begin{array}[t]{rll} f(0)&=& 0,176\cdot 0^3-0,4\cdot 0^2+0,7\cdot 0 &\\[5pt] &=& 0 \end{array}$

$\begin{array}[t]{rll} f(2,5)&=&0,176\cdot 2,5^3-0,4\cdot 2,5^2+0,7\cdot 2,5 & \\[5pt] &=& 2 \end{array}$

Der Graph von $f$ verläuft folglich durch die beiden Anschlusspunkte.

2. Schritt: Übergang bei $x=0$ prüfen

Die Funktionen $p(x)$ und $f(x)$ gehen genau dann knickfrei ineinander über, wenn die Werte der Ableitungen an der Stelle $x=0$ identisch sind.

$\(\begin{array}[t]{rll} p$

$\(\begin{array}[t]{rll} f$

Da $\(p$ gilt, gehen die beiden Straßen bei $x=0$ knickfrei ineinander über.

3. Schritt: Übergang bei $x=2,5$ prüfen

Steigung $m$ des geradlinig verlaufenden zweiten Abschnitts der Umgehungsstraße berechnen:

$m=\dfrac{2,4-2}{2,7-2,5}=\dfrac{0,4}{0,2}=2$

Rechenweg anzeigen

Da $\(m=f$ gilt, gehen die beiden Abschnitte der Umgehungsstraße an der Stelle $x=2,5$ knickfrei ineinander über.

Die Funktion $f$ erfüllt somit als Modellfunktion die Bedingungen für den Verlauf der Umgehungsstraße.

1.2

Eine Krümmungsänderung findet an den Wendepunkten des Graphen statt.

Notwendige Bedingung für Wendestellen anwenden

$\(\begin{array}[t]{rll} f$

Die notwendige Bedingung ist ausreichend: Da die Stelle $x=2,5$ keine Wendestelle des Graphen ist, kann die Umgehungsstraße im Punkt $P_1$ ohne Krümmungsänderung angeschlossen werden.

2.1

Länge des ersten Abschnitts ermitteln

Rechenweg anzeigen

Mit dem CAS ergibt sich: $L\approx 3,3$

Prozentuale Abweichung bestimmen

Länge der geradlinigen Verbindung berechnen:

$\begin{array}[t]{rll} |\overrightarrow{OP_1}|&=&\sqrt{(2,5)^2+(2)^2} & \\[5pt] &\approx& 3,2 \end{array}$

$\begin{array}[t]{rll} p&=& \dfrac{100\,\%\cdot 3,3}{3,2} &\approx& 104,1\,\% \end{array}$

Der erste Abschnitt der Umgehungsstraße ist folglich etwa $4\,\%$ länger als die geradlinige Verbindung vom Koordinatenursprung zum Punkt $P_1$

2.2

Formel erklären

Das Volumen $V$ der Deckschicht wird in $\,\text{km}^3$ berechnet. Es wird die Länge $L$ der Strecke, welche mit der vorgegeben Formel berechnet werden kann, mit der Breite und Höhe der Deckschicht in der Einheit $\,\text{km}$ multipliziert.

Volumen berechnen

$\begin{array}[t]{rll} V(0;2,5)&=& 3,3\cdot 0,024 \cdot 0,00004 & \\[5pt] &=& 0,00000317 [\,\text{km}^3]& \\[5pt] &=& 3170 [\,\text{m}^3] \end{array}$

2.3