C - Stochastik
1
1.1
Bestimme unter Angabe einer geeigneten Zufallsgröße für folgende Ereignisse jeweils die Wahrscheinlichkeit:
„Unter den ausgewählten Pkw sind genau acht Dieselfahrzeuge.“
„Unter den ausgewählten Pkw sind mindestens fünf Dieselfahrzeuge.“
(3 BE)
1.2
Von den 25 ausgewählten Pkw sind genau fünf Dieselfahrzeuge.
Bestimme die Wahrscheinlichkeit dafür, dass die drei roten Pkw Dieselfahrzeuge sind.
(3 BE)
1.3
Berechne, wie groß die Anzahl zufällig ausgewählter Pkw des Herstellers mindestens sein muss, damit die Wahrscheinlichkeit dafür, dass unter diesen mindestens ein Dieselfahrzeug ist, mindestens 
beträgt.
(5 BE)
2
2.1
Stelle den Sachverhalt in einem beschrifteten Baumdiagramm dar.
(3 BE)
2.2
Berechne die Wahrscheinlichkeit dafür, dass die Leistung eines zufällig ausgewählten Pkw des Herstellers größer als 
ist.
Bestimme die Wahrscheinlichkeit dafür, dass es sich bei einem zufällig ausgewählten Pkw des Herstellers mit einer Leistung von mehr als um ein Dieselfahrzeug handelt.
(4 BE)
3
In einem Werk des Pkw-Herstellers aus Aufgabe 1 produziert eine Maschine Ersatzteile. Durch einen Fehler in der Einstellung produzierte die Maschine einen Ausschussanteil (Anteil an unbrauchbaren Teilen) von mindestens 
Die Maschine wurde daraufhin gewartet und neu eingestellt.
Es soll mit Hilfe eines geeigneten Hypothesentests überprüft werden, ob sich der Ausschussanteil der Maschine verringert hat. Dazu werden der Produktion zufällig 100 Ersatzteile entnommen. Die Anzahl der unbrauchbaren Teile in einer Stichprobe soll modellhaft als binomialverteilt angenommen werden.
Begründe, dass es sich um einen linksseitigen Hypothesentest handelt.
Entwickle einen entsprechenden Test auf einem Signifikanzniveau von 
und formuliere eine Entscheidungsregel im Sachzusammenhang.
(6 BE)
4
Betrachtet werden binomialverteilte Zufallsgrößen, die für eine Trefferwahrscheinlichkeit 
mit 
die Anzahl der Treffer bei 
Versuchen angeben.
Die Standardabweichung der Zufallsgrößen ist 3.
4.1
Bestimme für eine Zufallsgröße mit einer Trefferwahrscheinlichkeit von 
die zugehörige Anzahl der Versuche.
(3 BE)
4.2
Zeige, dass es keinen Wert für geben kann, für den die Anzahl der Versuche 9 ist.
Binomialsummenfunktion:
(3 BE)
1.1
Zufallsgröße angeben
Die Zufallsgröße 
beschreibt die Anzahl der Dieselfahrzeuge von 25 zufällig ausgewählten Fahrzeugen.
X ist binomialverteilt mit 
und 
Wahrscheinlichkeiten bestimmen
Mit einer Wahrscheinlichkeit von ca. 
befinden sich unter den ausgewählten Fahrzeugen genau acht Dieselfahrzeuge.
Mit einer Wahrscheinlichkeit von 
befinden sich unter den ausgewählten Pkw mindestens fünf Dieselfahrzeuge.
Mit dem binomPDf-Befehl des CAS folgt:
![\(\begin{array}[t]{rll}
P(A)&=& P(X=8)& \quad \scriptsize \mid CAS \\[5pt]
&\approx& 0,0623 & \\[5pt]
&=& 6,23 \,\%
\end{array}\)](https://mathjax.schullv.de/31df5517fa423ae241692896feac6b7cc2fb0008ee448e9abaa3da5ca5dd98b3?color=5a5a5a)
Mit dem binomCDf-Befehl des CAS folgt weiter:
![\(\begin{array}[t]{rll}
P(B)&=& P(X \geq 5)& \\[5pt]
&=& P (5 \leq X \leq 25) &\quad \scriptsize \mid\; CAS \\[5pt]
&=& 0,5793 & \\[5pt]
&=& 57,93 \,\%
\end{array}\)](https://mathjax.schullv.de/11b1d257b0ec968c9c2c2385e2ffd9fd169f09457af1819b5c67d3471218a8b0?color=5a5a5a)
1.2
1.3
Die Zufallsgröße 
beschreibt die Anzahl der Dieselfahrzeuge unter zufällig ausgewählten Fahrzeugen und ist binomialverteilt mit unbekanntem und
Es soll gelten:
![\(\begin{array}[t]{rll}
P(X_n\geq 1)&\geq& 0,95\\[5pt]
1- P(X_n =0)&\geq& 0,95 \\[5pt]
1- \dbinom{n}{0}\cdot 0,2^0 \cdot 0,8^n&\geq& 0,95 &\quad \scriptsize \mid\; CAS \\[5pt]
n&\geq & 13,43 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/3d3573571847018a4f0646a7e87caacfc1c79f3d9f1cfbce65920b65a13232e4?color=5a5a5a)
Es müssen somit mindestens 14 Pkw ausgewählt werden, damit sich mit einer Wahrscheinlichkeit von mindestens 
mindestens ein Dieselfahrzeug darunter befindet.
2.1
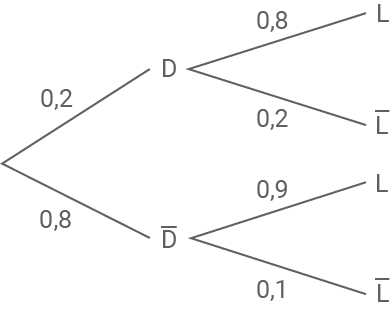
2.2
Mit Hilfe des Baumdiagrammes aus Aufgabe 2.1 und den Pfadregeln ergibt sich:
![\(\begin{array}[t]{rll}
P(L)&=& 0,2\cdot 0,8 + 0,8\cdot 0,9 \\[5pt]
&=& 0,88 \\[5pt]
&=& 88\,\% \\[5pt]
\end{array}\)](https://mathjax.schullv.de/d1f42ce6385f15acf9f4ef5318ef9bbc5f507413dfac94539d723d05dfe0b358?color=5a5a5a)
Mit einer Wahrscheinlichkeit von 
hat ein zufällig ausgewähltes Dieselfahrzeug also eine Leistung von mehr als 
Mit dem Satz von Bayes folgt:
![\(\begin{array}[t]{rll}
P_L(D)&=& \dfrac{P(D \cap L) }{P(L)} \\[5pt]
&=& \dfrac{0,8\cdot 0,2}{0,88} \\[5pt]
&\approx& 0,1818\\[5pt]
&=& 18,18\,\% \\[5pt]
\end{array}\)](https://mathjax.schullv.de/0f27703a9239fece3807f27e3297e2b6b51f13cb60ae6be0f529bc458c7ff8d5?color=5a5a5a)
Mit einer Wahrscheinlichkeit von ca. 
handelt es sich bei einem Pkw mit einer höheren Leistung als 
um ein Dieselfahrzeug.
3
Begründung
Mit dem Hypothesentest soll überprüft werden, ob sich der Ausschussanteil der Maschine verringert hat, das heißt die Vermutung 
soll bestätigt werden.
Die Nullhypothese lautet also:
Somit handelt es sich um einen linksseitigen Hypothesentest.
Test entwickeln
Die Zufallsgröße 
beschreibt die Anzahl der Ersatzteile aus der Stichprobe, die Ausschuss sind.
soll gemäß der Nullhypothese verteilt sein und kann als binomialverteilt mit den Parametern 
und 
angenommen werden.
Da auf einem Signifikanzniveau von 
getestet werden soll, muss gelten:
Mit Hilfe der Tabelle aus den Aufgaben folgt:
Mit 
ergibt sich die Entscheidungsregel:
Wenn höchstens 2 der entnommenen Ersatzteile Ausschuss sind, geht man davon aus, dass die Wartung erfolgreich war und sich der Ausschussanteil verringert hat.
4.1
Einsetzen von 
und 
in die Gleichung für die Standardabweichung liefert:
![\(\begin{array}[t]{rll}
\sigma&=&\sqrt{n\cdot p\cdot (1-p)} \\[5pt]
3&=& \sqrt{n\cdot 0,25\cdot 0,75} \\[5pt]
3&=&\sqrt{n\cdot 0,1875} &\quad \scriptsize \mid\;(\,)^2 \\[5pt]
9&=&n\cdot 0,1875 &\quad \scriptsize \mid\; : 0,1875\\[5pt]
48&=& n
\end{array}\)](https://mathjax.schullv.de/c5878240a71d5d6d7ab3aebeddae2381f7384668d0a87bdccb018df31d40f8d3?color=5a5a5a)
Es müssen folglich 48 Versuche durchgeführt werden.
4.2
Einsetzen der Werte 
und in die Gleichung der Standardabweichung liefert:
![\(\begin{array}[t]{rll}
3&=&\sqrt{9\cdot p\cdot(1-p)} &\quad \scriptsize \mid\; (\,)^2\\[5pt]
9&=&9\cdot p \cdot (1-p) &\quad \scriptsize \mid\; :9 \\[5pt]
1&=&p\cdot(1-p) \\[5pt]
1&=&p-p^2 &\quad \scriptsize \mid\; -1\\[5pt]
0&=&p-p^2-1 &\quad \scriptsize \mid\; \cdot (-1)\\[5pt]
0&=&p^2-p+1
\end{array}\)](https://mathjax.schullv.de/ded42c348a4267d9862d51c7942c980965bec0ad87a3ea5040d604a548ba79c5?color=5a5a5a)
Mit der 
-Formel ergibt sich:
![\(\begin{array}[t]{rll}
p_{1,2}&=& -\dfrac{-1}{2} \pm \sqrt{\left(\dfrac{-1}{2}\right)^2-1} \\[5pt]
&=& \dfrac{1}{2}\pm \sqrt{-\dfrac{3}{4}} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/940ec51392ba40582683387afeaaec2f74add6caf9c42782c4f0c6cbddf4a620?color=5a5a5a)
Da unter der Wurzel ein negativer Audruck steht, hat diese Gleichung keine Lösung.
Es gibt also keinen Wert von 
für den die Anzahl der Versuche 9 beträgt.
1.1
Zufallsgröße angeben
Die Zufallsgröße beschreibt die Anzahl der Dieselfahrzeuge von 25 zufällig ausgewählten Fahrzeugen.
X ist binomialverteilt mit und
Wahrscheinlichkeiten bestimmen
Mit einer Wahrscheinlichkeit von ca. befinden sich unter den ausgewählten Fahrzeugen genau acht Dieselfahrzeuge.
Mit einer Wahrscheinlichkeit von befinden sich unter den ausgewählten Pkw mindestens fünf Dieselfahrzeuge.
Mit dem binomPDf-Befehl des CAS folgt:
Mit dem binomCDf-Befehl des CAS folgt weiter:
1.2
1.3
Die Zufallsgröße beschreibt die Anzahl der Dieselfahrzeuge unter zufällig ausgewählten Fahrzeugen und ist binomialverteilt mit unbekanntem und
Es soll gelten:
Es müssen somit mindestens 14 Pkw ausgewählt werden, damit sich mit einer Wahrscheinlichkeit von mindestens mindestens ein Dieselfahrzeug darunter befindet.
2.1
2.2
Mit Hilfe des Baumdiagrammes aus Aufgabe 2.1 und den Pfadregeln ergibt sich:
Mit einer Wahrscheinlichkeit von hat ein zufällig ausgewähltes Dieselfahrzeug also eine Leistung von mehr als
Mit dem Satz von Bayes folgt:
Mit einer Wahrscheinlichkeit von ca. handelt es sich bei einem Pkw mit einer höheren Leistung als um ein Dieselfahrzeug.
3
Begründung
Mit dem Hypothesentest soll überprüft werden, ob sich der Ausschussanteil der Maschine verringert hat, das heißt die Vermutung soll bestätigt werden.
Die Nullhypothese lautet also:
Somit handelt es sich um einen linksseitigen Hypothesentest.
Test entwickeln
Die Zufallsgröße beschreibt die Anzahl der Ersatzteile aus der Stichprobe, die Ausschuss sind.
soll gemäß der Nullhypothese verteilt sein und kann als binomialverteilt mit den Parametern und angenommen werden.
Da auf einem Signifikanzniveau von getestet werden soll, muss gelten:
Mit Hilfe der Tabelle aus den Aufgaben folgt:
Mit ergibt sich die Entscheidungsregel:
Wenn höchstens 2 der entnommenen Ersatzteile Ausschuss sind, geht man davon aus, dass die Wartung erfolgreich war und sich der Ausschussanteil verringert hat.
4.1
Einsetzen von und in die Gleichung für die Standardabweichung liefert:
Es müssen folglich 48 Versuche durchgeführt werden.
4.2
Einsetzen der Werte und in die Gleichung der Standardabweichung liefert:
Mit der -Formel ergibt sich:
Da unter der Wurzel ein negativer Audruck steht, hat diese Gleichung keine Lösung.
Es gibt also keinen Wert von für den die Anzahl der Versuche 9 beträgt.