C2.1 - Stochastik
1
In einem großen Unternehmen werden Elektronikgeräte hergestellt. Erfahrungsgemäß sind  der hergestellten Geräte defekt.
der hergestellten Geräte defekt.
1.1
Bestimme die Wahrscheinlichkeiten der folgenden Ereignisse.
 Von 500 zufällig ausgewählten Geräten sind genau 10 defekt.
Von 500 zufällig ausgewählten Geräten sind genau 10 defekt.
 Von 750 zufällig ausgewählten Geräten sind maximal 25 defekt.
Von 750 zufällig ausgewählten Geräten sind maximal 25 defekt.
 Von 400 zufällig ausgewählten Geräten funktionieren mindestens 381 einwandfrei.
Von 400 zufällig ausgewählten Geräten funktionieren mindestens 381 einwandfrei.
(6 BE)
1.2
1.3
Berechne die Anzahl der Geräte, die man mindestens überprüfen muss, um mit einer Wahrscheinlichkeit von mindestens  mindestens ein defektes Gerät zu erhalten.
mindestens ein defektes Gerät zu erhalten.
(4 BE)
1.4
Es werden 300 zufällig ausgewählte Geräte getestet.
Berechne den Erwartungswert für die Anzahl der defekten Geräte.
(2 BE)
1.5
Das Unternehmen hat ein neues Bauteil entwickelt, das in viele Elektronikgeräte eingebaut wurde. Es wird vermutet, dass sich dadurch der Anteil der defekten Geräte verringert hat.
Zur Überprüfung dieser Vermutung werden 300 zufällig ausgewählte Geräte auf ihre Funktionstüchtigkeit getestet.
Entwickle einen linksseitigen Hypothesentest auf einem Signifikanzniveau von  Formuliere eine Entscheidungsregel im Sachzusammenhang.
Formuliere eine Entscheidungsregel im Sachzusammenhang.
(6 BE)
2
In einem großen Unternehmen sind  aller Beschäftigten mit der Höhe ihres Gehalts zufrieden.
aller Beschäftigten mit der Höhe ihres Gehalts zufrieden.  aller Beschäftigten sind in der Werbeabteilung tätig und nicht zufrieden mit der Höhe ihres Gehalts. Insgesamt gehören der Werbeabteilung
aller Beschäftigten sind in der Werbeabteilung tätig und nicht zufrieden mit der Höhe ihres Gehalts. Insgesamt gehören der Werbeabteilung  aller Beschäftigten an.
aller Beschäftigten an.
 aller Beschäftigten die Frage
aller Beschäftigten die Frage  zugeteilt, den übrigen Beschäftigten die folgende Frage
zugeteilt, den übrigen Beschäftigten die folgende Frage 
 "Beabsichtigen Sie, das Unternehmen innerhalb der nächsten zwölf Monate zu verlassen?"
"Beabsichtigen Sie, das Unternehmen innerhalb der nächsten zwölf Monate zu verlassen?"
 "Beabsichtigen Sie, für die nächsten zwölf Monate im Unternehmen zu bleiben?"
Nur der befragten Person selbst ist bekannt, welche Frage ihr zugeteilt wurde. Die befragte Person beantwortet die Frage wahrheitsgemäß.
Das folgende Baumdiagramm stellt einen Teil des beschriebenen Verfahrens dar.
"Beabsichtigen Sie, für die nächsten zwölf Monate im Unternehmen zu bleiben?"
Nur der befragten Person selbst ist bekannt, welche Frage ihr zugeteilt wurde. Die befragte Person beantwortet die Frage wahrheitsgemäß.
Das folgende Baumdiagramm stellt einen Teil des beschriebenen Verfahrens dar.
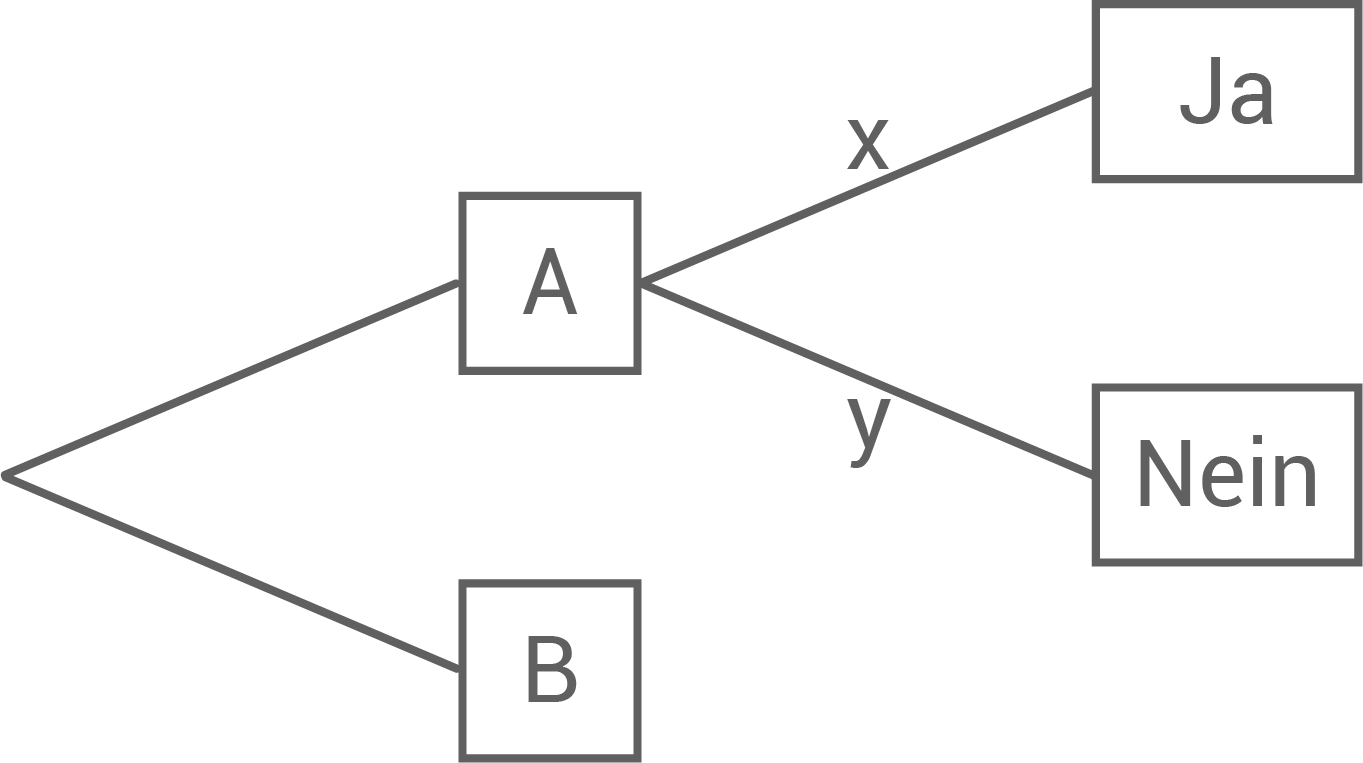
 zugeteilt wurde, ebenso groß ist wie unter denjenigen, denen die Frage
zugeteilt wurde, ebenso groß ist wie unter denjenigen, denen die Frage  zugeteilt wurde.
zugeteilt wurde.
2.1
Stelle den Sachzusammenhang in einer vollständig ausgefüllten Vierfeldertafel dar.
(3 BE)
2.2
Untersuche, ob der Anteil der Beschäftigten, die mit ihrem Gehalt nicht zufrieden sind, in der Werbeabteilung größer ist als im übrigen Unternehmen.
(3 BE)
2.3
Bestimme die Wahrscheinlichkeit dafür, dass sich unter 500 zufällig ausgewählten Beschäftigten mehr als 400 Beschäftigte befinden, die mit ihrem Gehalt zufrieden sind.
(2 BE)
2.4
Beschreibe die Bedeutung des Terms  im Sachzusammenhang.
im Sachzusammenhang.
Im Rahmen der Befragung soll ermittelt werden, wie viele Beschäftigte beabsichtigen, das Unternehmen innerhalb der nächsten zwölf Monate zu verlassen. Um zu vermeiden, dass Befragte aus Sorge vor negativer Konsequenzen nicht wahrheitsgemäß antworten, wird ein besonderes Verfahren angewendet. Dabei wird
(3 BE)

2.5
Gib die Bedeutung von  im Sachzusammenhang an.
im Sachzusammenhang an.
Von den 2700 Beschäftigten antworten 1024 mit "Ja". Es kann davon ausgegangen werden, dass der Anteil der Beschäftigten mit der Absicht, das Unternehmen innerhalb der nächsten zwölf Monate zu verlassen, unter denjenigen, denen die Frage
(2 BE)
2.6
Zeige, dass aufgrund des Ergebnisses der Befragung davon auszugehen ist, dass etwa  der Beschäftigten beabsichtigen, das Unternehmen innerhalb der nächsten zwölf Monate zu verlassen.
der Beschäftigten beabsichtigen, das Unternehmen innerhalb der nächsten zwölf Monate zu verlassen.
(4 BE)
2.7
Eine beschäftigte Person, die mit "Ja" geantwortet hat, wird zufällig ausgewählt. Ermittle die Wahrscheinlichkeit dafür, dass diese Person beabsichtigt, das Unternehmen innerhalb der nächsten zwölf Monate zu verlassen.
(3 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
1.1
1.2
Durch aufteilen von  in die einzelnen Summanden lassen sich diese separat untersuchen:
Aus der Formel der Wahrscheinlichkeit eines binomialverteilten Ereignis lassen sich
in die einzelnen Summanden lassen sich diese separat untersuchen:
Aus der Formel der Wahrscheinlichkeit eines binomialverteilten Ereignis lassen sich  ,
,  ,
,  direkt aus den Summanden entnehmen:
direkt aus den Summanden entnehmen:
 Bezogen auf den Sachverhalt entspricht dies der Wahrscheinlichkeit: Von 100 zufällig ausgewählten Geräten sind genau 3 defekt.
Bezogen auf den Sachverhalt entspricht dies der Wahrscheinlichkeit: Von 100 zufällig ausgewählten Geräten sind genau 3 defekt.
 Bezogen auf den Sachverhalt entspricht dies der Wahrscheinlichkeit: Von 100 zufällig ausgewählten Geräten sind genau 4 defekt.
Bezogen auf den Sachverhalt entspricht dies der Wahrscheinlichkeit: Von 100 zufällig ausgewählten Geräten sind genau 4 defekt.
 Bezogen auf den Sachverhalt entspricht dies der Wahrscheinlichkeit: Von 100 zufällig ausgewählten Geräten sind genau 5 defekt.
Insgesamt lässt sich Ereignis
Bezogen auf den Sachverhalt entspricht dies der Wahrscheinlichkeit: Von 100 zufällig ausgewählten Geräten sind genau 5 defekt.
Insgesamt lässt sich Ereignis  also wie folgt beschreiben:
also wie folgt beschreiben:
 Von 100 zufällig ausgewählten Geräten sind genau 3, 4 oder 5 Geräte defekt.
Von 100 zufällig ausgewählten Geräten sind genau 3, 4 oder 5 Geräte defekt.
1.3
Die Zufallsvariable  beschreibt die Anzahl defekter Geräte und ist
beschreibt die Anzahl defekter Geräte und ist  verteilt.
Gesucht ist das kleinste
verteilt.
Gesucht ist das kleinste  , für das gilt:
, für das gilt:
![\(\begin{array}[t]{rll}
P(X \geq 1)& \geq& 0,99& \quad \scriptsize \\[5pt]
P(X = 0)& \leq& 0,01& \quad \scriptsize \\[5pt]
(1 - 0,03)^n& \leq& 0,01 \quad \scriptsize \\[5pt]
0,97^n& \leq& 0,01& \quad \scriptsize \\[5pt]
n& \geq & \dfrac{\ln(0,01)}{\ln(0,97)} \\[5pt]
n& \geq & 151,19
\end{array}\)](https://mathjax.schullv.de/02bf0c63f01e8f2212ea1daa61ab3ff212defc13e607bc6f14de7851fb2f5ce1?color=5a5a5a) Somit müssen mindestens 152 Geräte überprüft werden, um mit einer Wahrscheinlichkeit von mindestens
Somit müssen mindestens 152 Geräte überprüft werden, um mit einer Wahrscheinlichkeit von mindestens  mindestens ein defektes Gerät zu erhalten.
mindestens ein defektes Gerät zu erhalten.
1.4
Die Zufallsvariable  beschreibt die Anzahl defekter Geräte und ist
beschreibt die Anzahl defekter Geräte und ist  verteilt.
Für den Erwartungswert gilt:
verteilt.
Für den Erwartungswert gilt:
 Damit beträgt der Erwartungswert für die Anzahl defekter Geräte
Damit beträgt der Erwartungswert für die Anzahl defekter Geräte 
1.5
Aus der Aufgabenstellung geht hervor:

 Die Zufallsvariable
Die Zufallsvariable  beschreibt die Anzahl defekter Geräte und ist
beschreibt die Anzahl defekter Geräte und ist  verteilt.
Gesucht wird die größte natürliche Zahl
verteilt.
Gesucht wird die größte natürliche Zahl  , sodass gilt:
, sodass gilt:
 Durch systematisches Ausprobieren mit dem WTR folgt:
Durch systematisches Ausprobieren mit dem WTR folgt:

 Damit gilt für den Ablehnungsbereich:
Damit gilt für den Ablehnungsbereich:  Entscheidungsregel
Wenn maximal 3 Geräte nicht funktionieren, wird die Nullhypothese abgelehnt. Das neue Bauteil würde also den Anteil defekter Geräte tatsächlich verringern. Wenn 4 oder mehr Geräte defekt sind, wird die Nullhypothese nicht abgelehnt. Das neue Bauteil würde dann den Anteil defekter Geräte nicht verringern.
Entscheidungsregel
Wenn maximal 3 Geräte nicht funktionieren, wird die Nullhypothese abgelehnt. Das neue Bauteil würde also den Anteil defekter Geräte tatsächlich verringern. Wenn 4 oder mehr Geräte defekt sind, wird die Nullhypothese nicht abgelehnt. Das neue Bauteil würde dann den Anteil defekter Geräte nicht verringern.
2
2.1
| Gesamt | |||
|---|---|---|---|
| Gesamt |
2.2
Anteil unzufriedener Personen in der Werbeabteilung:
 Anteil unzufriedener Personen im gesamten Unternehmen:
Anteil unzufriedener Personen im gesamten Unternehmen:
 Damit ist der Anteil der Personen, die mit ihrem Gehalt unzufrieden sind, in der Werbeabteilung größer als im gesamten Unternehmen.
Damit ist der Anteil der Personen, die mit ihrem Gehalt unzufrieden sind, in der Werbeabteilung größer als im gesamten Unternehmen.
2.3
Die Zufallsvariable  beschreibt die Anzahl der Beschäftigten, die mit ihrem Gehalt zufrieden sind und ist
beschreibt die Anzahl der Beschäftigten, die mit ihrem Gehalt zufrieden sind und ist  verteilt.
Es gilt:
verteilt.
Es gilt:
![\(\begin{array}[t]{rll}
P(X \gt 400)&=&1 - P(X \leq 400) & \\[5pt]
&\approx& 0,048
\end{array}\)](https://mathjax.schullv.de/999a032f1ecbba128651a2bc1c72b6321eebc593d7b0395dd8101f75ae9d32ff?color=5a5a5a) Die Wahrscheinlichkeit dafür, dass unter 500 zufällig ausgewählten Beschäftigten mehr als 400 Beschäftigte mit ihrem Gehalt zufrieden sind, beträgt ungefähr
Die Wahrscheinlichkeit dafür, dass unter 500 zufällig ausgewählten Beschäftigten mehr als 400 Beschäftigte mit ihrem Gehalt zufrieden sind, beträgt ungefähr 
2.4
Der Term gibt die Wahrscheinlichkeit dafür an, dass unter 600 zufällig ausgewählten Beschäftigten nicht 400 Beschäftigte mit ihrem Gehalt unzufrieden sind und somit, dass nur 200 von 600 zufällig ausgewählten Beschäftigten mit ihrem Gehalt zufrieden sind.
2.5
2.6
Sei  der Anteil der Beschäftigten, die das Unternehmen innerhalb der nächsten 12 Monaten verlassen wollen. Dann gilt:
Es haben also ungefähr
der Anteil der Beschäftigten, die das Unternehmen innerhalb der nächsten 12 Monaten verlassen wollen. Dann gilt:
Es haben also ungefähr  der Beschäftigten vor, innerhalb der nächsten 12 Monate das Unternehmen zu verlassen.
der Beschäftigten vor, innerhalb der nächsten 12 Monate das Unternehmen zu verlassen.
2.7
Die Wahrscheinlichkeit, dass die befragte Person beabsichtigt, das Unternehmen innerhalb von 12 Monaten zu verlassen, beträgt ca. 