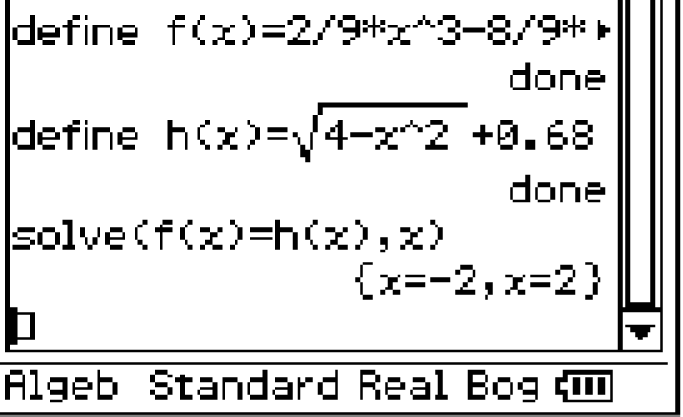A2 - Analysis
Ein Goldschmied möchte eine neue Schmuckform in seine Kollektion aufnehmen. Ein Entwurf zeigt die Designvorlage für eine Brosche.
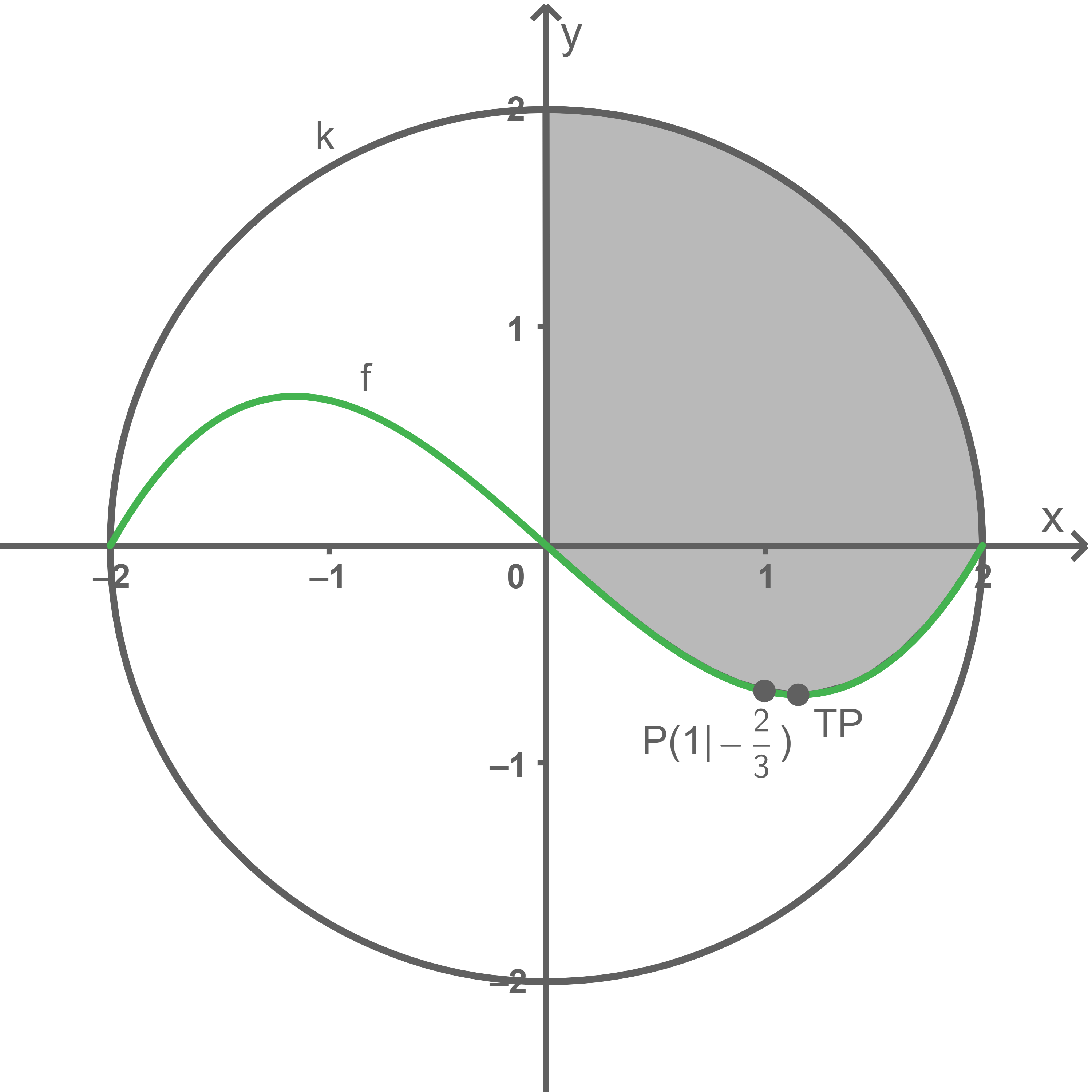
Die Trennlinie, die den Kreis in zwei gleich große Teile teilt, kann durch eine Funktion dritten Grades beschrieben werden (Angaben in Zentimetern).
1
Bestimme die Funktion  dritten Grades mit Hilfe von Abbildung 1. Erläutere deinen Ansatz.
dritten Grades mit Hilfe von Abbildung 1. Erläutere deinen Ansatz.
 zur Kontrolle:
zur Kontrolle: ![\(f(x)=\dfrac{2}{9}x^{3}-\dfrac{8}{9}x \bigg]\)](https://mathjax.schullv.de/fcc368a568320b9d4788c746e419c96ea391801556dfc55033190222fe2d3898?color=5a5a5a)
(9 BE)
2
Der grau markierte Bereich in der obigen Abbildung soll mit einer Schichtdicke von  vergoldet werden.
vergoldet werden.  der verwendeten Legierung hat eine Masse von
der verwendeten Legierung hat eine Masse von  Berechne die für eine Brosche benötigte Masse der Legierung.
Berechne die für eine Brosche benötigte Masse der Legierung.
(10 BE)
3
Bei einer zweiten Variante der Brosche wird zusätzlich zu der durch  gegebenen Linie eine zweite Linie angebracht, die durch eine Funktion
gegebenen Linie eine zweite Linie angebracht, die durch eine Funktion  mit
mit  beschrieben werden kann.
beschrieben werden kann.
3.1
Beschreibe, wie der Graph von  aus dem Graphen von
aus dem Graphen von  hervorgeht. Nimm dabei auch Bezug auf die Lage der Nullstellen und Extrempunkte.
Skizziere eine mögliche Variante in der Abbildung aus der Aufgabenstellung.
hervorgeht. Nimm dabei auch Bezug auf die Lage der Nullstellen und Extrempunkte.
Skizziere eine mögliche Variante in der Abbildung aus der Aufgabenstellung.
(5 BE)
3.2
Bestimme den Faktor  so, dass der Flächeninhalt zwischen den Graphen von
so, dass der Flächeninhalt zwischen den Graphen von  und
und  im Intervall
im Intervall ![\([-2;2]\)](https://mathjax.schullv.de/a81f3ea00c2ef2ac578efb53941c90cd2c26dc653e46e0d1b95d495a4c151746?color=5a5a5a)
 beträgt.
beträgt.
(9 BE)
4
Passend zum obigen Design soll eine stilisierte Blüte hergestellt werden.
Verschiebe die Funktion  um eine Zahl
um eine Zahl  in
in  -Richtung, so dass ihr Tiefpunkt auf der
-Richtung, so dass ihr Tiefpunkt auf der  -Achse liegt. Verschiebe
-Achse liegt. Verschiebe  mit
mit  um den gleichen Wert
um den gleichen Wert  in
in  -Richtung.
Bestimme das Volumen des Rotationskörpers, der entsteht, wenn die Fläche zwischen den verschobenen Graphen von
-Richtung.
Bestimme das Volumen des Rotationskörpers, der entsteht, wenn die Fläche zwischen den verschobenen Graphen von  und
und  im Intervall
im Intervall ![\( [-2;\;2]\)](https://mathjax.schullv.de/e7bf60993c9ef3be3c3cc33a50936babde77f2940947c3d79a71feba3e3a4311?color=5a5a5a) um die
um die  -Achse gedreht werden.
Skizziere den so entstandenen Körper.
-Achse gedreht werden.
Skizziere den so entstandenen Körper.
(9 BE)
1
Allgemeine Funktionsgleichung einer Funktion dritten Grades:
 Da die Funktion durch den Ursprung verlaufen soll, muss gelten:
Da die Funktion durch den Ursprung verlaufen soll, muss gelten:
![\(\begin{array}[t]{rll}
f(0)&=& 0 & \\[5pt]
a\cdot 0^3+b\cdot 0^2+c\cdot 0+d&=& 0& \\[5pt]
d&=& 0
\end{array}\)](https://mathjax.schullv.de/5bb5478a8ca462b8e6b94d461ac016403b6526947c5101b5d868f97d86eeff20?color=5a5a5a) Aus dem Graphen von
Aus dem Graphen von  können die Koordinaten von weiteren drei Punkten abgelesen werden. Aus diesen ergibt sich folgendes lineares Gleichungssystem:
Aus Zeile
können die Koordinaten von weiteren drei Punkten abgelesen werden. Aus diesen ergibt sich folgendes lineares Gleichungssystem:
Aus Zeile  folgt
folgt  Einsetzen in Zeile
Einsetzen in Zeile  liefert:
liefert:
![\(\begin{array}[t]{rll}
8a+4\cdot 0+2c&=& 0 &\quad \scriptsize \mid\;-8a \\[5pt]
2c&=& -8a&\quad \scriptsize \mid\; :2 \\[5pt]
c&=& -4a
\end{array}\)](https://mathjax.schullv.de/30117385b21d2fdf267cc6ee2c1aebb844cdc835cb5858d48af765a03a3b7677?color=5a5a5a) Für Zeile
Für Zeile  folgt also:
folgt also:
![\(\begin{array}[t]{rll}
a+b+c&=& -\dfrac{2}{3}& \\[5pt]
a+0-4a&=& -\dfrac{2}{3} &\\[5pt]
-3a&=& -\dfrac{2}{3} &\quad \scriptsize \mid\; :(-3) \\[5pt]
a&=& \dfrac{2}{9}
\end{array}\)](https://mathjax.schullv.de/7aa60d308e442fe1ad4c856bb7f192805fd40c611562a398535ed66513daa7a3?color=5a5a5a) Der Wert von
Der Wert von  ergibt sich nun zu
ergibt sich nun zu  Alternativ kann das lineare Gleichungssystem auch mit Hilfe des CAS durch den Befehl menu
Alternativ kann das lineare Gleichungssystem auch mit Hilfe des CAS durch den Befehl menu  3
3  3
3  1 gelöst werden.
Die Funktion
1 gelöst werden.
Die Funktion  ist somit gegeben durch:
ist somit gegeben durch:

2
1. Schritt: Flächeninhalt berechnen
Die grau markierte Fläche wird durch die  -Achse in zwei Teilflächen unterteilt:
Die Teilfläche oberhalb der
-Achse in zwei Teilflächen unterteilt:
Die Teilfläche oberhalb der  -Achse entspricht einem Viertel des Kreises. Aus der Abbildung in der Aufgabenstellung kann ein Radius von
-Achse entspricht einem Viertel des Kreises. Aus der Abbildung in der Aufgabenstellung kann ein Radius von  entnommen werden.
Mit der Formel zur Berechnung des Flächeninhalts
entnommen werden.
Mit der Formel zur Berechnung des Flächeninhalts  eines Kreises folgt also:
eines Kreises folgt also:
![\(\begin{array}[t]{rll}
A_1&=& \dfrac{1}{4}\cdot A_K & \\[5pt]
&=& \dfrac{1}{4}\cdot \pi \cdot 2^2 & \\[5pt]
&\approx& 3,14 \; [\text{cm}^2]
\end{array}\)](https://mathjax.schullv.de/d269274d49505263b33920c35cf1d8febba843582c732d70c5bf8b32f58243da?color=5a5a5a) Die Teilfläche unterhalb der
Die Teilfläche unterhalb der  -Achse entspricht der Fläche zwischen dem Graphen von
-Achse entspricht der Fläche zwischen dem Graphen von  und der
und der  -Achse im Intervall
-Achse im Intervall ![\([0;2].\)](https://mathjax.schullv.de/9f001e7a68d1db871d8f573e1477bd4c3a21c6b1fecf3e2c5b0f4e947417ade8?color=5a5a5a) Dieses Integral kann mit dem Befehl menu
Dieses Integral kann mit dem Befehl menu  4
4  3 mit dem CAS gelöst werden und ergibt
3 mit dem CAS gelöst werden und ergibt 
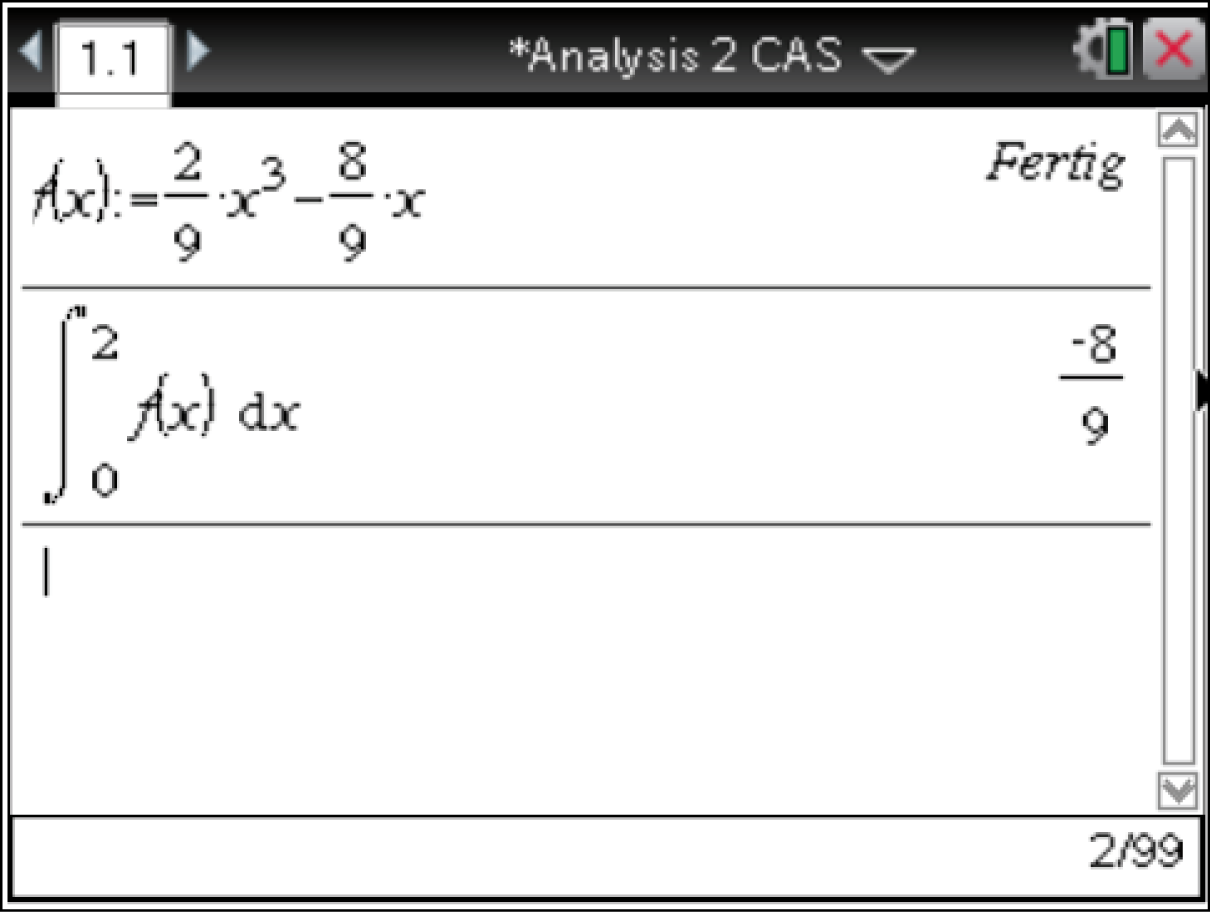 Da die Fläche unterhalb der
Da die Fläche unterhalb der  -Achse liegt und das Integral folglich negativ ist, muss der Betrag des Integrals bestimmt werden. Dieser ergibt sich demnach zu
-Achse liegt und das Integral folglich negativ ist, muss der Betrag des Integrals bestimmt werden. Dieser ergibt sich demnach zu  Der gesamte Flächeninhalt folgt also mit:
Der gesamte Flächeninhalt folgt also mit:
 2. Schritt: Volumen bestimmen
Da die Schichtdicke der Legierung
2. Schritt: Volumen bestimmen
Da die Schichtdicke der Legierung  beträgt, ergibt sich:
beträgt, ergibt sich:
 3. Schritt: Masse berechnen
Da
3. Schritt: Masse berechnen
Da  eine Masse von
eine Masse von  hat, folgt:
hat, folgt:
![\(\begin{array}[t]{rll}
m&=& 0,00403 \;\text{cm}^3 \cdot 12\dfrac{\,\text{g}}{\,\text{cm}^3}& \\[5pt]
&=& 0,04836 \,\text{g}
\end{array}\)](https://mathjax.schullv.de/a45b433c73d91ef60d835a36beca4f33c8d8ff83b5b04082eb4eb0f605745b47?color=5a5a5a) Für die Brosche wird somit eine Legierung von
Für die Brosche wird somit eine Legierung von  benötigt.
benötigt.

3.1
Verschiebung beschreiben
Der Term der Funktion  unterscheidet sich nur durch den zusätzlichen Faktor
unterscheidet sich nur durch den zusätzlichen Faktor  vom Term der Funktion
vom Term der Funktion  Mit
Mit  bewirkt dieser eine Streckung des Graphen von
bewirkt dieser eine Streckung des Graphen von  in
in  -Richtung.
Da der Funktionsgraph nicht verschoben, sondern nur gestreckt wird, bleiben die Nullstellen gleich. Auch die
-Richtung.
Da der Funktionsgraph nicht verschoben, sondern nur gestreckt wird, bleiben die Nullstellen gleich. Auch die  -Koordinate der Extrempunkte verändert sich nicht. Lediglich die
-Koordinate der Extrempunkte verändert sich nicht. Lediglich die  -Koordinate verschiebt sich in positive bzw. negative
-Koordinate verschiebt sich in positive bzw. negative  -Richtung.
Variante skizzieren
Um eine möglich Variante zu skizzieren, wird ein Wert
-Richtung.
Variante skizzieren
Um eine möglich Variante zu skizzieren, wird ein Wert  gewählt und mit dem CAS eine entsprechende Wertetabelle sowie der dazugehörige Graph der Funktion
gewählt und mit dem CAS eine entsprechende Wertetabelle sowie der dazugehörige Graph der Funktion  erstellt.
Für
erstellt.
Für  gilt beispielsweise:
gilt beispielsweise:
![\(\begin{array}[t]{rll}
g_2(x)&=& 2 \cdot f(x)& \\[5pt]
&=& 2 \cdot \left( \dfrac{2}{9} \cdot x^3 - \dfrac{8}{9} \cdot x \right)& \\[5pt]
&=& \dfrac{4}{9} \cdot x^3 - \dfrac{16}{9} \cdot x
\end{array}\)](https://mathjax.schullv.de/36a34e9fbdd620508d55b6332eeb5b328c22a0199f374af97c1debcef5f58029?color=5a5a5a) Mit dem Befehl menu
Mit dem Befehl menu  7: Tabelle ergibt sich mit dem CAS:
7: Tabelle ergibt sich mit dem CAS:
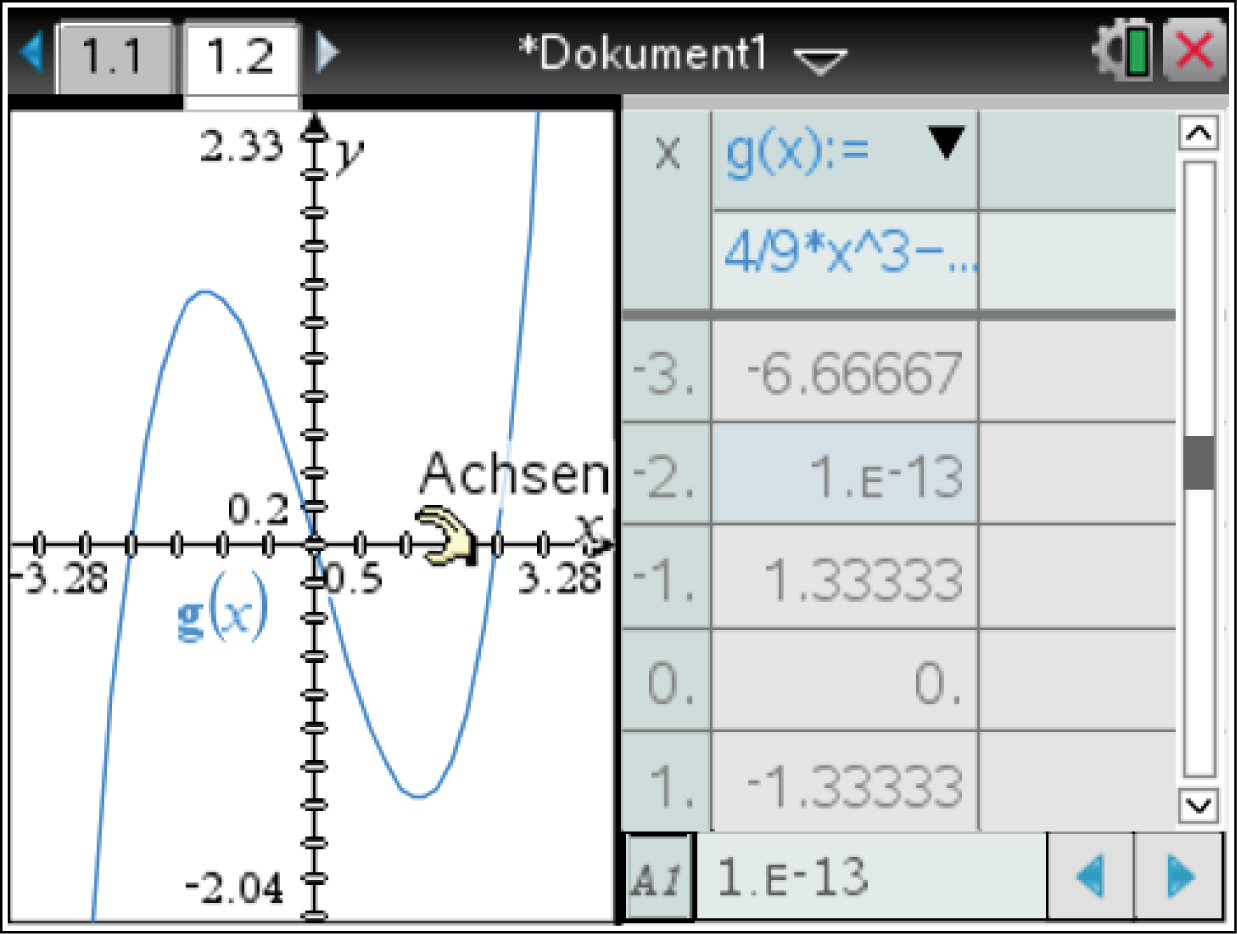 Das ergänzte Schaubild könnte also beispielsweise wie folgt aussehen:
Das ergänzte Schaubild könnte also beispielsweise wie folgt aussehen:
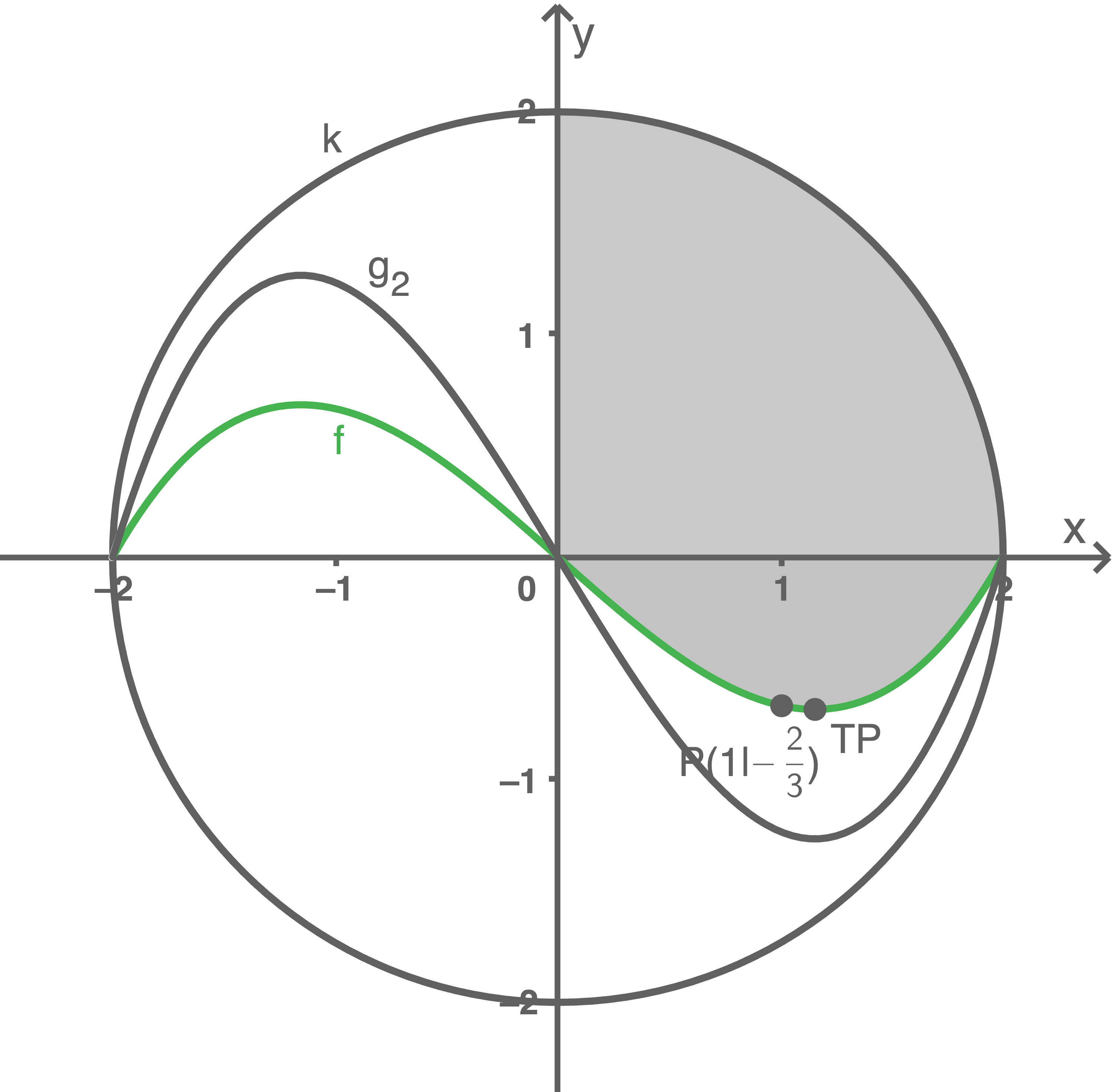


3.2
Da die beiden Funktionen  und
und  punktsymmetrisch sind, reicht es aus, die Fläche zwischen den beiden Graphen im Intervall
punktsymmetrisch sind, reicht es aus, die Fläche zwischen den beiden Graphen im Intervall ![\([-2;0]\)](https://mathjax.schullv.de/ffa38fea12f21af699510ecb456a1b88004ec0bac75ab7ac604cef40541ad9d8?color=5a5a5a) zu betrachten. Das doppelte dieser Fläche soll dann
zu betrachten. Das doppelte dieser Fläche soll dann  betragen.
Für den Flächeninhalt zwischen den Graphen von
betragen.
Für den Flächeninhalt zwischen den Graphen von  und
und  im Intervall
im Intervall ![\([-2;0]\)](https://mathjax.schullv.de/ffa38fea12f21af699510ecb456a1b88004ec0bac75ab7ac604cef40541ad9d8?color=5a5a5a) gilt:
gilt:
![\(\begin{array}[t]{rll}
A&=& 1,6 &\\[5pt]
2\cdot \displaystyle\int_{-2}^{0}(g(x)-f(x))\;\mathrm dx &=& 1,6&\\[5pt]
2\cdot \left(\displaystyle\int_{-2}^{0}a\cdot f(x)\;\mathrm dx - \displaystyle\int_{-2}^{0}f(x)\;\mathrm dx\right) &=& 1,6&\\[5pt]
\end{array}\)](https://mathjax.schullv.de/b9bb0ab11298336e4541abe958210e9fa5d2c389ef8be67550aa2242faf1e0b1?color=5a5a5a) Diese Gleichung kann nun mit dem CAS mit Hilfe des solve-Befehls gelöst werden:
menu
Diese Gleichung kann nun mit dem CAS mit Hilfe des solve-Befehls gelöst werden:
menu  3
3  1
Mit folgendem Befehl kann ein Integral eingefügt werden:
menu
1
Mit folgendem Befehl kann ein Integral eingefügt werden:
menu  4
4  3
Der CAS liefert
3
Der CAS liefert  Der Faktor
Der Faktor  muss folglich den Wert 1,9 betragen, sodass der Flächeninhalt zwischen den Graphen von
muss folglich den Wert 1,9 betragen, sodass der Flächeninhalt zwischen den Graphen von  und
und  im Intervall
im Intervall ![\([2;2]\)](https://mathjax.schullv.de/3b252266fb56353e32d82b9768730c24f6482a733d55acd3df04fedd52ccbb4e?color=5a5a5a)
 beträgt..
beträgt..
4
1. Schritt: Parameter  bestimmen
Der Parameter
bestimmen
Der Parameter  soll so gewählt werden, dass der Tiefpunkt des Graphen der Funktion
soll so gewählt werden, dass der Tiefpunkt des Graphen der Funktion  auf der
auf der  -Achse liegt.
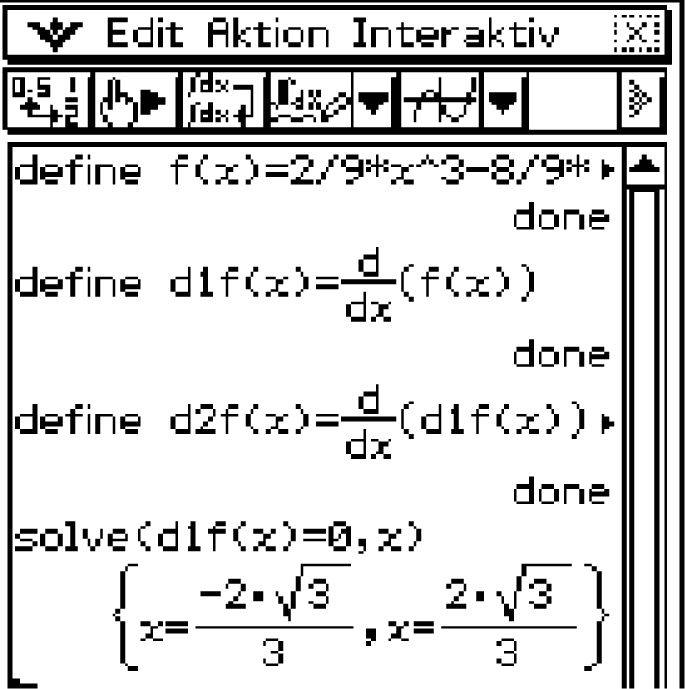
Um die Koordinaten des Tiefpunkts zu bestimmen, müssen die ersten beiden Ableitungen von
-Achse liegt.
Um die Koordinaten des Tiefpunkts zu bestimmen, müssen die ersten beiden Ableitungen von  ermittelt werden und mit dem solve-Befehl des CAS die möglichen Extremstellen berechnet werden.
ermittelt werden und mit dem solve-Befehl des CAS die möglichen Extremstellen berechnet werden.
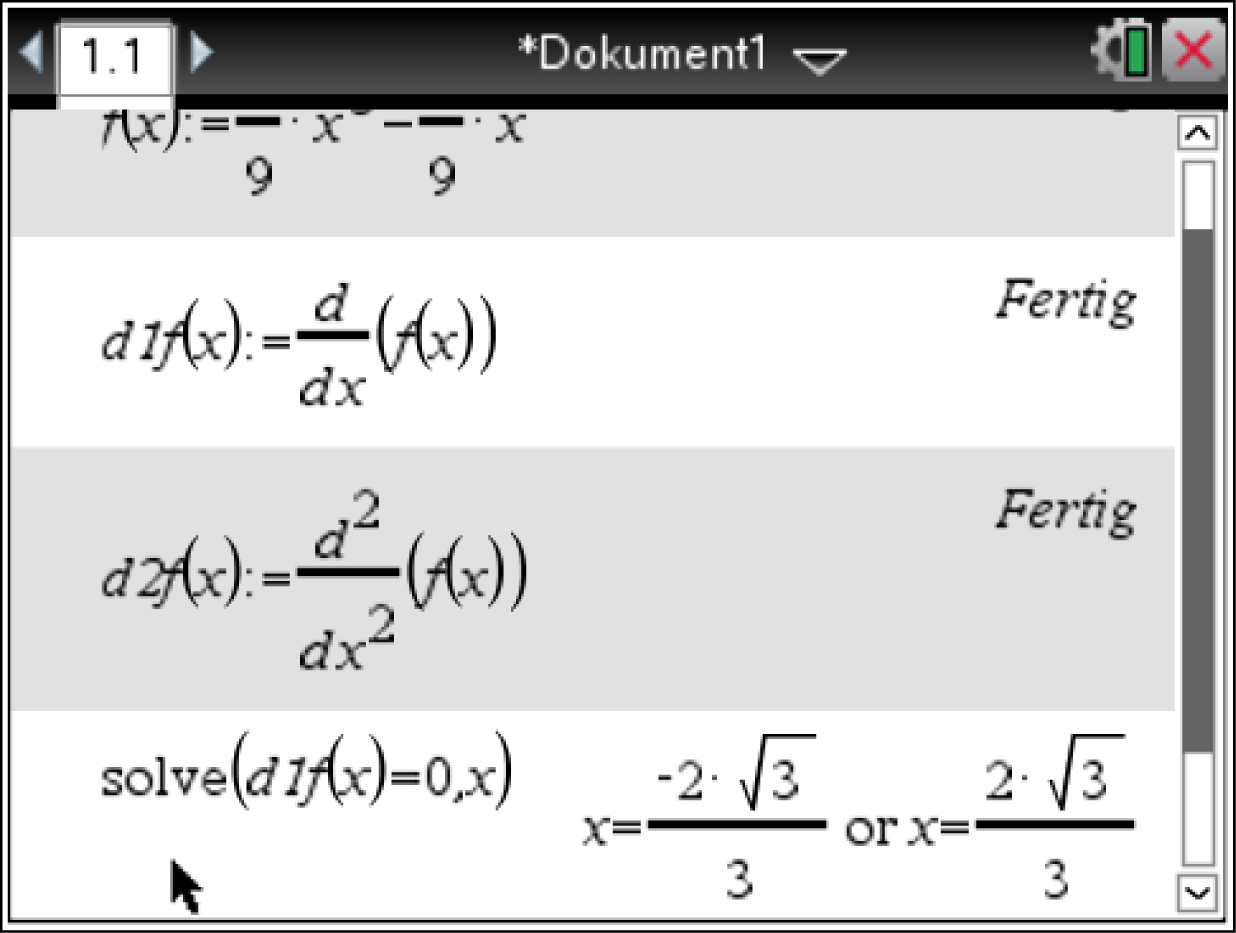 Es ergeben sich
Es ergeben sich  und
und  Anwenden der hinreichenden Bedingung für Extremstellen liefert:
Anwenden der hinreichenden Bedingung für Extremstellen liefert:
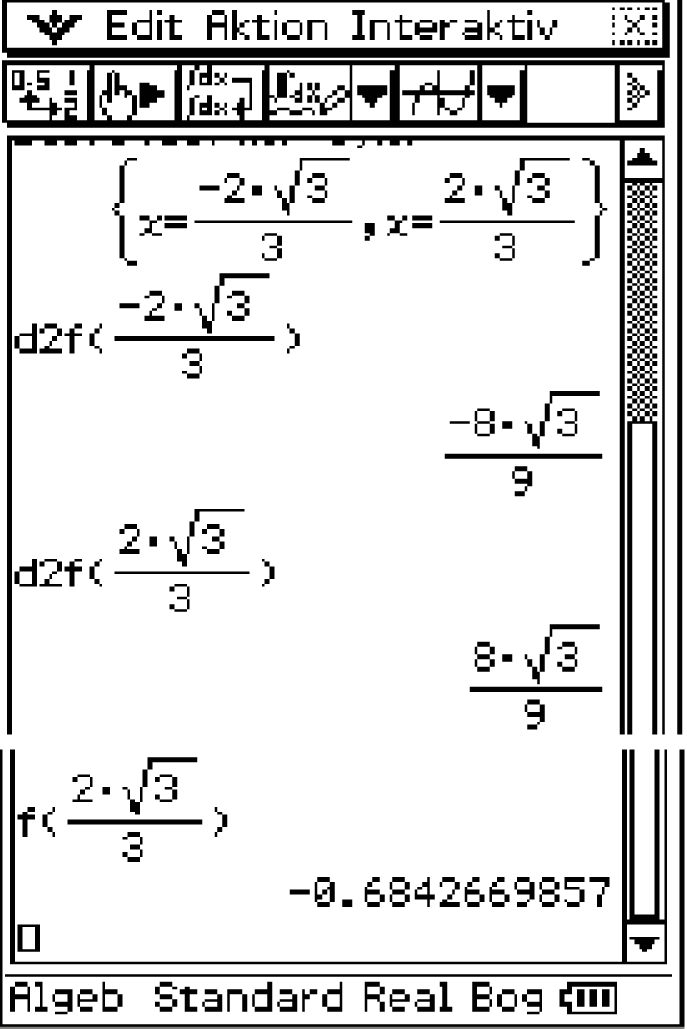
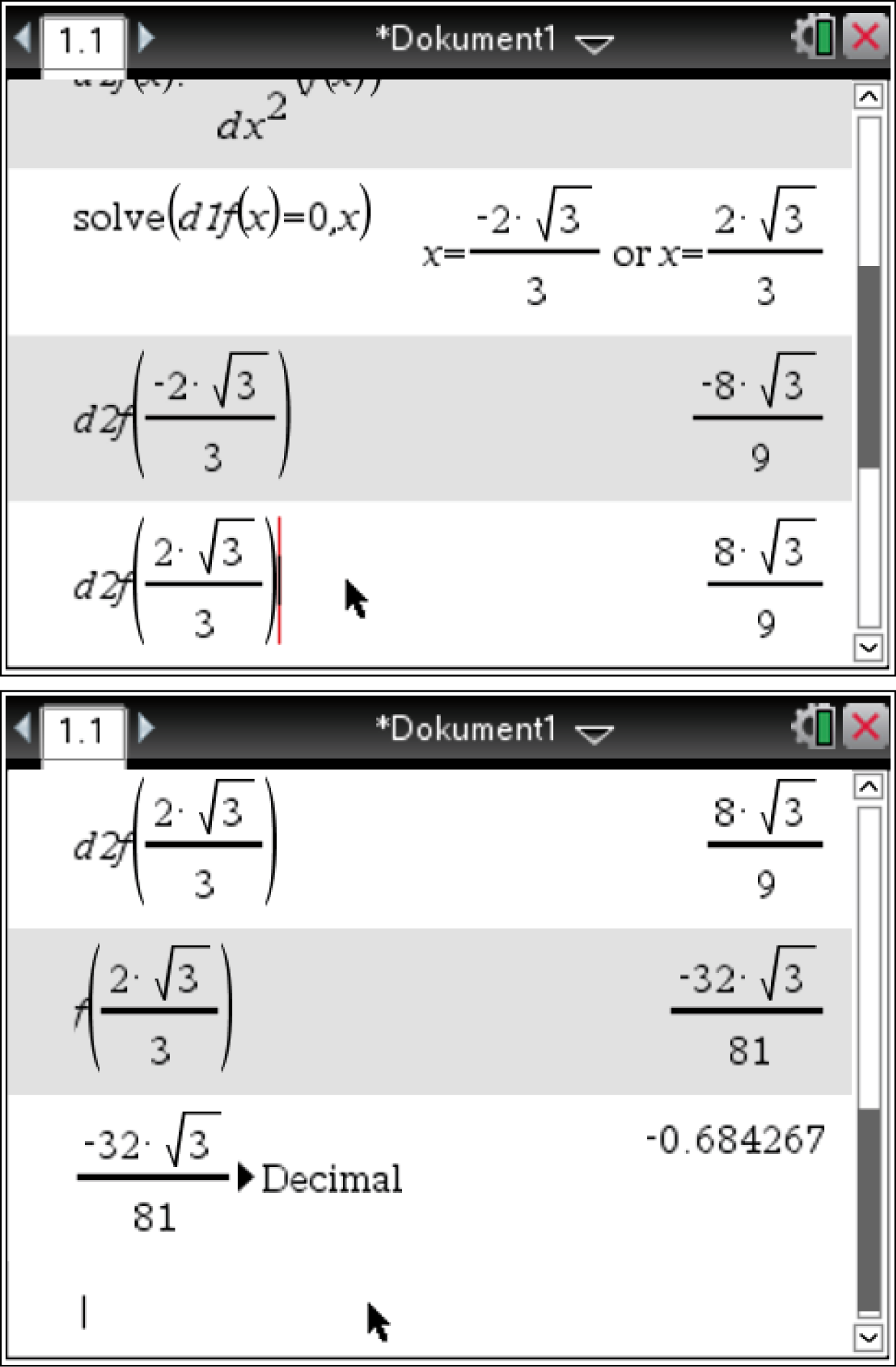 Für den Tiefpunkt muss gelten:
Für den Tiefpunkt muss gelten:  Dieser befindet sich also an der Stelle
Dieser befindet sich also an der Stelle  Berechnen der
Berechnen der  -Koordinate liefert den Tiefpunkt mit
-Koordinate liefert den Tiefpunkt mit  Der Graph von
Der Graph von  muss also um
muss also um  Einheiten in positive
Einheiten in positive  -Richtung verschoben werden.
2. Schritt: Funktionen verschieben
Verschieben der Graphen
-Richtung verschoben werden.
2. Schritt: Funktionen verschieben
Verschieben der Graphen  und
und  um den Faktor
um den Faktor  in positive
in positive  -Richtung ergibt:
-Richtung ergibt:

 3. Schritt: Integrationsgrenzen bestimmen
Die Integrationsgrenzen
3. Schritt: Integrationsgrenzen bestimmen
Die Integrationsgrenzen  und
und  bei der Berechnung eines Rotationskörpers aus der Fläche zwischen zwei Graphen entsprechen den Schnittstellen der beiden Graphen.
Im CAS können die beiden verschobenen Funktionen von
bei der Berechnung eines Rotationskörpers aus der Fläche zwischen zwei Graphen entsprechen den Schnittstellen der beiden Graphen.
Im CAS können die beiden verschobenen Funktionen von  und
und  definiert werden und die Schnittstellen durch Gleichsetzen berechnet werden.
definiert werden und die Schnittstellen durch Gleichsetzen berechnet werden.
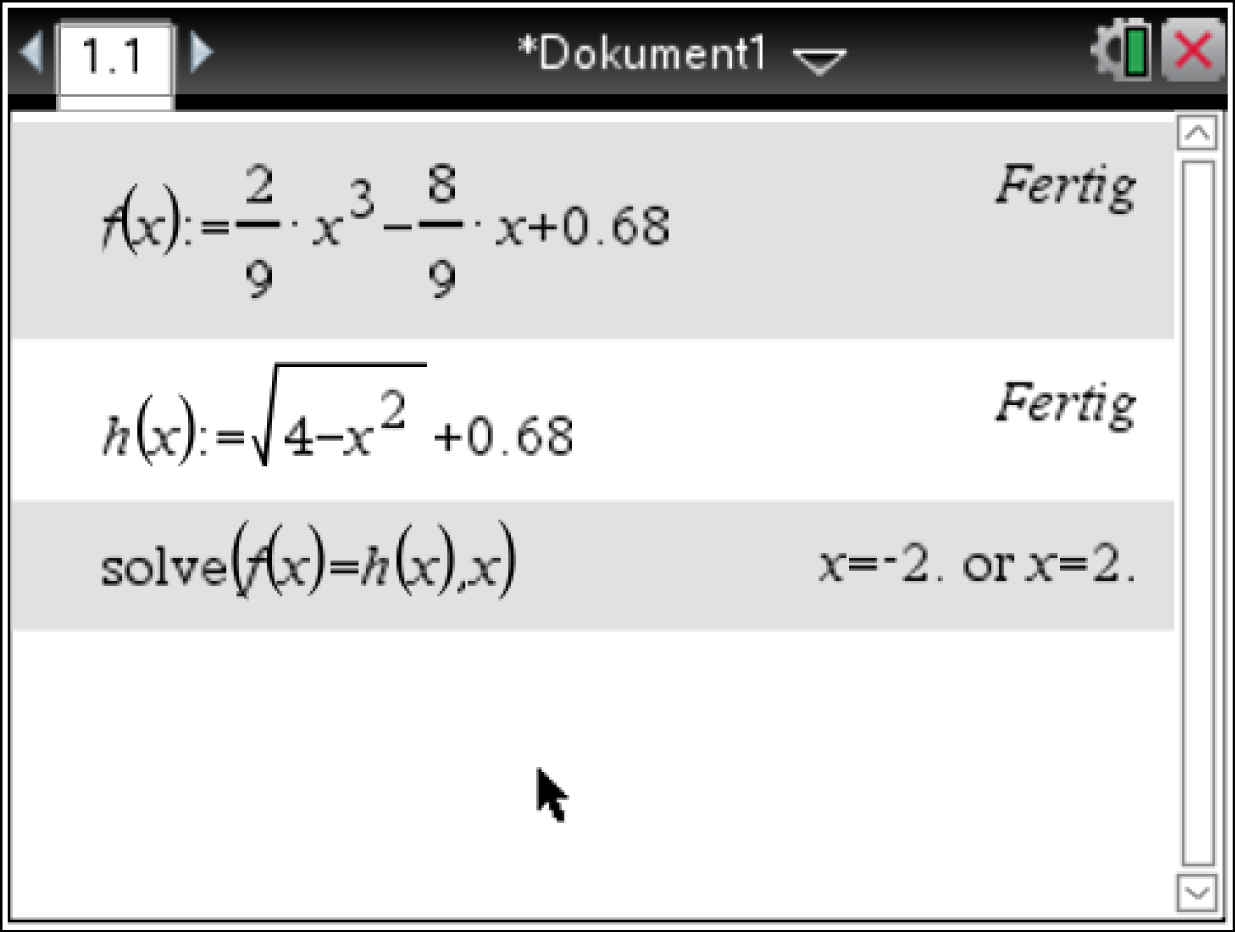 Der CAS liefert die Schnittstellen und somit die Integrationsgrenzen für den Rotationskörper mit:
Der CAS liefert die Schnittstellen und somit die Integrationsgrenzen für den Rotationskörper mit:
 und
und  4. Schritt: Volumen des Rotationskörpers berechnen
Für das Volumen eines Rotationskörpers, der aus einer Fläche entsteht, die von den Graphen zweier Funktionen
4. Schritt: Volumen des Rotationskörpers berechnen
Für das Volumen eines Rotationskörpers, der aus einer Fläche entsteht, die von den Graphen zweier Funktionen  und
und  eingeschlossen wird, gilt:
eingeschlossen wird, gilt:
 Mit dem Befehl menu
Mit dem Befehl menu  4
4  3 kann im CAS ein Integral eingefügt werden. Einsetzen der Integrationsgrenzen
3 kann im CAS ein Integral eingefügt werden. Einsetzen der Integrationsgrenzen  bzw
bzw  ergibt dann:
ergibt dann:
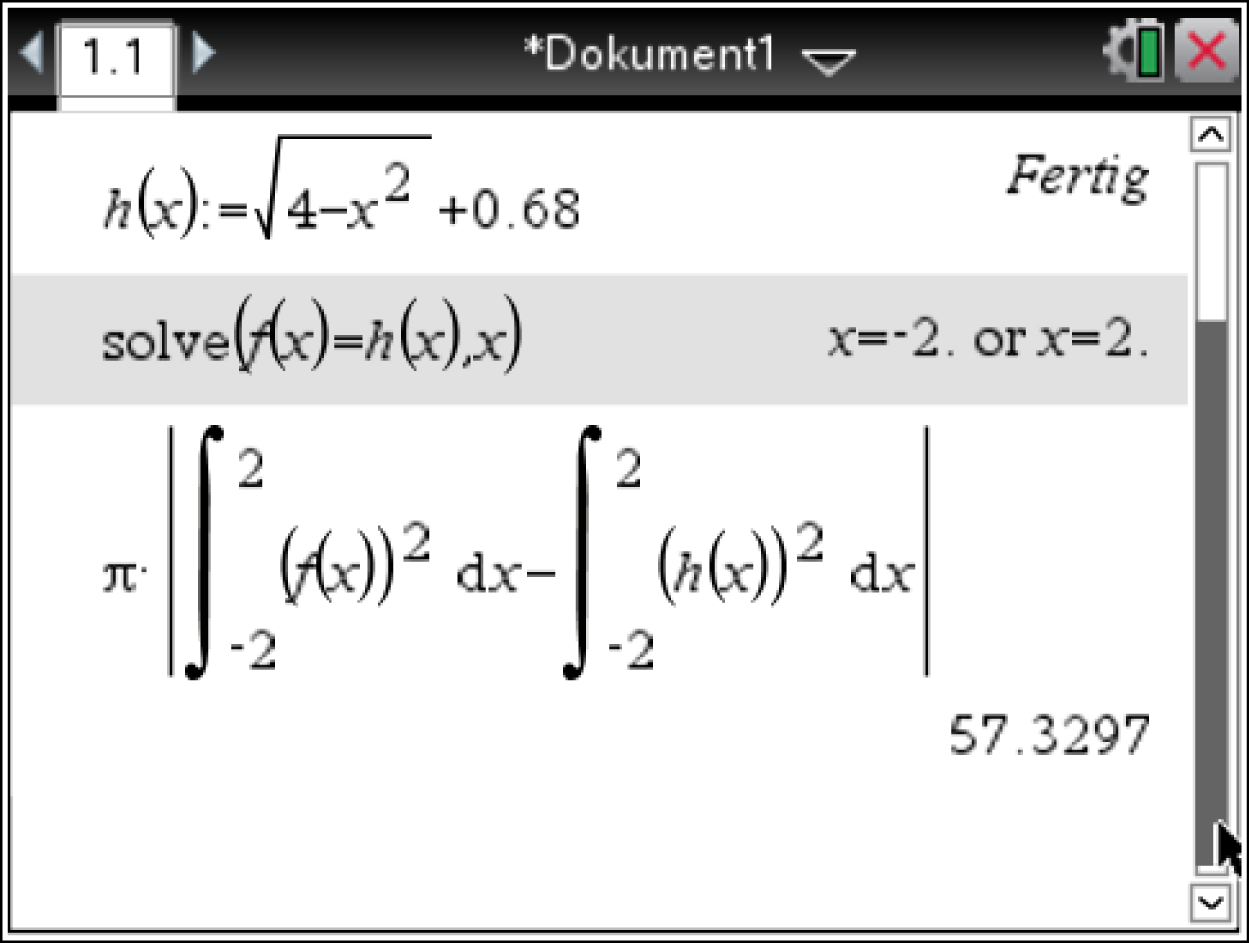 Das Volumen des Rotationskörpers beträgt somit etwa
Das Volumen des Rotationskörpers beträgt somit etwa  5. Schritt: Körper skizzieren
Mit dem CAS können die Graphen der Funktionen
5. Schritt: Körper skizzieren
Mit dem CAS können die Graphen der Funktionen  und
und  graphisch dargestellt werden und eine Wertetabelle angezeigt werden:
graphisch dargestellt werden und eine Wertetabelle angezeigt werden:
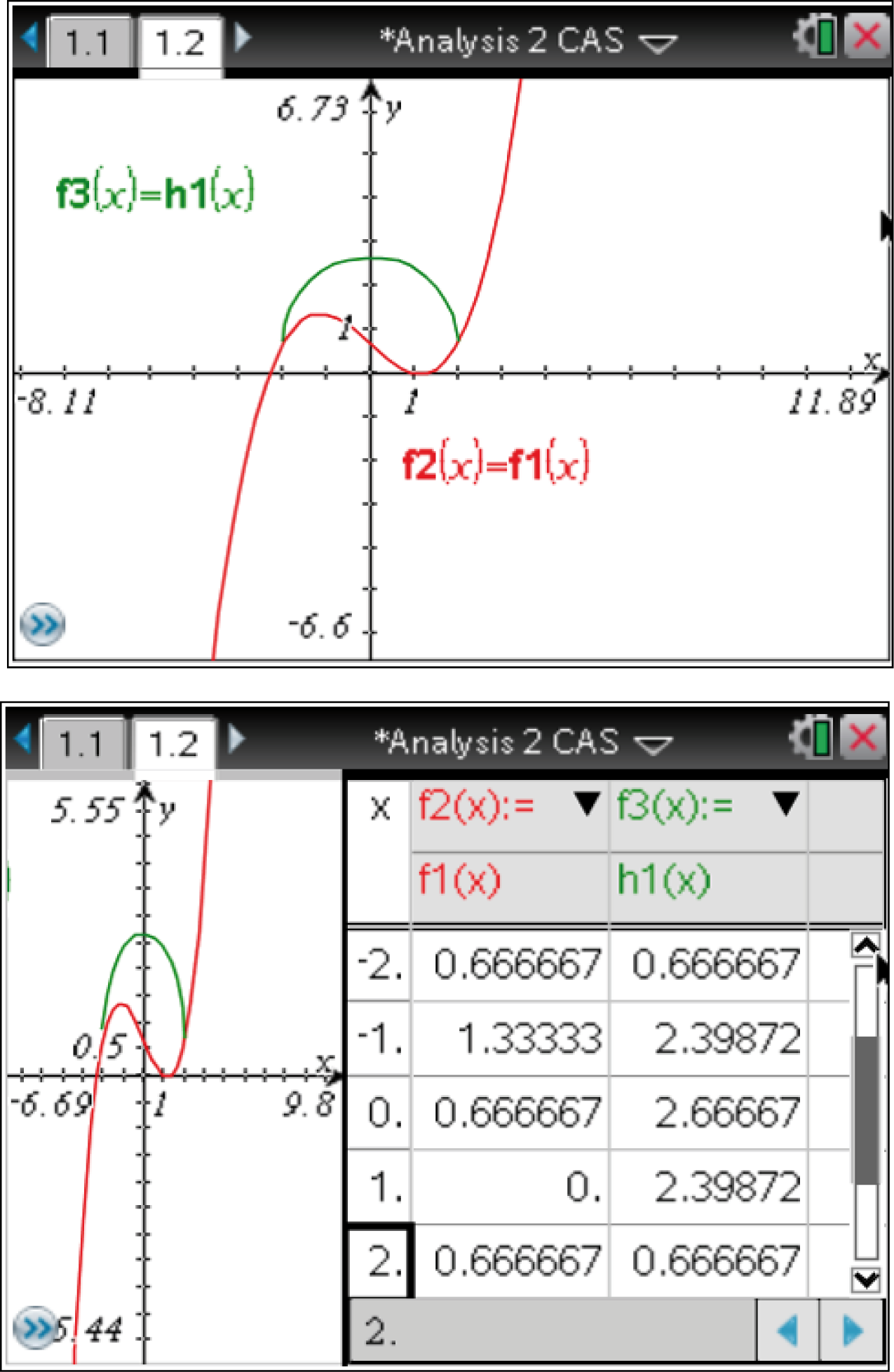 Der entstandene Körper sieht somit wie folgt aus:
Der entstandene Körper sieht somit wie folgt aus:







1
Allgemeine Funktionsgleichung einer Funktion dritten Grades:
 Da die Funktion durch den Ursprung verlaufen soll, muss gelten:
Da die Funktion durch den Ursprung verlaufen soll, muss gelten:
![\(\begin{array}[t]{rll}
f(0)&=& 0 & \\[5pt]
a\cdot 0^3+b\cdot 0^2+c\cdot 0+d&=& 0& \\[5pt]
d&=& 0
\end{array}\)](https://mathjax.schullv.de/5bb5478a8ca462b8e6b94d461ac016403b6526947c5101b5d868f97d86eeff20?color=5a5a5a) Aus dem Graphen von
Aus dem Graphen von  können die Koordinaten von weiteren drei Punkten abgelesen werden. Aus diesen ergibt sich folgendes lineares Gleichungssystem:
Aus Zeile
können die Koordinaten von weiteren drei Punkten abgelesen werden. Aus diesen ergibt sich folgendes lineares Gleichungssystem:
Aus Zeile  folgt
folgt  Einsetzen in Zeile
Einsetzen in Zeile  liefert:
liefert:
![\(\begin{array}[t]{rll}
8a+4\cdot 0+2c&=& 0 &\quad \scriptsize \mid\;-8a \\[5pt]
2c&=& -8a&\quad \scriptsize \mid\; :2 \\[5pt]
c&=& -4a
\end{array}\)](https://mathjax.schullv.de/30117385b21d2fdf267cc6ee2c1aebb844cdc835cb5858d48af765a03a3b7677?color=5a5a5a) Für Zeile
Für Zeile  folgt also:
folgt also:
![\(\begin{array}[t]{rll}
a+b+c&=& -\dfrac{2}{3}& \\[5pt]
a+0-4a&=& -\dfrac{2}{3} &\\[5pt]
-3a&=& -\dfrac{2}{3} &\quad \scriptsize \mid\; :(-3) \\[5pt]
a&=& \dfrac{2}{9}
\end{array}\)](https://mathjax.schullv.de/7aa60d308e442fe1ad4c856bb7f192805fd40c611562a398535ed66513daa7a3?color=5a5a5a) Der Wert von
Der Wert von  ergibt sich nun zu
ergibt sich nun zu  Alternativ kann das lineare Gleichungssystem auch mit Hilfe des CAS durch den Befehl Keyboard
Alternativ kann das lineare Gleichungssystem auch mit Hilfe des CAS durch den Befehl Keyboard  2D gelöst werden.
Die Funktion
2D gelöst werden.
Die Funktion  ist somit gegeben durch:
ist somit gegeben durch:

2
1. Schritt: Flächeninhalt berechnen
Die grau markierte Fläche wird durch die  -Achse in zwei Teilflächen unterteilt:
Die Teilfläche oberhalb der
-Achse in zwei Teilflächen unterteilt:
Die Teilfläche oberhalb der  -Achse entspricht einem Viertel des Kreises. Aus der Abbildung in der Aufgabenstellung kann ein Radius von
-Achse entspricht einem Viertel des Kreises. Aus der Abbildung in der Aufgabenstellung kann ein Radius von  entnommen werden.
Mit der Formel zur Berechnung des Flächeninhalts
entnommen werden.
Mit der Formel zur Berechnung des Flächeninhalts  eines Kreises folgt also:
eines Kreises folgt also:
![\(\begin{array}[t]{rll}
A_1&=& \dfrac{1}{4}\cdot A_K & \\[5pt]
&=& \dfrac{1}{4}\cdot \pi \cdot 2^2 & \\[5pt]
&\approx& 3,14 \; [\text{cm}^2]
\end{array}\)](https://mathjax.schullv.de/d269274d49505263b33920c35cf1d8febba843582c732d70c5bf8b32f58243da?color=5a5a5a) Die Teilfläche unterhalb der
Die Teilfläche unterhalb der  -Achse entspricht der Fläche zwischen dem Graphen von
-Achse entspricht der Fläche zwischen dem Graphen von  und der
und der  -Achse im Intervall
-Achse im Intervall ![\([0;2].\)](https://mathjax.schullv.de/9f001e7a68d1db871d8f573e1477bd4c3a21c6b1fecf3e2c5b0f4e947417ade8?color=5a5a5a) Dieses Integral kann mit dem Befehl menu
Dieses Integral kann mit dem Befehl menu  4
4  3 mit dem CAS gelöst werden und ergibt
3 mit dem CAS gelöst werden und ergibt 
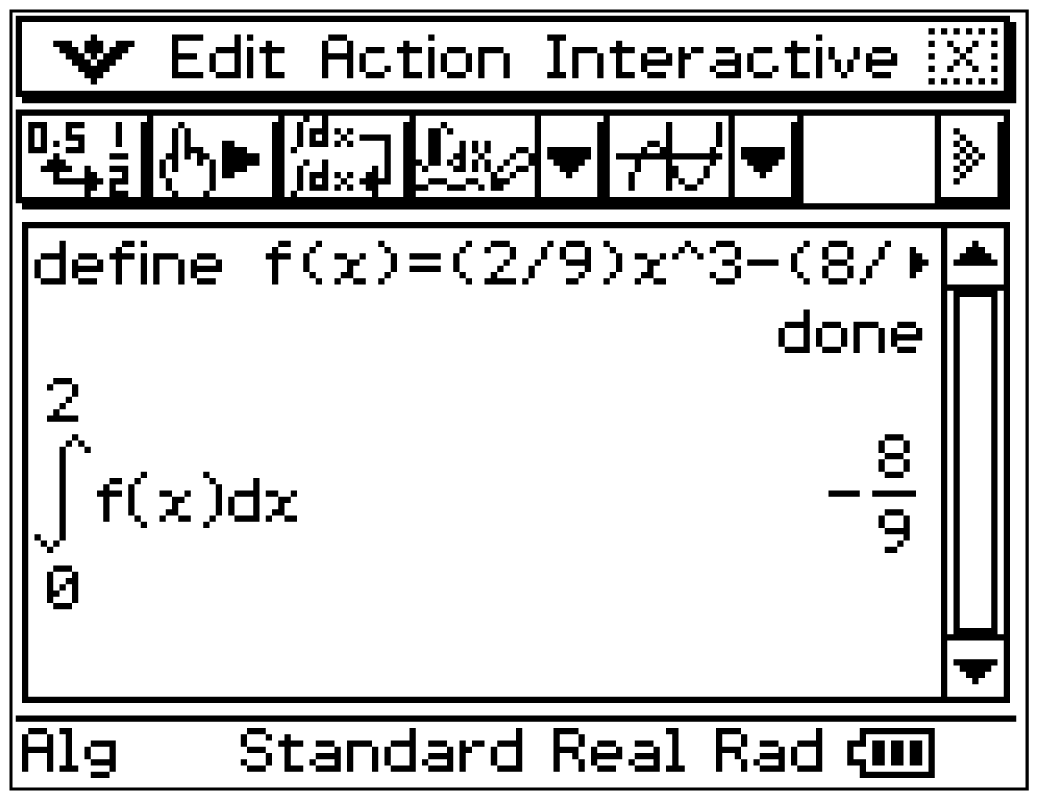 Da die Fläche unterhalb der
Da die Fläche unterhalb der  -Achse liegt und das Integral folglich negativ ist, muss der Betrag des Integrals bestimmt werden. Dieser ergibt sich demnach zu
-Achse liegt und das Integral folglich negativ ist, muss der Betrag des Integrals bestimmt werden. Dieser ergibt sich demnach zu  Der gesamte Flächeninhalt folgt also mit:
Der gesamte Flächeninhalt folgt also mit:
 2. Schritt: Volumen bestimmen
Da die Schichtdicke der Legierung
2. Schritt: Volumen bestimmen
Da die Schichtdicke der Legierung  beträgt, ergibt sich:
beträgt, ergibt sich:
 3. Schritt: Masse berechnen
Da
3. Schritt: Masse berechnen
Da  eine Masse von
eine Masse von  hat, folgt:
hat, folgt:
![\(\begin{array}[t]{rll}
m&=& 0,00403 \;\text{cm}^3 \cdot 12\dfrac{\,\text{g}}{\,\text{cm}^3}& \\[5pt]
&=& 0,04836 \,\text{g}
\end{array}\)](https://mathjax.schullv.de/a45b433c73d91ef60d835a36beca4f33c8d8ff83b5b04082eb4eb0f605745b47?color=5a5a5a) Für die Brosche wird somit eine Legierung von
Für die Brosche wird somit eine Legierung von  benötigt.
benötigt.

3.1
Verschiebung beschreiben
Der Term der Funktion  unterscheidet sich nur durch den zusätzlichen Faktor
unterscheidet sich nur durch den zusätzlichen Faktor  vom Term der Funktion
vom Term der Funktion  Mit
Mit  bewirkt dieser eine Streckung des Graphen von
bewirkt dieser eine Streckung des Graphen von  in
in  -Richtung.
Da der Funktionsgraph nicht verschoben, sondern nur gestreckt wird, bleiben die Nullstellen gleich. Auch die
-Richtung.
Da der Funktionsgraph nicht verschoben, sondern nur gestreckt wird, bleiben die Nullstellen gleich. Auch die  -Koordinate der Extrempunkte verändert sich nicht. Lediglich die
-Koordinate der Extrempunkte verändert sich nicht. Lediglich die  -Koordinate verschiebt sich in positive bzw. negative
-Koordinate verschiebt sich in positive bzw. negative  -Richtung.
Variante skizzieren
Um eine möglich Variante zu skizzieren, wird ein Wert
-Richtung.
Variante skizzieren
Um eine möglich Variante zu skizzieren, wird ein Wert  gewählt und mit dem CAS eine entsprechende Wertetabelle sowie der dazugehörige Graph der Funktion
gewählt und mit dem CAS eine entsprechende Wertetabelle sowie der dazugehörige Graph der Funktion  erstellt.
Für
erstellt.
Für  gilt beispielsweise:
gilt beispielsweise:
![\(\begin{array}[t]{rll}
g_2(x)&=& 2 \cdot f(x)& \\[5pt]
&=& 2 \cdot \left( \dfrac{2}{9} \cdot x^3 - \dfrac{8}{9} \cdot x \right)& \\[5pt]
&=& \dfrac{4}{9} \cdot x^3 - \dfrac{16}{9} \cdot x
\end{array}\)](https://mathjax.schullv.de/36a34e9fbdd620508d55b6332eeb5b328c22a0199f374af97c1debcef5f58029?color=5a5a5a) Das ergänzte Schaubild könnte also beispielsweise wie folgt aussehen:
Das ergänzte Schaubild könnte also beispielsweise wie folgt aussehen:


3.2
Da die beiden Funktionen  und
und  punktsymmetrisch sind, reicht es aus, die Fläche zwischen den beiden Graphen im Intervall
punktsymmetrisch sind, reicht es aus, die Fläche zwischen den beiden Graphen im Intervall ![\([-2;0]\)](https://mathjax.schullv.de/ffa38fea12f21af699510ecb456a1b88004ec0bac75ab7ac604cef40541ad9d8?color=5a5a5a) zu betrachten. Das doppelte dieser Fläche soll dann
zu betrachten. Das doppelte dieser Fläche soll dann  betragen.
Für den Flächeninhalt zwischen den Graphen von
betragen.
Für den Flächeninhalt zwischen den Graphen von  und
und  im Intervall
im Intervall ![\([-2;0]\)](https://mathjax.schullv.de/ffa38fea12f21af699510ecb456a1b88004ec0bac75ab7ac604cef40541ad9d8?color=5a5a5a) gilt:
gilt:
![\(\begin{array}[t]{rll}
A&=& 1,6 &\\[5pt]
2\cdot \displaystyle\int_{-2}^{0}(g(x)-f(x))\;\mathrm dx &=& 1,6&\\[5pt]
2\cdot \left(\displaystyle\int_{-2}^{0}a\cdot f(x)\;\mathrm dx - \displaystyle\int_{-2}^{0}f(x)\;\mathrm dx\right) &=& 1,6&\\[5pt]
\end{array}\)](https://mathjax.schullv.de/b9bb0ab11298336e4541abe958210e9fa5d2c389ef8be67550aa2242faf1e0b1?color=5a5a5a) Diese Gleichung kann nun mit dem CAS mit Hilfe des solve-Befehls gelöst werden:
Interactive
Diese Gleichung kann nun mit dem CAS mit Hilfe des solve-Befehls gelöst werden:
Interactive  Calc
Calc  Solve
Mit folgendem Befehl kann ein Integral eingefügt werden:
Interactive
Solve
Mit folgendem Befehl kann ein Integral eingefügt werden:
Interactive  adv
adv 

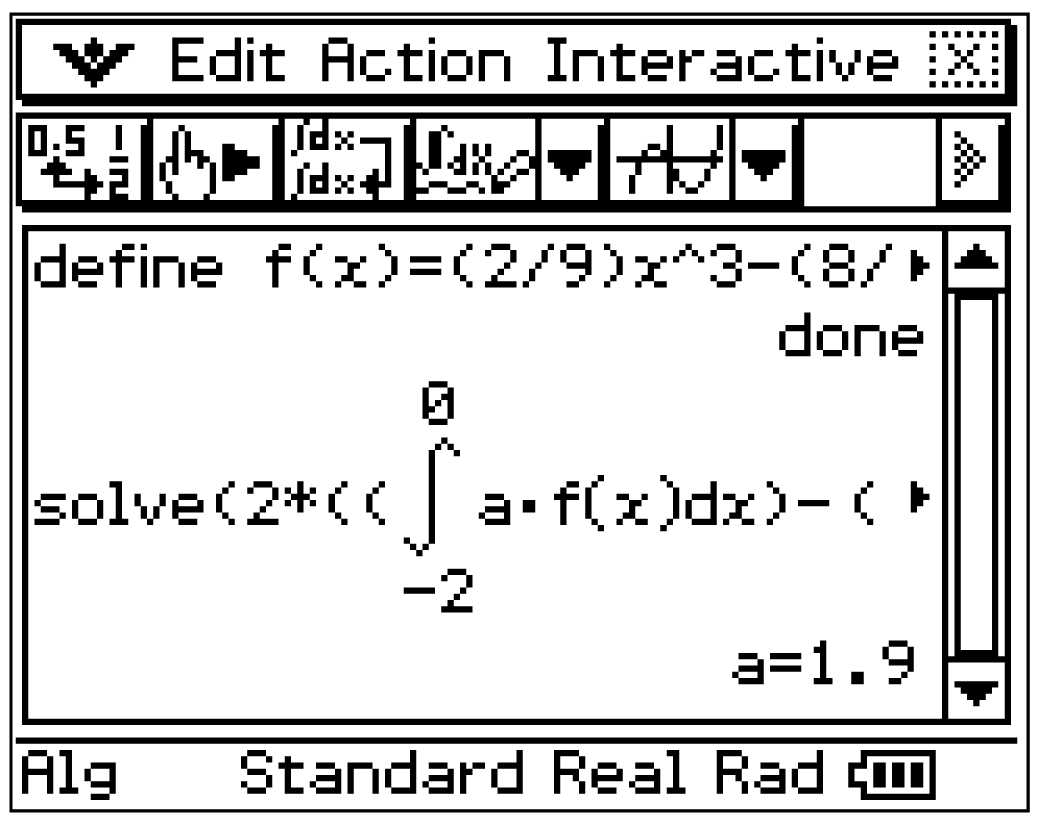 Der CAS liefert
Der CAS liefert  Der Faktor
Der Faktor  muss folglich den Wert 1,9 betragen, sodass der Flächeninhalt zwischen den Graphen von
muss folglich den Wert 1,9 betragen, sodass der Flächeninhalt zwischen den Graphen von  und
und  im Intervall
im Intervall ![\([2;2]\)](https://mathjax.schullv.de/3b252266fb56353e32d82b9768730c24f6482a733d55acd3df04fedd52ccbb4e?color=5a5a5a)
 beträgt..
beträgt..

4
1. Schritt: Parameter  bestimmen
Der Parameter
bestimmen
Der Parameter  soll so gewählt werden, dass der Tiefpunkt des Graphen der Funktion
soll so gewählt werden, dass der Tiefpunkt des Graphen der Funktion  auf der
auf der  -Achse liegt.
Um die Koordinaten des Tiefpunkts zu bestimmen, müssen die ersten beiden Ableitungen von
-Achse liegt.
Um die Koordinaten des Tiefpunkts zu bestimmen, müssen die ersten beiden Ableitungen von  ermittelt werden und mit dem solve-Befehl des CAS die möglichen Extremstellen berechnet werden.
ermittelt werden und mit dem solve-Befehl des CAS die möglichen Extremstellen berechnet werden.
 Es ergeben sich
Es ergeben sich  und
und  Anwenden der hinreichenden Bedingung für Extremstellen liefert:
Anwenden der hinreichenden Bedingung für Extremstellen liefert:
 Für den Tiefpunkt muss gelten:
Für den Tiefpunkt muss gelten:  Dieser befindet sich also an der Stelle
Dieser befindet sich also an der Stelle  Berechnen der
Berechnen der  -Koordinate liefert den Tiefpunkt mit
-Koordinate liefert den Tiefpunkt mit  Der Graph von
Der Graph von  muss also um
muss also um  Einheiten in positive
Einheiten in positive  -Richtung verschoben werden.
2. Schritt: Funktionen verschieben
Verschieben der Graphen
-Richtung verschoben werden.
2. Schritt: Funktionen verschieben
Verschieben der Graphen  und
und  um den Faktor
um den Faktor  in positive
in positive  -Richtung ergibt:
-Richtung ergibt:

 3. Schritt: Integrationsgrenzen bestimmen
Die Integrationsgrenzen
3. Schritt: Integrationsgrenzen bestimmen
Die Integrationsgrenzen  und
und  bei der Berechnung eines Rotationskörpers aus der Fläche zwischen zwei Graphen entsprechen den Schnittstellen der beiden Graphen.
Im CAS können die beiden verschobenen Funktionen von
bei der Berechnung eines Rotationskörpers aus der Fläche zwischen zwei Graphen entsprechen den Schnittstellen der beiden Graphen.
Im CAS können die beiden verschobenen Funktionen von  und
und  definiert werden und die Schnittstellen durch Gleichsetzen berechnet werden.
definiert werden und die Schnittstellen durch Gleichsetzen berechnet werden.
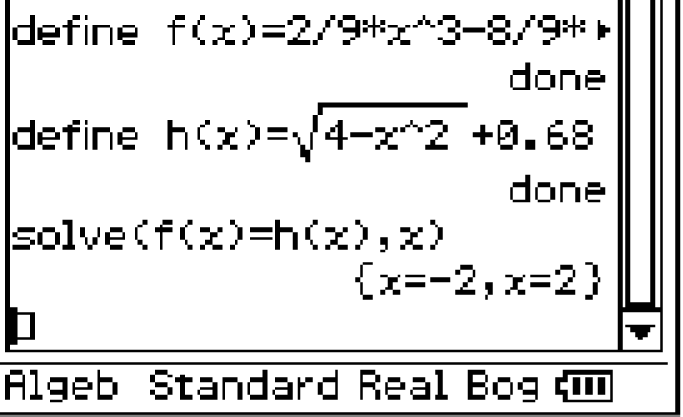 Der CAS liefert die Schnittstellen und somit die Integrationsgrenzen für den Rotationskörper mit:
Der CAS liefert die Schnittstellen und somit die Integrationsgrenzen für den Rotationskörper mit:
 und
und  4. Schritt: Volumen des Rotationskörpers berechnen
Für das Volumen eines Rotationskörpers, der aus einer Fläche entsteht, die von den Graphen zweier Funktionen
4. Schritt: Volumen des Rotationskörpers berechnen
Für das Volumen eines Rotationskörpers, der aus einer Fläche entsteht, die von den Graphen zweier Funktionen  und
und  eingeschlossen wird, gilt:
eingeschlossen wird, gilt:
 Mit dem Befehl menu
Mit dem Befehl menu  4
4  3 kann im CAS ein Integral eingefügt werden. Einsetzen der Integrationsgrenzen
3 kann im CAS ein Integral eingefügt werden. Einsetzen der Integrationsgrenzen  bzw
bzw  ergibt dann:
ergibt dann:
 Das Volumen des Rotationskörpers beträgt somit etwa
Das Volumen des Rotationskörpers beträgt somit etwa  5. Schritt: Körper skizzieren
Mit dem CAS können die Graphen der Funktionen
5. Schritt: Körper skizzieren
Mit dem CAS können die Graphen der Funktionen  und
und  graphisch dargestellt werden und eine Wertetabelle angezeigt werden:
graphisch dargestellt werden und eine Wertetabelle angezeigt werden:
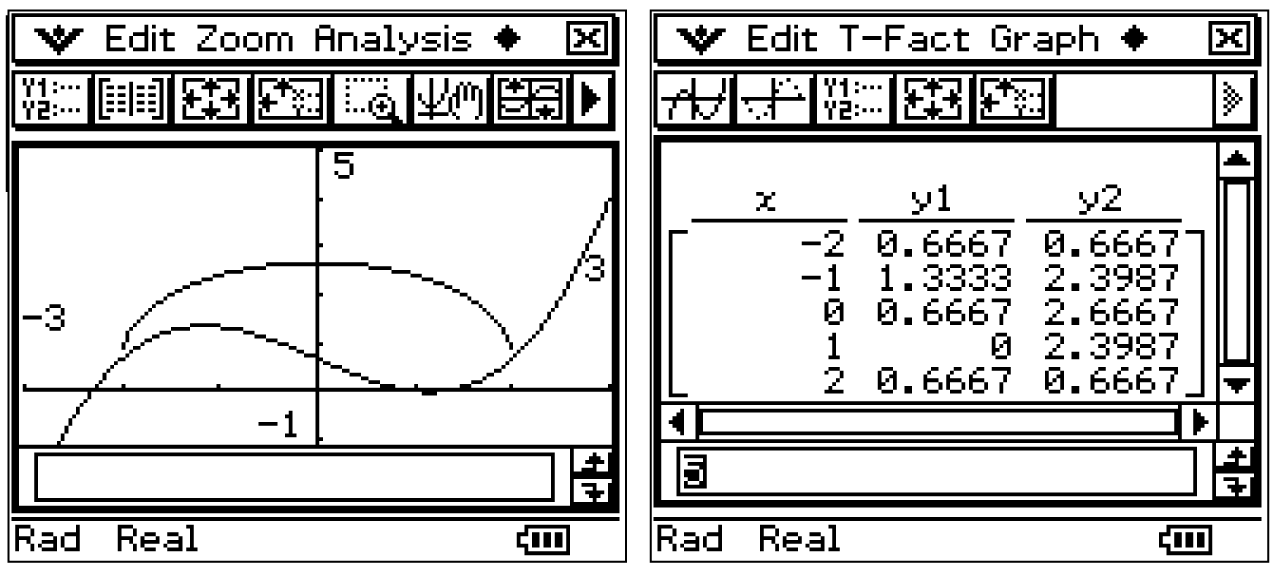 Der entstandene Körper sieht somit wie folgt aus:
Der entstandene Körper sieht somit wie folgt aus: