C1 - Lineare Algebra/ Analytische Geometrie

Der Turm des One-World-Trade-Centers in New York ist (ohne Spitze) ca. $420 \,\text{m}$ hoch (Abbildung 1).

Die Grund- und Dachfläche des Turms sind quadratisch und liegen parallel zueinander, wobei die Dachfläche kleiner als die Grundfläche ist. Die Eckpunkte der Dachfläche liegen jeweils vertikal oberhalb der Mittelpunkte der Seiten der Grundfläche.

Die Außenwände des Turms bestehen aus acht Dreiecksflächen. Vier zueinander kongruente Dreiecke weisen mit der Spitze nach unten, vier zueinander kongruente Dreiecke weisen mit der Spitze nach oben.

Der Gebäudesockel wird in der folgenden Aufgabenstellung vernachlässigt.

Abbildung 1

Im Modell hat die quadratische Grundfläche des Turms die Eckpunkte $A(-4\mid2\mid0),\; B, \; C(4\mid-2\mid 0)$ und $D(2\mid4\mid 0).$

Die quadratische Dachfläche hat (in entsprechender Reihenfolge) die Eckpunkte $E,\; F,\; G(3\mid1\mid42)$ und $H.$

Der Punkt $G$ liegt vertikal über dem Mittelpunkt der Seite $\overline{CD}.$ Der Erdboden wird durch die $xy$ -Ebene beschrieben. Eine Längeneinheit entspricht 10 Meter.

1.1

Zeichne den Grundriss der Grundfläche in das Koordinatensystem in Abbildung 2 ein.

Zeichne den Grundriss der Dachfläche ebenfalls in das Koordinatensystem ein.

Gib die Koordinaten der Punkte $B,\; E,\; F$ und $H$ an.

Grundriss Grundfläche Koordinatensystem One World Trade Center

Abbildung 2

(6 BE)

1.2

Das Dreieck $CDG$ liegt in der Ebene $L.$

Gib eine Gleichung der Ebene $L$ in Parameterform an und bestimme eine Gleichung der Ebene $L$ in Koordinatenform.

Beschreibe die besondere Lage der Ebene $L$ im Koordinatensystem.

(7 BE)

1.3

Das Dreieck $CGF$ liegt in der Ebene $M.$

1.3.1

Zeige, dass $84 x-42 y+5 z=420$ eine Gleichung der Ebene $M$ ist.

(2 BE)

1.3.2

Im Rahmen der Planung des Gebäudes wird die im Kasten angegebene Rechnung durchgeführt.

Erläutere $\text{I}$ und $\text{II}$ im Sachzusammenhang.

Deute das Ergebnis in $\text{III}$ in Bezug auf das Gebäude.

Rechnung anzeigen

(4 BE)

1.4

Berechne den Gesamtflächeninhalt der acht Dreiecke, aus denen die Außenwände des Turms bestehen, in Quadratmeter.

(8 BE)

1.5

Im Mittelpunkt der Dachfläche des Turms ist eine Antenne montiert. Im Modell befindet sich die Antennenspitze im Punkt $S(0\mid 0\mid 54).$

Zu einem bestimmten Zeitpunkt fallen Sonnenstrahlen in Richtung des Vektors $\overrightarrow{u}=\pmatrix{1\\\dfrac{1}{3}\\-4}$ auf das Gebäude.

Bestimme die Koordinaten des Schattenpunkts $\(S$ der Antennenspitze auf dem Erdboden unter der Annahme, dass es rings um das Gebäude keine weitere Bebauung gibt.

(5 BE)

Der Turm besitzt im 100. Stock eine Aussichtsplattform, die für Besucher geöffnet ist. Ein reguläres Ticket kostet 32 Dollar, Senioren zahlen 30 Dollar und Kinder 26 Dollar.

An einem Tag werden 10000 Tickets verkauft. Die Tageseinnahmen betragen 308000 Dollar. Diese Angaben wurden in das angegebene Gleichungssystem überführt:

$\begin{array}{lrll} \text{I}\quad& r+s+ k&=& 10000 &\\ \text{II}\quad& 32r+30s+26k &=& 308000 &\quad \\ \end{array}$

2.1

Gib die Bedeutung der Variablen $r,\; s$ und $k$ an und erläutere die Bedeutung der Gleichung $\text{II}$ im Sachzusammenhang.

(2 BE)

2.2

Berechne die Lösungsmenge des linearen Gleichungssystems und gib eine im Sachzusammenhang mögliche Lösung an.

(6 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Grundrisse zeichnen

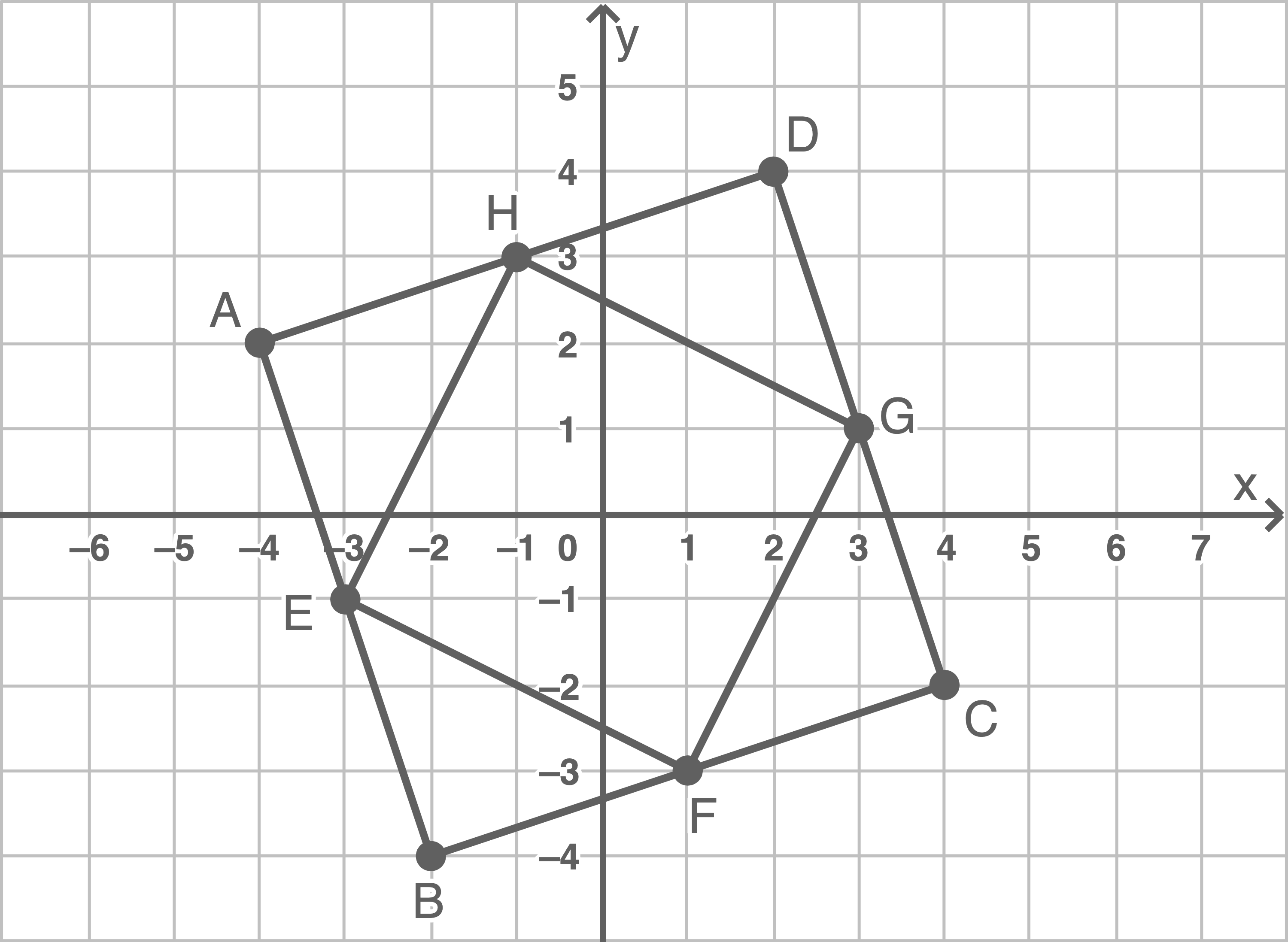One World Trade Center Grundrisse Hessen Abi 2023

Koordinaten angeben

Da die Grundfläche quadratisch sein soll, folgt:

$B(-2\mid -4 \mid 0)$

Die Eckpunkte der Dachfläche liegen vertikal oberhalb der Mittelpunkte der Seiten der Grundfläche auf gleicher Höhe wie $G.$ Somit ergibt sich:

$E(-3 \mid -1 \mid 42)$

$F(1 \mid -3 \mid 42)$

$H(-1 \mid 3 \mid 42)$

1.2

Parametergleichung angeben

Parametergleichung anzeigen

Koordinatenform bestimmen

Ein Normalenvektor $\overrightarrow{n}$ von $L$ folgt mit dem Kreuzprodukt der beiden Spannvektoren:

$\begin{array}[t]{rll} \overrightarrow{n}&=& \pmatrix{-2\\6\\0} \times \pmatrix{-1\\3\\42}& \\[5pt] &=& \pmatrix{6\cdot 42-0\cdot 3\\0\cdot (-1)-(-2)\cdot 42\\(-2)\cdot 3-6\cdot (-1)} & \\[5pt] &=& \pmatrix{42\cdot 6\\42\cdot 2\\0} & \\[5pt] &=& 42\cdot \pmatrix{ 6\\ 2\\0} \end{array}$

Mit dem Ansatz $\overrightarrow{n} \circ \overrightarrow{x}=\overrightarrow{n} \circ \overrightarrow{a}$ zur Bestimmung der Koordinatengleichung, wobei $\overrightarrow{a}$ den Ortsvektor eines beliebigen Punkts der Ebene beschreibt, ergibt sich nun:

$\begin{array}[t]{rll} \pmatrix{ 6\\ 2\\0}\circ \pmatrix{x\\y\\z}&=& \pmatrix{ 6\\ 2\\0}\circ \pmatrix{4\\-2\\0} & \\[5pt] 6x+2y+0z&=& 6\cdot 4+2\cdot (-2)+0\cdot 0 & \\[5pt] 6x+2y&=& 20 \end{array}$

Eine Gleichung der Ebene $L$ in Koordinatenform ist somit beispielsweise $L: 6x+2y=20.$

Lage beschreiben

Die Ebene $L$ liegt parallel zur $z$ -Achse.

1.3.1

Für eine Gleichung der Ebene $M$ muss gelten, dass die Koordinaten aller drei Punkte diese Gleichung erfüllen.

Einsetzen der Koordinaten von $C,$ $G$ und $F$ liefert:

$\begin{array}[t]{rll} 84\cdot 4-42\cdot (-2)+5\cdot 0&=& 420& \\[5pt] 420&=& 420 \end{array}$

$\begin{array}[t]{rll} 84\cdot 3-42\cdot 1+5\cdot 42&=& 420& \\[5pt] 420&=& 420 \end{array}$

$\begin{array}[t]{rll} 84\cdot 1-42\cdot (-3)+5\cdot 42&=& 420& \\[5pt] 420&=& 420 \end{array}$

Somit folgt, dass alle drei Punkte in der Ebene liegen, die von der Gleichung $84x-42y+5z = 420$ beschrieben wird. Die gegebene Koordinatengleichung ist also eine Gleichung der Ebene $M.$

1.3.2

Schritt $\text{I}$ erläutern

Der Vektor $\overrightarrow{n_M}$ stellt einen Normalenvektor der Ebene $M$ und somit der Ebene von einem der kongruenten Dreiecke, die mit der Spitze nach unten weisen, dar.

Der Vektor $\overrightarrow{n_{Gr}}$ stellt einen Normalenvektor des Bodens und damit auch der Grundfläche des Turms dar.

Schritt $\text{II}$ erläutern

In diesem Rechenschritt wird der Winkel zwischen der Grundfläche und der nach unten weisenden dreieckigen Seitenfläche $CGF$ berechnet.

Ergebnis deuten

Die nach unten weisenden Dreiecksflächen des Turms sind in einem Winkel von etwa $86,95^{\circ}$ gegenüber der Grundfläche geneigt.

1.4

1. Schritt: Flächeninhalt der Dreiecke, die nach oben weisen, berechnen

Betrachtet wird das Dreieck $CDG.$

Die Höhe des Dreiecks entspricht der Höhe des Turms und somit $420\,\text{m}.$

Die Grundseite des Dreiecks ergibt sich beispielsweise durch $\left| \overrightarrow{CD} \right|.$

Der Flächeninhalt von $CDG$ folgt mit:

$A_1 \approx 132,8 \left[\,\text{FE}\right]$

Rechenweg anzeigen

2. Schritt: Flächeninhalt der Dreiecke, die nach unten weisen, berechnen

Betrachtet wird das Dreieck $CGF.$

Mit dem Kreuzprodukt kann der Flächeninhalt berechnet werden:

$\begin{array}[t]{rll} A_2 &=& \dfrac{1}{2}\cdot \left| \overrightarrow{CG} \times \overrightarrow{CF}\right| \\[5pt] &=& \dfrac{1}{2}\cdot \left| \pmatrix{-1\\3\\42}\times \pmatrix{-3\\-1\\42}\right| \\[5pt] &=& \dfrac{1}{2}\cdot \left| \pmatrix{ 3\cdot 42 -42 \cdot (-1) \\ 42 \cdot (-3) -(-1)\cdot 42 \\ -1\cdot (-1) -3\cdot (-3)}\right| \\[5pt] &=& \dfrac{1}{2}\cdot \left| \pmatrix{ 4\cdot 42 \\ -2\cdot 42 \\ 10}\right| \\[5pt] &=& \left| \pmatrix{ 84 \\ - 42 \\ 5}\right| \\[5pt] &=& \sqrt{84^2 +(-42)^2 +5^2} \\[5pt] &\approx& 94,0 \end{array}$

3. Schritt: Gesamtflächeninhalt berechnen

Da die nach oben bzw. nach unten weisenden Dreicke jeweils kongruent zueinander sind folgt:

$\begin{array}[t]{rll} A_{Ges}&=& 4\cdot A_1+4\cdot A_2& \\[5pt] &\approx& 4\cdot 132,8 + 4\cdot 94,0& \\[5pt] &=& 907,2 \left[\,\text{FE} \right] \end{array}$

Der Gesamtflächeninhalt der acht Dreiecke entspricht somit etwa $90\,720 \,\text{m}^2.$

1.5

Geradengleichung des Sonnenstrahls, der auf die Antennenspitze trifft, aufstellen:

$\begin{array}[t]{rll} g: \overrightarrow{x}&=& \overrightarrow{OS} +t\cdot \overrightarrow{u} & \\[5pt] \overrightarrow{x} &=& \pmatrix{0\\0\\54} +t\cdot \pmatrix{1\\\dfrac{1}{3}\\-4} \end{array}$

Der Schattenpunkt $\(S$ der Antennenspitze entspricht dem Schnittpunkt der Geraden $g$ mit der $xy$ -Ebene, welche den Erdboden darstellt.

Eine Ebenengleichung des Erdbodens ist gegeben durch $E: z=0.$

Für die Punkte auf $g$ gilt: $x= t,$ $y= \frac{1}{3}t,$ $z = 54-4t.$ Einsetzen in $E$ liefert:

$\begin{array}[t]{rll} 54-4t&=& 0 &\quad \scriptsize \mid\; +4t\\[5pt] 54&=& 4t &\quad \scriptsize \mid\; :4\\[5pt] 13,5&=& t \end{array}$

Für den Schattenpunkt $\(S$ gilt also:

$\begin{array}[t]{rll} \overrightarrow{OS}&=& \pmatrix{0\\0\\54} +13,5 \cdot \pmatrix{1\\\dfrac{1}{3}\\-4}& \\[5pt] &=& \pmatrix{13,5\\4,5\\0} \end{array}$

Die Koordinaten des Schattenpunkts $\(S$ der Antennenspitze auf dem Erdboden sind gegeben durch $\(S$

2.1

Die Variable $r$ beschreibt die Anzahl der Besucher, die am beobachteten Tag ein reguläres Ticket gekauft haben.

Die Variable $s$ beschreibt die Anzahl der Senioren und die Variable $k$ beschreibt die Anzahl der Kinder, die am beobachteten Tag ein Ticket gekauft haben.

Mit der Gleichung $\text{II}$ werden folglich die Tageseinnahmen berechnet, indem die Besucheranzahlen der drei Kategorien mit dem jeweiligen Ticketpreis multipliziert werden.

2.2

Da das Gleichungssystem aus 3 Variablen aber nur aus 2 Gleichungen besteht, bleibt eine Variable unbestimmt und das Gleichungssystem besitzt folglich unendlich viele Lösungen.

Aus der ersten Zeile folgt:

Rechenweg anzeigen