D – Stochastik
1
Bei einer Studie über das Kaufverhalten von Kunden einer Baumarktkette werden ausschließlich Kunden, die sich registrieren ließen, betrachtet. Aus dem Kreis dieser Kunden wird eine Person zufällig ausgewählt.
Betrachtet werden folgende Ereignisse:
aller Kunden Treuekunden und 
aller Kunden Morgenkunden sind.
„Die Person ist sogenannter Treuekunde, d.h. sie ist bereits länger als fünf Jahre ein registrierter Kunde der Baumarktkette.“
„Die Person ist sogenannter Morgenkunde, d.h. sie kauft überwiegend vor 10 Uhr ein.“
Bei dieser Studie wurde festgestellt, dass
1.1
Es gilt 
Interpretiere diese Gleichung im Sachzusammenhang.
(2 BE)
1.2
Stelle den Sachverhalt in einer vollständig ausgefüllten Vierfeldertafel dar.
(3 BE)
1.3
Ermittle die Wahrscheinlichkeit dafür, dass die ausgewählte Person entweder ein Treuekunde oder ein Morgenkunde ist.
(2 BE)
1.4
Untersuche, ob die Ereignisse 
und 
stochastisch unabhängig sind.
(3 BE)
2
Im Rahmen einer Werbeaktion wird in einem Baumarkt der Kette ein Gewinnspiel mit einem Glücksrad angeboten.
Das Glücksrad besteht aus gleich großen Sektoren, von denen einige mit 
und die anderen mit 
beschriftet sind. Bei diesem Gewinnspiel dreht eine Person zweimal das Glücksrad. Das Produkt der beiden dabei erzielten Zahlen entspricht dem Rabatt in Prozent, der dieser Person beim nächsten Einkauf gewährt wird.
Die Wahrscheinlichkeit dafür, in beiden Drehungen die Zahl zu erzielen, beträgt 
und die Wahrscheinlichkeit dafür, den kleinstmöglichen Rabatt zu erzielen, beträgt 
2.1
Stelle das dem Gewinnspiel zugrundeliegende Zufallsexperiment in einem beschrifteten Baumdiagramm dar.
(3 BE)
2.2
Betrachtet werden sieben Personen, die nacheinander jeweils einmal am Gewinnspiel teilnehmen.
Berechne die Wahrscheinlichkeit dafür, dass dabei genau viermal der kleinstmögliche Rabatt erzielt wird und dies bei vier Personen unmittelbar hintereinander.
(3 BE)
2.3
Um die Werbeaktion attraktiver zu gestalten, setzt die Geschäftsführung des Baumarkts ein anderes Glücksrad ein, das ebenfalls zweimal gedreht wird. Dieses hat ebenfalls mehrere Sektoren, von denen einige mit 5 und die anderen mit 2 beschriftet sind.
Durch Änderung der Größen der Sektoren kann jedoch die Wahrscheinlichkeit 
dafür, beim einmaligen Drehen die Zahl 5 zu erzielen, variiert werden. Der Rabatt, der einer Person beim nächsten Einkauf gewährt wird, wird auf gleiche Weise wie bisher ermittelt.
Bestimme die Wahrscheinlichkeit 
wenn beim Glückspiel mit dem Glücksrad auf lange Sicht im Mittel ein Rabatt von 
erzielt werden soll.
(4 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
Die Wahrscheinlichkeit dafür, dass eine zufällig ausgewählte Person ein Morgenkunde und kein Treuekunde ist, beträgt 
1.2
| Gesamt | |||
|---|---|---|---|
| Gesamt |
1.3
1.4
Die Wahrscheinlichkeit, dass eine zufällig ausgewählte Person sowohl ein Morgenkunde als auch ein Treuekunde ist, ergibt sich aus der Vierfeldertafel als 
Für das Produkt der Wahrscheinlichkeiten 
und 
folgt:
![\(\begin{array}[t]{rll}
P(T)\cdot P(M)&=&0,6\cdot0,2 \\[5pt]
&=&0,12
\end{array}\)](https://mathjax.schullv.de/d95afcd601e735c8295849b5eac9d11af1055e12f299c5e1c559453459237bc8?color=5a5a5a)
Da somit 
gilt, sind die Ereignisse und nicht stochastisch unabhängig.
2.1
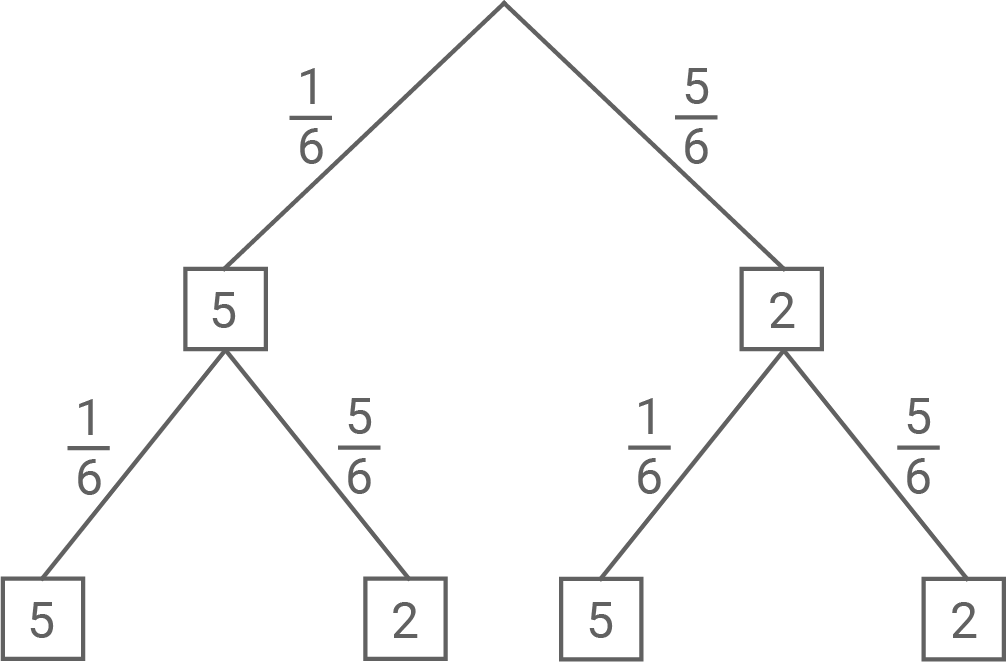
2.2
Es gibt bei sieben Plätzen vier unterschiedliche Möglichkeiten, vier Personen unmittelbar hintereinander zu verteilen. Somit folgt für die gesuchte Wahrscheinlichkeit:
2.3
Für den Erwartungswert des neuen Glücksrads soll gelten:
Mit dem solve-Befehl des CAS folgt:
