C2.1 - Stochastik

Zu einem bestimmten Zeitpunkt wird ein Spielcasino von insgesamt 80 Gästen besucht. Alle Gäste spielen entweder an einem Spieltisch oder an einem Automaten. 32 Gäste sind jünger als 45 Jahre. $37,5\;\%$ der Gäste, die jünger als 45 Jahre sind, und zwei Drittel der restlichen Gäste spielen an einem Automaten.

Ein Gast wird zufällig ausgewählt. Betrachtet werden folgende Ereignisse:

$J:$ Der Gast ist jünger als 45 Jahre.

$A:$ Der Gast spielt an einem Automaten.

1.1

Stelle den beschriebenen Sachzusammenhang in einem Baumdiagramm dar.

(3 BE)

1.2

Beschreibe das Ereignis $J \cap \overline{A}$ im Sachzusammenhang.

(2 BE)

1.3

Zeige durch eine geeignete Rechnung, dass insgesamt $55 \;\%$ der Gäste an einem Automaten spielen.

(2 BE)

1.4

Berechne, welcher Anteil der an einem Automaten spielenden Gäste jünger als 45 Jahre ist.

(2 BE)

1.5

Untersuche die Ereignisse $J$ und $A$ auf stochastische Unabhängigkeit.

(3 BE)

Bei einem der in diesem Spielcasino angebotenen Glücksspiele wird mit drei fairen Würfeln gespielt. Diese sind jeweils mit den Zahlen 1, 2, 3, 4, 5 und 6 beschriftet. Sie werden gleichzeitig geworfen.

Der Spieler legt die Höhe seines Einsatzes fest und wählt eine der sechs Zahlen als Gewinnzahl aus. Fällt die Gewinnzahl mindestens einmal, so erhält der Spieler seinen Einsatz zurück. Zusätzlich dazu erhält er einen Gewinn.

Der Gewinn entspricht dem Produkt der Anzahl der Würfel, welche die ausgewählte Gewinnzahl zeigen, und dem festgelegten Einsatz. Fällt die Gewinnzahl nicht, so verliert der Spieler seinen Einsatz.

2.1

Ein Spieler setzt einen Einsatz von $10 \;€$ und wählt die Gewinnzahl „4“.

Erläutere, weshalb er mit einer Wahrscheinlichkeit von $\dfrac{25}{72}$ nach einmaligem Spielen $20 \;€$ erhält.

(3 BE)

2.2

Ein anderer Spieler setzt ebenfalls einen Einsatz von $10 \;€$ und wählt eine Gewinnzahl.

Erläutere die Bedeutung der Summanden sowie des Ergebnisses der Rechnung $\dfrac{25}{72} \cdot 20+\dfrac{5}{72} \cdot 30+\dfrac{1}{216} \cdot 40=\dfrac{995}{108} \approx 9,21$ im Sachzusammenhang.

(5 BE)

Die Abbildung 1 zeigt das Netz eines Würfels.

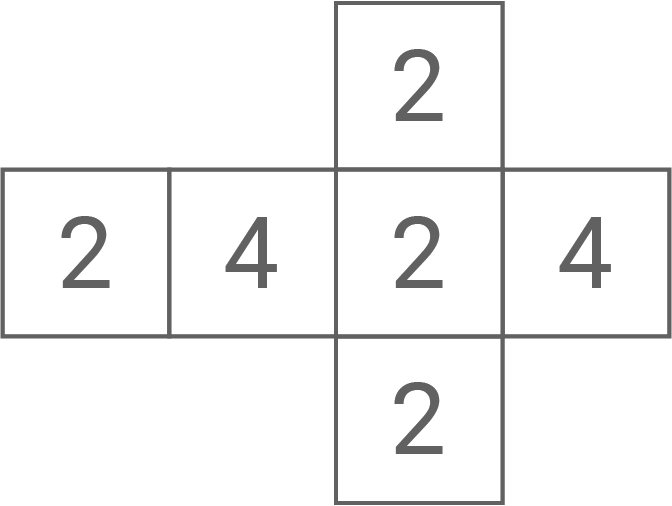
Abbildung 1

3.1

Der Würfel wird 30-mal geworfen. Die Zufallsgröße $X$ gibt an, wie oft die Zahl „4“ erzielt wird.

3.1.1

Begründe, dass $X$ binomialverteilt mit dem Parameter $p=\dfrac{1}{3}$ ist.

(2 BE)

3.1.2

Ermittle die Wahrscheinlichkeit dafür, dass die Zahl „4“ häufiger erzielt wird als die Zahl „2“.

(2 BE)

3.1.3

Gib im Sachzusammenhang ein Ereignis an, dessen Wahrscheinlichkeit mit dem Term $\pmatrix{29\\8}\cdot \left(\dfrac{1}{3}\right)^8\cdot \left(\dfrac{2}{3}\right)^{21}\cdot \dfrac{1}{3}$ berechnet werden kann.

(2 BE)

3.1.4

Bestimme den Erwartungswert für die Summe der erzielten Zahlen.

(3 BE)

3.2

Zwei Personen werfen den Würfel abwechselnd so lange, bis eine Person mit einem Wurf eine andere Zahl erzielt als die andere Person beim unmittelbar vorhergehenden Wurf.

Die Person, die dabei die größere Zahl erzielt hat, gewinnt das Spiel.

3.2.1

Begründe, dass mit dem Term $1-\left(\dfrac{1}{3}\right)^3-\left(\dfrac{2}{3}\right)^3$ die Wahrscheinlichkeit dafür berechnet werden kann, dass das Spiel spätestens mit dem dritten Wurf entschieden wird.

(2 BE)

3.2.2

Eine der beiden Personen beginnt das Spiel.

Bestimme die Wahrscheinlichkeit dafür, dass diese Person verliert und der Würfel höchstens viermal geworfen wird.

(3 BE)

Die Abbildung 2 zeigt das Netz eines weiteren Würfels.

Der Würfel wird 7500-mal geworfen. Bei den ersten 1500 Würfen wird 735-mal die Zahl „1“ und 285-mal die Zahl „6“ erzielt.

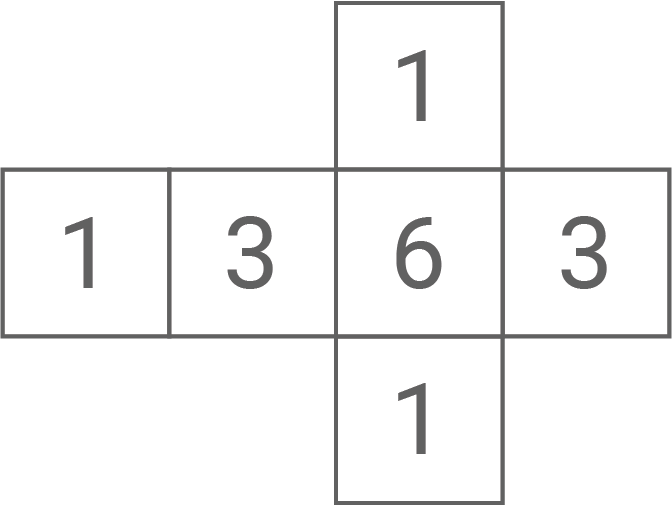
Abbildung 2

4.1

Bestimme für die ersten 1500 Würfe die relative Häufigkeit der Zahl „3“.

(2 BE)

4.2

Ermittle die Wahrscheinlichkeit dafür, dass bei höchstens $17 \; \%$ der 7500 Würfe die Zahl „6“ erzielt wird.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

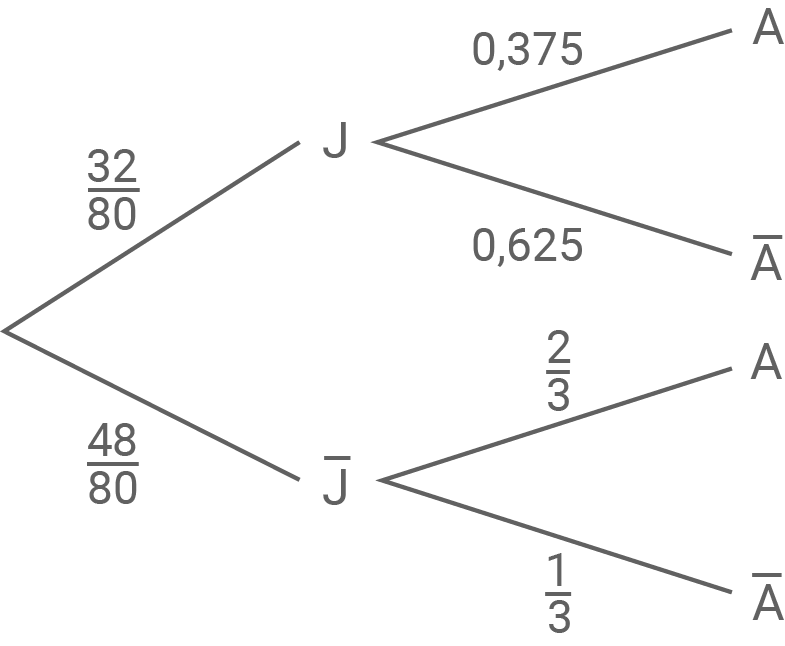
Baumdiagramm Spielcasino Automat Hessen Mathe Abi 2023

1.2

Das Ereignis $J \cap \overline{A}$ bedeutet, dass ein zufällig betrachteter Gast jünger als 45 Jahre ist und nicht am Automaten spielt.

1.3

$\begin{array}[t]{rll} P(A)&=& P(J \cap A)+P(\overline{J}\cap A)& \\[5pt] &=& \dfrac{32}{80}\cdot 0,375+\dfrac{48}{80}\cdot \dfrac{2}{3}& \\[5pt] &=& 0,55 \end{array}$

Somit spielen insgesamt $55\,\%$ der Gäste an einem Automaten.

1.4

Mit dem Satz von Bayes gilt:

$\begin{array}[t]{rll} P_A(J)&=& \dfrac{P(J)\cdot P_J(A)}{P(A)} \\[5pt] &=& \dfrac{\dfrac{32}{80}\cdot 0,375}{0,55} \\[5pt] &\approx& 0,27 \end{array}$

$27\,\%$ der an einem Automaten spielenden Gäste sind somit jünger als 45 Jahre.

1.5

Die beiden Ereignisse sind stochastisch unabhängig voneinander, wenn gilt: $P(J \cap A)= P(J) \cdot P(A)$

$\begin{array}[t]{rll} P(J \cap A)&=& \dfrac{32}{80}\cdot 0,375 & \\[5pt] &=& 0,15 \end{array}$

$\begin{array}[t]{rll} P(J)\cdot P(A)&=& \dfrac{32}{80}\cdot 0,55 & \\[5pt] &=& 0,22 \end{array}$

Somit sind die Ereignisse $J$ und $A$ nicht stochastisch unabhängig voneinander.

2.1

Der Spieler erhält genau dann $20\,€,$ wenn beim Wurf mit den drei Würfeln genau einmal die Zahl „4“ fällt.

In diesem Fall bekommt er seinen Einsatz von $10\,€$ zurück und erhält zusätzlich folgenden Gewinn:

$10\,€$

Rechenweg anzeigen

Die Wahrscheinlichkeit, dass beim gleichzeitigen Wurf von drei Würfeln genau einmal die Zahl „4“ fällt, beträgt:

$\pmatrix{3\\1}\cdot \dfrac{1}{6}\cdot \left(\dfrac{5}{6}\right)^2=\dfrac{25}{72}$

Somit erhält der Spieler mit einer Wahrscheinlichkeit von $\dfrac{25}{72}$ nach einmaligem Spielen $20\,€.$

2.2

Der Summand $\dfrac{25}{72}\cdot 20\,€$ beschreibt den Fall, dass beim Wurf mit drei Würfeln genau einmal die gewählte Gewinnzahl fällt. Dies passiert - wie in Aufgabenteil 2.1 nachgewiesen - mit einer Wahrscheinlichkeit von $\dfrac{25}{72}$ und der Spieler würde $20\,€$ erhalten.

Der Summand $\dfrac{5}{72}\cdot 30\,€$ beschreibt den Fall, dass beim Wurf mit drei Würfeln genau zweimal die gewählte Gewinnzahl fällt. Dies passiert mit einer Wahrscheinlichkeit von $\pmatrix{3\\2}\cdot \left(\dfrac{1}{6}\right)^2\cdot \dfrac{5}{6}=\dfrac{5}{72}$ und der Spieler würde $10\,€+2\cdot 10\,€=30\,€$ erhalten.

Der Summand $\dfrac{1}{216}\cdot 40\,€$ beschreibt den Fall, dass beim Wurf mit drei Würfeln genau dreimal die gewählte Gewinnzahl fällt. Dies passiert mit einer Wahrscheinlichkeit von $\pmatrix{3\\3}\cdot \left(\dfrac{1}{6}\right)^3=\dfrac{1}{216}$ und der Spieler würde $10\,€+3\cdot 10\,€=40\,€$ erhalten.

Das Ergebnis bedeutet somit, dass der Spieler nach Zahlen der $10\,€$ Einsatz nach einem Spieldurchgang eine Auszahlung von etwa $9,21\,€$ erwarten kann. Da dies weniger als sein Einsatz ist, würde mehrfaches Spielen auf Dauer somit zu Verlusten des Spielers führen.

3.1.1

Da immer der gleiche Würfel geworfen wird und die Versuche unabhängig voneinander sind, bleibt die Wahrscheinlichkeit $p$ , eine „4“ zu erzielen, stets konstant.

Durch das 30-fache Würfeln ist eine feste Anzahl an Versuchen $n$ gegeben, bei denen jeweils zwei Ergebnisse - „Es wird eine „4“ erzielt“ und „Es wird keine „4“ erzielt“ - unterschieden werden.

Somit sind alle Bedingungen für eine Binomialverteilung erfüllt.

Da $X$ angibt, wie oft die Zahl „4“ erzielt wird, und zwei der sechs Würfelflächen mit einer „4“ beschriftet sind, folgt der Parameter $p$ mit $p=\dfrac{2}{6}=\dfrac{1}{3}.$

3.1.2

$X$ beschreibt die Anzahl der Würfe, bei denen die Zahl „4“ erzielt wird, und ist binomialverteilt mit den Parametern $p=\dfrac{1}{3}$ und $n=30.$

Die Zahl „4“ muss mindestens 16-mal fallen, sodass sie häufiger als die Zahl „2“ erzielt wird.

Es gilt:

$\begin{array}[t]{rll} P(X\geq 16)&=& 1-P(X \leq 15)& \quad \scriptsize \mid CAS \\[5pt] &\approx& 1- 0,981& \\[5pt] &=& 0,019 \end{array}$

Mit einer Wahrscheinlichkeit von etwa $1,9\,\%$ wird somit die Zahl „4“ häufiger erzielt als die Zahl „2“.

3.1.3

Beim 30. Wurf wird zum neunten Mal die Zahl „4“ erzielt.

3.1.4

$\begin{array}[t]{rll} E&=& 30\cdot \left(\dfrac{1}{3}\cdot 4+\dfrac{2}{3}\cdot 2\right)&\\[5pt] &=& 80 \end{array}$

Der Erwartungswert der Summe der erzielten Zahlen beträgt somit 80.

3.2.1

Der Term $\left(\dfrac{1}{3}\right)^3$ beschreibt die Wahrscheinlichkeit dafür, dass bei den drei ersten Würfen jeweils eine „4“ erzielt wird und das Spiel somit noch nicht mit dem dritten Wurf entschieden wird.

Der Term $\left(\dfrac{2}{3}\right)^3$ beschreibt analog die Wahrscheinlichkeit dafür, dass bei den drei ersten Würfen jeweils eine „2“ erzielt wird und das Spiel somit ebenfalls noch nicht mit dem dritten Wurf entschieden wird.

Der gesamte Term gibt somit die Wahrscheinlichkeit dafür an, dass weder die Zahl „4“ noch die Zahl „2“ dreimal hintereinander fällt. Dies bedeutet, dass das Spiel spätestens mit dem dritten Wurf entschieden wird.

3.2.2

Die Person, die das Spiel beginnt, verliert das Spiel mit höchstens vier Würfen, wenn abwechselnd folgende Zahlen gewürfelt werden:

$(2,4), (2,2,2,4), (4,4,2)$

Die Wahrscheinlichkeiten hierfür betragen:

$\begin{array}[t]{rll} P(2,4)&=& \dfrac{2}{3}\cdot \dfrac{1}{3} & \\[5pt] &=& \dfrac{2}{9} \end{array}$

$\begin{array}[t]{rll} P(2,2,2,4)&=& \left(\dfrac{2}{3}\right)^3\cdot \dfrac{1}{3} & \\[5pt] &=& \dfrac{8}{81} \end{array}$

$\begin{array}[t]{rll} P(4,4,2)&=& \left(\dfrac{1}{3}\right)^2\cdot \dfrac{2}{3} & \\[5pt] &=& \dfrac{2}{27} \end{array}$

Insgesamt gilt also:

$\begin{array}[t]{rll} P(\text{Spieler 1 verliert})&=& \dfrac{2}{9}+\dfrac{8}{81}+\dfrac{2}{27}&\\[5pt] &\approx & 0,395 \end{array}$

Die Person, die das Spiel beginnt, verliert folglich mit einer Wahrscheinlichkeit von $39,5\,\%$ nach höchstens vier Würfen.

4.1

Die Zahl „3“ wird bei den ersten 1500 Würfen genau $1500-735-285=480$ -mal erzielt.

Es gilt also:

Rechenweg anzeigen

$\text{relative Häufigkeit}=0,32$

Die relative Häufigkeit der Zahl „3“ beträgt somit $32\,\%.$

4.2

Es gilt:

$0,17\cdot 7500=1275$

$X$ beschreibt die Anzahl der Würfe, bei denen die Zahl „6“ erzielt wird, und kann als binomialverteilt mit den Parametern $p=\dfrac{1}{6}$ und $n=7500$ angenommen werden.

Die Wahrscheinlichkeit, dass bei höchstens 1275 Würfen die Zahl „6“ erzielt wird, folgt also mit:

$P(X\leq 1275) \approx 0,786$

Mit einer Wahrscheinlichkeit von etwa $78,6\,\%$ wird somit bei höchstens $17 \,\%$ der 7500 Würfe die Zahl „6“ erzielt.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?