B2 - Analysis

In einem Labor wird das Wachstum einer Population von Mikroorganismen untersucht. Die Anzahl der Mikroorganismen (in Hundert) wird in Abhängigkeit von der Zeit $t$ (in Tagen nach Beobachtungsbeginn) protokolliert. In der folgenden Tabelle sind diese Werte dargestellt.

Zeit $\color{#fff}{t}$ in Tagen	Anzahl in Hundert
3	0,2
5	0,6
8	2,4
10	5,4
12	10,0
15	16,4
17	18,5
19	19,4

Stelle die Datenpaare der Tabelle in einem geeigneten Koordinatensystem grafisch dar und beschreibe den Verlauf des Bestandes der Population in den ersten 19 Tagen.

(5 BE)

Der Bestand lässt sich bis zum Ende des zwölften Tags durch eine Exponentialfunktion $f$ der Form $f(t)= a\cdot \mathrm e^{k\cdot t}$ modellieren. Hierbei gibt $f(t)$ die Anzahl der Mikroorganismen (in Hundert) und $t$ die Zeit (in Tagen nach Beobachtungsbeginn) an.

2.1

Berechne mithilfe der Datenpaare der Tabelle für $t=5$ und $t=12$ eine Funktionsgleichung der Funktion $f$ .
$\bigg[$ zur Kontrolle: $f(t) \approx 0,080 \cdot \mathrm e^{0,402 \cdot t}$ $\bigg]$

(4 BE)

2.2

Erläutere die Bedeutung des Wertes $a \approx 0,080$ im Sachzusammenhang und berechne unter Verwendung der Funktion $f$ aus Aufgabe 2.1 den prozentualen Zuwachs des Bestandes pro Tag.

(4 BE)

Ab dem Zeitpunkt $t=12$ wird der Bestand näherungsweise mithilfe der Funktion $g$ mit $g(t)=20-b \cdot \mathrm e^{c \cdot t } ( b , c \in R )$ modelliert. Hierbei gibt $g ( t )$ die Anzahl der Mikroorganismen (in Hundert) und $t$ die Zeit (in Tagen nach Beobachtungsbeginn) an.
Bestimme die Parameter $b$ und $c$ so, dass die Graphen von $f$ und $g$ an der Stelle $t =12$ ohne Sprung und ohne Knick ineinander übergehen.

(6 BE)

Über den gesamten Beobachtungszeitraum kann die Anzahl der Mikroorganismen (in Hundert) in Abhängigkeit von der Zeit $t$ (in Tagen nach Beobachtungsbeginn) mithilfe der Funktion $h$ mit $h(t)=\dfrac{100}{5+ \mathrm e ^{-0,5 \cdot t +7,6}}$ modelliert werden.

4.1

Prüfe unter Verwendung der Wertetabelle von $h$ aus dem Material, ob die Funktion $h$ zur Modellierung des Bestandes geeignet ist.

$t$	$h(t)$
3	0,22
4	0,36
5	0,59
6	0,96
7	1,53
8	2,40
9	3,68
10	5,42
11	7,60

$t$	$h(t)$
12	10,05
13	12,49
14	14,66
15	16,38
16	17,64
17	18,50
18	19,06
19	19,42

Material

(2 BE)

4.2

Bestimme den Zeitraum, in dem die Wachstumsrate der Mikroorganismen größer oder gleich 200 Mikroorganismen pro Tag beträgt.

(4 BE)

4.3

Der Inhalt der Fläche, die der Graph von $h$ mit der $t$ -Achse im Intervall $[3 ; 19]$ einschließt, soll näherungsweise bestimmt werden. Im Folgenden bezeichne $O _4$ die Obersumme bei Unterteilung des Intervalls in vier Abschnitte gleicher Breite, $U_4$ die entsprechende Untersumme. Zur Berechnung des Näherungswerts für den Inhalt der Fläche soll der folgende Ansatz verwendet werden:

$A _4=\dfrac{ O _4+ U _4}{2}$

Erläutere den Ansatz zur Berechnung von $A_4$ und bestimme das Ergebnis rechnerisch.

(5 BE)

4.4

Berechne den Zeitpunkt, ab dem die Anzahl der Mikroorganismen (in Hundert) gemäß der Modellierung mit der Funktion $h$ den Wert $17$ übersteigt.

(4 BE)

4.5

Bestimme den Inhalt der Fläche, die der Graph von $h$ mit der $t$ -Achse im Intervall $[3;19]$ einschließt.
Nenne eine Möglichkeit, den Flächeninhalt durch Veränderung des Ansatzes aus Aufgabe 4.3 besser anzunähern.

(3 BE)

4.6

Der Grenzwert von $h$ für $t \rightarrow \infty$ beträgt 20. Begründe diesen Wert anhand des Funktionsterms und erläutere die Bedeutung dieses Wertes im Sachzusammenhang.

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

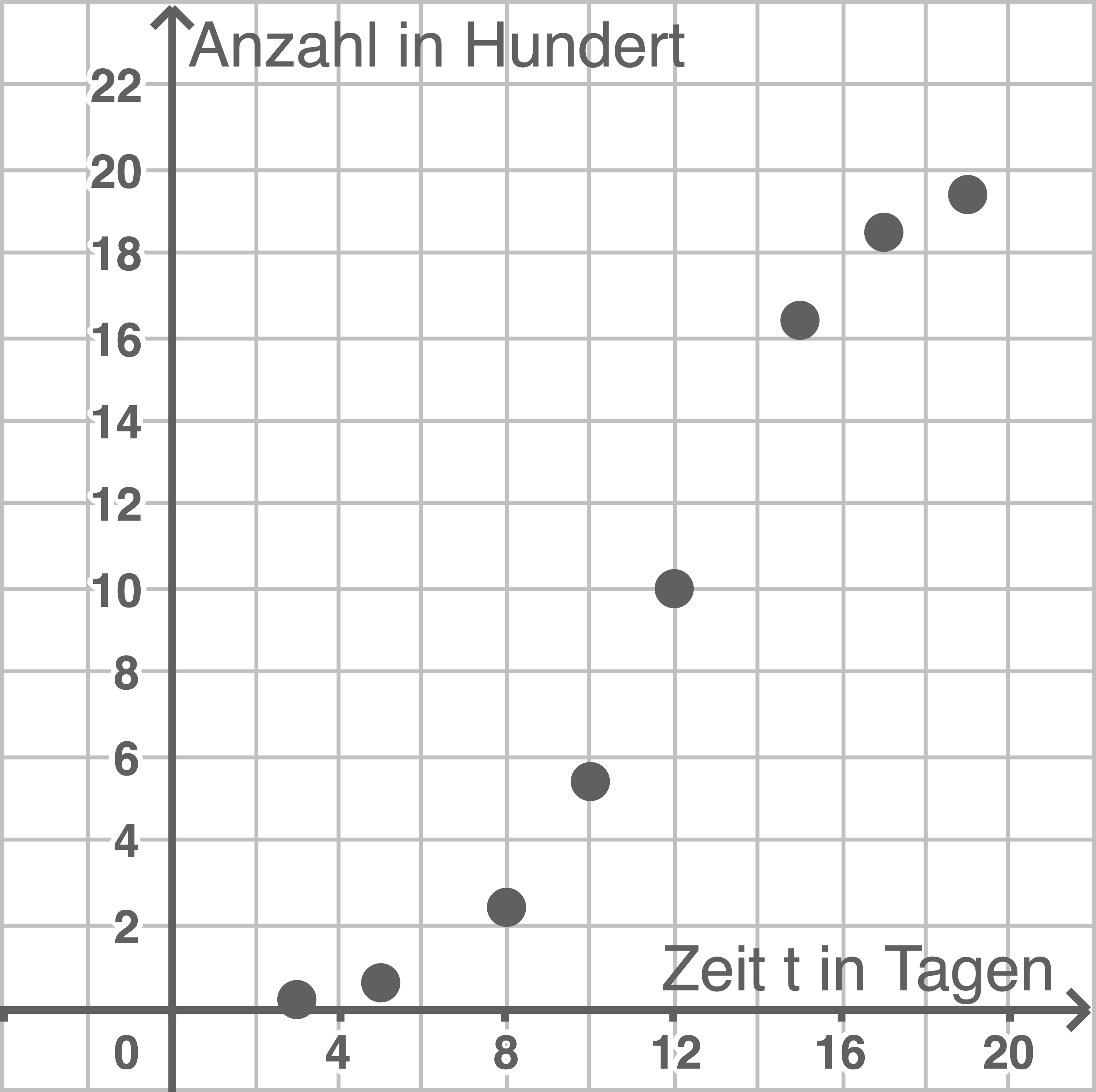
Grafische Darstellung der Datenpaare

Das Wachstum der Population in den ersten 19 Tagen ähnelt einem logistischen Verlauf.

2.1

1. Schritt: Datenpaar für $t=5$ einsetzen

$\begin{array}[t]{rll} f(5)&=& 0,6 & \\[5pt] a\cdot \mathrm e^{k\cdot 5}&=& 0,6 &\quad \scriptsize \mid\; :\mathrm e^{k\cdot 5}\\[5pt] a&=& \dfrac{0,6}{\mathrm e^{k\cdot 5}} &\\[5pt] \end{array}$

2. Schritt: Datenpaar für $t=12$ einsetzen

$\begin{array}[t]{rll} f(12)&=& 10 & \\[5pt] \dfrac{0,6}{\mathrm e^{k\cdot 5}} \cdot \mathrm e^{k\cdot 12}&=& 10 &\\[5pt] 0,6\cdot \mathrm e^{k\cdot 7}&=& 10&\quad \scriptsize \mid\; :0,6\\[5pt] \mathrm e^{k\cdot 7}&=& \dfrac{10}{0,6}&\quad \scriptsize \mid\; \ln\\[5pt] k&\approx& 0,402&\\[5pt] \end{array}$

3. Schritt: Wert von $a$ berechnen

Mit dem CAS ergibt sich: $a= \dfrac{0,6}{\mathrm e^{0,402\cdot 5}}\approx 0,080$

Somit ist eine Funktionsgleichung von $f$ gegeben durch $f(t)=0,080\cdot \mathrm e^{0,402\cdot t}.$

2.2

Bedeutung des Werts von $a$

Der Wert von $a$ gibt den Anfangsbestand der Mikroorganismen an. Für $a=0,080$ waren folglich zu Beobachtungsbeginn $8$ Mikroorganismen vorhanden.

Prozentualen Zuwachs berechnen

Es ist $f(0)= 0,080$ und $f(1)\approx 0,12.$

$\dfrac{0,12}{0,080} =1,5$

Es ist $f(11)\approx 6,65$ und $f(12)\approx 9,96.$

$\dfrac{9,96}{6,65} \approx 1,49$

Der Bestand nimmt pro Tag etwa 50% zu.

Die Graphen von $f$ und $g$ gehen genau dann an der Stelle $t=12$ ohne Sprung und ohne Knick ineinander über, wenn sie an dieser Stelle sowohl den gleichen Funktionswert als auch die gleiche Steigung besitzen.

$f(12)=0,080\cdot \mathrm e^{0,402\cdot 12}\approx 9,957$

$\begin{array}[t]{rll} g(12)&=& 9,957 & \\[5pt] 20-b\cdot \mathrm e^{c\cdot 12}&=& 9,957 & \\[5pt] \end{array}$

Mit dem solve Befehl des CAS folgt: $c= \dfrac{1}{12} \ln\left(\dfrac{10,043}{b}\right)$

Einsetzen von $c$ in die zweite Bedingung:

Rechenweg anzeigen

Mit dem solve-Befehl des CAS ergibt sich $b\approx 1255,375.$

Es folgen somit $b=1255,375$ und $c=\dfrac{1}{12}\ln\left(\dfrac{10,043}{1255,375}\right)\approx -0,402.$

4.1

Die Funktion $h$ ist zur Modellierung des Bestands geeignet, da die Werte in der Tabelle bis zum Zeitpunkt $t=12$ immer schneller wachsen und der Zuwachs anschließend wieder abnimmt.

Zudem stimmen die Datenpaare der Wertetabelle von $h$ gerundet mit den Werten der Tabelle aus 1 überein.

4.2

Die Wachstumsrate entspricht der ersten Ableitung $\(h$

Mit dem CAS kann diese grafisch dargestellt werden.

Der Zeitraum, in welchem der Graph der Ableitungsfunktion größer oder gleich $200$ ist, kann abgelesen werden.

Es ergibt sich das Intervall $I[4,5;20]$

4.3

Ansatz erläutern

Die Obersumme beschreibt den Flächeninhalt des jeweiligen Intervalls anhand des darin größten Funktionswerts und ist somit größer als der tatsächliche Flächeninhalt des Intervalls.

Bei der Untersumme wird der Inhalt durch den jeweils kleinsten Funktionswert des Intervalls berechnet, diese ist folglich kleiner als der tatsächliche Flächeninhalt.

Der Durchschnitt der Ober- und Untersumme nähert sich somit an den tatsächlichen Flächeninhalt an.

1. Schritt: Obersumme berechnen

Das Intervall $[3;19]$ wird in 4 gleich große Intervalle geteilt:

$I_1[3;7], I_2[7;11],I_3[11;15],I_4[15;19]$

Da $h$ monoton steigt, besitzt jeweils die rechte Intervallgrenze den größten Funkionswert.

Rechenweg anzeigen

$O_4 = 179,72$

2. Schritt: Untersumme berechnen

Rechenweg anzeigen

$U_4=102,92$

3. Schritt: Flächeninhalt berechnen

$A_4=\dfrac{179,72+102,92}{2}=141,32$

4.4

$\begin{array}[t]{rll} h(t)&=& 17 & \\[5pt] \dfrac{100}{5+ \mathrm e^{-0,5 \cdot t+7,6}}&=& 17 \end{array}$

Mit dem solve-Befehl des CAS ergibt sich $t \approx 15,45.$

Ab dem Zeitpunkt $t=15,45$ übersteigt die Anzahl der Mikroorganismen gemäß der Modellierung mit Funktion $h$ den Wert $17.$

4.5

Flächeninhalt der eingeschlossenen Fläche bestimmen

Es gilt $A= \displaystyle\int_{3}^{19}h(t)\;\mathrm dt$

Mit dem CAS ergibt sich: $A\approx 141,11$

Ansatz aus 4.3 verändern

Durch das Unterteilen des Intervalls in mehr als 4 Intervalle kann der Flächeninhalt besser angenähert werden.

Umso kleinere Intervalle, desto genauer das Ergebnis.

4.6

Für $t\rightarrow\infty$ gilt $\mathrm e^{-0,5 \cdot t+7,6}\rightarrow 0$ und somit folgt:

$\lim\limits_{t\to\infty} h(t)= \dfrac{100}{5+0}=20$

Dieser Grenzwert bedeutet, dass der Bestand der Mikroorganismen auf Dauer nie über eine Anzahl von $2000$ Mikroorganismen steigen wird.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?