C2.2 - Stochastik

In einer Bäckerei werden handgemachte Berliner (ein Süßgebäck) hergestellt. In einer Tagesproduktion sind $60\,\%$ der Berliner mit Marmelade gefüllt, der Rest ist ungefüllt. $25\,\%$ der mit Marmelade gefüllten Berliner und $50\,\%$ der nicht mit Marmelade gefüllten Berliner sind mit Zuckerguss überzogen, die übrigen sind mit Puderzucker bestreut.

Betrachtet werden folgende Ereignisse:

$M:$ Der Berliner ist mit Marmelade gefüllt.

$Z:$ Der Berliner ist mit Zuckerguss überzogen.

1.1

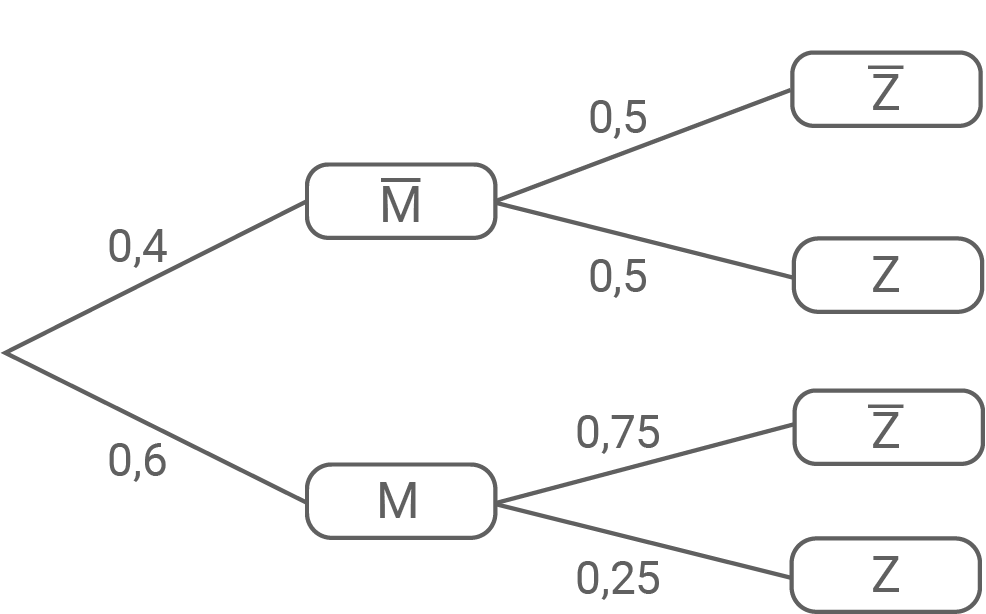
Stelle den beschriebenen Sachzusammenhang in einem Baumdiagramm dar.

(3 BE)

1.2

Beschreibe die Bedeutung des Terms $P(M\cap Z)$ im Sachzusammenhang und berechne den entsprechenden Wert.

(3 BE)

1.3

Zeige rechnerisch, dass insgesamt $35\,\%$ der Berliner mit Zuckerguss überzogen sind.

(2 BE)

1.4

Berechne, welcher Anteil der mit Zuckerguss überzogenen Berliner mit Marmelade gefüllt ist.

(2 BE)

1.5

Es werden aus der Tagesproduktion 10 Berliner zufällig ausgewählt und überprüft, ob sie mit Marmelade gefüllt sind. Es kann davon ausgegangen werden, dass es sich bei diesem Zufallsexperiment um eine Bernoulli-Kette handelt.

1.5.1

Erörtere, welchen Einfluss die Gesamtzahl der Berliner in der Tagesproduktion auf die Modellierung des Sachzusammenhangs mit einer Bernoulli-Kette hat.

(3 BE)

1.5.2

Beschreibe im gegebenen Sachzusammenhang ein Ereignis $E,$ für das gilt:

Formel anzeigen

$P(E) = \dots$

und gib die Wahrscheinlichkeit $P(E)$ an.

(3 BE)

1.5.3

Bestimme die Wahrscheinlichkeit der folgenden Ereignisse.

$G:$ Genau 6 Berliner sind mit Marmelade gefüllt.

$H:$ Mindestens 8 Berliner sind mit Marmelade gefüllt.

$I:$ Die Anzahl der mit Marmelade gefüllten Berliner weicht um höchstens 2 vom Erwartungswert ab.

(8 BE)

Zwei Mitarbeiter stellen jeweils 50 Berliner von Hand her und bestimmen deren Gewicht mit einer auf Gramm genauen Waage. Die Ergebnisse sind im Folgenden dargestellt.

Untersuchung des Gewichts der Berliner

Mitarbeiter $A:$

Gewicht in Gramm	Anzahl der Berliner
$88$	$6$
$89$	$9$
$90$	$10$
$91$	$12$
$92$	$8$
$93$	$5$

Mitarbeiter $B:$

Gewicht in Gramm	Anzahl der Berliner
$88$	$2$
$89$	$5$
$90$	$20$
$91$	$16$
$92$	$6$
$93$	$1$

2.1

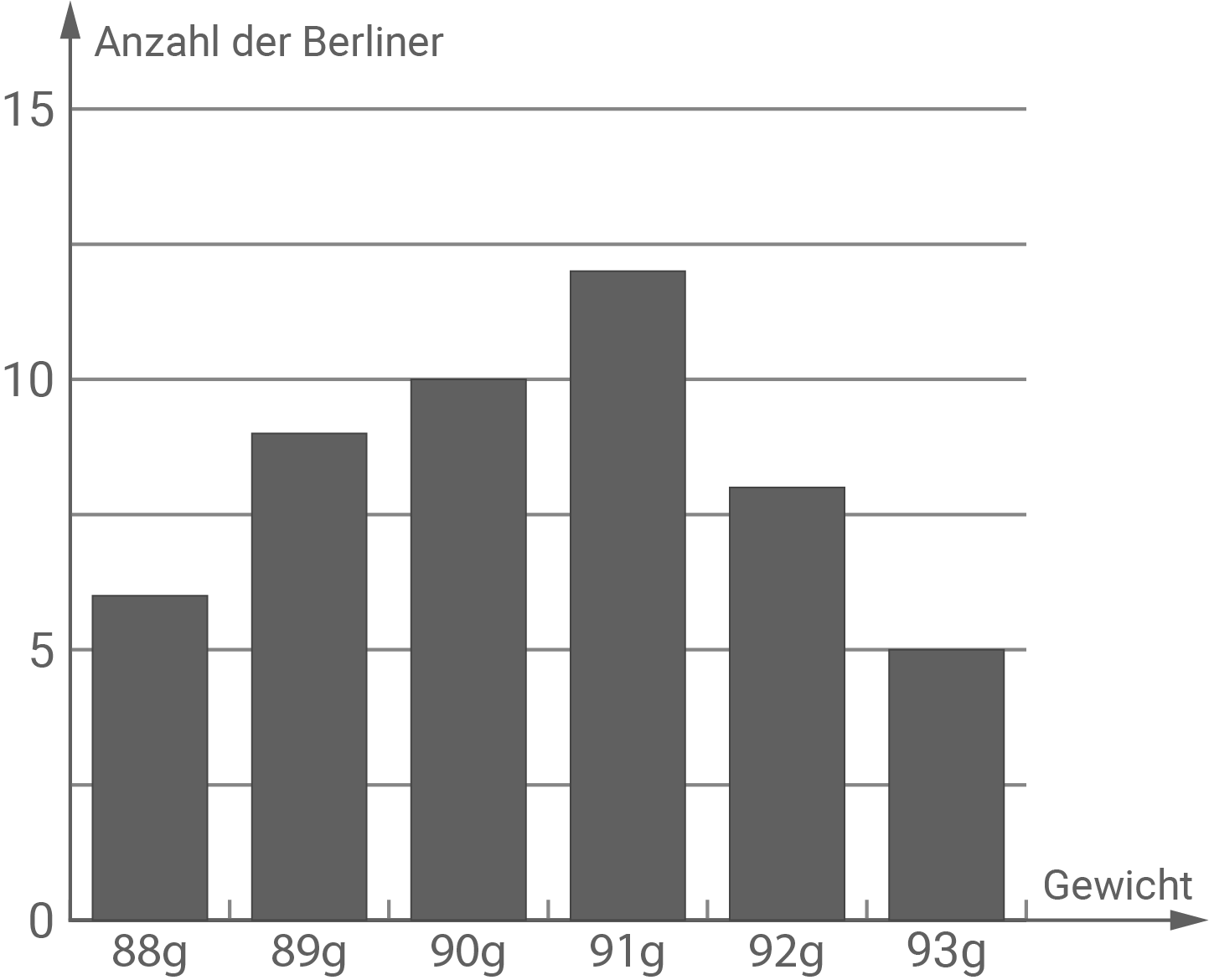
Stelle die Daten von Mitarbeiter $A$ graphisch in einem Diagramm dar.

(5 BE)

2.2

Zeige rechnerisch, dass der arithmetische Mittelwert des Gewichts der Berliner bei beiden Mitarbeitern jeweils gleich groß ist.

(4 BE)

2.3

Erörtere ohne weitere Rechnung, bei welchem der beiden Mitarbeiter die (empirische) Standardabweichung des Gewichts größer ist.

(3 BE)

Beim Bezahlen an der Kasse bietet die Bäckerei bei einer Rabattaktion zwei Varianten an:

Variante 1:

Der Kunde erhält $3\,\%$ Rabatt auf den Einkauf.

Variante 2:

Es wird mit zwei herkömmlichen Spielwürfeln gewürfelt, die jeweils mit den Zahlen 1, 2, 3, 4, 5 und 6 beschriftet sind. Fallen dabei zwei Sechsen, bekommt der Kunde seinen Einkauf geschenkt. Andernfalls muss er den vollen Preis bezahlen.

Untersuche, welche Variante langfristig für den Kunden günstiger ist.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

1.2

$P(M \cap Z)$ beschreibt den Anteil an Berlinern, die mit Marmelade befüllt und mit Zuckerguss überzogen sind.

Mit der Pfadmultiplikationsregel folgt:

$P(M \cap Z) = 0,6 \cdot 0,25 = 0,15$

Der Anteil der mit Marmelade befüllten und mit Zuckerguss überzogenen Berlinern beträgt somit $15 \%.$

1.3

Sei $Z$ die Anzahl der mit Zuckerguss überzogenen Berliner. Dann gilt nach der Pfadmultiplikationsregel:

$\begin{array}[t]{rll} P(Z)&=& 0,6 \cdot 0,25 + 0,4 \cdot 0,5 & \\[5pt] &=& 0,35 \end{array}$

Damit sind insgesamt $35 \%$ der Berliner mit Zuckerguss überzogen.

1.4

Für den Anteil gilt:

$\begin{array}[t]{rll} P_Z(M)&=& \dfrac{P(M)\cdot P_M(Z)}{P(Z)}& \\[5pt] &=& \dfrac{0,6 \cdot 0,25}{0,25\cdot 0,6+0,5\cdot 0,4} & \\[5pt] &\approx& 0,4286 & \\[5pt] \end{array}$

Damit sind ca. $42,86 \%$ der mit Zuckerguss überzogenen Berliner mit Marmelade gefüllt.

1.5

1.5.1

Die Gesamtzahl der Berliner in der Tagesproduktion hat Einfluss auf die Genauigkeit der Modellierung des Sachzusammenhangs mit einer Bernoulli-Kette.

Je mehr Berliner in einer Tagesproduktion produziert werden, desto genauer wird die Modellierung. Das liegt daran, dass sich die prozentuale Verteilung des Berliner-Angebots bei Wegnahme eines Berliners weniger verändert, je mehr Berliner zur Verfügung stehen.

1.5.2

Untersuchung der einzelnen Komponenten von $P(E):$

Aufteilung anzeigen

$D_{1}: \; 0,4^{10} = \pmatrix{10\\0} \cdot 0,6^{0} \cdot 0,4^{10}$
Dies entspricht der Wahrscheinlichkeit, dass 0 der 10 getesteten Berliner mit Marmelade gefüllt sind.

$D_{2}:\; 10\cdot 0,6\cdot 0,4^9$ $= \pmatrix{10\\1} \cdot 0,6^{1} \cdot 0,4^{9}$
Dies entspricht der Wahrscheinlichkeit, dass einer der 10 getesteten Berliner mit Marmelade gefüllt ist.

$D_{3}: \; \pmatrix{10\\2}\cdot 0,6^2\cdot 0,4^8$
Dies entspricht der Wahrscheinlichkeit, dass 2 der 10 getesteten Berliner mit Marmelade gefüllt sind.

$D_{4}:\; \pmatrix{10\\3}\cdot 0,6^3\cdot 0,4^7$
Dies entspricht der Wahrscheinlichkeit, dass 3 der 10 getesteten Berliner mit Marmelade gefüllt sind.

Deutung des Terms

$P(E)$ beschreibt somit die Wahrscheinlichkeit, dass entweder 0, 1, 2 oder 3 der 10 Berliner mit Marmelade gefüllt sind.

Wahrscheinlichkeit berechnen

Mit dem WTR ergibt sich:

$P(E) \approx 0,055 =5,5 \,\%$

1.5.3

Die Zufallsvariable $X$ beschreibt die Anzahl der mit Marmelade gefüllten Berliner und ist $B_{10; \; 0,6}$ verteilt.

Ereignis G

$P(G) = P(X = 6) \approx 0,2508$

Die Wahrscheinlichkeit für das Ereignis $G$ beträgt ca. $25,08 \%.$

Ereignis H

$\begin{array}[t]{rll} P(H)&=& P(X \geq 8)& \\[5pt] &=& 1 - P(X \leq 7) & \\[5pt] &\approx& 0,1673 \end{array}$

Die Wahrscheinlichkeit für das Ereignis $H$ beträgt ca. $16,73\%.$

Ereignis I

$\begin{array}[t]{rll} P(I)&=& P(4 \leq X \leq 8)& \\[5pt] &=& P(X \leq 8) - P(X \leq 3)& \\[5pt] &\approx& 0,8988 \end{array}$

Die Wahrscheinlichkeit für das Ereignis $I$ beträgt ca. $89,88 \%.$

2.1

2.2

Für das arithmetische Mittel bei Mitarbeiter $A$ gilt:

Rechnung anzeigen

Für das arithmetische Mittel bei Mitarbeiter $B$ gilt:

Rechnung anzeigen

Damit ist der arithmetische Mittelwert des Gewichts der Berliner bei beiden Mitarbeitern jeweils gleich groß.

2.3

Bei Mitarbeiter $B$ wiegt der Großteil der Berliner $90 \, \text{g}$ oder $91 \, \text{g} \,$ , wohingegen die Berliner von Mitarbeiter $A$ recht gleichmäßig auf die verschiedenen Gewichtsklassen verteilt sind. Damit ist die Standardabweichung des Mitarbeiters $A$ größer als die des Mitarbeiters $B.$

Variante 1:

Es wird langfristig $3\,\%$ Rabatt auf den Einkaufpreis erwartet.

Variante 2:

Langfristiger Erwartungswert für den Rabatt:

$\begin{array}[t]{rll} E(X)&=& \dfrac{1}{6} \cdot \dfrac{1}{6} \cdot 1 + \left(1 - \dfrac{1}{6} \cdot \dfrac{1}{6}\right) \cdot 0 & \\[5pt] &=& \dfrac{1}{36}& \\[5pt] &\approx& 0,0278 & \\[5pt] &=& 2,78 \% \end{array}$

Damit ist Variante 1 langfristig kostengünstiger als Variante 2.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?