A1 - Analysis

Die kanadische Wasserpest ist eine krautartige Wasserpflanze, die auch in hessischen Seen weit verbreitet ist.

Die Wachstumsgeschwindigkeit einer solchen Pflanze (in $\text{cm}$ /Tag) soll näherungsweise durch die Funktion $w$ mit

$\begin{array}[t]{rll} w(t)&=& \dfrac{1}{1\,350}t\cdot(t-45)^2&\\[5pt] &=& \dfrac{1}{1\,350}t^3-\dfrac{1}{15}t^2+\dfrac{3}{2}t \end{array}$

für $0\leq t\leq 45$ beschrieben werden, wobei $t$ die Zeit in Tagen nach Beobachtungsbeginn angibt.

1.1

Berechne die Nullstellen der Funktion $w$ sowie die Extrem- und Wendepunkte des Graphen von $w$ ohne Beachtung der Einschränkung des Definitionsbereichs.

(11 BE)

1.2

Zeichne den Graphen von $w$ im Intervall $[0; 45]$ in ein geeignetes Koordinatensystem.

(4 BE)

1.3

Erläutere die Bedeutung der Nullstellen und der Wendestelle von $w$ im Sachzusammenhang.

(4 BE)

1.4

Zeige unter Angabe einer Stammfunktion von $w$ , dass

$\dfrac{1}{45-15}\displaystyle\int_{15}^{45}w(t)\;\mathrm dt = w(30)$

gilt und erläutere diese Gleichung im Sachzusammenhang.

(7 BE)

Alternativ kann die Wachstumsgeschwindigkeit einer solchen Pflanze (in $\text{cm}$ /Tag) durch eine Exponentialfunktion $v$ mit

$v(t)= a\cdot t\cdot \mathrm e ^{-b\cdot t}$ $(a, b\gt 0)$ für $0 \leq t \leq 45$

beschrieben werden, wobei $t$ die Zeit in Tagen nach Beobachtungsbeginn angibt.

2.1

Erläutere die Bedeutung der Zeilen $\text{(I)}$ und $\text{(II)}$ im untenstehenden Kasten für das Wachstumsverhalten der Pflanze.

Zeilen anzeigen

(4 BE)

2.2

Bestätige rechnerisch, dass die Gleichungen $v(15) = 10$ und $\(v$ durch die Wahl der Parameter $a= \dfrac{2\mathrm e}{3}$ und $b = \dfrac{1}{15}$ erfüllt werden.

(6 BE)

Im Folgenden soll für die Funktion $v$ aus Aufgabe 2 gelten:

$a = \dfrac{2\mathrm e}{3}$ und $b = \dfrac{1}{15}$

Ein Biologe beobachtet, dass ein Spross der Pflanze, der zum Zeitpunkt $t=0$ zu wachsen beginnt, nach 45 Tagen eine Länge von $2,5 \,\text{m}$ erreicht.

Bestimme für beide Funktionen $w$ und $v$ jeweils, welche Länge sich nach 45 Tagen ergibt.

Beurteile, ob die Funktionen $w$ und $v$ hinsichtlich der Beobachtung des Biologen das Wachstum der Pflanze korrekt beschreiben.

(4 BE)

1.1

Nullstellen berechnen

Nullsetzen von $w(t)$ liefert:

$\begin{array}[t]{rll} w(t)&=& 0 \\[5pt] \dfrac{1}{1350}t\cdot(t-45)^2&=& 0 &\quad \scriptsize \mid\; \cdot 1350 \\[5pt] t\cdot(t-45)^2&=& 0 & \\[5pt] \end{array}$

Mit dem Satz vom Nullprodukt folgt $t_1=0$ und:

$\begin{array}[t]{rll} (t-45)^2&=& 0 &\quad \scriptsize \mid\; \sqrt{\;}\\[5pt] t-45&=& 0 &\quad \scriptsize \mid\; +45\\[5pt] t_2&=& 45 \end{array}$

Die Nullstellen der Funktion $w(t)$ sind somit gegeben durch $t_1 = 0$ und $t_2 = 45.$

Extrempunkte bestimmen

Für die ersten drei Ableitungen von $w(t) =\dfrac{1}{1350}t^3-\dfrac{1}{15}t^2+\dfrac{3}{2}t$ folgt:

$\(\begin{array}[t]{rll} w$

1. Schritt: Notwendige Bedingung für Extremstellen anwenden

$\(\begin{array}[t]{rll} w$

Mit der $pq$ -Formel folgt:

$\begin{array}[t]{rll} t_{1,2}&=& \dfrac{60}{2} \pm \sqrt{\left(\dfrac{-60}{2}\right)^2 -675 } \\[5pt] &=& 30 \pm 15 \\[5pt] \end{array}$

Mögliche Extremstellen sind also $t_1 = 15$ und $t_2 = 45$ .

2. Schritt: Hinreichende Bedingung für Extremstellen anwenden

$\(\begin{array}[t]{rll} w$

Der Graph von $w$ besitzt somit an der Stelle $t_1$ einen Hochpunkt und an der Stelle $t_2$ einen Tiefpunkt.

3. Schritt: Funktionswerte berechnen

$\begin{array}[t]{rll} w(t_1)&=& w(15) \\[5pt] &=&\dfrac{1}{1350}15^3-\dfrac{1}{15}15^2+\dfrac{3}{2}15 \\[5pt] &=&\dfrac{5}{2} - 15 + \dfrac{45}{2}\\[5pt] &=& 10 \end{array}$

$\begin{array}[t]{rll} w(t_2)&=& w(45) \\[5pt] &=&\dfrac{1}{1350}45^3-\dfrac{1}{15}45^2+\dfrac{3}{2}45 \\[5pt] &=&\dfrac{135}{2} - 135 + \dfrac{135}{2}\\[5pt] &=& 0 \end{array}$

Der Graph von $w$ besitzt den Hochpunkt $H(15\mid 10)$ und den Tiefpunkt $T(45\mid 0).$

Wendestellen bestimmen

1. Schritt: Notwendige Bedingung für Wendestellen anwenden

$\(\begin{array}[t]{rll} w$

Eine mögliche Wendestelle ist somit $t = 30.$

2. Schritt: Hinreichende Bedingung für Wendestellen anwenden

$\(w$

Es handelt sich bei $t=30$ somit um eine Wendestelle.

8. Schritt: Funktionswert berechnen

$\begin{array}[t]{rll} w(30)&=& \dfrac{1}{1350}30^3-\dfrac{1}{15}30^2+\dfrac{3}{2}30 \\[5pt] &=& 20 - 60 + 45\\[5pt] &=& 5 \end{array}$

Der Graph von $w$ besitzt folglich den Wendepunkt $W(30\mid 5).$

1.2

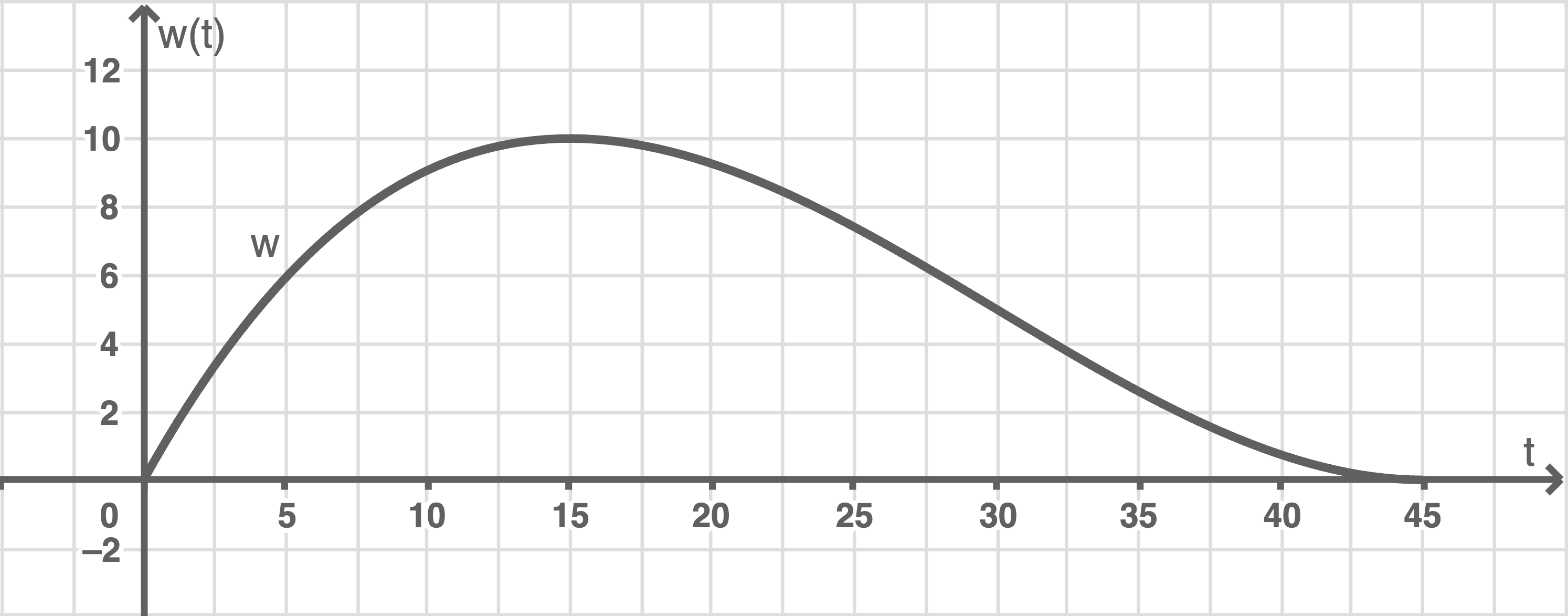
1.3

Bedeutung der Nullstellen erläutern

Die Nullstellen von der Wachstumsfunktion $w(t)$ beschreiben die Zeitpunkte, zu denen die Pflanze noch nicht bzw. nicht mehr wächst.

Bedeutung der Wendestellen erläutern

An der Wendestelle $t=30$ nimmt $w(t)$ am stärksten ab.

Somit beschreibt die Wendestelle den Zeitpunkt nach Beobachtungsbeginn, zu dem die Wachstumsgeschwindigkeit der kanadischen Wasserpest am stärksten abnimmt.

1.4

Gültigkeit der Gleichung zeigen

Stammfunktion von $w(t)$ bstimmen:

$W(t)= \dfrac{1}{5400}t^4 - \dfrac{1}{45}t^3+\dfrac{3}{4}t^2 +d$

Rechenweg anzeigen

Mit Hilfe dieser Stammfunktion und mit $d=0$ folgt für die linke Seite des Ausdrucks:

$\dfrac{1}{45-15}\displaystyle\int_{15}^{45}w(t)\;\mathrm dt =5$

Rechenweg anzeigen

Für die rechte Seite gilt:

$w(30)=5$

Rechenweg anzeigen

Da die Lösungen beider Seiten übereinstimmen, gilt die Gleichung.

Gleichung erläutern

Die linke Seite der Gleichung beschreibt den durchschnittlichen Funktionswert von $w$ im Intervall $[15;45]$ und damit die mittlere Wachstumsgeschwindigkeit zwischen dem 15. und 45. Tag nach Beobachtungsbeginn.

Die rechte Seite der Gleichung beschreibt die Wachstumsgeschwindigkeit 30 Tage nach Beobachtungsbeginn.

Die durchschnittliche Wachstumsgeschwindigkeit im Zeitraum zwischen dem 15. und 45. Tag nach Beobachtungsbeginn ist somit genauso groß wie die momentane Wachstumsgeschwindigkeit 30 Tage nach Beobachtungsbeginn.

2.1

Zeile $\boldsymbol{(\text{I})}$

Da $v(t)$ die momentane Wachstumsgeschwindigkeit $t$ Tage nach Beobachtungsbeginn beschreibt, beträgt diese 15 Tage nach Beobachtungsbeginn $10\,\text{cm/Tag}.$

Zeile $\boldsymbol{(\text{II})}$

Die Bedingungen $\(v$ und $\(v$ beschreiben ein lokales Maximum von $v(t)$ an der Stelle $t=15.$

Die Wachstumsgeschwindigkeit der Pflanze ist damit 15 Tage nach Beobachtungsbeginn am höchsten.

2.2

1. Schritt: Ableitung bestimmen

Einsetzen dervon $a=\dfrac{2\mathrm e}{3}$ und $b=\dfrac{1}{15}$ liefert:

$v(t)=\dfrac{2\mathrm e}{3}\cdot t\cdot \mathrm e^{-\frac{1}{15}\cdot t}$

Mit der Produkt- und Kettenregel ergibt sich:

$\(v$

Rechenweg anzeigen

2. Schritt: Gleichungen rechnerisch bestätigen

$\(\begin{array}[t]{rll} v(15)&=& \dfrac{2\mathrm e}{ 3} \cdot 15 \cdot \mathrm e^{-\frac{1}{15}\cdot 15} \\[5pt] &=& 10\mathrm e \cdot \mathrm e^{-1} \\[5pt] &=& 10\mathrm e \cdot \mathrm e^{-1} \\[5pt] &=& 10 \\[5pt] v$

Die Gleichungen werden also durch die Wahl der Parameter erfüllt.

Länge der Pflanze berechnen

Mit der Stammfunktion aus Aufgabe 1.4 ergibt sich:

$h_w(45) \approx 253,13 \, [\text{cm}]$

Rechenweg anzeigen

Für die Berechnung einer Stammfunktion von $v$ wird die partielle Integration verwendet:

Formel anzeigen

Mit $f(x)=\dfrac{2\mathrm e}{3}\cdot t$ und $\(g$ folgt also:

$h_v(45)\approx 326,54 \, [\text{cm}]$

Rechenweg anzeigen

Nach 45 Tagen wäre die Pflanze bei einer Modellierung mit der Funktion $w$ ca. $253,13 \,\text{cm} \approx 2,53\,\text{m}$ lang, bei einer Modellierung durch $v$ ca. $326,54 \,\text{cm} \approx 3,27 \,\text{m}$ lang.

Funktionen beurteilen

Da der Wert der Modellierung mit Hilfe der Funktion $w$ nur geringfügig von dem beobachteten Wert des Biologen abweicht, ist diese Funktion gut für die Beschreibung des Wachstums geeignet.

Bei Verwendung der Funktion $v$ ergibt sich ein deutlich zu großer Wert für die Länge.