B1 – Analysis

Zur Vorbereitung einer Marsmission plant die NASA, Flüge zum Mond durchzuführen. Eine entsprechende Rakete startet an einem bestimmten Tag um 19:00 Uhr vom Kennedy Space Center am Cape Canaveral an der Ostküste Floridas.

Die Beschleunigungsphase der Rakete nach dem Start dauert 8 Minuten.

Die Geschwindigkeit der Rakete (in Kilometer pro Minute) lässt sich in dieser Phase näherungsweise durch die Funktion $f$ mit $f(t)=-2 t^3+24 t^2$ für $0 \leq t \leq 8, \, t \in \mathbb{R},$ beschreiben, wobei $t$ die Zeit in Minuten nach dem Start der Rakete angibt.

Der Graph von $f$ ist in der Abbildung dargestellt.

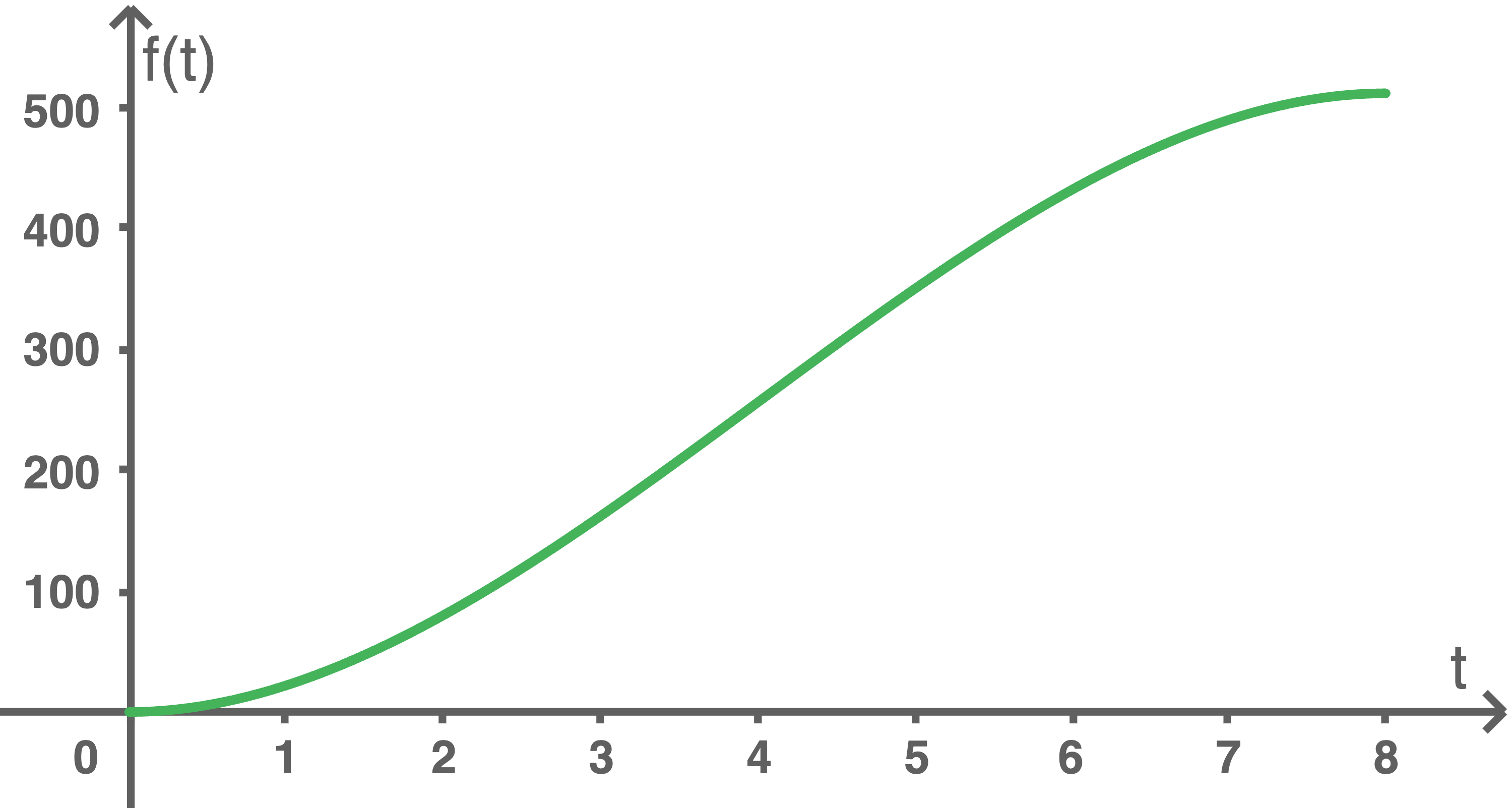
Niedersachsen Mathe Abi gA GTR 2023 Funktion f

Abbildung 1:
Geschwindigkeit der Rakete in den ersten 8 Minuten nach dem Start

1.1

Bestimme die Geschwindigkeit der Rakete am Ende der Beschleunigungsphase in der Einheit Kilometer pro Stunde.

(2 BE)

1.2

Berechne die Wendestelle von $f$ und erläutere deren Bedeutung im Sachzusammenhang.

Hinweis: Die Untersuchung der notwendigen Bedingung ist ausreichend.

(5 BE)

1.3

In der Abbildung 2 sind die Graphen der Ableitungsfunktion von $f$ und derjenigen Stammfunktion $F,$ die durch den Ursprung verläuft, im betrachteten Intervall dargestellt.

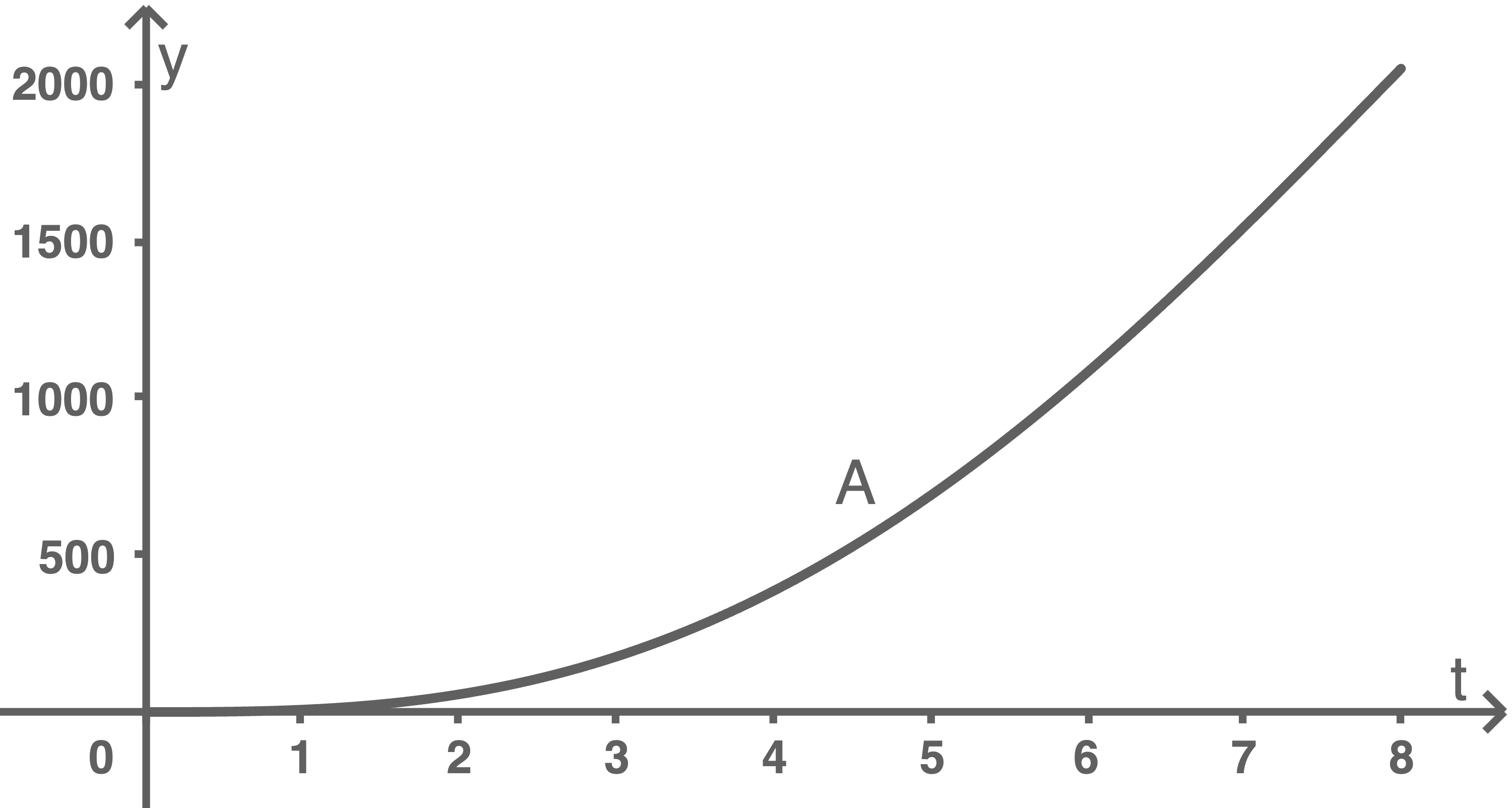
Diagramm mit einer Kurve, die einen Anstieg über die Zeit zeigt. Achsen beschriftet mit y und t.

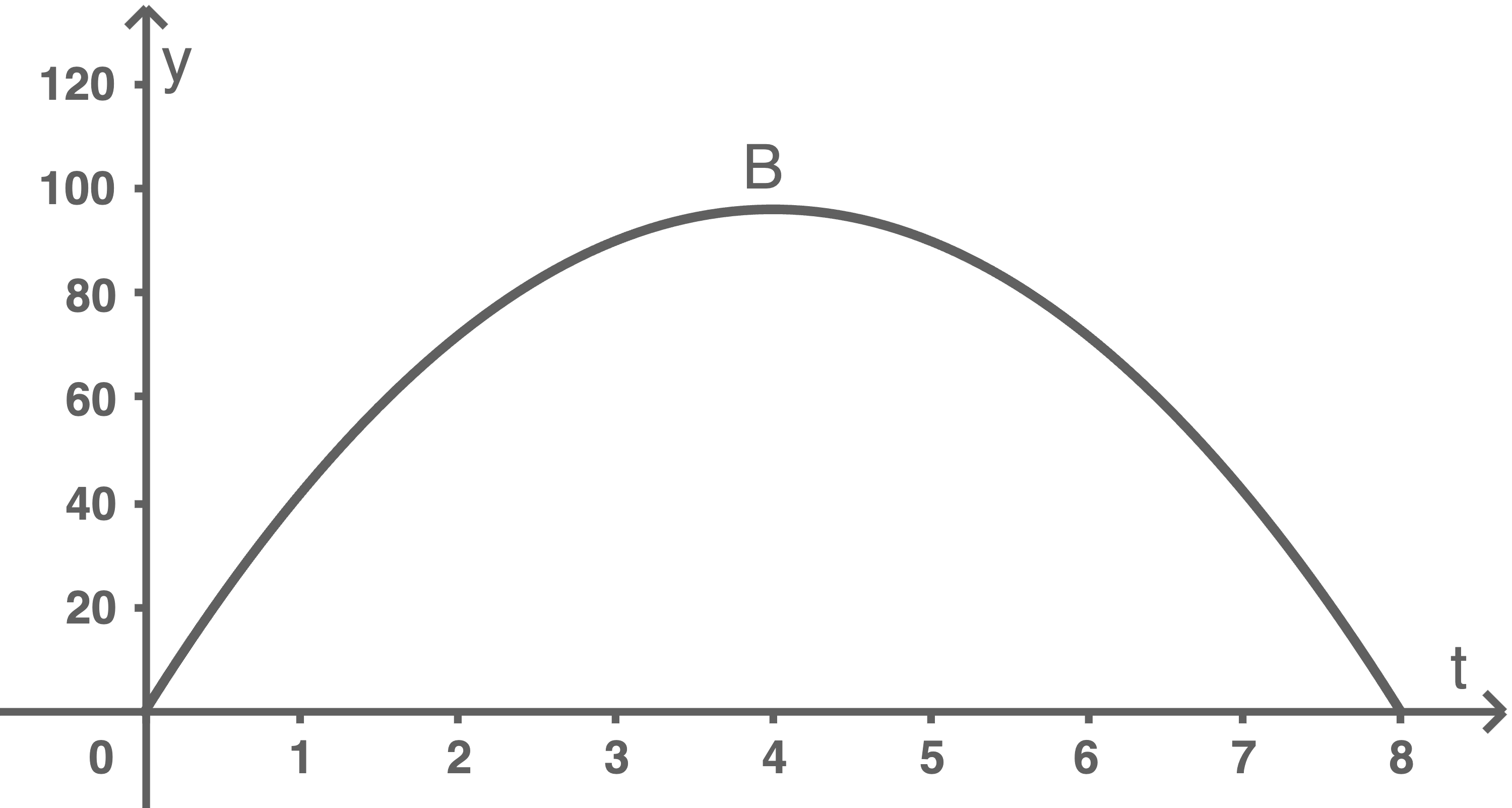Graf eines Parabelverlaufs mit Achsenbeschriftung für y und t. Punkt B markiert den höchsten Punkt.

Abbildung 2: Graphen der Ableitung und einer Stammfunktion von $f$

Begründe ohne Rechnung, welcher der beiden Graphen A und B zur Ableitungsfunktion gehört.

Beschreibe die Bedeutung der dargestellten Stammfunktion im Sachzusammenhang.

(4 BE)

1.4

Berechne den Wert des Terms $\dfrac{1}{5}\cdot \displaystyle\int_{2}^{7}f(t)\;\mathrm dt$ und deute das Ergebnis im Sachzusammenhang.

(5 BE)

Von einem bestimmten Strandabschnitt aus kann der Raketenstart sehr gut beobachtet werden.

Die Änderungsrate der Personenanzahl (in Personen pro Minute) auf diesem Strandabschnitt in den 5 Stunden vor dem Start kann in sehr guter Näherung durch die Funktion $g$ mit $g(t)=-4 t \cdot \mathrm e^{0,02 \cdot t}$ für $-300 \leq t \leq 0, \; t \in \mathbb{R},$ beschrieben werden, wobei $t$ die Zeit in Minuten angibt.

Die Rakete startet zum Zeitpunkt $\mathrm{t}=0,$ demnach ist $\mathrm{t}\lt 0$ der Zeitraum vor dem Raketenstart.

Der Graph von $g$ ist in der Abbildung 3 dargestellt. Zum Startzeitpunkt der Rakete befinden sich 10700 Personen auf dem Strandabschnitt.

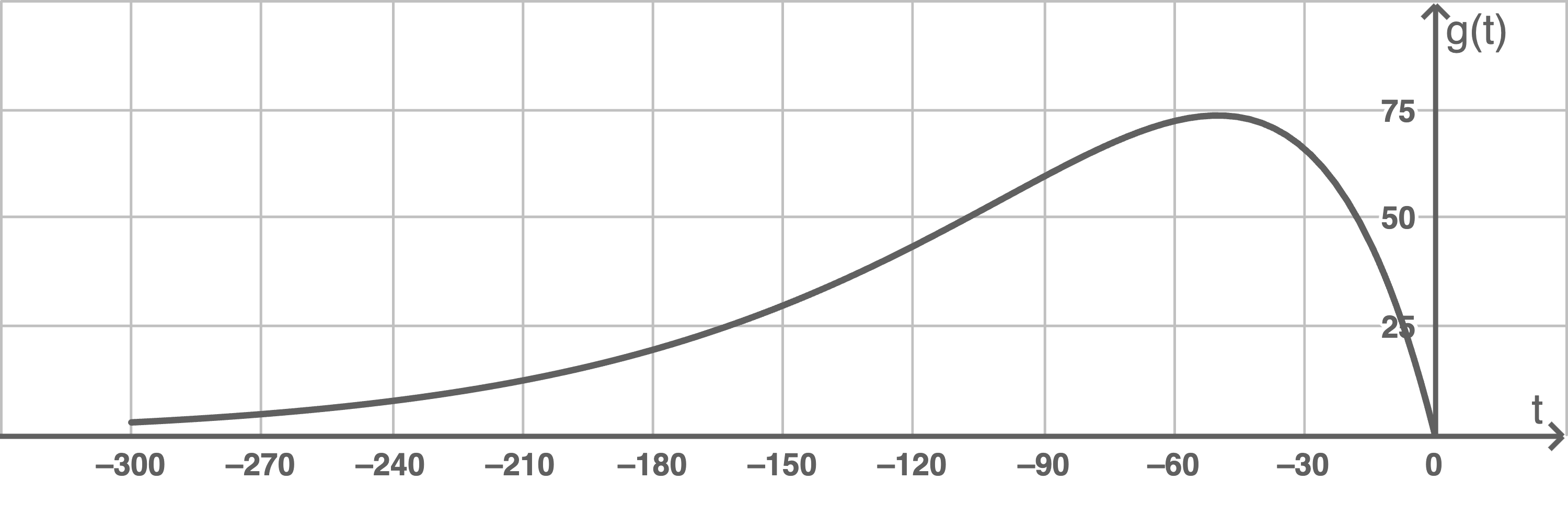
Abbildung 3: Änderungsrate der Personenanzahl auf dem Strandabschnitt vor dem Start

2.1

Begründe anhand des Funktionsterms, dass $g(t)$ für $t \leq 0$ keine negativen Werte annimmt, und erläutere, was dies im Sachzusammenhang bedeutet.

(3 BE)

2.2

Berechne die Uhrzeit (in Stunden und Minuten), zu der die Änderungsrate der Personenanzahl maximal ist.

Hinweis: Die Untersuchung der notwendigen Bedingung ist ausreichend.

(5 BE)

2.3

Zeige rechnerisch, dass die Funktion $G_1(t) = (-200t+10000)\cdot \mathrm e^{0,02\cdot t}$ die Bedingung $\(G$ erfüllt.

Begründe, dass die Funktion $G_1$ nicht die Personenanzahl auf dem Strandabschnitt darstellt, und gib die Gleichung derjenigen Funktion $G_2$ an, die die Personenanzahl auf dem Strandabschnitt für $t \lt 0$ beschreibt.

(5 BE)

2.4

Deute die Ergebnisse der Rechnungen $(1)$ und $(2)$ im Sachzusammenhang.

$(1)\quad \displaystyle\int_{-300}^{0}g(t)\;\mathrm dt\approx 9826$

$(2)\quad 10700 - \displaystyle\int_{-300}^{0}g(t)\;\mathrm dt \approx 874$

(3 BE)

2.5

Begründe mit Hilfe der Abbildung 3, dass sich die Personenanzahl auf dem Strandabschnitt im betrachteten Zeitraum innerhalb einer Stunde niemals um mehr als 4500 Personen erhöhen kann.

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Für die Geschwindigkeit der Rakete am Ende der Beschleunigungsphase, also nach 8 Minuten, gilt:

$\begin{array}[t]{rll} f(8)&=& -2 \cdot 8 ^3 + 24 \cdot 8^2& \\[5pt] &=& 512 \; \left[ \dfrac{\text{km}}{\text{min}} \right] \end{array}$

Umrechnung in Kilometer pro Stunde:

$512 \; \dfrac{\text{km}}{\text{min}} \cdot 60 \; \dfrac{\text{min}}{\text{h}}= 30720 \; \dfrac{\text{km}}{\text{h}}$

Die Rakete erreicht am Ende der Beschleunigungsphase somit eine Geschwindigkeit von 30720 Kilometer pro Stunde.

1.2

Wendestelle berechnen

Ableitungen bestimmen:

$\(\begin{array}[t]{rll} f$

Notwendige Bedingung für Wendestellen anwenden:

$\(\begin{array}[t]{rll} f$

Bedeutung erläutern

Die Wendestelle gibt den Zeitpunkt an, an dem die Beschleunigung am größten ist. Nach 4 Minuten erreicht die Rakete somit ihren maximalen Anstieg in der Geschwindigkeit.

1.3

Ableitungsfunktion begründen

Aus der Aufgabe 1.2 folgt, dass die Steigung an der Stelle $t=4$ am größten ist. Der Graph der Ableitungsfunktion von $f$ muss an dieser Stelle folglich ein Maximum besitzen.

Somit gehört der Graph B zur Ableitungsfunktion.

Bedeutung beschreiben

Die Stammfunktion von $f$ beschreibt den Flächeninhalt zwischen dem Graphen von $f$ und der $t$ -Achse und somit die Strecke, die in Abhängigkeit von der Zeit zurückgelegt wird.

Da die Rakete kontinuierlich steigt, wird die Distanz zum Space Center im Laufe der Zeit immer größer.

1.4

Wert berechnen

Stammfunktion aufstellen:

$\begin{array}[t]{rll} F(t)&=& \dfrac{1}{4} \cdot (-2) \cdot t^4 + \dfrac{1}{3} \cdot 24 \cdot t^3 & \\[5pt] &=& -\dfrac{1}{2} \cdot t^4 + 8\cdot t^3 \end{array}$

Es gilt also:

$\dfrac{1}{5} \cdot \displaystyle\int_{2}^{7}f(t)\;\mathrm dt= 297,5 \;[\text{km}]$

Rechenweg anzeigen

Ergebnis deuten

Von der zweiten bis zur siebten Minute der Beschleunigungsphase legt die Rakete eine Strecke von 297,5 Kilometer zurück.

2.1

Die Funktion $g$ nimmt keine negativen Funktionswerte an, da für die $\mathrm e$ -Funktion $\mathrm e^x\gt0$ gilt und der Faktor $-4t$ für $t \leq 0$ stets positiv ist.

Im Sachzusammenhang bedeutet dies, dass die Änderungsrate der Personenanzahl bis zum Start der Rakete nicht negativ wird und somit bis zum Raketenstart stets mehr Personen zum Strandabschnitt kommen, als wieder gehen.

2.2

Ableitung bestimmen:

$\(\begin{array}[t]{rll} g$

Notwendige Bedingung für Extremstellen anwenden:

$\(\begin{array}[t]{rll} g$

Die Änderungsrate der Personananzahl ist somit 50 Minuten vor dem Startzeitpunkt der Rakete , also um 18:10 Uhr, maximal.

2.3

Gleichung nachweisen

Mit der Produkt- und Kettenregel gilt:

$\( G_1$

Rechenweg anzeigen

Begründung

Die Funktion $G_1$ stellt die Personenanzahl auf dem Strandabschnitt erst ab dem Zeitpunkt 5 Stunden vor dem Raketenstart dar und berücksichtigt somit nicht diejenigen Personen, die schon zuvor dort waren.

Es muss also eine Konstante $P$ hinzugefügt werden, welche die Personenanzahl auf dem Strandabschnitt zu Beginn des Zeitintervalls, also zum Zeitpunkt 5 Stunden vor Start der Rakete, beschreibt:

$G_2(t) = P + G_1(t)$

2.4

Im ersten Schritt wird durch das Integral die Anzahl der Personen berechnet, die innerhalb der 5 Stunden vor Raketenstart auf den Strandabschnitt gekommen sind. Dies sind 9826 Personen.

Im zweiten Schritt wird die Anzahl der Personen, die innerhalb der 5 Stunden vor Start hinzugekommen sind, von der Gesamtanzahl der Personen auf dem Strandabschnitt beim Start der Rakete subtrahiert. Daher waren 5 Stunden vor Beginn des Starts bereits 874 Personen am Strand.

2.5

Aus der Abbildung kann die maximale Änderungsrate der Personenanzahl von etwa 75 Personen pro Minute abgelesen werden.

Innerhalb einer Stunde kann sich die Personenanzahl auf dem Strandabschnitt also nie um mehr als $75 \cdot 60=4500$ erhöhen.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?