Pflichtteil

Gegeben ist die Funktion $f$ mit $f(x)=\left(\frac{1}{2} x^2-\frac{1}{2} x-\frac{7}{4}\right) \cdot \mathrm{e}^{2 x+1},$ $x \in \mathbb{R}.$

(1)

Weise nach: $\(f$

(2)

Untersuche die Funktion $f$ auf lokale Extremstellen.

(2 + 3 Punkte)

Gegeben ist die Schar der in $\mathbb{R}$ definierten Funktionen $f_a$ mit $f_a(x)=a x^3+a x^2$ und $a \in \mathbb{R}, a \gt 0.$

(1)

Gib den Wert von $a$ an, so dass der Punkt $(1 \mid 6)$ auf dem Graphen von $f_a$ liegt.

(2)

Berechne in Abhängigkeit von $a$ den Inhalt der Fläche, die der Graph von $f_a$ mit der $x$ -Achse einschließt.

(1 + 4 Punkte)

Gegeben ist die Ebene $E: \overrightarrow{x}=\pmatrix{1\\-2\\3}+r \cdot\pmatrix{0\\2\\-4}$ $+s \cdot\pmatrix{1\\1\\1}, \;r, s \in \mathbb{R}.$

(1)

Ermittle eine Gleichung von $E$ in Koordinatenform.

[Mögliche Lösung: $E:-3 \cdot x_1+2 \cdot x_2+x_3=-4.$ ]

(2)

Berechne die Koordinaten des gemeinsamen Punktes der Ebene $E$ und der Gerade

$g: \overrightarrow{x}=\pmatrix{-1\\-2\\-3}+t \cdot\pmatrix{-3\\2\\1},t \in \mathbb{R}$

(3 + 2 Punkte)

Ein Glücksrad ist in 20 gleich große Sektoren unterteilt, die jeweils entweder blau oder gelb eingefärbt sind. Das Glücksrad wird 100-mal gedreht. Die binomialverteilte Zufallsgröße $X$ beschreibt, wie oft dabei die Farbe „Blau“, die binomialverteilte Zufallsgröße $Y,$ wie oft dabei die Farbe „Gelb“ erzielt wird.

(1)

Begründe, dass $X$ und $Y$ die gleiche Standardabweichung haben.

(2)

Der Erwartungswert von $X$ ist ganzzahlig. Die Abbildung zeigt Werte der Wahrscheinlichkeitsverteilung von $X.$

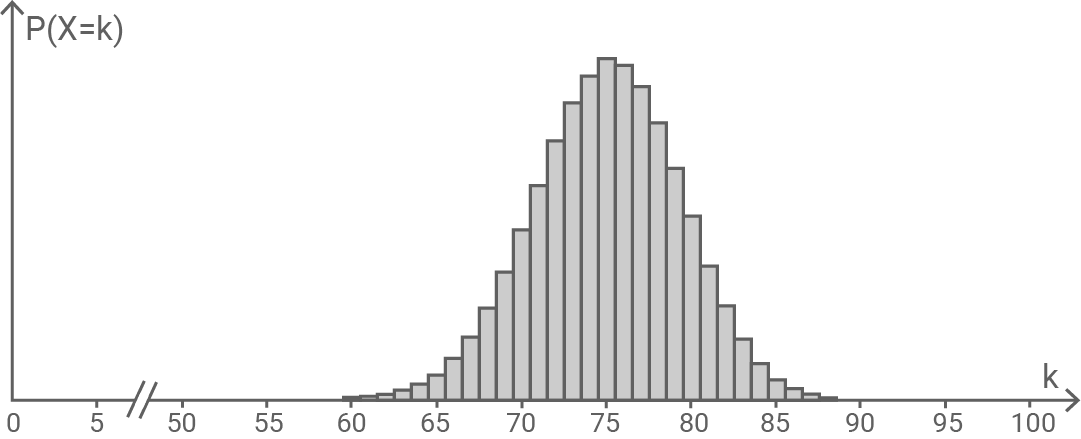Erwartungswert Gluecksrad Baden Wuerttemberg Mathe Abi 2024

Bestimme die Anzahl der blauen Sektoren des Glücksrads.

(2 + 3 Punkte)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

(1)

Mit der Produktregel folgt:

Rechenweg anzeigen

$\( f$

(2)

Mit der Produktregel folgt für $\(f$

Rechenweg anzeigen

$\( f$

1. Schritt: Notwendige Bedindung für Extremstellen anwenden

Da die $\mathrm e$ -Funktion stets ungleich null ist, folgt nach dem Satz des Nullprodukts:

$\(\begin{array}[t]{rll} f$

2. Schritt: Hinreichende Bedindung für Extremstellen überprüfen

$\(\begin{array}[t]{rll} f$

Somit besitzt die Funktion $f$ einen Tief- und einen Hochpunkt, und damit zwei lokale Extremstellen.

(1)

$\begin{array}[t]{rll} f_a(1)&=&6 \\[5pt] a\cdot1^3+a\cdot1^2&=&6 \\[5pt] 2a&=&6 &\quad \scriptsize \mid\;:2\\[5pt] a&=&3 \end{array}$

(2)

Nullstellen bestimmen

$\begin{array}[t]{rll} f_a(x)&=&0 \\[5pt] ax^3+ax^2&=&0 \\[5pt] ax^2\cdot(x+1)&=&0 \end{array}$

Da $ax^2=0$ wegen $a\in\mathbb{R}^+$ nur für $x=0$ gilt, folgt mit dem Satz des Nullprodukts $x_1=0$ und weiter:

$\begin{array}[t]{rll} x_2+1&=&0 &\quad \scriptsize \mid\;-1\\[5pt] x_2&=&-1 \end{array}$

Flächeninhalt berechnen

Rechenweg anzeigen

$A_a = \dfrac{1}{12}a$

(1)

Für einen Normalenvektor der Ebene $E$ folgt:

$\begin{array}[t]{rll} \overrightarrow{n}&=&\pmatrix{0\\2\\-4}\times\pmatrix{1\\1\\1} \\[5pt] &=&\pmatrix{2\cdot1-(-4)\cdot1\\(-4)\cdot1-0\\0-2\cdot 1} \\[5pt] &=&\pmatrix{6\\-4\\-2} \end{array}$

Mit dem Normalenvektor $-\frac{1}{2}\cdot\overrightarrow{n}$ folgt somit:

$E:-3\cdot x_1+2\cdot x_2+x_3=d$

Einsetzen der Koordinaten des Stützvektors der Ebene in diese Gleichung liefert:

$\begin{array}[t]{rll} -3\cdot1+2\cdot(-2)+3&=&d \\[5pt] -4&=&d \end{array}$

Eine mögliche Gleichung von $E$ in Koordinatenform ist somit gegeben durch $E:-3\cdot x_1+2\cdot x_2+x_3=-4.$

(2)

Einsetzen der Koordinaten eines allgemeinen Punktes der Gerade $g$ in die Gleichung von $E$ in Koordinatenform liefert:

Rechenweg anzeigen

$t = 0$

Einsetzen in die Geradengleichung liefert somit für den Ortsvektor des gemeinsamen Punktes $P:$

$\begin{array}[t]{rll} \overrightarrow{OP}&=&\pmatrix{-1\\-2\\-3}+0\cdot\pmatrix{-3\\2\\1} \\[5pt] &=&\pmatrix{-1\\-2\\-3} \end{array}$

Die Koordinaten des gemeinsamen Punktes der Ebene $E$ und der Gerade $g$ ergeben sich somit als $P(-1\mid -2\mid-3).$

(1)

Für die Standardabweichung gilt:

$\sigma=\sqrt{n\cdot p\cdot (1-p)}$

Der Parameter $n$ ist bei beiden Verteilung gleich und entspricht den 100 Drehungen.

Da außerdem jeweils die Wahrscheinlichkeit $p$ und die Gegenwahrscheinlichkeit $(1-p)$ multipliziert werden, wird bei beiden Standardabweichungen die Wahrscheinlichkeit für „Blau“ und für „Gelb“ multipliziert.

Damit haben $X$ und $Y$ folglich die gleiche Standardabweichung.

(2)

Aus der Wahrscheinlichkeitsverteilung von $X$ kann der Erwartungswert $\mu=75$ abgelesen werden.

Es gilt:

$\begin{array}[t]{rll} \mu&=& n\cdot p& \\[5pt] 75&=& 100\cdot \dfrac{x}{20}&\quad \scriptsize \mid\; :100 \\[5pt] 0,75&=& \dfrac{x}{20}&\quad \scriptsize \mid\; \cdot 20 \\[5pt] 15&=& x \end{array}$

Das Glücksrad besitzt somit 15 blaue Sektoren.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?