Aufgabe 3
Aufgabenstellung
In einem kartesischen Koordinatensystem sind die Punkte  ,
,  ,
,  ,
,  und
und  Eckpunkte der Pyramide
Eckpunkte der Pyramide  deren Grundfläche das Viereck
deren Grundfläche das Viereck  ist (siehe Abbildung).
ist (siehe Abbildung).
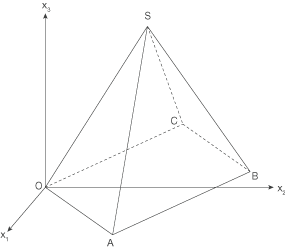 Abbildung
Im Folgenden darf verwendet werden, dass die Seitendreiecke der Pyramide zueinander kongruent sind.
Abbildung
Im Folgenden darf verwendet werden, dass die Seitendreiecke der Pyramide zueinander kongruent sind.
 Diese Ebene gehört zu der durch
Diese Ebene gehört zu der durch  , gegebenen Ebenenschar. [Zur Kontrolle:
, gegebenen Ebenenschar. [Zur Kontrolle:  .]
.]
 Abbildung
Abbildung
a) (1) Zeige, dass das Viereck  ein Quadrat ist.
ein Quadrat ist.
(5P)
(2) Berechne die Oberfläche der Pyramide  .
.
(5P)
b) (1) Leite eine Parameter- und eine Koordinatengleichung der Ebene  her, die durch die Punkte
her, die durch die Punkte  ,
,  und
und  festgelegt ist.
festgelegt ist.
(5P)
(2) Zeige, dass die Punkte  und
und  in jeder Ebene
in jeder Ebene  liegen.
liegen.
(3P)
(3) Nenne ohne Nachweis die verschiedenen Arten von Schnittgebilden, die beim Schnitt einer der Ebenen  mit der Pyramide
mit der Pyramide  entstehen können.
entstehen können.
(4P)
(4) Für genau einen Wert von  ist das Schnittgebilde von Ebene und Pyramide ein Dreieck.
Bestimme den entsprechenden Wert von
ist das Schnittgebilde von Ebene und Pyramide ein Dreieck.
Bestimme den entsprechenden Wert von  .
.
(3P)
(5) Die Ebene  zerlegt die Pyramide
zerlegt die Pyramide  in zwei Teilkörper. Sie können ohne Nachweis verwenden, dass das Schnittgebilde den Flächeninhalt
in zwei Teilkörper. Sie können ohne Nachweis verwenden, dass das Schnittgebilde den Flächeninhalt ![\(\dfrac{400}{9}\cdot\sqrt{2}\,[\text{FE}]\)](https://mathjax.schullv.de/dae0d22e008004a4f4f7f7c9f281488efd6f42e288fc655347656173c1d3dd32?color=5a5a5a) besitzt.
Bestimme ein Verhältnis der Rauminhalte der beiden Teilkörper.
besitzt.
Bestimme ein Verhältnis der Rauminhalte der beiden Teilkörper.
(8P)
c) Auf der Geraden  gibt es genau einen Punkt
gibt es genau einen Punkt  , so dass die Strecken
, so dass die Strecken  und
und  senkrecht zu
senkrecht zu  sind.
sind.
(1) Bestimme die Koordinaten von  .
[Zur Kontrolle:
.
[Zur Kontrolle:  .]
.]
(6P)
(2) Begründe, dass der Streckenzug  ein kürzester Weg von
ein kürzester Weg von  nach
nach  über den Mantel der Pyramide (Mantel: Oberfläche ohne Grundfläche) ist, und berechne die Länge des Streckenzuges.
über den Mantel der Pyramide (Mantel: Oberfläche ohne Grundfläche) ist, und berechne die Länge des Streckenzuges.
(5P)
(3) Es gibt einen weiteren Streckenzug  , der ein kürzester Weg von
, der ein kürzester Weg von  nach
nach  über den Mantel der Pyramide ist.
Begründe diese Aussage und bestimme die Koordinaten von
über den Mantel der Pyramide ist.
Begründe diese Aussage und bestimme die Koordinaten von  .
.
(6P)
a)(1)
 Zeigen, dass
Zeigen, dass  ein Quadrat ist
Hier ist es deine Aufgabe zu zeigen, dass das Viereck
ein Quadrat ist
Hier ist es deine Aufgabe zu zeigen, dass das Viereck  ein Quadrat ist. Die Punkte
ein Quadrat ist. Die Punkte  ,
,  ,
,  und
und  liegen dabei in der
liegen dabei in der  -
- -Ebene. Also musst du Folgendes tun:
-Ebene. Also musst du Folgendes tun:
 ein Quadrat ist.
1. Schritt: Verbindungsvektoren berechnen
Die Seiten des Vierecks sind hier die Strecken
ein Quadrat ist.
1. Schritt: Verbindungsvektoren berechnen
Die Seiten des Vierecks sind hier die Strecken  ,
,  ,
,  und
und  . Berechne die dazugehörigen Verbindungsvektoren:
. Berechne die dazugehörigen Verbindungsvektoren:



 Damit sind insbesondere die gegenüberliegenden Seiten
Damit sind insbesondere die gegenüberliegenden Seiten  und
und  , sowie
, sowie  und
und  gleich lang.
2. Schritt: Zeigen, dass alle Seiten gleich lang sind
Im 1. Schritt hast du bereits gezeigt, dass die gegenüberliegenden Seiten gleich lang sind. Nun musst du nur noch zeigen, dass zwei anliegende Seiten gleich lang sind. Ist dies der Fall, so sind alle Seiten gleich lang. Zeige also, dass
gleich lang.
2. Schritt: Zeigen, dass alle Seiten gleich lang sind
Im 1. Schritt hast du bereits gezeigt, dass die gegenüberliegenden Seiten gleich lang sind. Nun musst du nur noch zeigen, dass zwei anliegende Seiten gleich lang sind. Ist dies der Fall, so sind alle Seiten gleich lang. Zeige also, dass  . Den Vektorbetrag kannst du mit dem norm-Befehl deines CAS berechnen. Den Befehl für Vektoren findest du unter
menu
. Den Vektorbetrag kannst du mit dem norm-Befehl deines CAS berechnen. Den Befehl für Vektoren findest du unter
menu  7: Matrix und Vektor
7: Matrix und Vektor  1: Erstellen
1: Erstellen  1: Matrix
1: Matrix


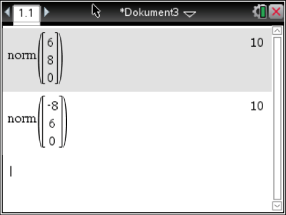 Somit sind alle Seiten gleich lang.
3. Schritt: Zeigen, dass jeder Innenwinkel ein rechter Winkel ist
Hier reicht es zu zeigen, dass ein Innenwinkel 90° ist. Da alle Seiten des Vierecks gleich lang sind, kannst du daraus folgern, dass alle Innenwinkel rechte Winkel sind. Dies kannst du mit dem Skalarpodukt zeigen. Ist das Skalarprodukt zweier Vektoren gleich Null, so stehen die Vektoren senkrecht aufeinander. Berechne also
Somit sind alle Seiten gleich lang.
3. Schritt: Zeigen, dass jeder Innenwinkel ein rechter Winkel ist
Hier reicht es zu zeigen, dass ein Innenwinkel 90° ist. Da alle Seiten des Vierecks gleich lang sind, kannst du daraus folgern, dass alle Innenwinkel rechte Winkel sind. Dies kannst du mit dem Skalarpodukt zeigen. Ist das Skalarprodukt zweier Vektoren gleich Null, so stehen die Vektoren senkrecht aufeinander. Berechne also  . Hierzu kannst du den dotP-Befehl deines CAS verwenden.
. Hierzu kannst du den dotP-Befehl deines CAS verwenden.

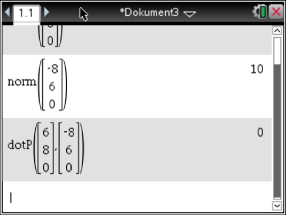 Damit hast du gezeigt, dass alle Innenwinkel des Vierecks rechte Winkel sind. Für das Viereck
Damit hast du gezeigt, dass alle Innenwinkel des Vierecks rechte Winkel sind. Für das Viereck  hast du nun alle 3 Bedingungen gezeigt, also ist
hast du nun alle 3 Bedingungen gezeigt, also ist  ein Quadrat.
a)(2)
ein Quadrat.
a)(2)
 Oberfläche der Pyramide berechnen
Der Flächeninhalt der Oberfläche
Oberfläche der Pyramide berechnen
Der Flächeninhalt der Oberfläche  ist durch eine Formel gegeben:
ist durch eine Formel gegeben:
 Hier ist
Hier ist  der Flächeninhalt der Grundfläche der Pyramide,
der Flächeninhalt der Grundfläche der Pyramide,  ist der Flächeninhalt der Mantelfläche der Pyramide.
Die Grundfläche der Pyramide hat gerade die Form eines Quadrats. Die Länge der Seiten der Grundfläche hast du bereits in (1) berechnet. Also kannst du
ist der Flächeninhalt der Mantelfläche der Pyramide.
Die Grundfläche der Pyramide hat gerade die Form eines Quadrats. Die Länge der Seiten der Grundfläche hast du bereits in (1) berechnet. Also kannst du  folgendermaßen berechnen:
folgendermaßen berechnen:
 Die Mantelfläche der Pyramide setzt sich aus den vier Seitendreiecken zusammen und entsprechendes gilt daher auch für den Flächeninhalt der Mantelfläche. Du kannst verwenden, dass die Seitendreiecke kongruent sind, also sind ihre Flächen gleich groß. Für den Flächeninhalt
Die Mantelfläche der Pyramide setzt sich aus den vier Seitendreiecken zusammen und entsprechendes gilt daher auch für den Flächeninhalt der Mantelfläche. Du kannst verwenden, dass die Seitendreiecke kongruent sind, also sind ihre Flächen gleich groß. Für den Flächeninhalt  eines Seitendreiecks ist der Flächeninhalt der Mantelfläche durch folgende Formel gegeben:
eines Seitendreiecks ist der Flächeninhalt der Mantelfläche durch folgende Formel gegeben:
 Berechne also zuerst den Flächeninhalt eines Seitendreiecks. Wähle das Seitendreieck
Berechne also zuerst den Flächeninhalt eines Seitendreiecks. Wähle das Seitendreieck  . Du benötigst nun die Höhe und die Länge der Grundseite des Dreiecks
. Du benötigst nun die Höhe und die Länge der Grundseite des Dreiecks  . Wähle als Grundseite des Dreiecks die Seite
. Wähle als Grundseite des Dreiecks die Seite  . Mit der Höhe
. Mit der Höhe  des Dreiecks kannst du die Fläche des Dreiecks folgendermaßen berechnen:
des Dreiecks kannst du die Fläche des Dreiecks folgendermaßen berechnen:
 Du musst noch die Höhe
Du musst noch die Höhe  berechnen. Betrachte dazu die untenstehende Skizze:
berechnen. Betrachte dazu die untenstehende Skizze:
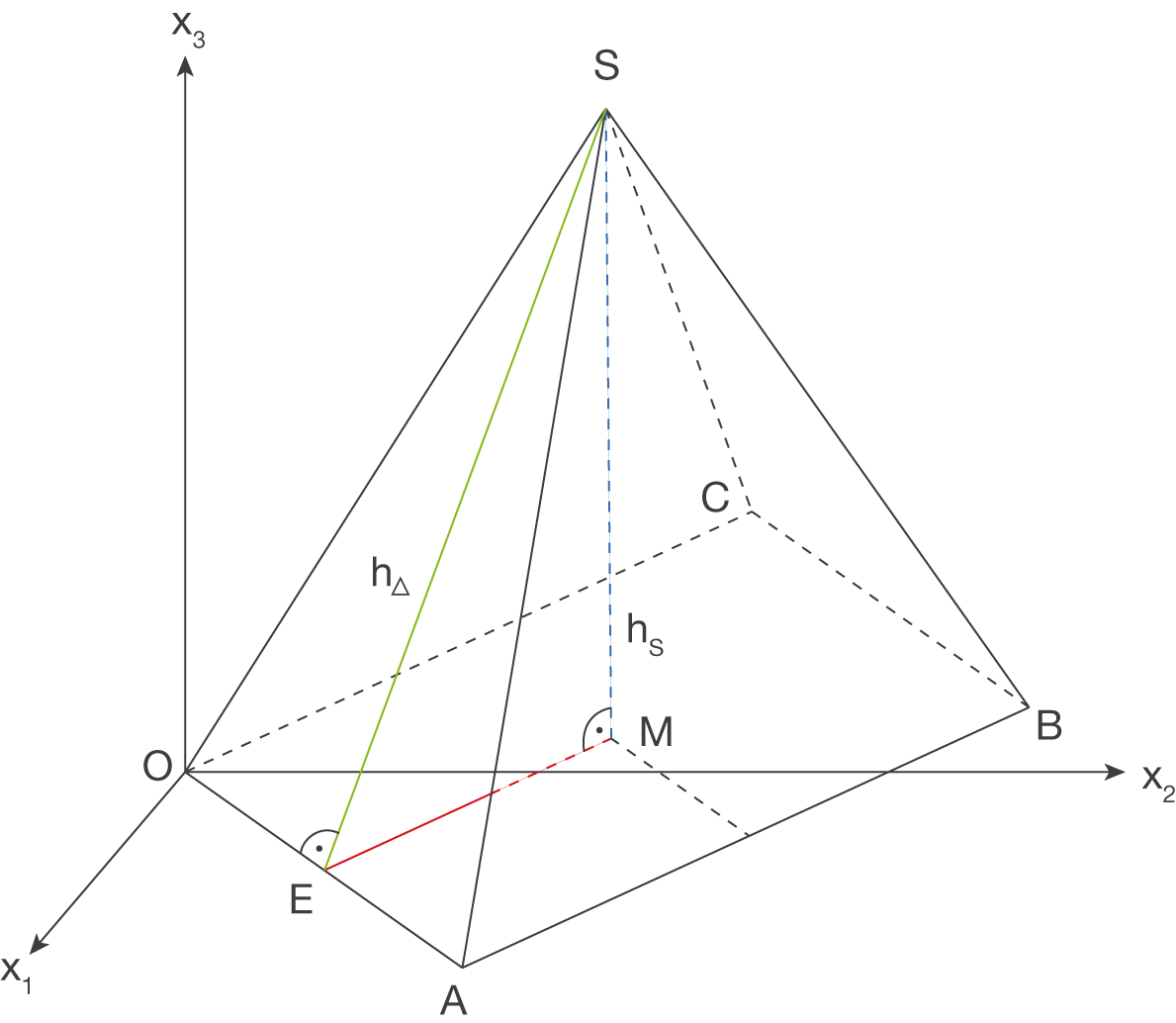 Das Dreieck mit den Eckpunkten
Das Dreieck mit den Eckpunkten  ist rechtwinklig und die Strecke zwischen
ist rechtwinklig und die Strecke zwischen  und
und  entspricht der Höhe
entspricht der Höhe  . Also kannst du die Höhe
. Also kannst du die Höhe  mit dem Satz des Pythagoras berechnen.
mit dem Satz des Pythagoras berechnen.
 ist gerade die Höhe der Pyramide. Da die Grundfläche der Pyramide in der
ist gerade die Höhe der Pyramide. Da die Grundfläche der Pyramide in der  -
- -Ebene liegt, ist die Höhe der Pyramide durch die
-Ebene liegt, ist die Höhe der Pyramide durch die  -Koordinate von
-Koordinate von  gegeben. Also ist
gegeben. Also ist  . Es fehlt nun noch die Länge der Strecke
. Es fehlt nun noch die Länge der Strecke  . Der Punkt
. Der Punkt  ist gerade der Mittelpunkt der Grundfläche. Diese ist quadratisch und somit ist die Länge der Strecke
ist gerade der Mittelpunkt der Grundfläche. Diese ist quadratisch und somit ist die Länge der Strecke  die Hälfte der Länge der Seite
die Hälfte der Länge der Seite  . Also gilt:
. Also gilt:
 Nun kannst du die Höhe
Nun kannst du die Höhe  mit dem Satz des Pythagoras ausrechnen:
mit dem Satz des Pythagoras ausrechnen:
 Also:
Also:  Damit kannst du nun die Oberfläche der Pyramide berechnen:
Damit kannst du nun die Oberfläche der Pyramide berechnen:
![\(\begin{array}[t]{rll}
A&=A_G+A_M& \quad \scriptsize \mid\; A_M=4 \cdot A_\triangle\\[5pt]
&=A_G+4\cdot A_M&\quad \scriptsize \mid\; A_\triangle=\dfrac{1}{2} \cdot h_\triangle \cdot \left|\overrightarrow{OA}\right| \\[5pt]
&=A_G + 4 \cdot \dfrac{1}{2} \cdot h_\triangle \cdot \left|\overrightarrow{OA}\right| \\[5pt]
&=A_G + 2 \cdot h_\triangle \cdot \left|\overrightarrow{OA}\right|
\end{array}\)](https://mathjax.schullv.de/ce842aacdf8df70e6047fabf2fd5b431255eac30a14e32a7815700942186c24b?color=5a5a5a) Hier kannst du die oben berechneten Werte einsetzen:
Hier kannst du die oben berechneten Werte einsetzen:
![\(\begin{array}[t]{rll}
A&=100 + 2 \cdot 11,18 \cdot 10 \\[5pt]
&=100 + 223,6 \\[5pt]
&=323,61
\end{array}\)](https://mathjax.schullv.de/a37dd00c96756a95055860a2027e7d1482f7df362630e404c910a04984ee29c8?color=5a5a5a) Die Oberfläche der Pyramide ist
Die Oberfläche der Pyramide ist  [FE].
[FE].
- Verbindungsvektoren, die die Seiten beschreiben, berechnen.
- Zeige, dass alle Seiten gleich lang sind. Die Länge der Seiten kannst du mit den Beträgen der entsprechenden Verbindungsvektoren berechnen.
- Zeige, dass jeder Innenwinkel ein rechter Winkel ist. Dies kannst du mit dem Skalarprodukt zeigen.



b)(1)
 Parameter- und Koordinatengleichung der Ebene
Parameter- und Koordinatengleichung der Ebene  herleiten
Da du drei Punkte gegeben hast, die in der Ebene
herleiten
Da du drei Punkte gegeben hast, die in der Ebene  liegen, ist es sinnvoll, zunächst die Parameterform der Ebene
liegen, ist es sinnvoll, zunächst die Parameterform der Ebene  zu berechnen. Lege dazu fest, welchen Ortsvektor du als Stützvektor und welche Verbindungsvektoren du als Spannvektoren betrachtest. Diese kannst du dann in die Parameterform einsetzen.
Anschließend kannst du die Parameterform in die gesuchte Koordinatenform umwandeln. Berechne dazu den Normalenvektor
zu berechnen. Lege dazu fest, welchen Ortsvektor du als Stützvektor und welche Verbindungsvektoren du als Spannvektoren betrachtest. Diese kannst du dann in die Parameterform einsetzen.
Anschließend kannst du die Parameterform in die gesuchte Koordinatenform umwandeln. Berechne dazu den Normalenvektor  aus dem Vektorprodukt der beiden Spannvektoren und den Parameter
aus dem Vektorprodukt der beiden Spannvektoren und den Parameter  mit Hilfe einer Punktprobe. Damit erhältst du eine Koordinatengleichung der Ebene
mit Hilfe einer Punktprobe. Damit erhältst du eine Koordinatengleichung der Ebene  durch Einsetzen in die allgemeine Koordinatenform.
1. Schritt: Ebenengleichung in Parameterform aufstellen
Wähle zunächst den Stützvektor und die Spannvektoren:
durch Einsetzen in die allgemeine Koordinatenform.
1. Schritt: Ebenengleichung in Parameterform aufstellen
Wähle zunächst den Stützvektor und die Spannvektoren:
 sei der Stützvektor,
sei der Stützvektor,  und
und  die Spannvektoren.
Du erhältst:
die Spannvektoren.
Du erhältst:


 .
Einsetzen in die Parameterform liefert:
.
Einsetzen in die Parameterform liefert:
 2. Schritt: Parameterform in Koordinatenform umwandeln
Für die Koordinatenform benötigst du zunächst den Normalenvektor
2. Schritt: Parameterform in Koordinatenform umwandeln
Für die Koordinatenform benötigst du zunächst den Normalenvektor  , den du mittels Vektorprodukt der beiden Spannvektoren bestimmen kannst. Anschließend kannst du den Parameter
, den du mittels Vektorprodukt der beiden Spannvektoren bestimmen kannst. Anschließend kannst du den Parameter  mit Hilfe einer Punktprobe bestimmen. Das Kreuzprodukt lässt sich mit dem crossP-Befehl deines CAS berechnen:
mit Hilfe einer Punktprobe bestimmen. Das Kreuzprodukt lässt sich mit dem crossP-Befehl deines CAS berechnen:

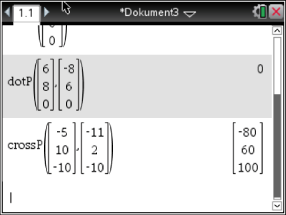 Bestimme den Parameter
Bestimme den Parameter  mit Hilfe einer Punktprobe:
Du weißt bereits, dass
mit Hilfe einer Punktprobe:
Du weißt bereits, dass  aufgrund der Konstruktion in der Ebene
aufgrund der Konstruktion in der Ebene  liegt. Setze also
liegt. Setze also  zusammen mit dem Normalenvektor in die Koordinatenform ein, um den Parameter
zusammen mit dem Normalenvektor in die Koordinatenform ein, um den Parameter  zu ermitteln:
zu ermitteln:
 Einsetzen in die allgemeine Koordinatenform liefert das Ergebnis:
Einsetzen in die allgemeine Koordinatenform liefert das Ergebnis:
![\(\begin{array}{rll}
E: &-80\cdot x_1 + 60\cdot x_2 + 100 \cdot x_3 =1.000 &\scriptsize \mid \ :4
\\[5pt]
E: &-20 \cdot x_1 + 15\cdot x_2 + 25 \cdot x_3 =250
\end{array}\)](https://mathjax.schullv.de/b4f93f06cf63f34cddb0c3ef02a96ba1f4d6c36e47b7ea49ef8a3625ac5866b9?color=5a5a5a) Je nachdem, welche Vektoren als Stütz- und Spannvektoren gewählt wurden, sind noch andere Lösungsansätze möglich.
b)(2)
Je nachdem, welche Vektoren als Stütz- und Spannvektoren gewählt wurden, sind noch andere Lösungsansätze möglich.
b)(2)
 Lage der Punkte
Lage der Punkte  und
und  in jeder Ebene
in jeder Ebene  nachweisen
Führe eine Punktprobe durch, um zu zeigen, dass die Punkte
nachweisen
Führe eine Punktprobe durch, um zu zeigen, dass die Punkte  und
und  in jeder Ebene
in jeder Ebene  liegen. Setze dazu die Koordinaten der Punkte in die allgemeine Koordinatengleichung
liegen. Setze dazu die Koordinaten der Punkte in die allgemeine Koordinatengleichung  ein und zeige, dass diese für alle
ein und zeige, dass diese für alle  erfüllt ist.
erfüllt ist.
 Lage von
Lage von  in jeder Ebene
in jeder Ebene  nachweisen
Einsetzen von
nachweisen
Einsetzen von  in
in  liefert:
liefert:
![\(\begin{array}[t]{rll}
-4\cdot a \cdot (-2) + 3\cdot a \cdot 14 + 25 \cdot 0 =&50\cdot a
\\[5pt]
8\cdot a + 42\cdot a =&50\cdot a
\\[5pt]
50\cdot a =&50\cdot a &\scriptsize \mid\; :50
\\[5pt]
a =& a
\end{array}\)](https://mathjax.schullv.de/cf76dec661fa15c8875c321e5984e1ad27b5d42feab6c04087b2d7c6b1efec18?color=5a5a5a) Diese Gleichung gilt für alle
Diese Gleichung gilt für alle  , also liegt der Punkt
, also liegt der Punkt  in jeder Ebene
in jeder Ebene  .
.
 Lage von
Lage von  in jeder Ebene
in jeder Ebene  nachweisen
Einsetzen von
nachweisen
Einsetzen von  in
in  liefert:
liefert:
![\(\begin{array}[t]{rll}
-4\cdot a \cdot (-8) + 3\cdot a \cdot 6 + 25 \cdot 0 =&50\cdot a
\\[5pt]
32\cdot a + 18\cdot a =&50\cdot a
\\[5pt]
50\cdot a =&50\cdot a &\scriptsize \mid\; :50
\\[5pt]
a =& a
\end{array}\)](https://mathjax.schullv.de/7365156071f53e31989ca8a82f8a66f00f0e203e31b99169bfcb983bb7ef0952?color=5a5a5a) Diese Gleichung gilt für alle
Diese Gleichung gilt für alle  , also liegt der Punkt
, also liegt der Punkt  in jeder Ebene
in jeder Ebene  .
b)(3)
.
b)(3)
 Verschiedene Arten der Schnittgebilde nennen
Im vorigen Aufgabenteil hast du bewiesen, dass die Punkte
Verschiedene Arten der Schnittgebilde nennen
Im vorigen Aufgabenteil hast du bewiesen, dass die Punkte  und
und  in jeder der Ebenen
in jeder der Ebenen  liegen. Damit enthält jede Ebene
liegen. Damit enthält jede Ebene  die Seitenkante
die Seitenkante  der Pyramide. Überlege dir nun, auf welche verschiedenen Arten eine solche Ebene
der Pyramide. Überlege dir nun, auf welche verschiedenen Arten eine solche Ebene  die Pyramide schneiden kann und welche Schnittgebilde daraus entstehen:
die Pyramide schneiden kann und welche Schnittgebilde daraus entstehen:
 Gesuchten Wert von
Gesuchten Wert von  bestimmen
Damit das Schnittgebilde von Ebene und Pyramide ein Dreieck ist, muss das Seitendreieck
bestimmen
Damit das Schnittgebilde von Ebene und Pyramide ein Dreieck ist, muss das Seitendreieck  in der Ebene liegen. Also ist die Ebene
in der Ebene liegen. Also ist die Ebene  gesucht, in der die Punkte
gesucht, in der die Punkte  ,
,  und
und  liegen.
Da
liegen.
Da  und
und  in jeder Ebene liegen, musst du die Ebene
in jeder Ebene liegen, musst du die Ebene  bestimmen, die auch
bestimmen, die auch  enthält. Dazu kannst du die Koordinaten von
enthält. Dazu kannst du die Koordinaten von  in die allgemeine Koordinatengleichung
in die allgemeine Koordinatengleichung  einsetzen und nach
einsetzen und nach  auflösen:
auflösen:
![\(\begin{array}[t]{rll}
-4\cdot a \cdot (-1) + 3\cdot a \cdot 7 + 25 \cdot 10 =&50\cdot a
\\[5pt]
4\cdot a + 21\cdot a + 250 =&50\cdot a & \scriptsize \mid\; - 25\cdot a
\\[5pt]
250 =&25\cdot a & \scriptsize \mid\; : 25
\\[5pt]
10 =&a
\end{array}\)](https://mathjax.schullv.de/e5b519665af247175e46730e2b736d8b9f64ead48e207ff5890826a5f4e8e162?color=5a5a5a) Also ist für
Also ist für  das Schnittgebilde von Ebene und Pyramide das Dreieck
das Schnittgebilde von Ebene und Pyramide das Dreieck  .
b)(5)
.
b)(5)
 Verhältnis der Rauminhalte der beiden Teilkörper bestimmen
Die Ebene
Verhältnis der Rauminhalte der beiden Teilkörper bestimmen
Die Ebene  zerlegt die Pyramide
zerlegt die Pyramide  in eine „kleine“ Pyramide mit Spitze
in eine „kleine“ Pyramide mit Spitze  (oberer Teilkörper) und einen „Restkörper“, was du in folgender Skizze gut erkennen kannst:
(oberer Teilkörper) und einen „Restkörper“, was du in folgender Skizze gut erkennen kannst:
 Um das Verhältnis der Rauminhalte der beiden Körper zu bestimmen, kannst du wie folgt vorgehen:
Um das Verhältnis der Rauminhalte der beiden Körper zu bestimmen, kannst du wie folgt vorgehen:
 Dabei ist
Dabei ist  die Grundfläche der Pyramide und
die Grundfläche der Pyramide und  die Höhe der Pyramide.
1. Schritt: Volumen der Pyramide
die Höhe der Pyramide.
1. Schritt: Volumen der Pyramide  berechnen
Die Grundfläche der Pyramide
berechnen
Die Grundfläche der Pyramide  und die Höhe
und die Höhe  hast du bereits in Aufgabe a) (2) berechnet.
hast du bereits in Aufgabe a) (2) berechnet.
 .
2. Schritt: Volumen der „kleinen“ Pyramide berechnen
Die Grundfläche der „kleinen“ Pyramide
.
2. Schritt: Volumen der „kleinen“ Pyramide berechnen
Die Grundfläche der „kleinen“ Pyramide  ist in der Aufgabenstellung gegeben. Berechne also die Höhe
ist in der Aufgabenstellung gegeben. Berechne also die Höhe  .
Bestimme zunächst die Hesse‘sche Normalenform von der Ebene
.
Bestimme zunächst die Hesse‘sche Normalenform von der Ebene  . Lese dazu den Normalenvektor
. Lese dazu den Normalenvektor
 :
aus der Koordinatengleichung von
:
aus der Koordinatengleichung von  ab und bestimme dessen Länge:
ab und bestimme dessen Länge:
 Damit erhältst du die Hesse‘sche Normalenform von
Damit erhältst du die Hesse‘sche Normalenform von  :
:
 .
Einsetzen von
.
Einsetzen von  in die linke Seite der Hesse‘schen Normalenform von
in die linke Seite der Hesse‘schen Normalenform von  liefert dir den Abstand von
liefert dir den Abstand von  zur Ebene
zur Ebene  , was gerade der gesuchten Höhe entspricht:
, was gerade der gesuchten Höhe entspricht:
 Nun kannst du
Nun kannst du  und
und  in die Formel zum Berechnen des Volumens einer Pyramide einsetzen und erhältst für das Volumen
in die Formel zum Berechnen des Volumens einer Pyramide einsetzen und erhältst für das Volumen  der „kleinen“ Pyramide:
der „kleinen“ Pyramide:
 .
3. Schritt: Volumen des „Restkörpers“ berechnen
Das Volumen
.
3. Schritt: Volumen des „Restkörpers“ berechnen
Das Volumen  des „Restkörpers“ ist die Differenz aus den Volumina der gesamten und der „kleinen“ Pyramide, also:
des „Restkörpers“ ist die Differenz aus den Volumina der gesamten und der „kleinen“ Pyramide, also:
 .
4. Schritt: Verhältnis ermitteln
Setze die beiden errechneten Volumina in Verhältnis zueinander:
.
4. Schritt: Verhältnis ermitteln
Setze die beiden errechneten Volumina in Verhältnis zueinander:
 .
Damit beträgt das Verhältnis von der „kleinen“ Pyramide zum „Restkörper“
.
Damit beträgt das Verhältnis von der „kleinen“ Pyramide zum „Restkörper“  .
.

- Strecke: Die Ebene
schneidet die Pyramide nur in der Seitenkante
.
- Dreieck: Die Ebene
schneidet die Pyramide im Seitendreieck
.
- Quadrat: Die Ebene
schneidet die Pyramide im Viereck
.
- Trapez: Die Ebene
schneidet die Pyramide in der Trapezfläche, die durch
,
und jeweils einen Punkt auf der Seitenkanten
und
definiert ist.

- Bestimme zunächst das Volumen der Pyramide
. Nutze dazu die bereits in Aufgabe a)(2) berechneten Werte für Grundfläche und Höhe der Pyramide.
- Berechne anschließend das Volumen der „kleinen“ Pyramide. Die Höhe der kleinen Pyramide ist der Abstand der Spitze
von der Ebene
, den du über die Hesse‘sche Normalenform berechnen kannst. Die Grundfläche ist in der Aufgabenstellung gegeben.
- Das Volumen des „Restkörpers“ ergibt sich aus der Differenz der „kleinen“ Pyramide und der Pyramide
.
- Damit kannst du dann das Verhältnis der Rauminhalte der beiden Teilkörper ermitteln.
c)(1)
 Koordinaten von
Koordinaten von  bestimmen
Der gesuchte Punkt
bestimmen
Der gesuchte Punkt  soll auf der Geraden
soll auf der Geraden  liegen und erfüllen, dass
liegen und erfüllen, dass  und
und  senkrecht zu
senkrecht zu  sind. Ermittle also eine Geradengleichung von
sind. Ermittle also eine Geradengleichung von  , um die Form der Koordinaten des Punktes
, um die Form der Koordinaten des Punktes  in Abhängigkeit des Parameters der Geradengleichung zu erhalten. Anschließend kannst du den genauen Parameter für
in Abhängigkeit des Parameters der Geradengleichung zu erhalten. Anschließend kannst du den genauen Parameter für  bestimmen, indem du das Skalarprodukt von
bestimmen, indem du das Skalarprodukt von  oder
oder  und dem Richtungsvektor von
und dem Richtungsvektor von  berechnest, das gleich Null sein muss.
Da die Punkte
berechnest, das gleich Null sein muss.
Da die Punkte  und
und  auf der Geraden
auf der Geraden  liegen, kannst du
liegen, kannst du  als Stützvektor der Geraden und den Verbindungsvektor
als Stützvektor der Geraden und den Verbindungsvektor  als Richtungsvektor auffassen. Somit ergibt sich die Geradengleichung
als Richtungsvektor auffassen. Somit ergibt sich die Geradengleichung  :
:
 Also hat ein Punkt
Also hat ein Punkt  auf der Geraden
auf der Geraden  folgende Gestalt:
folgende Gestalt:
 .
Damit
.
Damit  senkrecht zur Geraden
senkrecht zur Geraden  ist, muss das Skalarprodukt aus
ist, muss das Skalarprodukt aus  und dem Richtungsvektor von
und dem Richtungsvektor von  gerade Null ergeben, die daraus resultierende Gleichung kannst du mit dem solve-Befehl deines CAS nach
gerade Null ergeben, die daraus resultierende Gleichung kannst du mit dem solve-Befehl deines CAS nach  lösen:
lösen:
![\(\begin{array}[t]{rll}
\begin{pmatrix} 6-7 \cdot r\\8 - r\\10 \cdot r\end{pmatrix} \circ \begin{pmatrix}-7\\-1\\10\end{pmatrix} \stackrel{!}{=}&0
\\[5pt]
r =& \dfrac{1}{3}
\end{array}\)](https://mathjax.schullv.de/2dbc0e91a7dd2293550d658193b6846e076566b7bcb53ef8ffb8109e088c76c4?color=5a5a5a)
 Einsetzen von
Einsetzen von  in die Koordinaten von
in die Koordinaten von  ergibt:
ergibt:
 Da man nur eine mögliche Lösung erhält, sind dies die gesuchten Koordinaten von
Da man nur eine mögliche Lösung erhält, sind dies die gesuchten Koordinaten von  . Also lauten die Koordinaten
. Also lauten die Koordinaten  .
c)(2)
.
c)(2)

 als einen kürzesten Weg begründen
Ein kürzester Weg von einem Punkt zu einer Geraden ist das Lot vom Punkt auf die Gerade. Nutze diese Eigenschaft, um die Behauptung zu begründen.
Zunächst gilt, dass der Punkt
als einen kürzesten Weg begründen
Ein kürzester Weg von einem Punkt zu einer Geraden ist das Lot vom Punkt auf die Gerade. Nutze diese Eigenschaft, um die Behauptung zu begründen.
Zunächst gilt, dass der Punkt  auf der Seitenkante
auf der Seitenkante  liegt:
liegt:

 ist Fußpunkt des Lotes von
ist Fußpunkt des Lotes von  auf
auf  sowie des Lotes von
sowie des Lotes von  auf
auf  , was du im vorigen Aufgabenteil bewiesen hast (
, was du im vorigen Aufgabenteil bewiesen hast ( und
und  sind senkrecht zu
sind senkrecht zu  ). Damit ist
). Damit ist  der kürzeste Weg von
der kürzeste Weg von  zur Geraden
zur Geraden  und
und  der kürzeste Weg von
der kürzeste Weg von  zur Geraden
zur Geraden  . Deswegen ist der Streckenzug
. Deswegen ist der Streckenzug  der kürzeste Weg von
der kürzeste Weg von  nach
nach  über die Dreiecksflächen
über die Dreiecksflächen  und
und  .
Da die Ebene
.
Da die Ebene  , die durch die Punkte
, die durch die Punkte  ,
,  und
und  bestimmt ist, eine Symmetrieebene der Pyramide ist (
bestimmt ist, eine Symmetrieebene der Pyramide ist ( teilt die Pyramide in zwei symmetrische Teilkörper), gibt es keinen kürzeren Weg über die Dreiecksflächen
teilt die Pyramide in zwei symmetrische Teilkörper), gibt es keinen kürzeren Weg über die Dreiecksflächen  und
und  .
.
 Länge des Streckenzugs berechnen
Berechne die Länge des Streckenzugs
Länge des Streckenzugs berechnen
Berechne die Länge des Streckenzugs  als Summe der Länge der Vektoren
als Summe der Länge der Vektoren  und
und  .
.
![\(\begin{array}[t]{rll}
\left|\overline{OPB}\right|=& \left|\overrightarrow{OP}\right| + \left|\overrightarrow{BP}\right|
\\[5pt]
=&\left|\begin{pmatrix} \frac{11}{3}\\\frac{23}{3}\\\frac{10}{3}\end{pmatrix}\right| + \left|\begin{pmatrix} -\frac{17}{3}\\\frac{19}{3}\\-\frac{10}{3}\end{pmatrix}\right|
\\[5pt]
=&\frac{2}{3} \cdot \sqrt{750}
\\[5pt]
\approx&18,26
\end{array}\)](https://mathjax.schullv.de/ab05b5450e777a9cbb35dc254e9fff60ec0d0360cd817321986c70e541a8f4aa?color=5a5a5a) Also beträgt die Länge des Streckenzugs
Also beträgt die Länge des Streckenzugs  etwa
etwa  [LE].
c)(3)
[LE].
c)(3)
 Aussage begründen
Nutze die Ebene
Aussage begründen
Nutze die Ebene  , die durch die Punkte
, die durch die Punkte  ,
,  und
und  bestimmt ist, und eine Symmetrieebene der Pyramide ist. Aufgrund dieser Symmetrie besitzt ein zu
bestimmt ist, und eine Symmetrieebene der Pyramide ist. Aufgrund dieser Symmetrie besitzt ein zu  entsprechender Streckenzug
entsprechender Streckenzug  , der über die Dreiecksflächen
, der über die Dreiecksflächen  und
und  verläuft, dieselbe Länge.
verläuft, dieselbe Länge.  liegt dabei entsprechend auf der Kante
liegt dabei entsprechend auf der Kante  . Also ist
. Also ist  ebenso ein kürzester Weg über die Mantelfläche der Pyramide.
ebenso ein kürzester Weg über die Mantelfläche der Pyramide.
 Koordinaten von
Koordinaten von  bestimmen
Da die Ebene
bestimmen
Da die Ebene  senkrecht zur
senkrecht zur  -
- -Ebene steht, liegt
-Ebene steht, liegt  in „gleicher Höhe über der Grundfläche“ wie
in „gleicher Höhe über der Grundfläche“ wie  , d.h. die
, d.h. die  -Koordinaten der beiden Punkte stimmen überein.
Also ist
-Koordinaten der beiden Punkte stimmen überein.
Also ist  der Schnittpunkt der Geraden durch die Punkte
der Schnittpunkt der Geraden durch die Punkte  und
und  mit der Ebene, die die Koordinatengleichung
mit der Ebene, die die Koordinatengleichung  besitzt. Das Berechnen dieses Schnittpunkts liefert dir
besitzt. Das Berechnen dieses Schnittpunkts liefert dir  .
Die Geradengleichung der Geraden durch die Punkte
.
Die Geradengleichung der Geraden durch die Punkte  und
und  erhältst du, indem du
erhältst du, indem du  als Stützvektor und
als Stützvektor und  als Richtungsvektor wählst:
als Richtungsvektor wählst:
 .
Für einen Schnittpunkt der Geraden
.
Für einen Schnittpunkt der Geraden  und der Ebene mit Koordinatengleichung
und der Ebene mit Koordinatengleichung  muss gelten:
muss gelten:
 .
Einsetzen von
.
Einsetzen von  in die Geradengleichung
in die Geradengleichung  liefert die Koordinaten von
liefert die Koordinaten von  :
:
 .
Damit lauten die Koordinaten von
.
Damit lauten die Koordinaten von  :
:  und
und  .
.

a)(1)
 Zeigen, dass
Zeigen, dass  ein Quadrat ist
Hier ist es deine Aufgabe zu zeigen, dass das Viereck
ein Quadrat ist
Hier ist es deine Aufgabe zu zeigen, dass das Viereck  ein Quadrat ist. Die Punkte
ein Quadrat ist. Die Punkte  ,
,  ,
,  und
und  liegen dabei in der
liegen dabei in der  -
- -Ebene. Also musst du Folgendes tun:
-Ebene. Also musst du Folgendes tun:
 ein Quadrat ist.
1. Schritt: Verbindungsvektoren berechnen
Die Seiten des Vierecks sind hier die Strecken
ein Quadrat ist.
1. Schritt: Verbindungsvektoren berechnen
Die Seiten des Vierecks sind hier die Strecken  ,
,  ,
,  und
und  . Berechne die dazugehörigen Verbindungsvektoren:
. Berechne die dazugehörigen Verbindungsvektoren:



 Damit sind insbesondere die gegenüberliegenden Seiten
Damit sind insbesondere die gegenüberliegenden Seiten  und
und  , sowie
, sowie  und
und  gleich lang.
2. Schritt: Zeigen, dass alle Seiten gleich lang sind
Im 1. Schritt hast du bereits gezeigt, dass die gegenüberliegenden Seiten gleich lang sind. Nun musst du nur noch zeigen, dass zwei anliegende Seiten gleich lang sind. Ist dies der Fall, so sind alle Seiten gleich lang. Zeige also, dass
gleich lang.
2. Schritt: Zeigen, dass alle Seiten gleich lang sind
Im 1. Schritt hast du bereits gezeigt, dass die gegenüberliegenden Seiten gleich lang sind. Nun musst du nur noch zeigen, dass zwei anliegende Seiten gleich lang sind. Ist dies der Fall, so sind alle Seiten gleich lang. Zeige also, dass  . Den Vektorbetrag kannst du mit dem norm-Befehl deines CAS berechnen. Den Befehl für Vektoren findest du unter
keyboard
. Den Vektorbetrag kannst du mit dem norm-Befehl deines CAS berechnen. Den Befehl für Vektoren findest du unter
keyboard  2D
2D  Calc
Calc


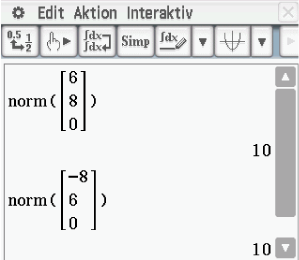 Somit sind alle Seiten gleich lang.
3. Schritt: Zeigen, dass jeder Innenwinkel ein rechter Winkel ist
Hier reicht es zu zeigen, dass ein Innenwinkel 90° ist. Da alle Seiten des Vierecks gleich lang sind, kannst du daraus folgern, dass alle Innenwinkel rechte Winkel sind. Dies kannst du mit dem Skalarpodukt zeigen. Ist das Skalarprodukt zweier Vektoren gleich Null, so stehen die Vektoren senkrecht aufeinander. Berechne also
Somit sind alle Seiten gleich lang.
3. Schritt: Zeigen, dass jeder Innenwinkel ein rechter Winkel ist
Hier reicht es zu zeigen, dass ein Innenwinkel 90° ist. Da alle Seiten des Vierecks gleich lang sind, kannst du daraus folgern, dass alle Innenwinkel rechte Winkel sind. Dies kannst du mit dem Skalarpodukt zeigen. Ist das Skalarprodukt zweier Vektoren gleich Null, so stehen die Vektoren senkrecht aufeinander. Berechne also  . Hierzu kannst du den dotP-Befehl deines CAS verwenden.
. Hierzu kannst du den dotP-Befehl deines CAS verwenden.

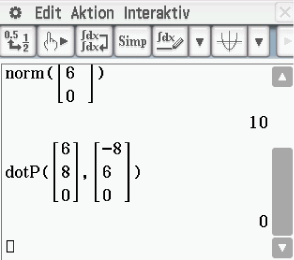 Damit hast du gezeigt, dass alle Innenwinkel des Vierecks rechte Winkel sind. Für das Viereck
Damit hast du gezeigt, dass alle Innenwinkel des Vierecks rechte Winkel sind. Für das Viereck  hast du nun alle 3 Bedingungen gezeigt, also ist
hast du nun alle 3 Bedingungen gezeigt, also ist  ein Quadrat.
a)(2)
ein Quadrat.
a)(2)
 Oberfläche der Pyramide berechnen
Der Flächeninhalt der Oberfläche
Oberfläche der Pyramide berechnen
Der Flächeninhalt der Oberfläche  ist durch eine Formel gegeben:
ist durch eine Formel gegeben:
 Hier ist
Hier ist  der Flächeninhalt der Grundfläche der Pyramide,
der Flächeninhalt der Grundfläche der Pyramide,  ist der Flächeninhalt der Mantelfläche der Pyramide.
Die Grundfläche der Pyramide hat gerade die Form eines Quadrats. Die Länge der Seiten der Grundfläche hast du bereits in (1) berechnet. Also kannst du
ist der Flächeninhalt der Mantelfläche der Pyramide.
Die Grundfläche der Pyramide hat gerade die Form eines Quadrats. Die Länge der Seiten der Grundfläche hast du bereits in (1) berechnet. Also kannst du  folgendermaßen berechnen:
folgendermaßen berechnen:
 Die Mantelfläche der Pyramide setzt sich aus den vier Seitendreiecken zusammen und entsprechendes gilt daher auch für den Flächeninhalt der Mantelfläche. Du kannst verwenden, dass die Seitendreiecke kongruent sind, also sind ihre Flächen gleich groß. Für den Flächeninhalt
Die Mantelfläche der Pyramide setzt sich aus den vier Seitendreiecken zusammen und entsprechendes gilt daher auch für den Flächeninhalt der Mantelfläche. Du kannst verwenden, dass die Seitendreiecke kongruent sind, also sind ihre Flächen gleich groß. Für den Flächeninhalt  eines Seitendreiecks ist der Flächeninhalt der Mantelfläche durch folgende Formel gegeben:
eines Seitendreiecks ist der Flächeninhalt der Mantelfläche durch folgende Formel gegeben:
 Berechne also zuerst den Flächeninhalt eines Seitendreiecks. Wähle das Seitendreieck
Berechne also zuerst den Flächeninhalt eines Seitendreiecks. Wähle das Seitendreieck  . Du benötigst nun die Höhe und die Länge der Grundseite des Dreiecks
. Du benötigst nun die Höhe und die Länge der Grundseite des Dreiecks  . Wähle als Grundseite des Dreiecks die Seite
. Wähle als Grundseite des Dreiecks die Seite  . Mit der Höhe
. Mit der Höhe  des Dreiecks kannst du die Fläche des Dreiecks folgendermaßen berechnen:
des Dreiecks kannst du die Fläche des Dreiecks folgendermaßen berechnen:
 Du musst noch die Höhe
Du musst noch die Höhe  berechnen. Betrachte dazu die untenstehende Skizze:
berechnen. Betrachte dazu die untenstehende Skizze:
 Das Dreieck mit den Eckpunkten
Das Dreieck mit den Eckpunkten  ist rechtwinklig und die Strecke zwischen
ist rechtwinklig und die Strecke zwischen  und
und  entspricht der Höhe
entspricht der Höhe  . Also kannst du die Höhe
. Also kannst du die Höhe  mit dem Satz des Pythagoras berechnen.
mit dem Satz des Pythagoras berechnen.
 ist gerade die Höhe der Pyramide. Da die Grundfläche der Pyramide in der
ist gerade die Höhe der Pyramide. Da die Grundfläche der Pyramide in der  -
- -Ebene liegt, ist die Höhe der Pyramide durch die
-Ebene liegt, ist die Höhe der Pyramide durch die  -Koordinate von
-Koordinate von  gegeben. Also ist
gegeben. Also ist  . Es fehlt nun noch die Länge der Strecke
. Es fehlt nun noch die Länge der Strecke  . Der Punkt
. Der Punkt  ist gerade der Mittelpunkt der Grundfläche. Diese ist quadratisch und somit ist die Länge der Strecke
ist gerade der Mittelpunkt der Grundfläche. Diese ist quadratisch und somit ist die Länge der Strecke  die Hälfte der Länge der Seite
die Hälfte der Länge der Seite  . Also gilt:
. Also gilt:
 Nun kannst du die Höhe
Nun kannst du die Höhe  mit dem Satz des Pythagoras ausrechnen:
mit dem Satz des Pythagoras ausrechnen:
 Also:
Also:  Damit kannst du nun die Oberfläche der Pyramide berechnen:
Damit kannst du nun die Oberfläche der Pyramide berechnen:
![\(\begin{array}[t]{rll}
A&=A_G+A_M& \quad \scriptsize \mid\; A_M=4 \cdot A_\triangle\\[5pt]
&=A_G+4\cdot A_M&\quad \scriptsize \mid\; A_\triangle=\dfrac{1}{2} \cdot h_\triangle \cdot \left|\overrightarrow{OA}\right| \\[5pt]
&=A_G + 4 \cdot \dfrac{1}{2} \cdot h_\triangle \cdot \left|\overrightarrow{OA}\right| \\[5pt]
&=A_G + 2 \cdot h_\triangle \cdot \left|\overrightarrow{OA}\right|
\end{array}\)](https://mathjax.schullv.de/ce842aacdf8df70e6047fabf2fd5b431255eac30a14e32a7815700942186c24b?color=5a5a5a) Hier kannst du die oben berechneten Werte einsetzen:
Hier kannst du die oben berechneten Werte einsetzen:
![\(\begin{array}[t]{rll}
A&=100 + 2 \cdot 11,18 \cdot 10 \\[5pt]
&=100 + 223,6 \\[5pt]
&=323,61
\end{array}\)](https://mathjax.schullv.de/a37dd00c96756a95055860a2027e7d1482f7df362630e404c910a04984ee29c8?color=5a5a5a) Die Oberfläche der Pyramide ist
Die Oberfläche der Pyramide ist  [FE].
[FE].
- Verbindungsvektoren, die die Seiten beschreiben, berechnen.
- Zeige, dass alle Seiten gleich lang sind. Die Länge der Seiten kannst du mit den Beträgen der entsprechenden Verbindungsvektoren berechnen.
- Zeige, dass jeder Innenwinkel ein rechter Winkel ist. Dies kannst du mit dem Skalarprodukt zeigen.



b)(1)
 Parameter- und Koordinatengleichung der Ebene
Parameter- und Koordinatengleichung der Ebene  herleiten
Da du drei Punkte gegeben hast, die in der Ebene
herleiten
Da du drei Punkte gegeben hast, die in der Ebene  liegen, ist es sinnvoll, zunächst die Parameterform der Ebene
liegen, ist es sinnvoll, zunächst die Parameterform der Ebene  zu berechnen. Lege dazu fest, welchen Ortsvektor du als Stützvektor und welche Verbindungsvektoren du als Spannvektoren betrachtest. Diese kannst du dann in die Parameterform einsetzen.
Anschließend kannst du die Parameterform in die gesuchte Koordinatenform umwandeln. Berechne dazu den Normalenvektor
zu berechnen. Lege dazu fest, welchen Ortsvektor du als Stützvektor und welche Verbindungsvektoren du als Spannvektoren betrachtest. Diese kannst du dann in die Parameterform einsetzen.
Anschließend kannst du die Parameterform in die gesuchte Koordinatenform umwandeln. Berechne dazu den Normalenvektor  aus dem Vektorprodukt der beiden Spannvektoren und den Parameter
aus dem Vektorprodukt der beiden Spannvektoren und den Parameter  mit Hilfe einer Punktprobe. Damit erhältst du eine Koordinatengleichung der Ebene
mit Hilfe einer Punktprobe. Damit erhältst du eine Koordinatengleichung der Ebene  durch Einsetzen in die allgemeine Koordinatenform.
1. Schritt: Ebenengleichung in Parameterform aufstellen
Wähle zunächst den Stützvektor und die Spannvektoren:
durch Einsetzen in die allgemeine Koordinatenform.
1. Schritt: Ebenengleichung in Parameterform aufstellen
Wähle zunächst den Stützvektor und die Spannvektoren:
 sei der Stützvektor,
sei der Stützvektor,  und
und  die Spannvektoren.
Du erhältst:
die Spannvektoren.
Du erhältst:


 .
Einsetzen in die Parameterform liefert:
.
Einsetzen in die Parameterform liefert:
 2. Schritt: Parameterform in Koordinatenform umwandeln
Für die Koordinatenform benötigst du zunächst den Normalenvektor
2. Schritt: Parameterform in Koordinatenform umwandeln
Für die Koordinatenform benötigst du zunächst den Normalenvektor  , den du mittels Vektorprodukt der beiden Spannvektoren bestimmen kannst. Anschließend kannst du den Parameter
, den du mittels Vektorprodukt der beiden Spannvektoren bestimmen kannst. Anschließend kannst du den Parameter  mit Hilfe einer Punktprobe bestimmen. Das Kreuzprodukt lässt sich mit dem crossP-Befehl deines CAS berechnen:
mit Hilfe einer Punktprobe bestimmen. Das Kreuzprodukt lässt sich mit dem crossP-Befehl deines CAS berechnen:

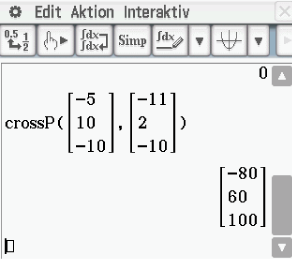 Bestimme den Parameter
Bestimme den Parameter  mit Hilfe einer Punktprobe:
Du weißt bereits, dass
mit Hilfe einer Punktprobe:
Du weißt bereits, dass  aufgrund der Konstruktion in der Ebene
aufgrund der Konstruktion in der Ebene  liegt. Setze also
liegt. Setze also  zusammen mit dem Normalenvektor in die Koordinatenform ein, um den Parameter
zusammen mit dem Normalenvektor in die Koordinatenform ein, um den Parameter  zu ermitteln:
zu ermitteln:
 Einsetzen in die allgemeine Koordinatenform liefert das Ergebnis:
Einsetzen in die allgemeine Koordinatenform liefert das Ergebnis:
![\(\begin{array}{rll}
E: &-80\cdot x_1 + 60\cdot x_2 + 100 \cdot x_3 =1.000 &\scriptsize \mid \ :4
\\[5pt]
E: &-20 \cdot x_1 + 15\cdot x_2 + 25 \cdot x_3 =250
\end{array}\)](https://mathjax.schullv.de/b4f93f06cf63f34cddb0c3ef02a96ba1f4d6c36e47b7ea49ef8a3625ac5866b9?color=5a5a5a) Je nachdem, welche Vektoren als Stütz- und Spannvektoren gewählt wurden, sind noch andere Lösungsansätze möglich.
b)(2)
Je nachdem, welche Vektoren als Stütz- und Spannvektoren gewählt wurden, sind noch andere Lösungsansätze möglich.
b)(2)
 Lage der Punkte
Lage der Punkte  und
und  in jeder Ebene
in jeder Ebene  nachweisen
Führe eine Punktprobe durch, um zu zeigen, dass die Punkte
nachweisen
Führe eine Punktprobe durch, um zu zeigen, dass die Punkte  und
und  in jeder Ebene
in jeder Ebene  liegen. Setze dazu die Koordinaten der Punkte in die allgemeine Koordinatengleichung
liegen. Setze dazu die Koordinaten der Punkte in die allgemeine Koordinatengleichung  ein und zeige, dass diese für alle
ein und zeige, dass diese für alle  erfüllt ist.
erfüllt ist.
 Lage von
Lage von  in jeder Ebene
in jeder Ebene  nachweisen
Einsetzen von
nachweisen
Einsetzen von  in
in  liefert:
liefert:
![\(\begin{array}[t]{rll}
-4\cdot a \cdot (-2) + 3\cdot a \cdot 14 + 25 \cdot 0 =&50\cdot a
\\[5pt]
8\cdot a + 42\cdot a =&50\cdot a
\\[5pt]
50\cdot a =&50\cdot a &\scriptsize \mid\; :50
\\[5pt]
a =& a
\end{array}\)](https://mathjax.schullv.de/cf76dec661fa15c8875c321e5984e1ad27b5d42feab6c04087b2d7c6b1efec18?color=5a5a5a) Diese Gleichung gilt für alle
Diese Gleichung gilt für alle  , also liegt der Punkt
, also liegt der Punkt  in jeder Ebene
in jeder Ebene  .
.
 Lage von
Lage von  in jeder Ebene
in jeder Ebene  nachweisen
Einsetzen von
nachweisen
Einsetzen von  in
in  liefert:
liefert:
![\(\begin{array}[t]{rll}
-4\cdot a \cdot (-8) + 3\cdot a \cdot 6 + 25 \cdot 0 =&50\cdot a
\\[5pt]
32\cdot a + 18\cdot a =&50\cdot a
\\[5pt]
50\cdot a =&50\cdot a &\scriptsize \mid\; :50
\\[5pt]
a =& a
\end{array}\)](https://mathjax.schullv.de/7365156071f53e31989ca8a82f8a66f00f0e203e31b99169bfcb983bb7ef0952?color=5a5a5a) Diese Gleichung gilt für alle
Diese Gleichung gilt für alle  , also liegt der Punkt
, also liegt der Punkt  in jeder Ebene
in jeder Ebene  .
b)(3)
.
b)(3)
 Verschiedene Arten der Schnittgebilde nennen
Im vorigen Aufgabenteil hast du bewiesen, dass die Punkte
Verschiedene Arten der Schnittgebilde nennen
Im vorigen Aufgabenteil hast du bewiesen, dass die Punkte  und
und  in jeder der Ebenen
in jeder der Ebenen  liegen. Damit enthält jede Ebene
liegen. Damit enthält jede Ebene  die Seitenkante
die Seitenkante  der Pyramide. Überlege dir nun, auf welche verschiedenen Arten eine solche Ebene
der Pyramide. Überlege dir nun, auf welche verschiedenen Arten eine solche Ebene  die Pyramide schneiden kann und welche Schnittgebilde daraus entstehen:
die Pyramide schneiden kann und welche Schnittgebilde daraus entstehen:
 Gesuchten Wert von
Gesuchten Wert von  bestimmen
Damit das Schnittgebilde von Ebene und Pyramide ein Dreieck ist, muss das Seitendreieck
bestimmen
Damit das Schnittgebilde von Ebene und Pyramide ein Dreieck ist, muss das Seitendreieck  in der Ebene liegen. Also ist die Ebene
in der Ebene liegen. Also ist die Ebene  gesucht, in der die Punkte
gesucht, in der die Punkte  ,
,  und
und  liegen.
Da
liegen.
Da  und
und  in jeder Ebene liegen, musst du die Ebene
in jeder Ebene liegen, musst du die Ebene  bestimmen, die auch
bestimmen, die auch  enthält. Dazu kannst du die Koordinaten von
enthält. Dazu kannst du die Koordinaten von  in die allgemeine Koordinatengleichung
in die allgemeine Koordinatengleichung  einsetzen und nach
einsetzen und nach  auflösen:
auflösen:
![\(\begin{array}[t]{rll}
-4\cdot a \cdot (-1) + 3\cdot a \cdot 7 + 25 \cdot 10 =&50\cdot a
\\[5pt]
4\cdot a + 21\cdot a + 250 =&50\cdot a & \scriptsize \mid\; - 25\cdot a
\\[5pt]
250 =&25\cdot a & \scriptsize \mid\; : 25
\\[5pt]
10 =&a
\end{array}\)](https://mathjax.schullv.de/e5b519665af247175e46730e2b736d8b9f64ead48e207ff5890826a5f4e8e162?color=5a5a5a) Also ist für
Also ist für  das Schnittgebilde von Ebene und Pyramide das Dreieck
das Schnittgebilde von Ebene und Pyramide das Dreieck  .
b)(5)
.
b)(5)
 Verhältnis der Rauminhalte der beiden Teilkörper bestimmen
Die Ebene
Verhältnis der Rauminhalte der beiden Teilkörper bestimmen
Die Ebene  zerlegt die Pyramide
zerlegt die Pyramide  in eine „kleine“ Pyramide mit Spitze
in eine „kleine“ Pyramide mit Spitze  (oberer Teilkörper) und einen „Restkörper“, was du in folgender Skizze gut erkennen kannst:
(oberer Teilkörper) und einen „Restkörper“, was du in folgender Skizze gut erkennen kannst:
 Um das Verhältnis der Rauminhalte der beiden Körper zu bestimmen, kannst du wie folgt vorgehen:
Um das Verhältnis der Rauminhalte der beiden Körper zu bestimmen, kannst du wie folgt vorgehen:
 Dabei ist
Dabei ist  die Grundfläche der Pyramide und
die Grundfläche der Pyramide und  die Höhe der Pyramide.
1. Schritt: Volumen der Pyramide
die Höhe der Pyramide.
1. Schritt: Volumen der Pyramide  berechnen
Die Grundfläche der Pyramide
berechnen
Die Grundfläche der Pyramide  und die Höhe
und die Höhe  hast du bereits in Aufgabe a) (2) berechnet.
hast du bereits in Aufgabe a) (2) berechnet.
 .
2. Schritt: Volumen der „kleinen“ Pyramide berechnen
Die Grundfläche der „kleinen“ Pyramide
.
2. Schritt: Volumen der „kleinen“ Pyramide berechnen
Die Grundfläche der „kleinen“ Pyramide  ist in der Aufgabenstellung gegeben. Berechne also die Höhe
ist in der Aufgabenstellung gegeben. Berechne also die Höhe  .
Bestimme zunächst die Hesse‘sche Normalenform von der Ebene
.
Bestimme zunächst die Hesse‘sche Normalenform von der Ebene  . Lese dazu den Normalenvektor
. Lese dazu den Normalenvektor
 :
aus der Koordinatengleichung von
:
aus der Koordinatengleichung von  ab und bestimme dessen Länge:
ab und bestimme dessen Länge:
 Damit erhältst du die Hesse‘sche Normalenform von
Damit erhältst du die Hesse‘sche Normalenform von  :
:
 .
Einsetzen von
.
Einsetzen von  in die linke Seite der Hesse‘schen Normalenform von
in die linke Seite der Hesse‘schen Normalenform von  liefert dir den Abstand von
liefert dir den Abstand von  zur Ebene
zur Ebene  , was gerade der gesuchten Höhe entspricht:
, was gerade der gesuchten Höhe entspricht:
 Nun kannst du
Nun kannst du  und
und  in die Formel zum Berechnen des Volumens einer Pyramide einsetzen und erhältst für das Volumen
in die Formel zum Berechnen des Volumens einer Pyramide einsetzen und erhältst für das Volumen  der „kleinen“ Pyramide:
der „kleinen“ Pyramide:
 .
3. Schritt: Volumen des „Restkörpers“ berechnen
Das Volumen
.
3. Schritt: Volumen des „Restkörpers“ berechnen
Das Volumen  des „Restkörpers“ ist die Differenz aus den Volumina der gesamten und der „kleinen“ Pyramide, also:
des „Restkörpers“ ist die Differenz aus den Volumina der gesamten und der „kleinen“ Pyramide, also:
 .
4. Schritt: Verhältnis ermitteln
Setze die beiden errechneten Volumina in Verhältnis zueinander:
.
4. Schritt: Verhältnis ermitteln
Setze die beiden errechneten Volumina in Verhältnis zueinander:
 .
Damit beträgt das Verhältnis von der „kleinen“ Pyramide zum „Restkörper“
.
Damit beträgt das Verhältnis von der „kleinen“ Pyramide zum „Restkörper“  .
.

- Strecke: Die Ebene
schneidet die Pyramide nur in der Seitenkante
.
- Dreieck: Die Ebene
schneidet die Pyramide im Seitendreieck
.
- Quadrat: Die Ebene
schneidet die Pyramide im Viereck
.
- Trapez: Die Ebene
schneidet die Pyramide in der Trapezfläche, die durch
,
und jeweils einen Punkt auf der Seitenkanten
und
definiert ist.

- Bestimme zunächst das Volumen der Pyramide
. Nutze dazu die bereits in Aufgabe a)(2) berechneten Werte für Grundfläche und Höhe der Pyramide.
- Berechne anschließend das Volumen der „kleinen“ Pyramide. Die Höhe der kleinen Pyramide ist der Abstand der Spitze
von der Ebene
, den du über die Hesse‘sche Normalenform berechnen kannst. Die Grundfläche ist in der Aufgabenstellung gegeben.
- Das Volumen des „Restkörpers“ ergibt sich aus der Differenz der „kleinen“ Pyramide und der Pyramide
.
- Damit kannst du dann das Verhältnis der Rauminhalte der beiden Teilkörper ermitteln.
c)(1)
 Koordinaten von
Koordinaten von  bestimmen
Der gesuchte Punkt
bestimmen
Der gesuchte Punkt  soll auf der Geraden
soll auf der Geraden  liegen und erfüllen, dass
liegen und erfüllen, dass  und
und  senkrecht zu
senkrecht zu  sind. Ermittle also eine Geradengleichung von
sind. Ermittle also eine Geradengleichung von  , um die Form der Koordinaten des Punktes
, um die Form der Koordinaten des Punktes  in Abhängigkeit des Parameters der Geradengleichung zu erhalten. Anschließend kannst du den genauen Parameter für
in Abhängigkeit des Parameters der Geradengleichung zu erhalten. Anschließend kannst du den genauen Parameter für  bestimmen, indem du das Skalarprodukt von
bestimmen, indem du das Skalarprodukt von  oder
oder  und dem Richtungsvektor von
und dem Richtungsvektor von  berechnest, das gleich Null sein muss.
Da die Punkte
berechnest, das gleich Null sein muss.
Da die Punkte  und
und  auf der Geraden
auf der Geraden  liegen, kannst du
liegen, kannst du  als Stützvektor der Geraden und den Verbindungsvektor
als Stützvektor der Geraden und den Verbindungsvektor  als Richtungsvektor auffassen. Somit ergibt sich die Geradengleichung
als Richtungsvektor auffassen. Somit ergibt sich die Geradengleichung  :
:
 Also hat ein Punkt
Also hat ein Punkt  auf der Geraden
auf der Geraden  folgende Gestalt:
folgende Gestalt:
 .
Damit
.
Damit  senkrecht zur Geraden
senkrecht zur Geraden  ist, muss das Skalarprodukt aus
ist, muss das Skalarprodukt aus  und dem Richtungsvektor von
und dem Richtungsvektor von  gerade Null ergeben, die daraus resultierende Gleichung kannst du mit dem solve-Befehl deines CAS nach
gerade Null ergeben, die daraus resultierende Gleichung kannst du mit dem solve-Befehl deines CAS nach  lösen:
lösen:
![\(\begin{array}[t]{rll}
\begin{pmatrix} 6-7 \cdot r\\8 - r\\10 \cdot r\end{pmatrix} \circ \begin{pmatrix}-7\\-1\\10\end{pmatrix} \stackrel{!}{=}&0
\\[5pt]
r =& \dfrac{1}{3}
\end{array}\)](https://mathjax.schullv.de/2dbc0e91a7dd2293550d658193b6846e076566b7bcb53ef8ffb8109e088c76c4?color=5a5a5a)
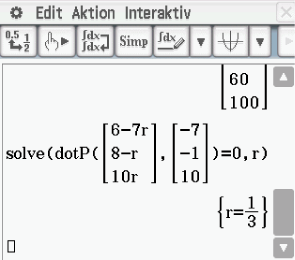 Einsetzen von
Einsetzen von  in die Koordinaten von
in die Koordinaten von  ergibt:
ergibt:
 Da man nur eine mögliche Lösung erhält, sind dies die gesuchten Koordinaten von
Da man nur eine mögliche Lösung erhält, sind dies die gesuchten Koordinaten von  . Also lauten die Koordinaten
. Also lauten die Koordinaten  .
c)(2)
.
c)(2)

 als einen kürzesten Weg begründen
Ein kürzester Weg von einem Punkt zu einer Geraden ist das Lot vom Punkt auf die Gerade. Nutze diese Eigenschaft, um die Behauptung zu begründen.
Zunächst gilt, dass der Punkt
als einen kürzesten Weg begründen
Ein kürzester Weg von einem Punkt zu einer Geraden ist das Lot vom Punkt auf die Gerade. Nutze diese Eigenschaft, um die Behauptung zu begründen.
Zunächst gilt, dass der Punkt  auf der Seitenkante
auf der Seitenkante  liegt:
liegt:

 ist Fußpunkt des Lotes von
ist Fußpunkt des Lotes von  auf
auf  sowie des Lotes von
sowie des Lotes von  auf
auf  , was du im vorigen Aufgabenteil bewiesen hast (
, was du im vorigen Aufgabenteil bewiesen hast ( und
und  sind senkrecht zu
sind senkrecht zu  ). Damit ist
). Damit ist  der kürzeste Weg von
der kürzeste Weg von  zur Geraden
zur Geraden  und
und  der kürzeste Weg von
der kürzeste Weg von  zur Geraden
zur Geraden  . Deswegen ist der Streckenzug
. Deswegen ist der Streckenzug  der kürzeste Weg von
der kürzeste Weg von  nach
nach  über die Dreiecksflächen
über die Dreiecksflächen  und
und  .
Da die Ebene
.
Da die Ebene  , die durch die Punkte
, die durch die Punkte  ,
,  und
und  bestimmt ist, eine Symmetrieebene der Pyramide ist (
bestimmt ist, eine Symmetrieebene der Pyramide ist ( teilt die Pyramide in zwei symmetrische Teilkörper), gibt es keinen kürzeren Weg über die Dreiecksflächen
teilt die Pyramide in zwei symmetrische Teilkörper), gibt es keinen kürzeren Weg über die Dreiecksflächen  und
und  .
.
 Länge des Streckenzugs berechnen
Berechne die Länge des Streckenzugs
Länge des Streckenzugs berechnen
Berechne die Länge des Streckenzugs  als Summe der Länge der Vektoren
als Summe der Länge der Vektoren  und
und  .
.
![\(\begin{array}[t]{rll}
\left|\overline{OPB}\right|=& \left|\overrightarrow{OP}\right| + \left|\overrightarrow{BP}\right|
\\[5pt]
=&\left|\begin{pmatrix} \frac{11}{3}\\\frac{23}{3}\\\frac{10}{3}\end{pmatrix}\right| + \left|\begin{pmatrix} -\frac{17}{3}\\\frac{19}{3}\\-\frac{10}{3}\end{pmatrix}\right|
\\[5pt]
=&\frac{2}{3} \cdot \sqrt{750}
\\[5pt]
\approx&18,26
\end{array}\)](https://mathjax.schullv.de/ab05b5450e777a9cbb35dc254e9fff60ec0d0360cd817321986c70e541a8f4aa?color=5a5a5a) Also beträgt die Länge des Streckenzugs
Also beträgt die Länge des Streckenzugs  etwa
etwa  [LE].
c)(3)
[LE].
c)(3)
 Aussage begründen
Nutze die Ebene
Aussage begründen
Nutze die Ebene  , die durch die Punkte
, die durch die Punkte  ,
,  und
und  bestimmt ist, und eine Symmetrieebene der Pyramide ist. Aufgrund dieser Symmetrie besitzt ein zu
bestimmt ist, und eine Symmetrieebene der Pyramide ist. Aufgrund dieser Symmetrie besitzt ein zu  entsprechender Streckenzug
entsprechender Streckenzug  , der über die Dreiecksflächen
, der über die Dreiecksflächen  und
und  verläuft, dieselbe Länge.
verläuft, dieselbe Länge.  liegt dabei entsprechend auf der Kante
liegt dabei entsprechend auf der Kante  . Also ist
. Also ist  ebenso ein kürzester Weg über die Mantelfläche der Pyramide.
ebenso ein kürzester Weg über die Mantelfläche der Pyramide.
 Koordinaten von
Koordinaten von  bestimmen
Da die Ebene
bestimmen
Da die Ebene  senkrecht zur
senkrecht zur  -
- -Ebene steht, liegt
-Ebene steht, liegt  in „gleicher Höhe über der Grundfläche“ wie
in „gleicher Höhe über der Grundfläche“ wie  , d.h. die
, d.h. die  -Koordinaten der beiden Punkte stimmen überein.
Also ist
-Koordinaten der beiden Punkte stimmen überein.
Also ist  der Schnittpunkt der Geraden durch die Punkte
der Schnittpunkt der Geraden durch die Punkte  und
und  mit der Ebene, die die Koordinatengleichung
mit der Ebene, die die Koordinatengleichung  besitzt. Das Berechnen dieses Schnittpunkts liefert dir
besitzt. Das Berechnen dieses Schnittpunkts liefert dir  .
Die Geradengleichung der Geraden durch die Punkte
.
Die Geradengleichung der Geraden durch die Punkte  und
und  erhältst du, indem du
erhältst du, indem du  als Stützvektor und
als Stützvektor und  als Richtungsvektor wählst:
als Richtungsvektor wählst:
 .
Für einen Schnittpunkt der Geraden
.
Für einen Schnittpunkt der Geraden  und der Ebene mit Koordinatengleichung
und der Ebene mit Koordinatengleichung  muss gelten:
muss gelten:
 .
Einsetzen von
.
Einsetzen von  in die Geradengleichung
in die Geradengleichung  liefert die Koordinaten von
liefert die Koordinaten von  :
:
 .
Damit lauten die Koordinaten von
.
Damit lauten die Koordinaten von  :
:  und
und  .
.
