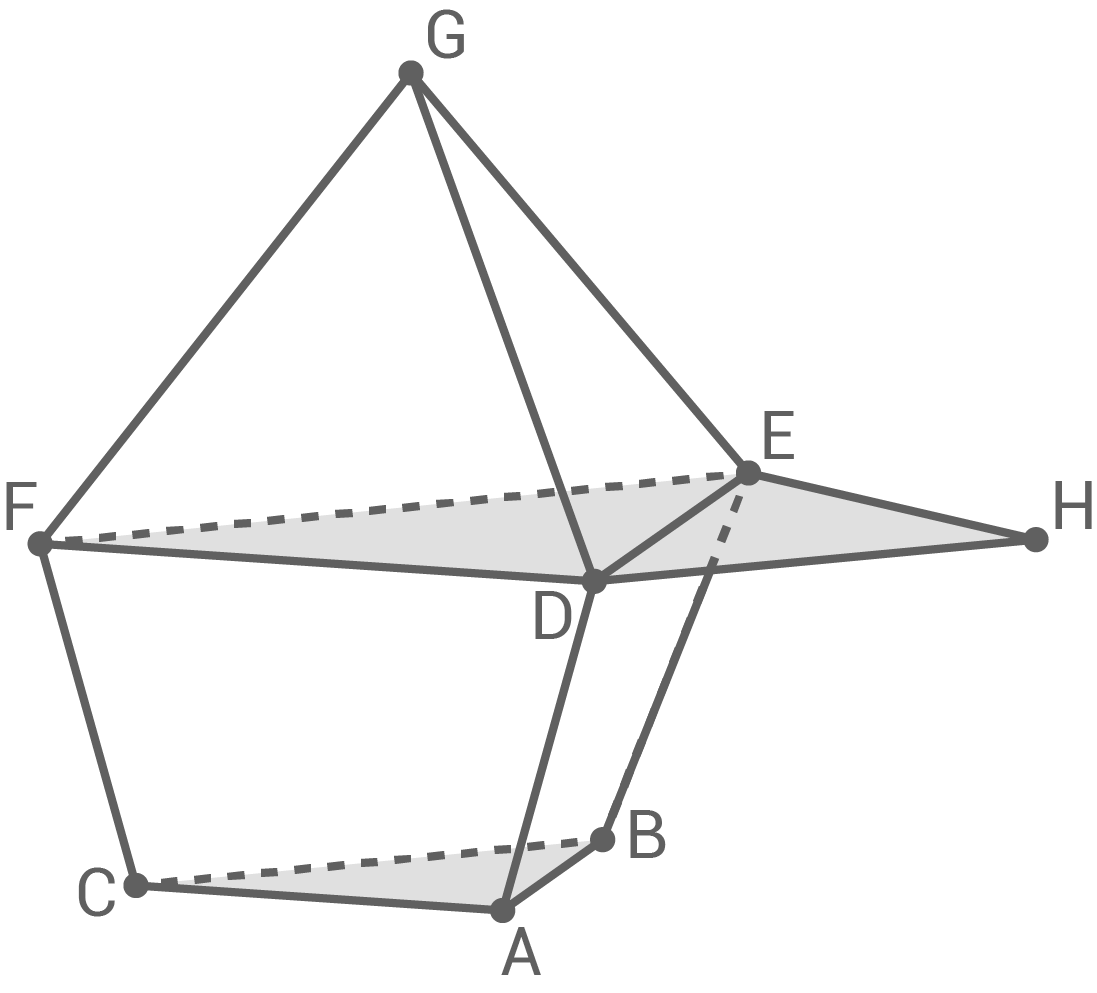
Aufgabe 3

Das Gebäude eines Museums kann modellhaft durch den abgebildeten Körper $ABCDEFG$ dargestellt werden.
Die obere Etage des Museums entspricht dabei der Pyramide $DEFG,$ die untere Etage dem Körper $ABCDEF,$ der Teil der Pyramide $DEFS$ ist.
Die Ebene, in der das Dreieck $ABC$ liegt, beschreibt die horizontale Oberfläche des Untergrunds. Das Dreieck $DEF$ liegt parallel zu dieser Ebene.
In einem kartesischen Koordinatensystem gilt für die Lage einiger der genannten Punkte:

$A(-5\mid 5\mid 0),$ $B(-5\mid 25\mid 0),$ $D(0\mid 0\mid 15),$ $E(0\mid 30\mid 15),$ $F(-25\mid 5\mid 15)$ und $G(-10\mid 10\mid 35).$

Eine Längeneinheit im Koordinatensystem entspricht $1\,\text{m}$ in der Realität.

Geometrische Darstellung mit verschiedenen Punkten und Flächen in einem 3D-Raum.

Abbildung 1

Die folgenden Rechnungen zeigen ein mögliches Vorgehen zur Ermittlung der Koordinaten von $S:$

Rechnung anzeigen

d.h. $S(-15\mid 15\mid -30)$

Erläutere das dargestellte Vorgehen.

(5 Punkte)

(1)

Weise nach, dass die Bodenfläche $DEF$ der oberen Etage nicht rechtwinklig ist.

(4 Punkte)

$\,$

(2)

Bestimme für das Dreieck $DEF$ die Größe des Innenwinkels $\epsilon$ bei $E$ sowie die Länge der Höhe $h$ zur Seite $\overline{EF}.$

[Zur Kontrolle: $\epsilon = 45^{\circ};$ $h=15\sqrt{2}$ ]

(5 Punkte)

$\,$

(3)

Begründe, dass der Abstand des Punktes $G$ zur Ebene durch $DEF$ direkt aus den Koordinaten der entsprechenden Punkte ermittelt werden kann, und gib diesen Abstand an.

(2 Punkte)

$\,$

(4)

Für die obere Etage wird eine Anlage zur Entfeuchtung der Luft installiert, die für $100\,\text{m}^3$ Rauminhalt eine elektrische Leistung von $0,8$ Kilowatt benötigt.
Weise nach, dass für den Betrieb der Anlage eine Leistung von $25$ Kilowatt ausreichend ist.

(4 Punkte)

(1)

Weise nach, dass die Gerade $AG$ und die Ebene, in der das Dreieck $DEF$ liegt, sich im Punkt $R\left(-\frac{50}{7}\mid \frac{50}{7}\mid 15\right)$ schneiden.

(4 Punkte)

$\,$

(2)

Bestimme eine Koordinatenform der Ebene $U,$ in der das Dreieck $EFG$ liegt.

[Zur Kontrolle: $U:\, 2x_1-2x_2-x_3 = -75.$ ]

(3 Punkte)

$\,$

(3)

An einer Metallstange, die durch die Strecke $\overline{RG}$ dargestellt wird, ist im Punkt $Q$ ein Scheinwerfer befestigt, dessen Größe vernachlässigt werden soll. Der Scheinwerfer beleuchtet aus einer Entfernung von $5\,\text{m}$ diejenige Wand, die im Modell durch das Dreieck $EFG$ dargestellt wird.
Zeige, dass der Punkt $Q$ mit den Koordinaten $Q\left(-\frac{95}{11}\mid \frac{95}{11}\mid \frac{280}{11}\right)$ auf der Strecke $\overline{RG}$ liegt und einen Abstand von $5\,\text{m}$ zur Ebene $U$ hat.

(8 Punkte)

Der seitliche Eingang des Museums wird durch das Viereck $ABED$ modelliert. Der Architekt plant fr diesen Bereich eine dreieckige Überdachung. Eine mögliche Überdachung wird durch das Dreieck $DHE$ modelliert. Diese Überdachung ist in der Abbildung 2, allerdings von einer anderen Seitenansicht als in der Abbildung 1, dargestellt.

Abbildung 2

Die Planung sieht vor, dass das Dreieck $DEH$ in der gleichen Ebene wie das Dreieck $DEF$ liegt. Des Weiteren sollen die Koordinaten des Punktes $H$ so gewählt werden, dass das Dreieck $DEH$ ein gleichschenkliges Dreieck mit der Basis $\overline{DE}$ ist.
Beurteile die Aussage, dass der Ortsvektor des Punktes $H$ folgende Gleichung erfüllt:

$\overline{OH}$ $= \pmatrix{0\\15\\15} + a\cdot \pmatrix{1\\0\\0}$ $= \pmatrix{a\\15\\15};$ $a\in \mathbb{R}.$

(5 Punkte)

$\blacktriangleright$ Vorgehen beschreiben

Der Punkt $S$ ist der Schnittpunkt der drei Geraden durch die Punkte $F$ und $C,$ $D$ und $A,$ $E$ und $B.$

Es genügt den Schnittpunkt zweier Geraden zu bestimmen. In der dargestellten Rechnung werden die beiden Parameterdarstellungen der Geraden durch die Punkte $D$ und $A$ mit dem Geradenparameter $r$ und durch die Punkte $E$ und $B$ mit dem Geradenparameter $s$ gleichgesetzt.
Diese Gleichung liefert eine Lösung für $r$ und $s.$ Der Wert für $r$ wird in die Geradengleichung durch die Punkte $D$ und $A$ eingesetzt und liefert den Ortsvektor des Schnittpunkts.
Daraus erhält man die Koordinaten des Punkts $S.$

(1)

$\blacktriangleright$ Nachweisen, dass die Bodenfläche nicht rechtwinklig ist

Die Bodenfläche $DEF$ ist rechtwinklig, wenn es zwei Verbindungsvektoren der Eckpunkte gibt, die senkrecht aufeinander stehen. Das ist der Fall, wenn ihr Skalarprodukt Null ist.

$\begin{array}[t]{rll} \overrightarrow{DE}\circ \overrightarrow{DF}& \neq 0 \\[10pt] \overrightarrow{DE}\circ \overrightarrow{EF}&\neq 0 \\[10pt] \overrightarrow{DF}\circ \overrightarrow{EF}& \neq 0 \\[10pt] \end{array}$