Vektorielle Geometrie

Gegeben sind das gerade Prisma $ABCDEF$ mit den Eckpunkten $C(0\mid0\mid 0),$ $D(6\mid0\mid 5),$ $E(0\mid8\mid5)$ und $F(0\mid0\mid 5)$ sowie der Punkt $M(3\mid4\mid 5)$ (vgl. Abbildung 1).

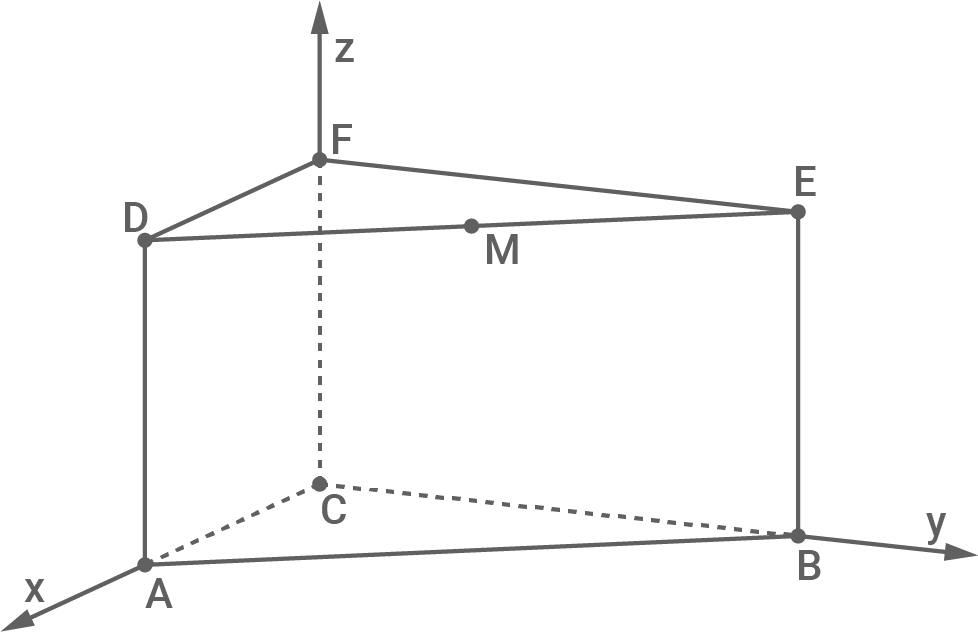
Abb. 1

(1)

Berechne die Größe des Innenwinkels des Dreiecks $DEF$ bei $D.$

(2)

Berechne den Inhalt der Oberfläche des Prismas.

(2 + 4 Punkte)

(1)

Mit $W_t$ wird die Ebene bezeichnet, die die Punkte $M, F$ und $S_t(t\mid0\mid 0)$ mit $t\geq0$ enthält.

In Abbildung 2 ist dieser Sachverhalt für einen bestimmten Wert von $t$ dargestellt.

Abb. 2

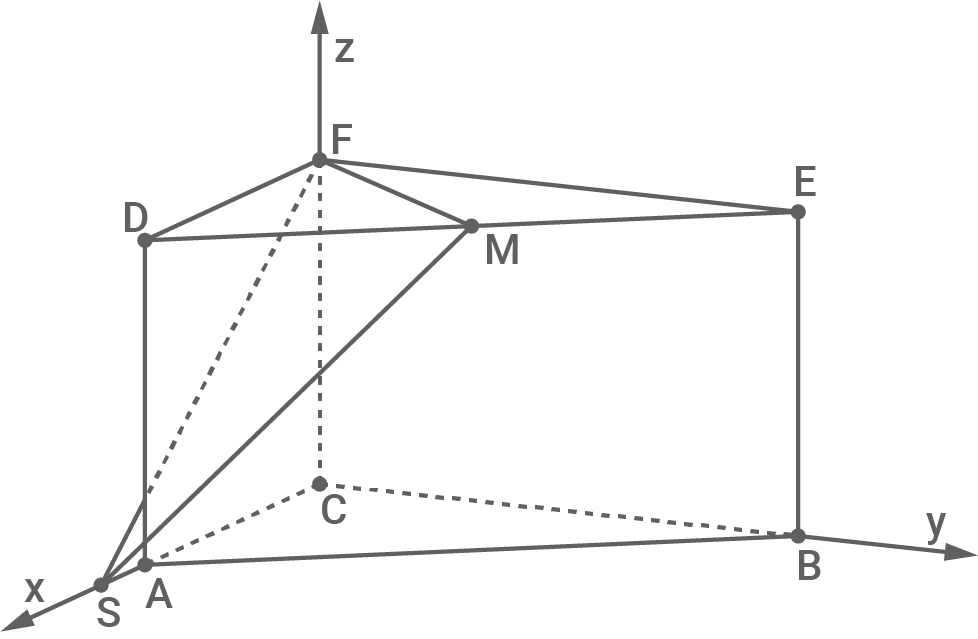Stelle eine Gleichung der Ebene $W_t$ in Parameterform auf.

(2)

Bestimme die Koordinaten eines Normalenvektors der Ebene $W_t.$

[Zur Kontrolle: $\pmatrix{20\\-15\\4t}$ ist ein Normalenvektor der Ebene $W_t.$ ]

(3)

Berechne die Größe des Winkels zwischen der Ebene $W_5$ und der $x$ - $y$ -Ebene.

(4)

Untersuche, ob es einen Wert von $t$ gibt, für den die Strecke $\overline{BD}$ senkrecht zur Ebene $W_t$ verläuft.

(5)

Die Gerade $g_t$ verläuft durch den Punkt $D$ und senkrecht zur Ebene $W_t$ . Für $t\gt0$ schneidet die Gerade $g_t$ die $x$ - $y$ -Ebene im Punkt $Q_t.$

Bestimme die Koordinaten des Punktes $Q_t$ .

[Zur Kontrolle: $Q_t\left(6-\frac{25}{t}\left\vert\frac{75}{4 \cdot t}\right\vert 0\right)$ ]

(6)

Im Folgenden sind drei Schritte der Lösung einer Aufgabe angegeben, die im Zusammenhang mit den betrachteten geometrischen Objekten steht:

$(\text{I})$

$P(6-6 \cdot r\mid 8 \cdot r\mid 0)$ mit $0 \leq r \leq 1.$

$(\text{II})$

$\left|\begin{array}{rl} 6-\dfrac{25}{t} \; & =\quad6-6 \cdot r \\ \dfrac{75}{4 \cdot t} \; & =\quad8 \cdot r \end{array}\right|$

$(\text{III})$

Das Gleichungssystem $(\text{II})$ besitzt keine Lösung.

Gib eine passende Aufgabenstellung an und interpretiere $(\text{III})$ geometrisch.

(2 + 3 + 3 + 4 + 4 + 3 Punkte)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

(1)

Für die Vektoren $\overrightarrow{DF}$ und $\overrightarrow{DE}$ folgt:

$\overrightarrow{DF} = \pmatrix{0-6 \\ 0-0 \\ 5-5} = \pmatrix{-6 \\ 0 \\ 0}$

$\overrightarrow{DE} = \pmatrix{0-6 \\ 8-0 \\ 5-5} = \pmatrix{-6 \\ 8 \\ 0}$

Für den gesuchten Winkel folgt mit dem CAS:

$\begin{array}[t]{rll} \cos(\alpha)&=&\dfrac{\left\vert\overrightarrow{DF} \circ \overrightarrow{DE}\right\vert}{\left\vert\overrightarrow{DF}\right\vert \cdot \left\vert\overrightarrow{DE}\right\vert} \\[5pt] \cos(\alpha)&=&\dfrac{36}{\sqrt{36} \cdot \sqrt{100}} \\[5pt] \alpha&\approx&53,13^\circ \end{array}$

(2)

Die Oberfläche des Prismas besteht aus zwei Dreiecken und drei Rechtecken.

1. Schritt: Flächeninhalt der Dreiecke berechnen

Da sich der Punkt $F$ jeweils nur in einer Koordinate von den Punkten $D$ und $E$ unterscheidet, ergeben sich die Längen der Seiten, die den rechten Winkel einschließen, direkt als $6\;\text{LE}$ und $8\;\text{LE}.$ Somit folgt für den Flächeninhalt beider Dreiecke zusammen:

$\begin{array}[t]{rll} A_D&=&2\cdot\dfrac{1}{2}\cdot6\cdot8 \\[5pt] &=&48\;[\text{FE}] \end{array}$

2. Schritt: Flächeninhalt der Rechtecke berechnen

Anhand der Koordinaten der Punkte $C$ und $F$ lässt sich ablesen, dass das Prisma eine Höhe von $5\;\text{LE}$ besitzt. Die fehlenden Seitenlängen der drei Rechtecke sind jeweils durch die Länge einer der Seiten des Dreiecks $DFE$ gegeben. Somit folgt mit dem Satz des Pythagoras für die Summe der Flächeninhalte aller Rechtecke:

$\begin{array}[t]{rll} A_R&=&5\cdot\left(6+8+\sqrt{6^2+8^2}\right) \\[5pt] &=&120\;[\text{FE}] \end{array}$

Für den Inhalt der Oberfläche des Prismas folgt somit insgesamt:

$\begin{array}[t]{rll} A_O&=&A_D+A_R \\[5pt] &=&48+120 \\[5pt] &=&168\;[\text{FE}] \end{array}$

(1)

Für die beiden Vektoren $\overrightarrow{S_tM}$ und $\overrightarrow{S_tF}$ gilt:

$\overrightarrow{S_tM} = \pmatrix{3-t \\ 4-0 \\ 5-0} = \pmatrix{3-t \\ 4 \\ 5}$

$\overrightarrow{S_tF} = \pmatrix{0-t \\ 0-0 \\ 5-0} = \pmatrix{-t \\ 0 \\ 5}$

Mit dem Ortsvektor von $S_t$ als Stützvektor und den beiden eben berechneten Vektoren als Spannvektoren folgt:

$W_t:\overrightarrow{x} = \pmatrix{t \\ 0 \\ 0} + r \cdot \pmatrix{3-t \\ 4 \\ 5}$ $+ s \cdot \pmatrix{-t \\ 0 \\ 5}$

(2)

$\begin{array}[t]{rll} \overrightarrow{n}&=&\pmatrix{3-t \\ 4 \\ 5}\times\pmatrix{-t \\ 0 \\ 5} \\[5pt] &=&\pmatrix{4\cdot5-5\cdot0 \\ 5\cdot(-t)-(3-t)\cdot5 \\ (3-t)\cdot0-4\cdot(-t)} \\[5pt] &=&\pmatrix{20 \\ -15 \\ 4t} \end{array}$

(3)

Ein Normalenvektor der $x$ - $y$ -Ebene ist $\overrightarrow{n_{xy}} = \pmatrix{0 \\ 0 \\ 1}.$ Damit folgt für den gesuchten Winkel mit dem CAS:

$\begin{array}[t]{rll} \cos(\alpha)&=&\dfrac{\left\vert\overrightarrow{n} \circ \overrightarrow{n_{xy}}\right\vert}{\left\vert\overrightarrow{n}\right\vert \cdot \left\vert\overrightarrow{n_{xy}}\right\vert} \\[5pt] \cos(\alpha)&=&\dfrac{20}{\sqrt{1025}} \\[5pt] \alpha&\approx&51,34^\circ \end{array}$

(4)

Anhand der Skizze des Prismas ergeben sich die Koordinaten $B(0\mid8\mid0).$ Für den Vektor $\overrightarrow{BD}$ folgt somit:

$\overrightarrow{BD} = \pmatrix{6-0 \\ 0-8 \\ 5-0} = \pmatrix{6 \\ -8 \\ 5}$

Damit die Strecke $\overline{BD}$ für einen Wert von $t$ senkrecht zu $W_t$ verläuft, muss ein $t\geq0$ und eine Zahl $r$ existieren, sodass $r\cdot\overrightarrow{BD}=\overrightarrow{n}$ gilt. Die erste Koordinate liefert hierbei $r=\frac{20}{6}=\frac{10}{3}.$ Einsetzen in die zweite Koordinate liefert allerdings $-8\cdot\frac{10}{3}=-\frac{80}{3}\neq-15.$ Somit existiert kein Wert von $t,$ für den die Strecke $\overline{BD}$ senkrecht zu $W_t$ verläuft.

(5)

Für $g_t$ ergibt sich folgende Geradengleichung:

$g_t:\overrightarrow{x}=\pmatrix{6 \\ 0 \\ 5}+s\cdot\pmatrix{20 \\ -15 \\ 4t}$

Einsetzen der Koordinaten $(6+20s\mid-15s\mid5+4st)$ eines allgemeinen Punktes auf $g_t$ in die Ebenengleichung $z=0$ der $x$ - $y$ -Ebene liefert:

$\begin{array}[t]{rll} 5+4st&=&0 &\quad \scriptsize \mid\;-5 \\[5pt] 4st&=&-5 &\quad \scriptsize \mid\;:4t \\[5pt] s&=&-\dfrac{5}{4t} \end{array}$

Einsetzen von $s=-\frac{5}{4t}$ in die Geradengleichung von $g_t$ liefert:

$\pmatrix{6 \\ 0 \\ 5}-\dfrac{5}{4t}\cdot\pmatrix{20 \\ -15 \\ 4t} = \pmatrix{6-\frac{25}{t} \\ \frac{75}{4t} \\ 0}$

Für die Koordinaten des Punktes $Q_t$ folgt damit $Q_t\left(6-\dfrac{25}{t}\,\bigg \vert \,\dfrac{75}{4t}\,\bigg \vert \,0\right).$

(6)

Passende Aufgabenstellung angeben

„Zeige, dass es keinen Wert für $t$ gibt, sodass der Punkt $Q_t$ auf der Strecke $\overline{AB}$ liegt.”

Gleichung $\boldsymbol{\text{III}}$ geometrisch interpretieren

Es gibt keinen Wert von $t,$ sodass die Gerade $g_t$ vollständig in der durch die Seitenfläche $ABDE$ aufgespannten Ebene liegt.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?