Teil A: Ohne Hilfsmittel

Gegeben ist die Funktion $f$ mit $f(x)=x\cdot(x^2-1),$ $x\in\mathbb{R}.$

(1)

Zeige: $\(f$

(2)

Bestimme eine Gleichung der Tangente an den Graphen von $f$ an der Stelle $x=-\dfrac{1}{2}.$

(3 + 3 Punkte)

Eine Funktionenschar $f_k$ ist gegeben durch $f_k(x)=\mathrm e ^{-x}-k$ für $x\in\mathbb{R},$ $k\in\mathbb{R},$ $k \gt 0.$

(1)

Bestimme $k$ so, dass $x=-1$ eine Nullstelle von $f_k$ ist.

(2)

Berechne das Integral von $\displaystyle\int_{0}^{k}(\mathrm e^{-x}-k)\;\mathrm dx$ in Abhängigkeit von $k.$

(2 + 4 Punkte)

Für jedes $r\in\mathbb{R}$ mit $r\neq-4$ bilden die Punkte $A(0\mid 0\mid -4),$ $B(3\mid 4\mid -4),$ $C,$ $D(-8\mid 6\mid -4),$ $E_r,$ $F_r,$ $G_r(-5\mid 10\mid r)$ und $H_r$ einen Quader. In der Abbildung 1 ist ein Quader für einen konkreten Wert von $r$ dargestellt.

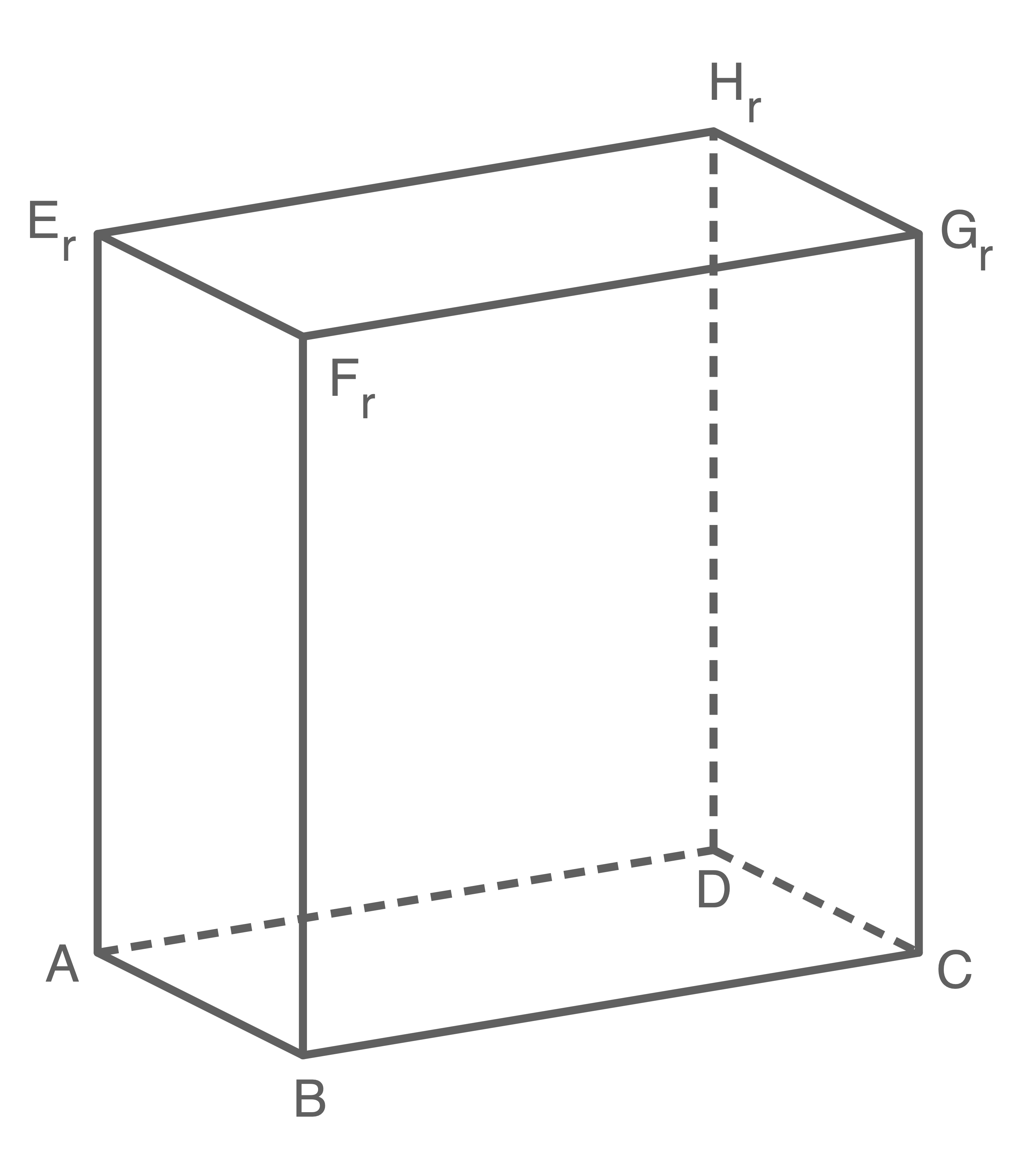
Abbildung 1

(1)

Weise rechnerisch nach, dass die Kanten $\overline{AB}$ und $\overline{AD}$ senkrecht zueinander verlaufen.

(2)

Bestimme die Werte von $r$ , für die die Raumdiagonale $\overline{AG_r}$ die Länge $15\,\text{LE}$ besitzt.

(2 + 4 Punkte)

Bei einem Stadtfest gibt es ein Glücksrad, welches in zehn gleich große Sektoren unterteilt ist (siehe Abbildung 2). Jede teilnehmende Person dreht das Glücksrad genau einmal.

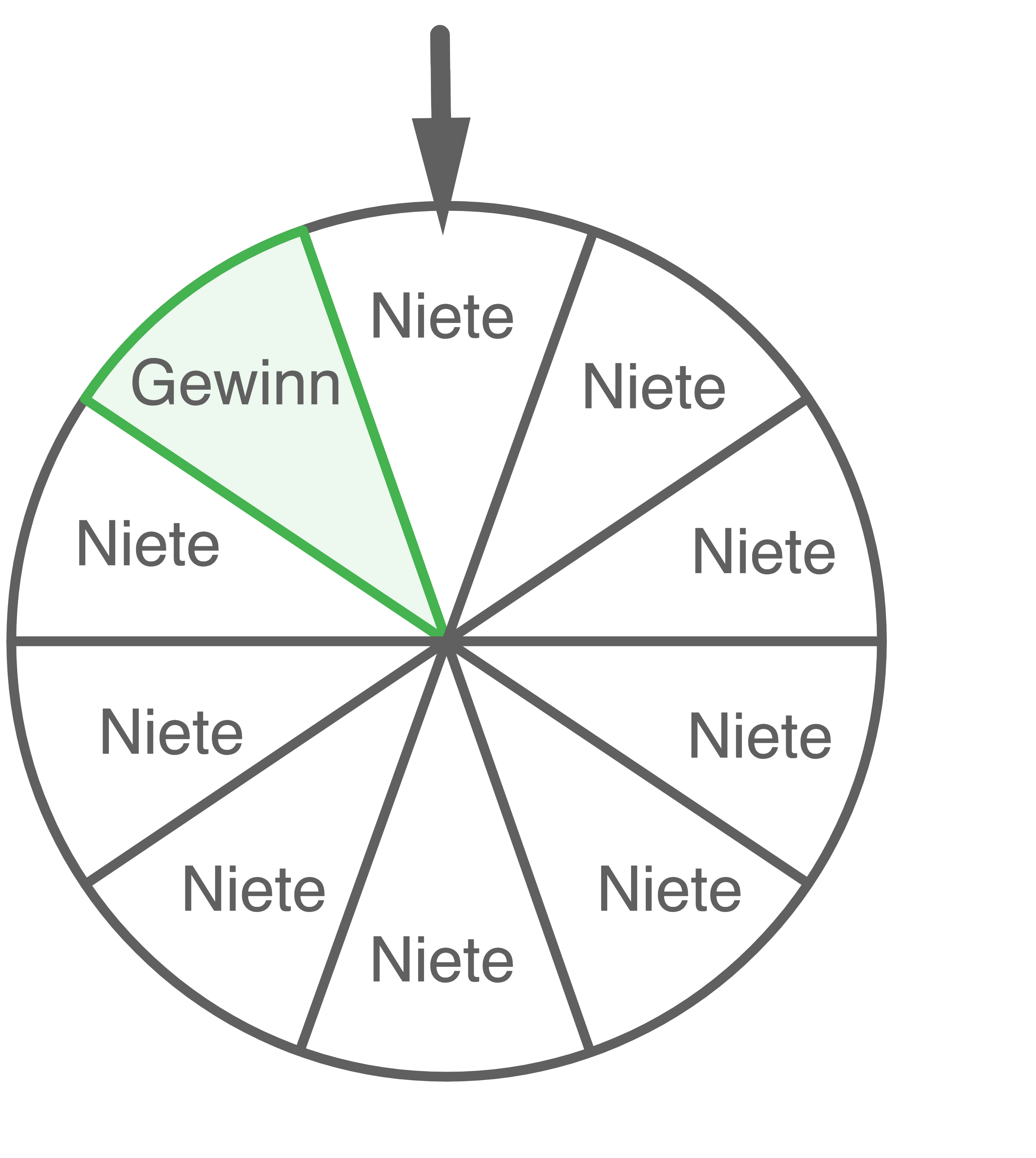
Abbildung 2

(1)

Beschreibe in diesem Sachzusammenhang ein Ereignis, dessen Wahrscheinlichkeit mit dem folgenden Term berechnet werden kann:

Vollständigen Term anzeigen

$\pmatrix{7\\0}\cdot 0,1^0 ...$

(2)

Gib einen Term an, mit dem die Wahrscheinlichkeit für das folgende Ereignis berechnet werden kann:
„Von 20 teilnehmenden Personen erhalten genau vier Personen einen Gewinn.“

Ein anderes Glücksrad ist in $n$ gleich große Sektoren aufgeteilt. Zwei Personen drehen dieses Glücksrad jeweils genau einmal. Die Zufallsgröße $X$ gibt die Anzahl der Personen an, die einen Gewinn erhalten.
Es gilt: $P(X=0)=9\cdot P(X=2).$

(3)

Ermittle eine mögliche Gesamtzahl $n$ der Sektoren auf dem Glücksrad sowie die zugehörige Anzahl der Sektoren mit einem Gewinn.

(2 + 1 + 3 Punkte)

(1)

Durch Ausmultiplizieren der Funktion ergibt sich: $f(x)=x^3-x$

Erste Ableitung bestimmen:

$\(f$

(2)

Allgemeine Tangentengleichung: $y_t=m \cdot x +b.$

$y$ -Achsenabschnitt $b$ mittels des Funktionswertes bestimmen:

$\begin{array}[t]{rll} f \left(-\dfrac{1}{2}\right)&=& \left(-\dfrac{1}{2}\right)^3-\dfrac{1}{2} & \\[5pt] &=& -\dfrac{1}{8} - \left(-\dfrac{1}{2}\right)& \\[5pt] &=& -\dfrac{1}{8} + \dfrac{1}{2} & \\[5pt] &=&\dfrac{3}{8} \end{array}$

Steigung $m$ ermitteln:

$\(m=f$

Durch Einsetzen der Koordinaten von $f$ an der Stelle $x=-\dfrac{1}{2}$ und $m$ folgt:

$\begin{array}[t]{rll} \dfrac{3}{8}&=&\left(-\dfrac{1}{4} \right) \cdot \left( -\dfrac{1}{2}\right) +b &\quad \scriptsize \mid\;-\dfrac{1}{8} \\[5pt] \dfrac{3}{8} -\dfrac{1}{8}&=&b & \\[5pt] \dfrac{1}{4}&=& b \end{array}$

Die Tangentengleichung entspricht somit $y_t=-\dfrac{1}{4} \cdot x+\dfrac{1}{4}.$

(1)

Es soll gelten: $f_k (x)=0.$

Durch Einsetzen von $x=-1$ in $f_k (x)$ folgt:

$\begin{array}[t]{rll} f_k (-1)&=& 0 & \\[5pt] \mathrm e^{-(-1)} -k &=&0 &\quad \scriptsize \; +k\\[5pt] \mathrm e&=&k \end{array}$

Für $k=\mathrm e$ ist folglich $x=1$ eine Nullstelle von $f_k.$

(2)

Rechenweg anzeigen

$\displaystyle\int_{0}^{k}(\mathrm e^{-x} -k)\;\mathrm dx = -\mathrm e^{-k}-k^2 +1$

(1)

Die Kanten $\overline{AB}$ und $\overline{AD}$ verlaufen senkrecht zueinander, wenn das Skalarprodukt ihrer Vektoren null ist.

$\begin{array}[t]{rll} \overrightarrow{AB}&=&\overrightarrow{OB} -\overrightarrow{OA} & \\[5pt] &=& \pmatrix{3\\4\\-4} - \pmatrix{0\\0\\-4}& \\[5pt] &=& \pmatrix{3\\4\\0}& \\[5pt] \end{array}$

$\begin{array}[t]{rll} \overrightarrow{AD}&=&\overrightarrow{OD} - \overrightarrow{OA} & \\[5pt] &=& \pmatrix{-8\\6\\-4} - \pmatrix{0\\0\\-4} & \\[5pt] &=&\pmatrix {-8\\6\\0} \end{array}$

$\begin{array}[t]{rll} \overrightarrow{AB} \circ \overrightarrow{AD}&=&\pmatrix{3\\4\\0}\circ \pmatrix {-8\\6\\0} &\\[5pt] &=& 3\cdot (-8)+4 \cdot 6 +0 &\\[5pt] &=& 0 \end{array}$

Die beiden Kanten stehen somit senkrecht zueinander.

(2)

$\begin{array}[t]{rll} \overrightarrow{AG_r}&=&\overrightarrow{OG_r}- \overrightarrow{OA}&\\[5pt] &=&\pmatrix{-5\\10\\r}- \pmatrix{0\\0\\-4} &\\[5pt] &=&\pmatrix{-5\\10\\r+4} \end{array}$

Es soll gelten: