Aufgabe 2

Für jede reelle Zahl $k \geq 0$ ist durch die Gleichung

$f_k(x) = x^3-3\cdot k^2\cdot x,$ $x\in \mathbb{R},$

eine Funktion $f_k$ gegeben.

(1)

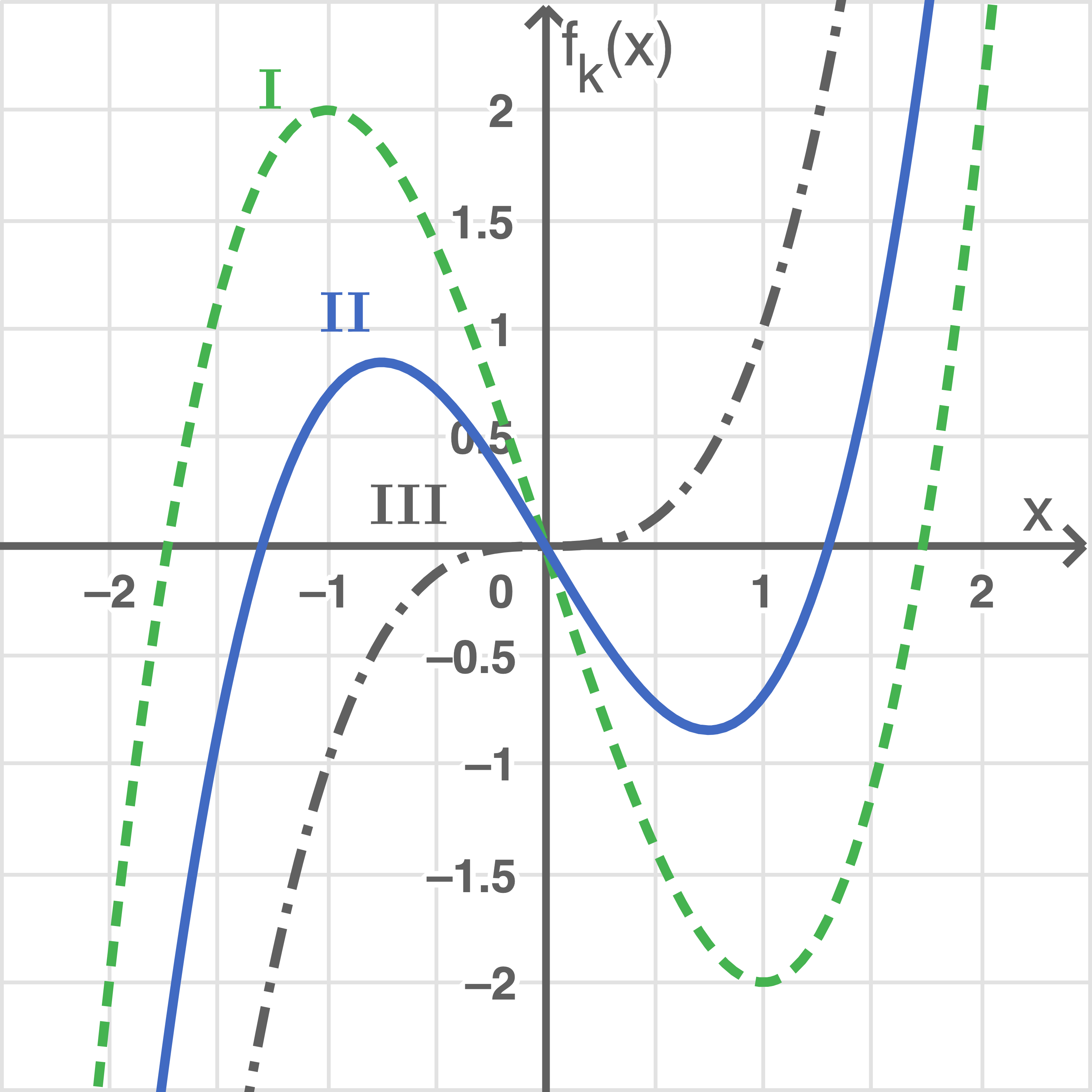
Die in der folgenden Abbildung 1 dargestellten Graphen $\text{I},$ $\text{II}$ und $\text{III}$ gehören jeweils zu einem der Werte $k = 0 ,$ $k = 0,75$ und $k = 1.$

Abbildung 1

Entscheide, welcher Wert zu welchem Graphen gehört.

(2)

Ermittle rechnerisch in Abhängigkeit von $k \geq 0$ die lokalen Extrempunkte des Graphen von $f_k$ und die Art der Extrempunkte (falls vorhanden).

(3 + 10 Punkte)

(1)

Bestimme rechnerisch den Inhalt $A$ der Fläche, die für $x \leq 0$ vom Graphen von $f_1$ und der $x$ -Achse eingeschlossen wird.

$\big[$ Zur Kontrolle: $A = 2,25\,\text{FE}. \big]$

Für jede reelle Zahl $a$ ist durch $g_a:\, y= a\cdot x$ eine Gerade $g_a$ durch den Ursprung des Koordinatensystems gegeben. Für $a \gt -3$ schneidet die zugehörige Gerade $g_a$ den Graphen von $f_1$ an den drei Stellen $x =-\sqrt{a+3} ,$ $x = 0$ und $x =\sqrt{a+3}.$

(2)

Für $a \gt -3$ wird zwischen der Geraden $g_a$ (unterer Rand) und dem Graphen von $f_1$ (oberer Rand) im Bereich $x \leq 0$ eine Fläche $F$ eingeschlossen.
Weise nach, dass für den Inhalt $I_a$ dieser Fläche $F$ gilt:

Gleichung anzeigen

$I_a=...$

[Hinweis: Die oben angegebenen Schnittstellen dürfen ohne Nachweis verwendet werden.]

(3)

Es gibt genau einen Wert $a \gt -3,$ für den die zugehörige Gerade $g_a$ die Fläche halbiert, die für $x \leq 0$ vom Graphen von $f_1$ und der $x$ -Achse eingeschlossen wird.
Bestimme diesen Wert auf zwei Nachkommastellen genau.

(7 + 4 + 3 Punkte)

Für jede reelle Zahl $k \geq 0$ ist durch $t_k:\, y = \left(0,75-3\cdot k^2 \right) \cdot x +0,25$ eine Tangente an den Graphen von $f_k$ im Punkt $P_k(-0,5\mid f_k(-0,5))$ gegeben.

[Nachweis nicht erforderlich.]

(1)

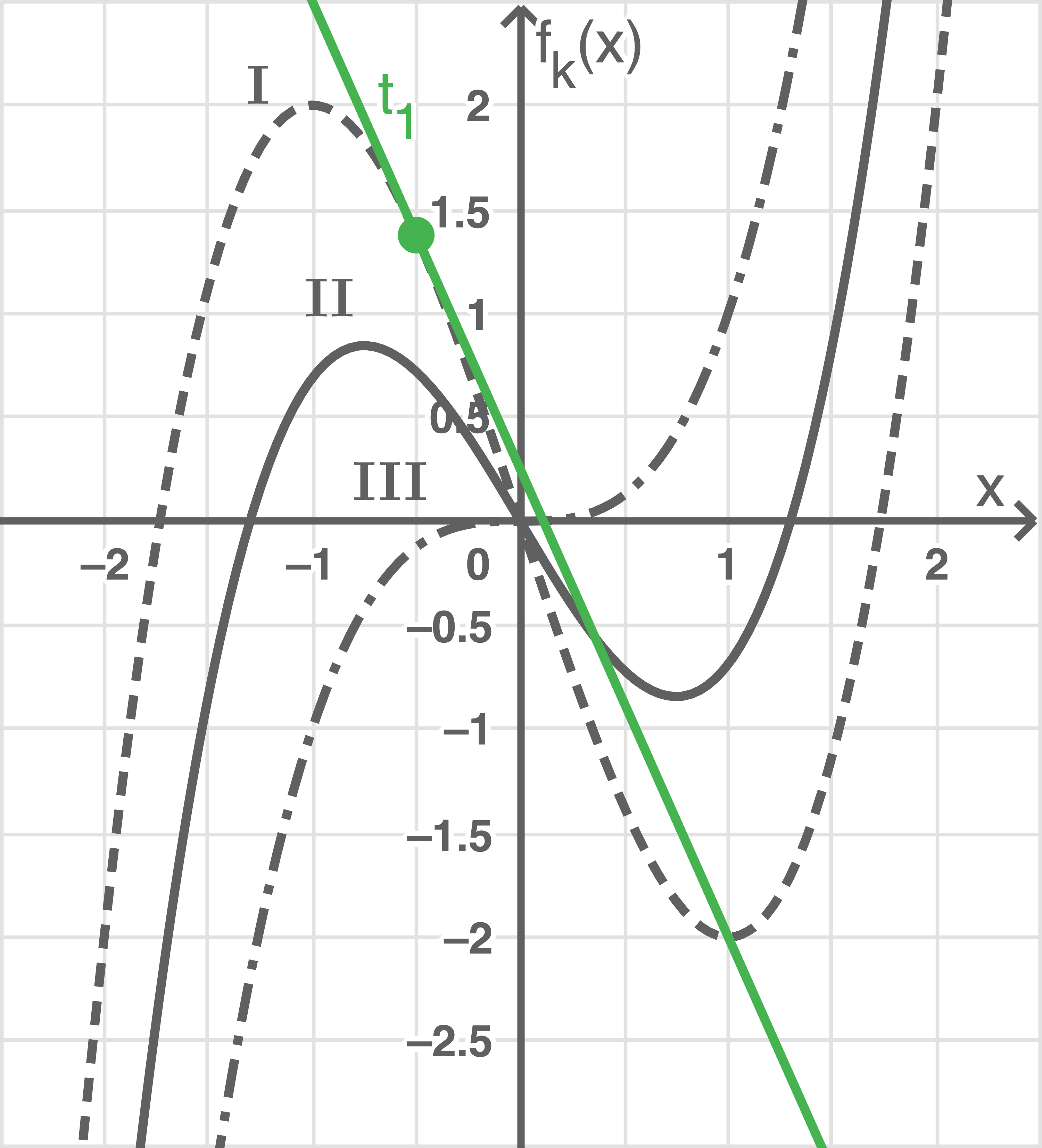
Zeichne die Tangente $t_1$ in die Abb. 2 ein.

(2)

Die Tangente $t_k$ und der Graph von $f_k$ schließen eine Fläche ein. Weise zunächst nach, dass die Differenzfunktion $d_k$ mit $d_k(x)= t_k(x) -f_k(x)$ nicht vom Parameter $k$ abhängt.

Bestimme den Inhalt der eingeschlossenen Fläche.

Abbildung 2

[Zur Kontrolle: Die gemeinsamen Punkte der Tangente $t_k$ und des Graphen von $f_k$ liegen bei $x =-0,5$ und $x = 1.$ ]

(3)

Zeige: Für jede reelle Zahl $r \gt 0$ ist die Gerade durch die Punkte $A_{r;k}(-r\mid f_k(-r))$ und $B_{r;k}(2\cdot r \mid f_k(2\cdot r))$ eine Tangente an den Graphen von $f_k$ an der Stelle $x=-r.$

(2 + 6 + 5 Punkte)

(1)

$k=0$ gehört zu Graph $\text{III}$

$k=0,75$ gehört zu Graph $\text{II}$

$k=1$ gehört zu Graph $\text{I}$

(2)

1. Schritt: Ableitungen bilden

$\(\begin{array}[t]{rll} f_k(x) &=& x^3-3k^2\cdot x \\[5pt] f_k$

2. Schritt: Notwendiges Kriterium für Extremstellen anwenden

$\(\begin{array}[t]{rll} f_k$

3. Schritt: Hinreichendes Kriterium für Extremstellen anwenden

$\(\begin{array}[t]{rll} f_k$

Für $k \gt 0$ ist $\(f_k$ und $\(f_k$ , also besitzt der Graph $f_k$ an der Stelle $x_1= -k$ einen lokalen Hochpunkt, an der Stelle $x_2=k$ einen lokalen Tiefpunkt.
Für $k=0$ ist $f_k(x)= x^3.$ Der Graph dieser Funktion besitzt keine lokalen Extrempunkte.

4. Schritt: $y$ -Koordinate berechnen

$\begin{array}[t]{rll} f_k(-k) &=& (-k)^3-3k^2\cdot (-k) \\[5pt] &=& 2k^3 \\[10pt] f_k(k) &=& k^3-3k^2\cdot k \\[5pt] &=& -2k^3 \\[5pt] \end{array}$

Für $k=0$ besitzt der Graph von $f_k$ keine lokalen Extrempunkte. Für $k\gt 0$ besitzt der Graph von $f_k$ den Hochpunkt $H(-k \mid 2k^3)$ und den Tiefpunkt $T(k\mid -2k^3).$

(1)

1. Schritt: Integrationsgrenzen bestimmen

Die Integrationsgrenzen entsprechen den Nullstellen von $f_1$ für $x\leq 0.$

$\begin{array}[t]{rll} f_1(x) &=& 0 \\[5pt] x^3-3\cdot 1^2 \cdot x &=& 0 \\[5pt] \end{array}$

Mit der graphischen Lösung des GTRs folgt $x_2=-\sqrt{3}$ und $x_3= \sqrt{3}.$

2. Schritt: Flächeninhalt berechnen

Rechenweg anzeigen

$A=2,25 \;\text{[FE]}$

(2)

Der Inhalt der Fläche zwischen den beiden Graphen $f_1$ und $g_a$ wird mit Hilfe eines Integrals berechnet:

Rechenweg anzeigen

$I_a=...$

(3)

Der Gesamtflächeninhalt der vom Graphen von $f_1$ und der $x$ -Achse für $x \leq 0$ eingeschlossenen Fläche wurde in b) (1) berechnet:

$A= 2,25$

Es ist also $a$ gesucht, sodass für den Flächeninhalt $I_a$ aus b) (2) gilt:

Rechenweg anzeigen

$...=1,125$

Diese Gleichung wird mit dem GTR gelöst:

$\blacktriangleright$ TI 84-PLUS

Bestimmt werden die Schnittpunkte des Graphen von $I(a)$ mit der Gerade $y = 1,125.$

2nd $\to$ trace (calc) $\to$ 5: intersect

$\blacktriangleright$ Casio fx-CG

Bestimmt wird der $x$ -Wert zum $y$ -Wert $1,125$ von $I(a)$ mit dem X-CAL-Befehl.

F5 (G-Solv) $\to$ F6 $\to$ F2: X-CAL

Es ergibt sich $a \approx -0,88.$

(1)

(2)

Unabhängigkeit des Parameters nachweisen

Rechenweg anzeigen

$d_k$ hängt also nicht vom Parameter $k$ ab.

Inhalt der eingeschlossenen Fläche bestimmen

1. Schritt: Integrationsgrenzen bestimmen

$\begin{array}[t]{rll} t_k(x) &=& f_k(x) &\quad \scriptsize \mid\; -f_k(x) \\[5pt] t_k(x) -f_k(x) &=& 0 \\[5pt] d_k(x) &=& 0 \\[5pt] -x^3 +0,75x +0,25 &=& 0 \end{array}$

Mit dem GTR folgt $x_1= -0,5$ und $x_2 = 1.$

2. Schritt: Flächeninhalt bestimmen

$\begin{array}[t]{rll} A_k &=& \displaystyle\int_{-0,5}^{1}\left( t_k(x) -f_k(x)\right)\;\mathrm dx \\[5pt] &=& \displaystyle\int_{-0,5}^{1}d_k(x)\;\mathrm dx \\[5pt] \end{array}$

Mit dem GTR folgt $A_k \approx 0,42.$

Der Inhalt der von den Graphen von $t_k$ und $f_k$ eingeschlossenen Fläche beträgt ca. $0,42\,\text{[FE]}.$

(3)

1. Schritt: Steigung der Gerade durch $A_{r;k}$ und $B_{r;k}$ bestimmen

Rechenweg anzeigen

$m_{A;B} =3r^2-3\cdot k^2$

2. Schritt: Steigung der Tangente an der Stelle $x=-r$ bestimmen

$\(\begin{array}[t]{rll} f_k$

Die Steigung der Geraden durch die Punkte $A_{r;k}$ und $B_{r;k}$ stimmt mit der Steigung der Tangente an den Graphen von $f_k$ an der Stelle $x=-r$ überein. Zudem verlaufen beide Geraden durch den Punkt $(-r\mid f_k(-r))$ und sind damit identisch. Die Gerade durch die Punkte $A_{r;k}$ und $B_{r;k}$ ist also eine Tangente an den Graphen von $f_k$ an der Stelle $x=-r.$