Aufgabe 6
Aufgabenstellung
Eine Firma stellt mit zwei verschiedenen Maschinen  und
und  Bodenfliesen aus Keramik her. Damit eine Fliese als „1. Wahl“ gilt, muss sie strenge Qualitätsnormen erfüllen. Alle anderen Fliesen werden als „2. Wahl“ bezeichnet. Eine Fliese, die mit Maschine
Bodenfliesen aus Keramik her. Damit eine Fliese als „1. Wahl“ gilt, muss sie strenge Qualitätsnormen erfüllen. Alle anderen Fliesen werden als „2. Wahl“ bezeichnet. Eine Fliese, die mit Maschine  produziert wurde, ist erfahrungsgemäß mit einer Wahrscheinlichkeit von 0,9 „1. Wahl“ (d. h. mit der Wahrscheinlichkeit von 0,1 „2. Wahl“). Maschine
produziert wurde, ist erfahrungsgemäß mit einer Wahrscheinlichkeit von 0,9 „1. Wahl“ (d. h. mit der Wahrscheinlichkeit von 0,1 „2. Wahl“). Maschine  produziert lediglich mit einer Wahrscheinlichkeit von 0,8 „1. Wahl“-Fliesen. Dabei kann für beide Maschinen davon ausgegangen werden, dass die Produktion von Fliesen 1. und 2. Wahl jeweils stochastisch unabhängig erfolgt. Fliesen, die von Maschine
produziert lediglich mit einer Wahrscheinlichkeit von 0,8 „1. Wahl“-Fliesen. Dabei kann für beide Maschinen davon ausgegangen werden, dass die Produktion von Fliesen 1. und 2. Wahl jeweils stochastisch unabhängig erfolgt. Fliesen, die von Maschine  produziert wurden, werden im Folgenden als
produziert wurden, werden im Folgenden als  -Fliesen bezeichnet, Fliesen von Maschine
-Fliesen bezeichnet, Fliesen von Maschine  als
als  -Fliesen. Jede Packung enthält 20 Fliesen, die von derselben Maschine stammen.
-Fliesen. Jede Packung enthält 20 Fliesen, die von derselben Maschine stammen.
 Die 20 Fliesen einer Packung
Die 20 Fliesen einer Packung  -Fliesen wurden in 4 Reihen mit jeweils 5 Fliesen verlegt.
-Fliesen wurden in 4 Reihen mit jeweils 5 Fliesen verlegt.
 - Regeln für Binomialverteilungen
- Regeln für Binomialverteilungen
Eine mit den Parametern und
und  binomialverteilte Zufallsgröße
binomialverteilte Zufallsgröße  hat den Erwartungswert
hat den Erwartungswert  und die Standardabweichung
und die Standardabweichung  .
.
Wenn die LAPLACE-Bedingung erfüllt ist, gelten die
erfüllt ist, gelten die  -Regeln:
-Regeln:
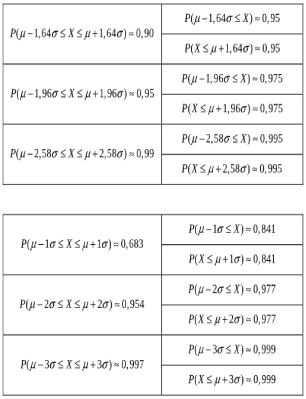 Tabelle 2: Kumulierte Binomialverteilung für n=10 und n=20
Tabelle 2: Kumulierte Binomialverteilung für n=10 und n=20

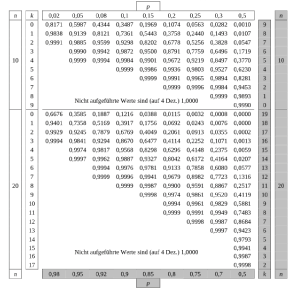 Bei grau unterlegtem Eingang, d.h.
Bei grau unterlegtem Eingang, d.h.  , gilt:
, gilt:  abgelesener Wert
Tabelle 3: Kumulierte Binomialverteilung für n=100
abgelesener Wert
Tabelle 3: Kumulierte Binomialverteilung für n=100

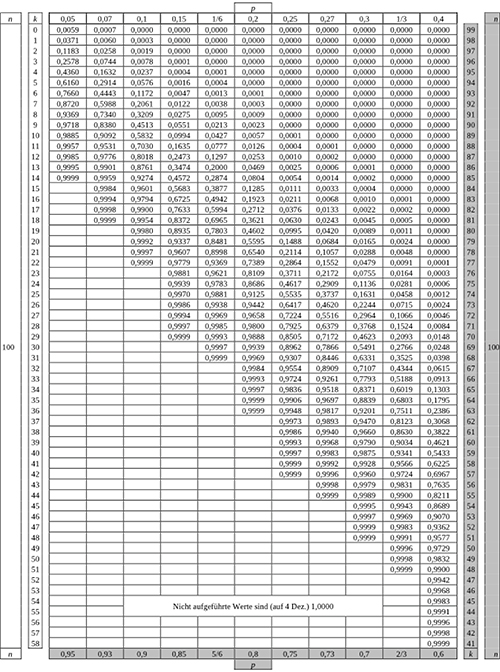 Bei grau unterlegtem Eingang, d.h.
Bei grau unterlegtem Eingang, d.h.  , gilt:
, gilt:  abgelesener Wert
Tabelle 4: Normalverteilung
abgelesener Wert
Tabelle 4: Normalverteilung


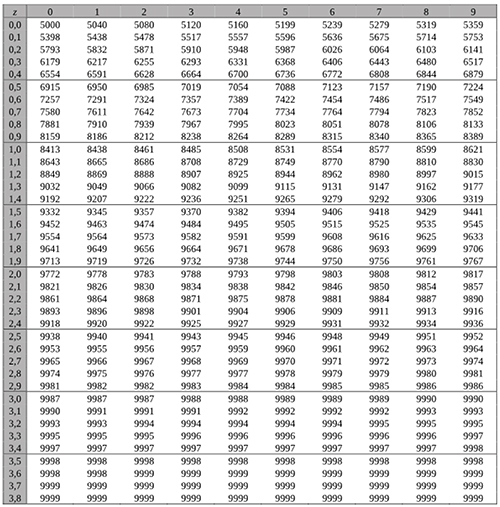 Beispiele für den Gebrauch:
Beispiele für den Gebrauch:



a) (1) Berechne die Wahrscheinlichkeit dafür, dass in einer Packung  -Fliesen genau zwei „2. Wahl“-Fliesen enthalten sind.
-Fliesen genau zwei „2. Wahl“-Fliesen enthalten sind.
(2P)
(2) Berechne die Wahrscheinlichkeit dafür, dass in einer Packung  -Fliesen maximal
-Fliesen maximal  % der Fliesen die Qualität „1. Wahl“ haben.
% der Fliesen die Qualität „1. Wahl“ haben.
(3P)
(3) Bestimme die Wahrscheinlichkeit  dafür, dass eine zufällig ausgewählte Reihe nur „1. Wahl“-Fliesen enthält. [Kontrollergebnis
dafür, dass eine zufällig ausgewählte Reihe nur „1. Wahl“-Fliesen enthält. [Kontrollergebnis  ]
]
(2P)
(4) Ermittle die Wahrscheinlichkeit dafür, dass es mindestens eine Reihe gibt, die nur „1. Wahl“-Fliesen enthält.
(4P)
b) An Großabnehmer verkauft die Firma auch Paletten, die jeweils 500 Packungen Fliesen von derselben Maschine enthalten. Ein Bauunternehmer bestellt eine Palette mit  -Fliesen. Da die Packungen bei der Lieferung nicht gekennzeichnet sind, befürchtet er, versehentlich eine Palette mit
-Fliesen. Da die Packungen bei der Lieferung nicht gekennzeichnet sind, befürchtet er, versehentlich eine Palette mit  -Fliesen erhalten zu haben.
-Fliesen erhalten zu haben.
Er beschließt, für einen Test der Lieferung zufällig 100 Fliesen zu entnehmen und die Anzahl der „2. Wahl“-Fliesen in dieser Stichprobe zu bestimmen.
der „2. Wahl“-Fliesen in dieser Stichprobe zu bestimmen.
Er beschließt, für einen Test der Lieferung zufällig 100 Fliesen zu entnehmen und die Anzahl
(1) Begründe, dass  als binomialverteilte Zufallsgröße aufgefasst werden kann, wobei die Trefferwahrscheinlichkeit bei
als binomialverteilte Zufallsgröße aufgefasst werden kann, wobei die Trefferwahrscheinlichkeit bei  -Fliesen
-Fliesen  und bei
und bei  -Fliesen
-Fliesen  beträgt.
beträgt.
(3P)
(2) Es wird ein Hypothesentest mit der Nullhypothese  durchgeführt.
durchgeführt.
Wird verworfen, wird die Palette angenommen, sonst wird sie zurückgeschickt.
verworfen, wird die Palette angenommen, sonst wird sie zurückgeschickt.
Erkläre die Wahl der Nullhypothese.
Wird
Erkläre die Wahl der Nullhypothese.
(4P)
(3) Ermittle eine Entscheidungsregel (auf Basis der genannten Nullhypothese) für die oben genannte Stichprobe von 100 Fliesen mit einer Irrtumswahrscheinlichkeit (d. h. Wahrscheinlichkeit für einen Fehler 1. Art) von höchstens  %.
%.
[Zur Kontrolle: wird für
wird für  angelehnt.]
angelehnt.]
[Zur Kontrolle:
(5P)
(4) Berechne die Wahrscheinlichkeit  , dass die Hypothese
, dass die Hypothese  aufgrund der Entscheidungsregel aus (3) irrtümlich nicht abgelehnt wird, obwohl die Palette tatsächlich
aufgrund der Entscheidungsregel aus (3) irrtümlich nicht abgelehnt wird, obwohl die Palette tatsächlich  -Fliesen enthält, also
-Fliesen enthält, also  gilt.
gilt.
Berechne die Wahrscheinlichkeit , dass die Hypothese
, dass die Hypothese  irrtümlich abgelehnt wird, obwohl die Palette tatsächlich
irrtümlich abgelehnt wird, obwohl die Palette tatsächlich  -Fliesen enthält, also
-Fliesen enthält, also  gilt.
gilt.
[Zur Kontrolle: ,
,  ]
]
Berechne die Wahrscheinlichkeit
[Zur Kontrolle:
(6P)
(5) Im Lager des Herstellers befanden sich 7 Paletten mit  -Fliesen und 3 Paletten mit
-Fliesen und 3 Paletten mit  -Fliesen, aus denen die angelieferte Palette zufällig ausgewählt wurde.
-Fliesen, aus denen die angelieferte Palette zufällig ausgewählt wurde.
Bestimme mit Hilfe der Wahrscheinlichkeiten und
und  die gesamte Irrtumswahrscheinlichkeit für den Test.
die gesamte Irrtumswahrscheinlichkeit für den Test.
Bestimme mit Hilfe der Wahrscheinlichkeiten
(4P)
c) Für besonders anspruchsvolle Kunden soll eine Sorte „Premium“ angeboten werden, die nur aus „1. Wahl“-Fliesen besteht. Dazu will die Firma die „2. Wahl“-Fliesen aus der Produktion der Maschine  aussortieren. Für einen ersten Sortiervorgang wird ein Testgerät verwendet, das allerdings nicht immer optimal funktioniert:
aussortieren. Für einen ersten Sortiervorgang wird ein Testgerät verwendet, das allerdings nicht immer optimal funktioniert:
Das Testgerät erkennt eine „2. Wahl“-Fliese mit einer Wahrscheinlichkeit von („Aussortierwahrscheinlichkeit“) und sortiert sie aus. Andererseits wird eine „1. Wahl“- Fliese mit einer Wahrscheinlichkeit von
(„Aussortierwahrscheinlichkeit“) und sortiert sie aus. Andererseits wird eine „1. Wahl“- Fliese mit einer Wahrscheinlichkeit von  zu Unrecht als „2. Wahl“ aussortiert.
zu Unrecht als „2. Wahl“ aussortiert.
Das Testgerät erkennt eine „2. Wahl“-Fliese mit einer Wahrscheinlichkeit von
(1) Stelle die Situation graphisch dar (mit einer Vierfeldertafel oder einem Baumdiagramm mit allen Pfadwahrscheinlichkeiten).
Gib die Wahrscheinlichkeit an, mit der das Testgerät eine zufällig ausgewählte Fliese als „1. Wahl“ einstuft (also nicht aussortiert).
Gib die Wahrscheinlichkeit an, mit der das Testgerät eine zufällig ausgewählte Fliese als „1. Wahl“ einstuft (also nicht aussortiert).
(7P)
(2) Bestimme die Wahrscheinlichkeit dafür, dass eine Fliese, die bei der Prüfung nicht aussortiert wurde, in Wirklichkeit eine „2. Wahl“-Fliese ist.
(4P)
(3) Bestimme, wie groß die „Aussortierwahrscheinlichkeit“  des Testgeräts mindestens sein muss, damit die Wahrscheinlichkeit aus (2) (und damit der erwartete Anteil der „2. Wahl“-Fliesen nach dem Aussortieren) durch die Prüfung auf unter
des Testgeräts mindestens sein muss, damit die Wahrscheinlichkeit aus (2) (und damit der erwartete Anteil der „2. Wahl“-Fliesen nach dem Aussortieren) durch die Prüfung auf unter  % gesenkt wird.
% gesenkt wird.
(6P)
Tabelle 1: Eine mit den Parametern
Wenn die LAPLACE-Bedingung




a)(1)
 Bestimmen der Wahrscheinlichkeit
Du sollst die Wahrscheinlichkeit dafür berechnen, dass in einer Packung A-Fliesen, die aus 20 Fliesen von Maschine A besteht, genau zwei „2.Wahl“-Fliesen enthalten sind.
Betrachte dazu die Zufallsvariable
Bestimmen der Wahrscheinlichkeit
Du sollst die Wahrscheinlichkeit dafür berechnen, dass in einer Packung A-Fliesen, die aus 20 Fliesen von Maschine A besteht, genau zwei „2.Wahl“-Fliesen enthalten sind.
Betrachte dazu die Zufallsvariable  , die die Anzahl der „2. Wahl“-Fliesen in einer zufällig ausgewählten Packung von A-Fliesen beschreibt. Gesucht ist nun die Wahrscheinlichkeit
, die die Anzahl der „2. Wahl“-Fliesen in einer zufällig ausgewählten Packung von A-Fliesen beschreibt. Gesucht ist nun die Wahrscheinlichkeit
 Da in der Aufgabenstellung angegeben ist, dass die Produktion stochastisch unabhängig ist und man davon ausgehen kann, dass jede Fliese von Maschine A die gleiche Wahrscheinlichkeit besitzt „2. Wahl“ oder „1. Wahl“ zu sein, kannst du davon ausgehen, dass
Da in der Aufgabenstellung angegeben ist, dass die Produktion stochastisch unabhängig ist und man davon ausgehen kann, dass jede Fliese von Maschine A die gleiche Wahrscheinlichkeit besitzt „2. Wahl“ oder „1. Wahl“ zu sein, kannst du davon ausgehen, dass  binomialverteilt ist. Die Parameter lauten hier
binomialverteilt ist. Die Parameter lauten hier  und
und  . Die gesuchte Wahrscheinlichkeit kannst du dann entweder mit der Formel für die Binomialverteilung oder deinem GTR berechnen.
. Die gesuchte Wahrscheinlichkeit kannst du dann entweder mit der Formel für die Binomialverteilung oder deinem GTR berechnen.
 Lösungsweg A: GTR
Du kannst den binompdf-Befehl deines GTR verwenden. Diesen findest du unter
Lösungsweg A: GTR
Du kannst den binompdf-Befehl deines GTR verwenden. Diesen findest du unter
 ,
,  und
und  eingeben. Du erhältst dann das Ergebnis
eingeben. Du erhältst dann das Ergebnis  .
.
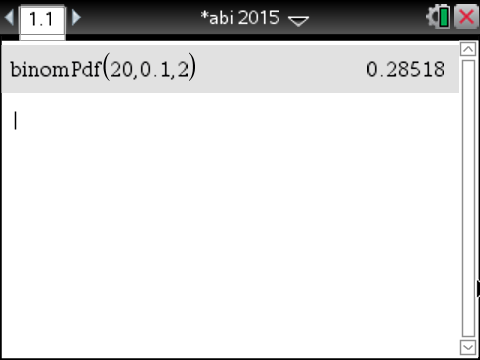 Mit einer Wahrscheinlichkeit von
Mit einer Wahrscheinlichkeit von  sind in einer Packung A-Fliesen genau 2 „2. Wahl“-Fliesen enthalten.
sind in einer Packung A-Fliesen genau 2 „2. Wahl“-Fliesen enthalten.
 Lösungsweg B: Handschriftlich
Für eine binomialverteilte Zufallsvariable
Lösungsweg B: Handschriftlich
Für eine binomialverteilte Zufallsvariable  mit den Parametern
mit den Parametern  und
und  gilt:
gilt:
 Setze dort nun die entsprechenden Werte ein und erhalte so folgendes:
Setze dort nun die entsprechenden Werte ein und erhalte so folgendes:
![\(\begin{array}[t]{rll}
P(X=2)&=&\binom{20}{2}\cdot 0,1^2\cdot (1-0,1)^{20-2} &\quad \scriptsize \\[5pt]
&=& \binom{20}{2}\cdot 0,1^2\cdot 0,9^{18}&\quad \scriptsize \\[5pt]
&\approx&0,2852 &\quad \scriptsize \\[5pt]
&=&28,52\,\% &\quad \scriptsize \\
\end{array}\)](https://mathjax.schullv.de/73070678ba03add762b08f9a785429df264a0e67b8ea22f133646fb1b1598c03?color=5a5a5a) Mit einer Wahrscheinlichkeit von
Mit einer Wahrscheinlichkeit von  sind in einer Packung A-Fliesen genau 2 „2. Wahl“-Fliesen enthalten.
sind in einer Packung A-Fliesen genau 2 „2. Wahl“-Fliesen enthalten.
6: Statistik  5: Verteilungen
5: Verteilungen  D: Binomial Pdf
D: Binomial Pdf
Du musst dann die entsprechenden Parameter 
a) (2)
 Wahrscheinlichkeit bestimmen
Nun sollst du die Wahrscheinlichkeit dafür berechnen, dass in einer Packung A-Fliesen maximal
Wahrscheinlichkeit bestimmen
Nun sollst du die Wahrscheinlichkeit dafür berechnen, dass in einer Packung A-Fliesen maximal  der Fliesen „1.Wahl“-Fliesen sind. Berechne dazu zunächst wie viele Fliesen es demnach höchstens sein dürfen um die
der Fliesen „1.Wahl“-Fliesen sind. Berechne dazu zunächst wie viele Fliesen es demnach höchstens sein dürfen um die  -Grenze nicht zu überschreiten und forme diese Aussage in eine Aussage über die „2. Wahl“-Fliesen um. Betrachtest du dann wieder die Zufallsvariable
-Grenze nicht zu überschreiten und forme diese Aussage in eine Aussage über die „2. Wahl“-Fliesen um. Betrachtest du dann wieder die Zufallsvariable  , so hat die gesuchte Wahrscheinlichkeit die Form
, so hat die gesuchte Wahrscheinlichkeit die Form  . Du kannst nun die kumulierte Binomialverteilung verwenden.
1. Schritt: Maximale Anzahl an „1. Wahl“-Fliesen berechnen
Maximal
. Du kannst nun die kumulierte Binomialverteilung verwenden.
1. Schritt: Maximale Anzahl an „1. Wahl“-Fliesen berechnen
Maximal  der Fliesen sollen „1. Wahl“-Fliesen sein:
der Fliesen sollen „1. Wahl“-Fliesen sein:
 Es sollen maximal
Es sollen maximal  Fliesen aus der Packung mit 20 Fliesen „1. Wahl“-Fliesen sein. Dies ist genau dann der Fall, wenn sich mindestens
Fliesen aus der Packung mit 20 Fliesen „1. Wahl“-Fliesen sein. Dies ist genau dann der Fall, wenn sich mindestens  „2. Wahl“-Fliesen in der Packung befinden. Gesucht ist also die Wahrscheinlichkeit
„2. Wahl“-Fliesen in der Packung befinden. Gesucht ist also die Wahrscheinlichkeit  .
2. Schritt: Wahrscheinlichkeit berechnen
Bringe die gesuchte Wahrscheinlichkeit zunächst mit Hilfe des Gegenereignisses in eine Form der Art
.
2. Schritt: Wahrscheinlichkeit berechnen
Bringe die gesuchte Wahrscheinlichkeit zunächst mit Hilfe des Gegenereignisses in eine Form der Art  , damit du die Tabelle zur kumulierten Binomialverteilung oder den binomcdf-Befehl deines GTR verwenden kannst:
, damit du die Tabelle zur kumulierten Binomialverteilung oder den binomcdf-Befehl deines GTR verwenden kannst:

 Lösungsweg A: GTR
Den binomcdf-Befehl deines GTR findest du unter
Lösungsweg A: GTR
Den binomcdf-Befehl deines GTR findest du unter
 Mit einer Wahrscheinlichkeit von ca.
Mit einer Wahrscheinlichkeit von ca.  befinden sich in einer Packung A-Fliesen höchstens
befinden sich in einer Packung A-Fliesen höchstens  „1. Wahl“-Fliesen.
„1. Wahl“-Fliesen.
 Lösungsweg B: Tabelle
Lies aus der Tabelle zur kummulierten Binomialverteilung für
Lösungsweg B: Tabelle
Lies aus der Tabelle zur kummulierten Binomialverteilung für  den Wert aus der Spalte für
den Wert aus der Spalte für  und der Zeile für
und der Zeile für  ab. So erhältst du folgendes Ergebnis:
ab. So erhältst du folgendes Ergebnis:
 .
Mit einer Wahrscheinlichkeit von ca.
.
Mit einer Wahrscheinlichkeit von ca.  befinden sich in einer Packung A-Fliesen höchstens
befinden sich in einer Packung A-Fliesen höchstens  „1. Wahl“-Fliesen.
„1. Wahl“-Fliesen.
6: Statistik  5: Verteilungen
5: Verteilungen  E: Binomial Cdf
E: Binomial Cdf
Dort musst du nun wie oben die entsprechenden Parameter eingeben und erhältst dann das folgende Ergebnis
a) (3)
 Wahrscheinlichkeit berechnen
Du sollst die Wahrscheinlichkeit dafür berechnen, dass alle Fliesen in einer zufällig ausgewählten Reihe, die aus
Wahrscheinlichkeit berechnen
Du sollst die Wahrscheinlichkeit dafür berechnen, dass alle Fliesen in einer zufällig ausgewählten Reihe, die aus  Fliesen besteht, „1. Wahl“-Fliesen sind. Betrachte dazu die Zufallsvariable
Fliesen besteht, „1. Wahl“-Fliesen sind. Betrachte dazu die Zufallsvariable  , die die Anzahl der „1. Wahl“-Fliesen in einer Reihe beschreibt. Diese ist aus den gleichen Gründen wie
, die die Anzahl der „1. Wahl“-Fliesen in einer Reihe beschreibt. Diese ist aus den gleichen Gründen wie  binomialverteilt, allerdings mit den Parametern
binomialverteilt, allerdings mit den Parametern  und
und  .
.
Gesucht ist dann die Wahrscheinlichkeit . Diese lässt sich wieder mit der Formel für die Binomialverteilung oder dem Binompdf-Befehl deines GTR berechnen. In beiden Fällen erhältst du folgendes Ergebnis:
. Diese lässt sich wieder mit der Formel für die Binomialverteilung oder dem Binompdf-Befehl deines GTR berechnen. In beiden Fällen erhältst du folgendes Ergebnis:
![\(\begin{array}[t]{rll}
P(Y=5)&=&\binom{5}{5}\cdot 0,8^5\cdot 0,2^0 &\quad \scriptsize \\[5pt]
&=& 0,8 ^5 &\quad \scriptsize \\[5pt]
&\approx& 0,32768 &\quad \scriptsize \\[5pt]
&=& 32,768\,\% &\quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/c104175ef9d434ca20e764ca6702dc4ab35ceab81f3444760120267cf905ecfa?color=5a5a5a) Mit einer Wahrscheinlichkeit von ca.
Mit einer Wahrscheinlichkeit von ca.  besteht eine zufällig ausgewählte Reihe nur aus „1. Wahl“-Fliesen .
besteht eine zufällig ausgewählte Reihe nur aus „1. Wahl“-Fliesen .
Gesucht ist dann die Wahrscheinlichkeit
a) (4)
 Wahrscheinlichkeit berechnen
Hier sollst du nun die Wahrscheinlichkeit dafür berechnen, dass es unter den
Wahrscheinlichkeit berechnen
Hier sollst du nun die Wahrscheinlichkeit dafür berechnen, dass es unter den  Reihen mindestens eine gibt, die nur „1. Wahl“-Fliesen enthält. Betrachte dazu die Zufallsvariable
Reihen mindestens eine gibt, die nur „1. Wahl“-Fliesen enthält. Betrachte dazu die Zufallsvariable  , die die zufällige Anzahl der Reihen beschreibt, die nur aus „1. Wahl“-Fliesen bestehen. Dann ist
, die die zufällige Anzahl der Reihen beschreibt, die nur aus „1. Wahl“-Fliesen bestehen. Dann ist  binomialverteilt mit den Parametern
binomialverteilt mit den Parametern  und
und  , da jede Reihe die gleiche Wahrscheinlichkeit besitzt nur aus „1. Wahl“-Fliesen zu bestehen und die Besetzung einer Reihe nicht von der Besetzung der übrigen Reihen abhängt.
Gesucht ist demnach nun die Wahrscheinlichkeit
, da jede Reihe die gleiche Wahrscheinlichkeit besitzt nur aus „1. Wahl“-Fliesen zu bestehen und die Besetzung einer Reihe nicht von der Besetzung der übrigen Reihen abhängt.
Gesucht ist demnach nun die Wahrscheinlichkeit  , welche du wieder wie oben berechnen kannst:
, welche du wieder wie oben berechnen kannst:
![\(\begin{array}[t]{rll}
P(R \geq 1)&=&1- P(R \leq 0) &\quad \scriptsize\\[5pt]
&=& 1-P(R =0)&\quad \scriptsize \\[5pt]
&=&1- \binom{4}{0}\cdot 0, 32768^0\cdot (1-0, 32768)^4 &\quad \scriptsize \\[5pt]
&\approx&0,7957 &\quad \scriptsize \\[5pt]
&=&79,57\,\% &\quad \scriptsize \\
\end{array}\)](https://mathjax.schullv.de/90b49f4577ba2528557f12728bd1f01116ea7d6bef18dcc5350026e23e647d64?color=5a5a5a) Mit einer Wahrscheinlichkeit von ca.
Mit einer Wahrscheinlichkeit von ca.  gibt es unter den
gibt es unter den  Reihen mindestens eine Reihe, die nur aus „1. Wahl“-Fliesen besteht.
Reihen mindestens eine Reihe, die nur aus „1. Wahl“-Fliesen besteht.
b) (1)
 Binomialverteilung begründen
In diesem Aufgabenteil wird die Zufallsvariable
Binomialverteilung begründen
In diesem Aufgabenteil wird die Zufallsvariable  betrachtet, die die zufällige Anzahl der „2. Wahl“-Fliesen in einer Stichprobe mit
betrachtet, die die zufällige Anzahl der „2. Wahl“-Fliesen in einer Stichprobe mit  Fliesen aus einer Palette beschreibt. Du sollst nun begründen, warum
Fliesen aus einer Palette beschreibt. Du sollst nun begründen, warum  als binomialverteilt angenommen werden kann und erklären, dass dann entweder
als binomialverteilt angenommen werden kann und erklären, dass dann entweder  oder
oder  gilt.
Für eine binomialverteilte Zufallsgröße, müssen folgende Eigenschaften erfüllt sein:
gilt.
Für eine binomialverteilte Zufallsgröße, müssen folgende Eigenschaften erfüllt sein:
 erfüllt sind und betrachte anschließend den Parameter
erfüllt sind und betrachte anschließend den Parameter  .
Im vorliegenden Fall, besteht ein einzelnes Zufallsexperiment darin eine zufällig ausgewählte Fliese zu betrachten und den „1. Wahl“-Fliesen oder den „2. Wahl“-Fliesen zuzuordnen. Es gibt also auch nur diese beiden Möglichkeiten, eine Fliese muss entweder „1. Wahl“ oder „2. Wahl“ sein und kann nicht nichts von beidem oder beides sein. Man kann dabei „1. Wahl“-Fliesen als „Misserfolg“ und „2. Wahl“-Fliesen als „Erfolg“ bezeichnen. Damit ist die dritte Eigenschaft erfüllt.
Die erste Eigenschaft ist auch erfüllt, dies kannst du dem Einleitungstext der Aufgabe entnehmen. Danach ist die Produktion einer Fliese stochastisch unabhängig von der Produktion der anderen Fliesen.
Eine Palette enthält immer entweder nur A-Fliesen oder nur B-Fliesen, da eine Palette immer aus Fliesen von derselben Maschine besteht. Demnach hat auch jede Fliese aus einer Palette die gleiche Wahrscheinlichkeit eine „1. Wahl“-Fliese oder eine „2. Wahl“-Fliese zu sein. In dem Fall, dass die Fliesen der Palette aus Maschine A stammen, beträgt die Wahrscheinlichkeit dafür, dass eine Fliese „2. Wahl“ ist,
.
Im vorliegenden Fall, besteht ein einzelnes Zufallsexperiment darin eine zufällig ausgewählte Fliese zu betrachten und den „1. Wahl“-Fliesen oder den „2. Wahl“-Fliesen zuzuordnen. Es gibt also auch nur diese beiden Möglichkeiten, eine Fliese muss entweder „1. Wahl“ oder „2. Wahl“ sein und kann nicht nichts von beidem oder beides sein. Man kann dabei „1. Wahl“-Fliesen als „Misserfolg“ und „2. Wahl“-Fliesen als „Erfolg“ bezeichnen. Damit ist die dritte Eigenschaft erfüllt.
Die erste Eigenschaft ist auch erfüllt, dies kannst du dem Einleitungstext der Aufgabe entnehmen. Danach ist die Produktion einer Fliese stochastisch unabhängig von der Produktion der anderen Fliesen.
Eine Palette enthält immer entweder nur A-Fliesen oder nur B-Fliesen, da eine Palette immer aus Fliesen von derselben Maschine besteht. Demnach hat auch jede Fliese aus einer Palette die gleiche Wahrscheinlichkeit eine „1. Wahl“-Fliese oder eine „2. Wahl“-Fliese zu sein. In dem Fall, dass die Fliesen der Palette aus Maschine A stammen, beträgt die Wahrscheinlichkeit dafür, dass eine Fliese „2. Wahl“ ist,  und bei Fliesen aus Maschine B beträgt diese Wahrscheinlichkeit
und bei Fliesen aus Maschine B beträgt diese Wahrscheinlichkeit  . Somit hast du sowohl die zweite Eigenschaft begründet, als auch die Trefferwahrscheinlichkeit erklärt.
. Somit hast du sowohl die zweite Eigenschaft begründet, als auch die Trefferwahrscheinlichkeit erklärt.
- Die
einzelnen Zufallsexperimente sind unabhängig voneinander
- Die Wahrscheinlichkeit
für einen Erfolg ist in jedem einzelnen Zufallsexperiment gleich
- In den einzelnen Zufallsexperimenten gibt es nur zwei mögliche Ergebnisse
b) (2)
 Wahl der Nullhypothese erklären
In dem Hypothesentest wird die Nullhypothese wie folgt gewählt:
Wahl der Nullhypothese erklären
In dem Hypothesentest wird die Nullhypothese wie folgt gewählt:
 Du sollst diese Wahl nun erklären. Überlege dir dazu zunächst für welche Werte diese Hypothese abgelehnt wird und welche Folgen die Bestätigung bzw. die Ablehnung der Nullhypothese für den Bauunternehmer hätte.
Die Nullhypothese wird nur für signifikant zu kleine Werte abgelehnt, also dann wenn in der Stichprobe signifikant wenige „2. Wahl“-Fliesen gefunden werden. In einem solchen Fall kann der Bauunternehmer davon ausgehen, dass die Wahrscheinlichkeit für eine Fliese 2. Wahl kleiner als
Du sollst diese Wahl nun erklären. Überlege dir dazu zunächst für welche Werte diese Hypothese abgelehnt wird und welche Folgen die Bestätigung bzw. die Ablehnung der Nullhypothese für den Bauunternehmer hätte.
Die Nullhypothese wird nur für signifikant zu kleine Werte abgelehnt, also dann wenn in der Stichprobe signifikant wenige „2. Wahl“-Fliesen gefunden werden. In einem solchen Fall kann der Bauunternehmer davon ausgehen, dass die Wahrscheinlichkeit für eine Fliese 2. Wahl kleiner als  ist und es sich nicht um eine Palette aus der Herstellung von Maschine B handelt. Dann nimmt der Bauunternehmer die Palette an.
ist und es sich nicht um eine Palette aus der Herstellung von Maschine B handelt. Dann nimmt der Bauunternehmer die Palette an.
Der Bauunternehmer möchte also sicher gehen und nur solche Paletten annehmen, bei denen der Anteil der „2. Wahl“-Fliesen signifikant kleiner als ist. In jedem anderen Fall schickt er die Palette zurück. Damit soll möglichst ausgeschlossen werden, dass fälschlicherweise eine Palette mit B-Fliesen angenommen wird.
ist. In jedem anderen Fall schickt er die Palette zurück. Damit soll möglichst ausgeschlossen werden, dass fälschlicherweise eine Palette mit B-Fliesen angenommen wird.
Der Bauunternehmer möchte also sicher gehen und nur solche Paletten annehmen, bei denen der Anteil der „2. Wahl“-Fliesen signifikant kleiner als
b) (3)
 Entscheidungsregel formulieren
In dieser Aufgabe sollst du nun eine Entscheidungsregel für den beschriebenen Hypothesentest auf Grundlage der Irrtumswahrscheinlichkeit von
Entscheidungsregel formulieren
In dieser Aufgabe sollst du nun eine Entscheidungsregel für den beschriebenen Hypothesentest auf Grundlage der Irrtumswahrscheinlichkeit von  formulieren. Gesucht ist also die größte Anzahl
formulieren. Gesucht ist also die größte Anzahl  von Fliesen zweiter Wahl, für die die Nullhypothese gerade noch verworfen wird.
Betrachte hier die in der Aufgabenstellung eingeführte Zufallsvariable
von Fliesen zweiter Wahl, für die die Nullhypothese gerade noch verworfen wird.
Betrachte hier die in der Aufgabenstellung eingeführte Zufallsvariable  , die nach b) (1) binomialverteilt ist mit den Parametern
, die nach b) (1) binomialverteilt ist mit den Parametern  und
und  .
.
Die Irrtumswahrscheinlichkeit gibt an, dass die Wahrscheinlichkeit dafür, die Nullhypothese fälschlicherweise zu verwerfen höchstens betragen soll. Daraus ergibt sich folgende Ungleichung, aus der du den Wert
betragen soll. Daraus ergibt sich folgende Ungleichung, aus der du den Wert  berechnen kannst, für den die Nullhypothese gerade noch verworfen werden soll:
berechnen kannst, für den die Nullhypothese gerade noch verworfen werden soll:
 für alle
für alle  Da im vorliegenden Fall nur
Da im vorliegenden Fall nur  oder
oder  gelten kann, kannst du die Ungleichung unter der Annahme betrachten, dass laut Nullhypothese
gelten kann, kannst du die Ungleichung unter der Annahme betrachten, dass laut Nullhypothese  gilt. Du erhältst dann einen Wert für
gilt. Du erhältst dann einen Wert für  , indem du die Tabelle zur kumulierten Binomialverteilung „rückwärts“ anwendest. Suche in der Tabelle zu
, indem du die Tabelle zur kumulierten Binomialverteilung „rückwärts“ anwendest. Suche in der Tabelle zu  in der Spalte zu
in der Spalte zu  nach dem größten
nach dem größten  , bei dem der Tabelleneintrag gerade noch
, bei dem der Tabelleneintrag gerade noch  0,05 ist. Dann findest du folgendes:
0,05 ist. Dann findest du folgendes:
 .
Die Entscheidungsregel lautet demach wie folgt:
Werden in der Stichprobe von
.
Die Entscheidungsregel lautet demach wie folgt:
Werden in der Stichprobe von  Fliesen höchstens
Fliesen höchstens  Fliesen 2. Wahl gefunden , wird die Nullhypothese auf Grundlage der Irrtumswahrscheinlichkeit von
Fliesen 2. Wahl gefunden , wird die Nullhypothese auf Grundlage der Irrtumswahrscheinlichkeit von  verworfen und der Bauunternehmer schickt die Palette nicht zurück. Werden mehr als
verworfen und der Bauunternehmer schickt die Palette nicht zurück. Werden mehr als  Fliesen 2. Wahl gefunden, kann die Nullhypothese nicht verworfen werden und der Bauunternehmer schickt die Palette zurück.
Fliesen 2. Wahl gefunden, kann die Nullhypothese nicht verworfen werden und der Bauunternehmer schickt die Palette zurück.
Die Irrtumswahrscheinlichkeit gibt an, dass die Wahrscheinlichkeit dafür, die Nullhypothese fälschlicherweise zu verwerfen höchstens
b) (4)
 Wahrscheinlichkeit für ein irrtümliches Nichtablehnen berechnen
Hier sollst du die Wahrscheinlichkeit dafür berechnen, dass die Nullhypothese nicht verworfen wird, obwohl eigentlich die Wahrscheinlichkeit
Wahrscheinlichkeit für ein irrtümliches Nichtablehnen berechnen
Hier sollst du die Wahrscheinlichkeit dafür berechnen, dass die Nullhypothese nicht verworfen wird, obwohl eigentlich die Wahrscheinlichkeit  gilt, es sich also tatsächlich um A-Fliesen handelt. Dies entspricht der Wahrscheinlichkeit für den Fehler 2. Art. Betrachte hier also die Zufallsvariable
gilt, es sich also tatsächlich um A-Fliesen handelt. Dies entspricht der Wahrscheinlichkeit für den Fehler 2. Art. Betrachte hier also die Zufallsvariable  von eben, allerdings unter der Voraussetzung, dass tatsächlich
von eben, allerdings unter der Voraussetzung, dass tatsächlich  gilt. Dann ist die gesuchte Wahrscheinlichkeit
gilt. Dann ist die gesuchte Wahrscheinlichkeit  , die du wieder wie zuvor mit der Tabelle zur kumulierten Binomialverteilung oder deinem GTR berechnen kannst, nachdem du den Term mit Hilfe des Gegenereignisses umgeformt hast:
, die du wieder wie zuvor mit der Tabelle zur kumulierten Binomialverteilung oder deinem GTR berechnen kannst, nachdem du den Term mit Hilfe des Gegenereignisses umgeformt hast:
![\(\begin{array}[t]{rll}
P_{p=0,1}(X \geq 14)&=& 1- P_{p=0,1}(X\leq 13) &\quad \scriptsize \\[5pt]
&\approx&1- 0,8761&\quad \scriptsize \\[5pt]
&=& 0,1239&\quad \scriptsize \\[5pt]
&=&12,39\,\% &\quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/7d26353b0bf9b8375ff36301c8d6992c14fe23a2dd04918a1ed25cd41018adbb?color=5a5a5a) Die Wahrscheinlichkeit dafür, die Hypothese irrtümlich beizubehalten, obwohl eigentlich die alternative Wahrscheinlichkeit
Die Wahrscheinlichkeit dafür, die Hypothese irrtümlich beizubehalten, obwohl eigentlich die alternative Wahrscheinlichkeit  gilt, also eine Palette mit A-Fliesen versehentlich zurückzuschicken, beträgt ca.
gilt, also eine Palette mit A-Fliesen versehentlich zurückzuschicken, beträgt ca.  .
.
 Wahrscheinlichkeit für eine irrtümliche Ablehnung der Nullhypothese berechnen
Die Wahrscheinlichkeit dafür, die Nullhypothese fälschlicherweise abzulehnen ist genau die Wahrscheinlichkeit für den Fehler 1. Art und ergibt sich somit als
Wahrscheinlichkeit für eine irrtümliche Ablehnung der Nullhypothese berechnen
Die Wahrscheinlichkeit dafür, die Nullhypothese fälschlicherweise abzulehnen ist genau die Wahrscheinlichkeit für den Fehler 1. Art und ergibt sich somit als  .
.
In der Tabelle zur kumulierten Binomialverteilung findest du den Wert .
Die Wahrscheinlichkeit dafür, die Nullhypothese fälschlicherweise abzulehnen, beträgt ca.
.
Die Wahrscheinlichkeit dafür, die Nullhypothese fälschlicherweise abzulehnen, beträgt ca.  .
.
In der Tabelle zur kumulierten Binomialverteilung findest du den Wert
b) (5)
 Ermitteln der gesamten Irrtumswahrscheinlichkeit
Die gesamte Irrtumswahrscheinlichkeit setzt sich zusammen aus den beiden Wahrscheinlichkeiten aus dem vorherigen Aufgabenteil,
Ermitteln der gesamten Irrtumswahrscheinlichkeit
Die gesamte Irrtumswahrscheinlichkeit setzt sich zusammen aus den beiden Wahrscheinlichkeiten aus dem vorherigen Aufgabenteil,  und
und  , die den Wahrscheinlichkeiten für den Fehler 1. Art und für den Fehler 2. Art entsprechen. Allerdings muss dabei berücksichtigt werden, dass die Palette zufällig aus den 10 vorhandenen Paletten ausgewählt wurde. Der Fehler 1. Art kann nur begangen werden, wenn eine Palette mit B-Fliesen ausgewählt wurde und der Fehler 2. Art kann nur begangen werden, wenn eine Palette mit A-Fliesen ausgewählt wurde. Es handelt sich hier also um ein zweistufiges Zufallsexperiment. Du musst also die entsprechenden Wahrscheinlichkeiten für eine Palette mit A-Fliesen und für eine Palette mit B-Fliesen berücksichtigen, insgesamt ergibt sich dann mit den beiden Pfadregeln die folgende Wahrscheinlichkeit:
, die den Wahrscheinlichkeiten für den Fehler 1. Art und für den Fehler 2. Art entsprechen. Allerdings muss dabei berücksichtigt werden, dass die Palette zufällig aus den 10 vorhandenen Paletten ausgewählt wurde. Der Fehler 1. Art kann nur begangen werden, wenn eine Palette mit B-Fliesen ausgewählt wurde und der Fehler 2. Art kann nur begangen werden, wenn eine Palette mit A-Fliesen ausgewählt wurde. Es handelt sich hier also um ein zweistufiges Zufallsexperiment. Du musst also die entsprechenden Wahrscheinlichkeiten für eine Palette mit A-Fliesen und für eine Palette mit B-Fliesen berücksichtigen, insgesamt ergibt sich dann mit den beiden Pfadregeln die folgende Wahrscheinlichkeit:
 Die gesamte Irrtumswahrscheinlichkeit beträgt
Die gesamte Irrtumswahrscheinlichkeit beträgt  .
.
c) (1)
 Graphische Darstellung
Du sollst hier die neue Situation, die sich durch die Einführung der Testmaschine ergeben hat, graphisch darstellen. Für eine übersichtlichere Darstellung kannst du zunächst folgende oder ähnliche Bezeichnungen einführen:
Graphische Darstellung
Du sollst hier die neue Situation, die sich durch die Einführung der Testmaschine ergeben hat, graphisch darstellen. Für eine übersichtlichere Darstellung kannst du zunächst folgende oder ähnliche Bezeichnungen einführen:
 Lösungsweg A: Baumdiagramm
Um die Situation mit Hilfe eines Baumdiagramms darzustellen, überlege dir zunächst, wie viele Stufen hier vorliegen und gehe dann in jeder Stufe jede Möglichkeit durch.
Die erste Stufe ist die Produktion der Fliesen von Maschine A. Hier wird jede Fliese zur „1. Wahl“-Fliese oder „2. Wahl“-Fliese. Die Wahrscheinlichkeiten sind dementsprechend die Wahrscheinlichkeit dafür, dass Maschine A eine „1. Wahl“- bzw. „2. Wahl“-Fliese produziert.
Die nächste Stufe ist dann die Sortierung der Testmaschine. Diese hängt von der ersten Stufe ab. Die Wahrscheinlichkeiten in dieser Stufe kannst du der Aufgabenstellung entnehmen bzw. mit Hilfe des Gegenereignisses berechnen. Insgesamt besteht das Zufallsexperiment hier also aus 2 Stufen und das Baumdiagramm ergibt sich nun wie folgt:
Lösungsweg A: Baumdiagramm
Um die Situation mit Hilfe eines Baumdiagramms darzustellen, überlege dir zunächst, wie viele Stufen hier vorliegen und gehe dann in jeder Stufe jede Möglichkeit durch.
Die erste Stufe ist die Produktion der Fliesen von Maschine A. Hier wird jede Fliese zur „1. Wahl“-Fliese oder „2. Wahl“-Fliese. Die Wahrscheinlichkeiten sind dementsprechend die Wahrscheinlichkeit dafür, dass Maschine A eine „1. Wahl“- bzw. „2. Wahl“-Fliese produziert.
Die nächste Stufe ist dann die Sortierung der Testmaschine. Diese hängt von der ersten Stufe ab. Die Wahrscheinlichkeiten in dieser Stufe kannst du der Aufgabenstellung entnehmen bzw. mit Hilfe des Gegenereignisses berechnen. Insgesamt besteht das Zufallsexperiment hier also aus 2 Stufen und das Baumdiagramm ergibt sich nun wie folgt:
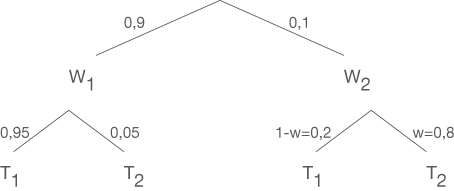
 Lösungsweg B: Vierfeldertafel
Beginne bei der Vierfeldertafel damit die Wahrscheinlichkeiten einzutragen, die du direkt der Aufgabenstellung entnehmen kannst. Fülle anschließend die Vierfeldertafel auf, indem du aus den bekannten Wahrscheinlichkeiten die übrigen Wahrscheinlichkeiten bestimmst. Beachte dabei, dass sich der Eintrag einer Vierfeldertafel in der Spalte zu Ereignis
Lösungsweg B: Vierfeldertafel
Beginne bei der Vierfeldertafel damit die Wahrscheinlichkeiten einzutragen, die du direkt der Aufgabenstellung entnehmen kannst. Fülle anschließend die Vierfeldertafel auf, indem du aus den bekannten Wahrscheinlichkeiten die übrigen Wahrscheinlichkeiten bestimmst. Beachte dabei, dass sich der Eintrag einer Vierfeldertafel in der Spalte zu Ereignis  und in der Zeile zu Ereignis
und in der Zeile zu Ereignis  aus
aus  ergibt. Es gilt
ergibt. Es gilt
 Es geht hier also um bedingte Wahrscheinlichkeiten. Daraus kannst du folgende Wahrscheinlichkeiten mit Hilfe des Gegenereignisses berechnen:
Es geht hier also um bedingte Wahrscheinlichkeiten. Daraus kannst du folgende Wahrscheinlichkeiten mit Hilfe des Gegenereignisses berechnen:
 und
und  Damit ergibt sich nun folgendes:
Damit ergibt sich nun folgendes:
 Wahrscheinlichkeit berechnen
Du sollst hier die Wahrscheinlichkeit dafür berechnen, dass eine zufällig ausgewählte Fliese als 1. Wahl eingestuft wird. Gesucht ist also
Wahrscheinlichkeit berechnen
Du sollst hier die Wahrscheinlichkeit dafür berechnen, dass eine zufällig ausgewählte Fliese als 1. Wahl eingestuft wird. Gesucht ist also  . Je nachdem welchen Lösungsweg du im letzten Aufgabenteil gewählt hast, unterscheidet sich auch hier der Lösungsweg.
. Je nachdem welchen Lösungsweg du im letzten Aufgabenteil gewählt hast, unterscheidet sich auch hier der Lösungsweg.
 Lösungsweg A: Baumdiagramm
Die gesuchte Wahrscheinlichkeit ergibt sich hier mit den Pfadregeln:
Lösungsweg A: Baumdiagramm
Die gesuchte Wahrscheinlichkeit ergibt sich hier mit den Pfadregeln:
![\(\begin{array}[t]{rll}
P(T_1)&=&P(T_1\mid W_1)\cdot P(W_1) + P(T_1\mid W_2)\cdot W_2 \quad \scriptsize \\[5pt]
&=&0,9\cdot 0,95+ 0,1\cdot 0,2 \quad \scriptsize \\[5pt]
&=&0,875 \quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/da25ef292b6f1e207ea5529b89c1acef3aaa6b2f1be4a48657d701efbc6609cf?color=5a5a5a) Mit einer Wahrscheinlichkeit von
Mit einer Wahrscheinlichkeit von  wird eine zufällig ausgewählte Fliese aus Maschine A von der Testmaschine als 1. Wahl eingestuft und somit nicht aussortiert.
wird eine zufällig ausgewählte Fliese aus Maschine A von der Testmaschine als 1. Wahl eingestuft und somit nicht aussortiert.
 Lösungsweg B: Vierfeldertafel
Mit Hilfe der Vierfeldertafel, kannst du die gesuchte Wahrscheinlichkeit direkt ablesen:
Lösungsweg B: Vierfeldertafel
Mit Hilfe der Vierfeldertafel, kannst du die gesuchte Wahrscheinlichkeit direkt ablesen:
 Mit einer Wahrscheinlichkeit von
Mit einer Wahrscheinlichkeit von  wird eine zufällig ausgewählte Fliese aus Maschine A von der Testmaschine als 1. Wahl eingestuft und somit nicht aussortiert.
wird eine zufällig ausgewählte Fliese aus Maschine A von der Testmaschine als 1. Wahl eingestuft und somit nicht aussortiert.
: Die vorliegende Fliese ist 1. Wahl
: Die vorliegende Fliese ist 2. Wahl
: Die vorliegende Fliese wird von der Testmaschine als 1. Wahl bezeichnet
: Die vorliegende Fliese wird von der Testmaschine als 2. Wahl bezeichnet

| Summe | |||
|---|---|---|---|
| Summe |
c) (2)
 Wahrscheinlichkeit berechnen
Hier sollst du nun die Wahrscheinlichkeit dafür berechnen, dass eine Fliese eine „2. Wahl“-Fliese ist unter der Bedingung, dass sie von der Maschine nicht aussortiert wurde, also als 1. Wahl eingestuft wurde. Gesucht ist also
Wahrscheinlichkeit berechnen
Hier sollst du nun die Wahrscheinlichkeit dafür berechnen, dass eine Fliese eine „2. Wahl“-Fliese ist unter der Bedingung, dass sie von der Maschine nicht aussortiert wurde, also als 1. Wahl eingestuft wurde. Gesucht ist also  . Du kannst hier den Satz von Bayes verwenden:
. Du kannst hier den Satz von Bayes verwenden:
 Damit ergibt sich dann:
Damit ergibt sich dann:
![\(\begin{array}[t]{rll}
P(W_2 \mid T_1) &=& \dfrac{P(T_1\mid W_2)\cdot P(W_2)}{P(T_1)} \quad \scriptsize \\[5pt]
&=& \dfrac{0,1\cdot 0,2}{0,875}\quad \scriptsize \\[5pt]
&\approx&0,0229 \quad \scriptsize \\[5pt]
&=&2,29\,\% \quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/68a81c39bb3e855651068f46c4b8983af70a9d7c526315941115738dfbaa8b97?color=5a5a5a) Mit einer Wahrscheinlichkeit von ca.
Mit einer Wahrscheinlichkeit von ca.  ist eine nicht aussortierte Fliese eine „2. Wahl“-Fliese.
ist eine nicht aussortierte Fliese eine „2. Wahl“-Fliese.
c) (3)
 Aussortierwahrscheinlichkeit berechnen
Gesucht ist hier
Aussortierwahrscheinlichkeit berechnen
Gesucht ist hier  , sodass die Wahrscheinlichkeit
, sodass die Wahrscheinlichkeit  kleiner als
kleiner als  ist. Mit der Gleichung aus der letzten Aufgabe ergibt sich folgendes:
ist. Mit der Gleichung aus der letzten Aufgabe ergibt sich folgendes:
![\(\begin{array}[t]{rll}
P(W_2\mid T_1)& \lt &0,01 \quad \scriptsize \\[5pt]
\dfrac{P(T_1\mid W_2)\cdot P(W_2)}{P(T_1)} & \lt &0,01 \quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/46b3639eed4ee0853d90ebe7b2b99b62f4d12118946515ca8a7a526222b5dc15?color=5a5a5a) Bestimme nun die einzelnen Bestandteile dieser Ungleichung für allgemeines
Bestimme nun die einzelnen Bestandteile dieser Ungleichung für allgemeines  , um anschließend einsetzen und nach
, um anschließend einsetzen und nach  lösen zu können.
Es gilt
lösen zu können.
Es gilt  und damit
und damit  . Wegen
. Wegen  gilt nun:
gilt nun:
 Einsetzen ergibt nun:
Einsetzen ergibt nun:
![\(\begin{array}[t]{rll}
\dfrac{P(T_1\mid W_2)\cdot P(W_2)}{P(T_1)} &\lt & 0,01\quad \scriptsize \\[5pt]
\dfrac{(1-w)\cdot 0,1}{ 0,855 + (1-w)\cdot 0,1}&\lt &0,01 &\quad \scriptsize \mid\;\cdot (0,855 + (1-w)\cdot 0,1) \\[5pt]
(1-w)\cdot 0,1&\lt & 0,00855 + (1-w)\cdot 0,001 &\quad \scriptsize \mid\; - 0,001(1-w) \\[5pt]
0,099(1-w) &\lt & 0,00855 &\quad \scriptsize \mid\; : 0,099\\[5pt]
1-w&\lt & \frac{19}{220}&\quad \scriptsize \mid\; +w \\[5pt]
1 &\lt & \frac{19}{220} +w&\quad \scriptsize \mid\;- \frac{19}{220} \\[5pt]
\frac{201}{220}&\lt &w &\quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/0aa1912ead17e05607d2d0421ae7b4c8474193473f09010ddbd6be3cbf4c2a7b?color=5a5a5a) Insgesamt muss also
Insgesamt muss also  gelten, damit die Wahrscheinlichkeit für eine fälschlicherweise nicht aussortierte Fliese 2. Wahl unter
gelten, damit die Wahrscheinlichkeit für eine fälschlicherweise nicht aussortierte Fliese 2. Wahl unter  sinkt.
sinkt.
a)(1)
 Bestimmen der Wahrscheinlichkeit
Du sollst die Wahrscheinlichkeit dafür berechnen, dass in einer Packung A-Fliesen, die aus 20 Fliesen von Maschine A besteht, genau zwei „2.Wahl“-Fliesen enthalten sind.
Betrachte dazu die Zufallsvariable
Bestimmen der Wahrscheinlichkeit
Du sollst die Wahrscheinlichkeit dafür berechnen, dass in einer Packung A-Fliesen, die aus 20 Fliesen von Maschine A besteht, genau zwei „2.Wahl“-Fliesen enthalten sind.
Betrachte dazu die Zufallsvariable  , die die Anzahl der „2. Wahl“-Fliesen in einer zufällig ausgewählten Packung von A-Fliesen beschreibt. Gesucht ist nun die Wahrscheinlichkeit
, die die Anzahl der „2. Wahl“-Fliesen in einer zufällig ausgewählten Packung von A-Fliesen beschreibt. Gesucht ist nun die Wahrscheinlichkeit
 Da in der Aufgabenstellung angegeben ist, dass die Produktion stochastisch unabhängig ist und man davon ausgehen kann, dass jede Fliese von Maschine A die gleiche Wahrscheinlichkeit besitzt „2. Wahl“ oder „1. Wahl“ zu sein, kannst du davon ausgehen, dass
Da in der Aufgabenstellung angegeben ist, dass die Produktion stochastisch unabhängig ist und man davon ausgehen kann, dass jede Fliese von Maschine A die gleiche Wahrscheinlichkeit besitzt „2. Wahl“ oder „1. Wahl“ zu sein, kannst du davon ausgehen, dass  binomialverteilt ist. Die Parameter lauten hier
binomialverteilt ist. Die Parameter lauten hier  und
und  . Die gesuchte Wahrscheinlichkeit kannst du dann entweder mit der Formel für die Binomialverteilung oder deinem GTR berechnen.
. Die gesuchte Wahrscheinlichkeit kannst du dann entweder mit der Formel für die Binomialverteilung oder deinem GTR berechnen.
 Lösungsweg A: GTR
Du kannst den binompdf-Befehl deines GTR verwenden. Diesen findest du im STAT-Menü unter
Lösungsweg A: GTR
Du kannst den binompdf-Befehl deines GTR verwenden. Diesen findest du im STAT-Menü unter
 ,
,  und
und  eingeben. Du erhältst dann das Ergebnis
eingeben. Du erhältst dann das Ergebnis  .
.
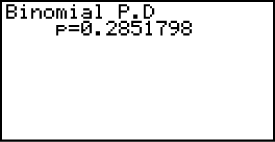 Mit einer Wahrscheinlichkeit von
Mit einer Wahrscheinlichkeit von  sind in einer Packung A-Fliesen genau 2 „2. Wahl“-Fliesen enthalten.
sind in einer Packung A-Fliesen genau 2 „2. Wahl“-Fliesen enthalten.
 Lösungsweg B: Handschriftlich
Für eine binomialverteilte Zufallsvariable
Lösungsweg B: Handschriftlich
Für eine binomialverteilte Zufallsvariable  mit den Parametern
mit den Parametern  und
und  gilt:
gilt:
 Setze dort nun die entsprechenden Werte ein und erhalte so folgendes:
Setze dort nun die entsprechenden Werte ein und erhalte so folgendes:
![\(\begin{array}[t]{rll}
P(X=2)&=&\binom{20}{2}\cdot 0,1^2\cdot (1-0,1)^{20-2} &\quad \scriptsize \\[5pt]
&=& \binom{20}{2}\cdot 0,1^2\cdot 0,9^{18}&\quad \scriptsize \\[5pt]
&\approx&0,2852 &\quad \scriptsize \\[5pt]
&=&28,52\,\% &\quad \scriptsize \\
\end{array}\)](https://mathjax.schullv.de/73070678ba03add762b08f9a785429df264a0e67b8ea22f133646fb1b1598c03?color=5a5a5a) Mit einer Wahrscheinlichkeit von
Mit einer Wahrscheinlichkeit von  sind in einer Packung A-Fliesen genau 2 „2. Wahl“-Fliesen enthalten.
sind in einer Packung A-Fliesen genau 2 „2. Wahl“-Fliesen enthalten.
F5: DIST  F5: BINM
F5: BINM  F1: pdf
F1: pdf  F2: Var
F2: Var
Du musst dann die entsprechenden Parameter 
a) (2)
 Wahrscheinlichkeit bestimmen
Nun sollst du die Wahrscheinlichkeit dafür berechnen, dass in einer Packung A-Fliesen maximal
Wahrscheinlichkeit bestimmen
Nun sollst du die Wahrscheinlichkeit dafür berechnen, dass in einer Packung A-Fliesen maximal  der Fliesen „1.Wahl“-Fliesen sind. Berechne dazu zunächst wie viele Fliesen es demnach höchstens sein dürfen um die
der Fliesen „1.Wahl“-Fliesen sind. Berechne dazu zunächst wie viele Fliesen es demnach höchstens sein dürfen um die  -Grenze nicht zu überschreiten und forme diese Aussage in eine Aussage über die „2. Wahl“-Fliesen um. Betrachtest du dann wieder die Zufallsvariable
-Grenze nicht zu überschreiten und forme diese Aussage in eine Aussage über die „2. Wahl“-Fliesen um. Betrachtest du dann wieder die Zufallsvariable  , so hat die gesuchte Wahrscheinlichkeit die Form
, so hat die gesuchte Wahrscheinlichkeit die Form  . Du kannst nun die kumulierte Binomialverteilung verwenden.
1. Schritt: Maximale Anzahl an „1. Wahl“-Fliesen berechnen
Maximal
. Du kannst nun die kumulierte Binomialverteilung verwenden.
1. Schritt: Maximale Anzahl an „1. Wahl“-Fliesen berechnen
Maximal  der Fliesen sollen „1. Wahl“-Fliesen sein:
der Fliesen sollen „1. Wahl“-Fliesen sein:
 Es sollen maximal
Es sollen maximal  Fliesen aus der Packung mit 20 Fliesen „1. Wahl“-Fliesen sein. Dies ist genau dann der Fall, wenn sich mindestens
Fliesen aus der Packung mit 20 Fliesen „1. Wahl“-Fliesen sein. Dies ist genau dann der Fall, wenn sich mindestens  „2. Wahl“-Fliesen in der Packung befinden. Gesucht ist also die Wahrscheinlichkeit
„2. Wahl“-Fliesen in der Packung befinden. Gesucht ist also die Wahrscheinlichkeit  .
2. Schritt: Wahrscheinlichkeit berechnen
Bringe die gesuchte Wahrscheinlichkeit zunächst mit Hilfe des Gegenereignisses in eine Form der Art
.
2. Schritt: Wahrscheinlichkeit berechnen
Bringe die gesuchte Wahrscheinlichkeit zunächst mit Hilfe des Gegenereignisses in eine Form der Art  , damit du die Tabelle zur kumulierten Binomialverteilung oder den binomcdf-Befehl deines GTR verwenden kannst:
, damit du die Tabelle zur kumulierten Binomialverteilung oder den binomcdf-Befehl deines GTR verwenden kannst:

 Lösungsweg A: GTR
Den binomcdf-Befehl deines GTR findest du unter
Lösungsweg A: GTR
Den binomcdf-Befehl deines GTR findest du unter
 Mit einer Wahrscheinlichkeit von ca.
Mit einer Wahrscheinlichkeit von ca.  befinden sich in einer Packung A-Fliesen höchstens
befinden sich in einer Packung A-Fliesen höchstens  „1. Wahl“-Fliesen.
„1. Wahl“-Fliesen.
 Lösungsweg B: Tabelle
Lies aus der Tabelle zur kummulierten Binomialverteilung für
Lösungsweg B: Tabelle
Lies aus der Tabelle zur kummulierten Binomialverteilung für  den Wert aus der Spalte für
den Wert aus der Spalte für  und der Zeile für
und der Zeile für  ab. So erhältst du folgendes Ergebnis:
ab. So erhältst du folgendes Ergebnis:
 .
Mit einer Wahrscheinlichkeit von ca.
.
Mit einer Wahrscheinlichkeit von ca.  befinden sich in einer Packung A-Fliesen höchstens
befinden sich in einer Packung A-Fliesen höchstens  „1. Wahl“-Fliesen.
„1. Wahl“-Fliesen.
2ND  VARS(DISTR)
VARS(DISTR)  B: binomcdf
B: binomcdf
Dort musst du nun wie oben die entsprechenden Parameter eingeben und erhältst dann das folgende Ergebnis
a) (3)
 Wahrscheinlichkeit berechnen
Du sollst die Wahrscheinlichkeit dafür berechnen, dass alle Fliesen in einer zufällig ausgewählten Reihe, die aus
Wahrscheinlichkeit berechnen
Du sollst die Wahrscheinlichkeit dafür berechnen, dass alle Fliesen in einer zufällig ausgewählten Reihe, die aus  Fliesen besteht, „1. Wahl“-Fliesen sind. Betrachte dazu die Zufallsvariable
Fliesen besteht, „1. Wahl“-Fliesen sind. Betrachte dazu die Zufallsvariable  , die die Anzahl der „1. Wahl“-Fliesen in einer Reihe beschreibt. Diese ist aus den gleichen Gründen wie
, die die Anzahl der „1. Wahl“-Fliesen in einer Reihe beschreibt. Diese ist aus den gleichen Gründen wie  binomialverteilt, allerdings mit den Parametern
binomialverteilt, allerdings mit den Parametern  und
und  .
.
Gesucht ist dann die Wahrscheinlichkeit . Diese lässt sich wieder mit der Formel für die Binomialverteilung oder dem Binompdf-Befehl deines GTR berechnen. In beiden Fällen erhältst du folgendes Ergebnis:
. Diese lässt sich wieder mit der Formel für die Binomialverteilung oder dem Binompdf-Befehl deines GTR berechnen. In beiden Fällen erhältst du folgendes Ergebnis:
![\(\begin{array}[t]{rll}
P(Y=5)&=&\binom{5}{5}\cdot 0,8^5\cdot 0,2^0 &\quad \scriptsize \\[5pt]
&=& 0,8 ^5 &\quad \scriptsize \\[5pt]
&\approx& 0,32768 &\quad \scriptsize \\[5pt]
&=& 32,768\,\% &\quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/c104175ef9d434ca20e764ca6702dc4ab35ceab81f3444760120267cf905ecfa?color=5a5a5a) Mit einer Wahrscheinlichkeit von ca.
Mit einer Wahrscheinlichkeit von ca.  besteht eine zufällig ausgewählte Reihe nur aus „1. Wahl“-Fliesen .
besteht eine zufällig ausgewählte Reihe nur aus „1. Wahl“-Fliesen .
Gesucht ist dann die Wahrscheinlichkeit
a) (4)
 Wahrscheinlichkeit berechnen
Hier sollst du nun die Wahrscheinlichkeit dafür berechnen, dass es unter den
Wahrscheinlichkeit berechnen
Hier sollst du nun die Wahrscheinlichkeit dafür berechnen, dass es unter den  Reihen mindestens eine gibt, die nur „1. Wahl“-Fliesen enthält. Betrachte dazu die Zufallsvariable
Reihen mindestens eine gibt, die nur „1. Wahl“-Fliesen enthält. Betrachte dazu die Zufallsvariable  , die die zufällige Anzahl der Reihen beschreibt, die nur aus „1. Wahl“-Fliesen bestehen. Dann ist
, die die zufällige Anzahl der Reihen beschreibt, die nur aus „1. Wahl“-Fliesen bestehen. Dann ist  binomialverteilt mit den Parametern
binomialverteilt mit den Parametern  und
und  , da jede Reihe die gleiche Wahrscheinlichkeit besitzt nur aus „1. Wahl“-Fliesen zu bestehen und die Besetzung einer Reihe nicht von der Besetzung der übrigen Reihen abhängt.
Gesucht ist demnach nun die Wahrscheinlichkeit
, da jede Reihe die gleiche Wahrscheinlichkeit besitzt nur aus „1. Wahl“-Fliesen zu bestehen und die Besetzung einer Reihe nicht von der Besetzung der übrigen Reihen abhängt.
Gesucht ist demnach nun die Wahrscheinlichkeit  , welche du wieder wie oben berechnen kannst:
, welche du wieder wie oben berechnen kannst:
![\(\begin{array}[t]{rll}
P(R \geq 1)&=&1- P(R \leq 0) &\quad \scriptsize\\[5pt]
&=& 1-P(R =0)&\quad \scriptsize \\[5pt]
&=&1- \binom{4}{0}\cdot 0, 32768^0\cdot (1-0, 32768)^4 &\quad \scriptsize \\[5pt]
&\approx&0,7957 &\quad \scriptsize \\[5pt]
&=&79,57\,\% &\quad \scriptsize \\
\end{array}\)](https://mathjax.schullv.de/90b49f4577ba2528557f12728bd1f01116ea7d6bef18dcc5350026e23e647d64?color=5a5a5a) Mit einer Wahrscheinlichkeit von ca.
Mit einer Wahrscheinlichkeit von ca.  gibt es unter den
gibt es unter den  Reihen mindestens eine Reihe, die nur aus „1. Wahl“-Fliesen besteht.
Reihen mindestens eine Reihe, die nur aus „1. Wahl“-Fliesen besteht.
b) (1)
 Binomialverteilung begründen
In diesem Aufgabenteil wird die Zufallsvariable
Binomialverteilung begründen
In diesem Aufgabenteil wird die Zufallsvariable  betrachtet, die die zufällige Anzahl der „2. Wahl“-Fliesen in einer Stichprobe mit
betrachtet, die die zufällige Anzahl der „2. Wahl“-Fliesen in einer Stichprobe mit  Fliesen aus einer Palette beschreibt. Du sollst nun begründen, warum
Fliesen aus einer Palette beschreibt. Du sollst nun begründen, warum  als binomialverteilt angenommen werden kann und erklären, dass dann entweder
als binomialverteilt angenommen werden kann und erklären, dass dann entweder  oder
oder  gilt.
Für eine binomialverteilte Zufallsgröße, müssen folgende Eigenschaften erfüllt sein:
gilt.
Für eine binomialverteilte Zufallsgröße, müssen folgende Eigenschaften erfüllt sein:
 erfüllt sind und betrachte anschließend den Parameter
erfüllt sind und betrachte anschließend den Parameter  .
Im vorliegenden Fall, besteht ein einzelnes Zufallsexperiment darin eine zufällig ausgewählte Fliese zu betrachten und den „1. Wahl“-Fliesen oder den „2. Wahl“-Fliesen zuzuordnen. Es gibt also auch nur diese beiden Möglichkeiten, eine Fliese muss entweder „1. Wahl“ oder „2. Wahl“ sein und kann nicht nichts von beidem oder beides sein. Man kann dabei „1. Wahl“-Fliesen als „Misserfolg“ und „2. Wahl“-Fliesen als „Erfolg“ bezeichnen. Damit ist die dritte Eigenschaft erfüllt.
Die erste Eigenschaft ist auch erfüllt, dies kannst du dem Einleitungstext der Aufgabe entnehmen. Danach ist die Produktion einer Fliese stochastisch unabhängig von der Produktion der anderen Fliesen.
Eine Palette enthält immer entweder nur A-Fliesen oder nur B-Fliesen, da eine Palette immer aus Fliesen von derselben Maschine besteht. Demnach hat auch jede Fliese aus einer Palette die gleiche Wahrscheinlichkeit eine „1. Wahl“-Fliese oder eine „2. Wahl“-Fliese zu sein. In dem Fall, dass die Fliesen der Palette aus Maschine A stammen, beträgt die Wahrscheinlichkeit dafür, dass eine Fliese „2. Wahl“ ist,
.
Im vorliegenden Fall, besteht ein einzelnes Zufallsexperiment darin eine zufällig ausgewählte Fliese zu betrachten und den „1. Wahl“-Fliesen oder den „2. Wahl“-Fliesen zuzuordnen. Es gibt also auch nur diese beiden Möglichkeiten, eine Fliese muss entweder „1. Wahl“ oder „2. Wahl“ sein und kann nicht nichts von beidem oder beides sein. Man kann dabei „1. Wahl“-Fliesen als „Misserfolg“ und „2. Wahl“-Fliesen als „Erfolg“ bezeichnen. Damit ist die dritte Eigenschaft erfüllt.
Die erste Eigenschaft ist auch erfüllt, dies kannst du dem Einleitungstext der Aufgabe entnehmen. Danach ist die Produktion einer Fliese stochastisch unabhängig von der Produktion der anderen Fliesen.
Eine Palette enthält immer entweder nur A-Fliesen oder nur B-Fliesen, da eine Palette immer aus Fliesen von derselben Maschine besteht. Demnach hat auch jede Fliese aus einer Palette die gleiche Wahrscheinlichkeit eine „1. Wahl“-Fliese oder eine „2. Wahl“-Fliese zu sein. In dem Fall, dass die Fliesen der Palette aus Maschine A stammen, beträgt die Wahrscheinlichkeit dafür, dass eine Fliese „2. Wahl“ ist,  und bei Fliesen aus Maschine B beträgt diese Wahrscheinlichkeit
und bei Fliesen aus Maschine B beträgt diese Wahrscheinlichkeit  . Somit hast du sowohl die zweite Eigenschaft begründet, als auch die Trefferwahrscheinlichkeit erklärt.
. Somit hast du sowohl die zweite Eigenschaft begründet, als auch die Trefferwahrscheinlichkeit erklärt.
- Die
einzelnen Zufallsexperimente sind unabhängig voneinander
- Die Wahrscheinlichkeit
für einen Erfolg ist in jedem einzelnen Zufallsexperiment gleich
- In den einzelnen Zufallsexperimenten gibt es nur zwei mögliche Ergebnisse
b) (2)
 Wahl der Nullhypothese erklären
In dem Hypothesentest wird die Nullhypothese wie folgt gewählt:
Wahl der Nullhypothese erklären
In dem Hypothesentest wird die Nullhypothese wie folgt gewählt:
 Du sollst diese Wahl nun erklären. Überlege dir dazu zunächst für welche Werte diese Hypothese abgelehnt wird und welche Folgen die Bestätigung bzw. die Ablehnung der Nullhypothese für den Bauunternehmer hätte.
Die Nullhypothese wird nur für signifikant zu kleine Werte abgelehnt, also dann wenn in der Stichprobe signifikant wenige „2. Wahl“-Fliesen gefunden werden. In einem solchen Fall kann der Bauunternehmer davon ausgehen, dass die Wahrscheinlichkeit für eine Fliese 2. Wahl kleiner als
Du sollst diese Wahl nun erklären. Überlege dir dazu zunächst für welche Werte diese Hypothese abgelehnt wird und welche Folgen die Bestätigung bzw. die Ablehnung der Nullhypothese für den Bauunternehmer hätte.
Die Nullhypothese wird nur für signifikant zu kleine Werte abgelehnt, also dann wenn in der Stichprobe signifikant wenige „2. Wahl“-Fliesen gefunden werden. In einem solchen Fall kann der Bauunternehmer davon ausgehen, dass die Wahrscheinlichkeit für eine Fliese 2. Wahl kleiner als  ist und es sich nicht um eine Palette aus der Herstellung von Maschine B handelt. Dann nimmt der Bauunternehmer die Palette an.
ist und es sich nicht um eine Palette aus der Herstellung von Maschine B handelt. Dann nimmt der Bauunternehmer die Palette an.
Der Bauunternehmer möchte also sicher gehen und nur solche Paletten annehmen, bei denen der Anteil der „2. Wahl“-Fliesen signifikant kleiner als ist. In jedem anderen Fall schickt er die Palette zurück. Damit soll möglichst ausgeschlossen werden, dass fälschlicherweise eine Palette mit B-Fliesen angenommen wird.
ist. In jedem anderen Fall schickt er die Palette zurück. Damit soll möglichst ausgeschlossen werden, dass fälschlicherweise eine Palette mit B-Fliesen angenommen wird.
Der Bauunternehmer möchte also sicher gehen und nur solche Paletten annehmen, bei denen der Anteil der „2. Wahl“-Fliesen signifikant kleiner als
b) (3)
 Entscheidungsregel formulieren
In dieser Aufgabe sollst du nun eine Entscheidungsregel für den beschriebenen Hypothesentest auf Grundlage der Irrtumswahrscheinlichkeit von
Entscheidungsregel formulieren
In dieser Aufgabe sollst du nun eine Entscheidungsregel für den beschriebenen Hypothesentest auf Grundlage der Irrtumswahrscheinlichkeit von  formulieren. Gesucht ist also die größte Anzahl
formulieren. Gesucht ist also die größte Anzahl  von Fliesen zweiter Wahl, für die die Nullhypothese gerade noch verworfen wird.
Betrachte hier die in der Aufgabenstellung eingeführte Zufallsvariable
von Fliesen zweiter Wahl, für die die Nullhypothese gerade noch verworfen wird.
Betrachte hier die in der Aufgabenstellung eingeführte Zufallsvariable  , die nach b) (1) binomialverteilt ist mit den Parametern
, die nach b) (1) binomialverteilt ist mit den Parametern  und
und  .
.
Die Irrtumswahrscheinlichkeit gibt an, dass die Wahrscheinlichkeit dafür, die Nullhypothese fälschlicherweise zu verwerfen höchstens betragen soll. Daraus ergibt sich folgende Ungleichung, aus der du den Wert
betragen soll. Daraus ergibt sich folgende Ungleichung, aus der du den Wert  berechnen kannst, für den die Nullhypothese gerade noch verworfen werden soll:
berechnen kannst, für den die Nullhypothese gerade noch verworfen werden soll:
 für alle
für alle  Da im vorliegenden Fall nur
Da im vorliegenden Fall nur  oder
oder  gelten kann, kannst du die Ungleichung unter der Annahme betrachten, dass laut Nullhypothese
gelten kann, kannst du die Ungleichung unter der Annahme betrachten, dass laut Nullhypothese  gilt. Du erhältst dann einen Wert für
gilt. Du erhältst dann einen Wert für  , indem du die Tabelle zur kumulierten Binomialverteilung „rückwärts“ anwendest. Suche in der Tabelle zu
, indem du die Tabelle zur kumulierten Binomialverteilung „rückwärts“ anwendest. Suche in der Tabelle zu  in der Spalte zu
in der Spalte zu  nach dem größten
nach dem größten  , bei dem der Tabelleneintrag gerade noch
, bei dem der Tabelleneintrag gerade noch  0,05 ist. Dann findest du folgendes:
0,05 ist. Dann findest du folgendes:
 .
Die Entscheidungsregel lautet demach wie folgt:
Werden in der Stichprobe von
.
Die Entscheidungsregel lautet demach wie folgt:
Werden in der Stichprobe von  Fliesen höchstens
Fliesen höchstens  Fliesen 2. Wahl gefunden , wird die Nullhypothese auf Grundlage der Irrtumswahrscheinlichkeit von
Fliesen 2. Wahl gefunden , wird die Nullhypothese auf Grundlage der Irrtumswahrscheinlichkeit von  verworfen und der Bauunternehmer schickt die Palette nicht zurück. Werden mehr als
verworfen und der Bauunternehmer schickt die Palette nicht zurück. Werden mehr als  Fliesen 2. Wahl gefunden, kann die Nullhypothese nicht verworfen werden und der Bauunternehmer schickt die Palette zurück.
Fliesen 2. Wahl gefunden, kann die Nullhypothese nicht verworfen werden und der Bauunternehmer schickt die Palette zurück.
Die Irrtumswahrscheinlichkeit gibt an, dass die Wahrscheinlichkeit dafür, die Nullhypothese fälschlicherweise zu verwerfen höchstens
b) (4)
 Wahrscheinlichkeit für ein irrtümliches Nichtablehnen berechnen
Hier sollst du die Wahrscheinlichkeit dafür berechnen, dass die Nullhypothese nicht verworfen wird, obwohl eigentlich die Wahrscheinlichkeit
Wahrscheinlichkeit für ein irrtümliches Nichtablehnen berechnen
Hier sollst du die Wahrscheinlichkeit dafür berechnen, dass die Nullhypothese nicht verworfen wird, obwohl eigentlich die Wahrscheinlichkeit  gilt, es sich also tatsächlich um A-Fliesen handelt. Dies entspricht der Wahrscheinlichkeit für den Fehler 2. Art. Betrachte hier also die Zufallsvariable
gilt, es sich also tatsächlich um A-Fliesen handelt. Dies entspricht der Wahrscheinlichkeit für den Fehler 2. Art. Betrachte hier also die Zufallsvariable  von eben, allerdings unter der Voraussetzung, dass tatsächlich
von eben, allerdings unter der Voraussetzung, dass tatsächlich  gilt. Dann ist die gesuchte Wahrscheinlichkeit
gilt. Dann ist die gesuchte Wahrscheinlichkeit  , die du wieder wie zuvor mit der Tabelle zur kumulierten Binomialverteilung oder deinem GTR berechnen kannst, nachdem du den Term mit Hilfe des Gegenereignisses umgeformt hast:
, die du wieder wie zuvor mit der Tabelle zur kumulierten Binomialverteilung oder deinem GTR berechnen kannst, nachdem du den Term mit Hilfe des Gegenereignisses umgeformt hast:
![\(\begin{array}[t]{rll}
P_{p=0,1}(X \geq 14)&=& 1- P_{p=0,1}(X\leq 13) &\quad \scriptsize \\[5pt]
&\approx&1- 0,8761&\quad \scriptsize \\[5pt]
&=& 0,1239&\quad \scriptsize \\[5pt]
&=&12,39\,\% &\quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/7d26353b0bf9b8375ff36301c8d6992c14fe23a2dd04918a1ed25cd41018adbb?color=5a5a5a) Die Wahrscheinlichkeit dafür, die Hypothese irrtümlich beizubehalten, obwohl eigentlich die alternative Wahrscheinlichkeit
Die Wahrscheinlichkeit dafür, die Hypothese irrtümlich beizubehalten, obwohl eigentlich die alternative Wahrscheinlichkeit  gilt, also eine Palette mit A-Fliesen versehentlich zurückzuschicken, beträgt ca.
gilt, also eine Palette mit A-Fliesen versehentlich zurückzuschicken, beträgt ca.  .
.
 Wahrscheinlichkeit für eine irrtümliche Ablehnung der Nullhypothese berechnen
Die Wahrscheinlichkeit dafür, die Nullhypothese fälschlicherweise abzulehnen ist genau die Wahrscheinlichkeit für den Fehler 1. Art und ergibt sich somit als
Wahrscheinlichkeit für eine irrtümliche Ablehnung der Nullhypothese berechnen
Die Wahrscheinlichkeit dafür, die Nullhypothese fälschlicherweise abzulehnen ist genau die Wahrscheinlichkeit für den Fehler 1. Art und ergibt sich somit als  .
.
In der Tabelle zur kumulierten Binomialverteilung findest du den Wert .
Die Wahrscheinlichkeit dafür, die Nullhypothese fälschlicherweise abzulehnen, beträgt ca.
.
Die Wahrscheinlichkeit dafür, die Nullhypothese fälschlicherweise abzulehnen, beträgt ca.  .
.
In der Tabelle zur kumulierten Binomialverteilung findest du den Wert
b) (5)
 Ermitteln der gesamten Irrtumswahrscheinlichkeit
Die gesamte Irrtumswahrscheinlichkeit setzt sich zusammen aus den beiden Wahrscheinlichkeiten aus dem vorherigen Aufgabenteil,
Ermitteln der gesamten Irrtumswahrscheinlichkeit
Die gesamte Irrtumswahrscheinlichkeit setzt sich zusammen aus den beiden Wahrscheinlichkeiten aus dem vorherigen Aufgabenteil,  und
und  , die den Wahrscheinlichkeiten für den Fehler 1. Art und für den Fehler 2. Art entsprechen. Allerdings muss dabei berücksichtigt werden, dass die Palette zufällig aus den 10 vorhandenen Paletten ausgewählt wurde. Der Fehler 1. Art kann nur begangen werden, wenn eine Palette mit B-Fliesen ausgewählt wurde und der Fehler 2. Art kann nur begangen werden, wenn eine Palette mit A-Fliesen ausgewählt wurde. Es handelt sich hier also um ein zweistufiges Zufallsexperiment. Du musst also die entsprechenden Wahrscheinlichkeiten für eine Palette mit A-Fliesen und für eine Palette mit B-Fliesen berücksichtigen, insgesamt ergibt sich dann mit den beiden Pfadregeln die folgende Wahrscheinlichkeit:
, die den Wahrscheinlichkeiten für den Fehler 1. Art und für den Fehler 2. Art entsprechen. Allerdings muss dabei berücksichtigt werden, dass die Palette zufällig aus den 10 vorhandenen Paletten ausgewählt wurde. Der Fehler 1. Art kann nur begangen werden, wenn eine Palette mit B-Fliesen ausgewählt wurde und der Fehler 2. Art kann nur begangen werden, wenn eine Palette mit A-Fliesen ausgewählt wurde. Es handelt sich hier also um ein zweistufiges Zufallsexperiment. Du musst also die entsprechenden Wahrscheinlichkeiten für eine Palette mit A-Fliesen und für eine Palette mit B-Fliesen berücksichtigen, insgesamt ergibt sich dann mit den beiden Pfadregeln die folgende Wahrscheinlichkeit:
 Die gesamte Irrtumswahrscheinlichkeit beträgt
Die gesamte Irrtumswahrscheinlichkeit beträgt  .
.
c) (1)
 Graphische Darstellung
Du sollst hier die neue Situation, die sich durch die Einführung der Testmaschine ergeben hat, graphisch darstellen. Für eine übersichtlichere Darstellung kannst du zunächst folgende oder ähnliche Bezeichnungen einführen:
Graphische Darstellung
Du sollst hier die neue Situation, die sich durch die Einführung der Testmaschine ergeben hat, graphisch darstellen. Für eine übersichtlichere Darstellung kannst du zunächst folgende oder ähnliche Bezeichnungen einführen:
 Lösungsweg A: Baumdiagramm
Um die Situation mit Hilfe eines Baumdiagramms darzustellen, überlege dir zunächst, wie viele Stufen hier vorliegen und gehe dann in jeder Stufe jede Möglichkeit durch.
Die erste Stufe ist die Produktion der Fliesen von Maschine A. Hier wird jede Fliese zur „1. Wahl“-Fliese oder „2. Wahl“-Fliese. Die Wahrscheinlichkeiten sind dementsprechend die Wahrscheinlichkeit dafür, dass Maschine A eine „1. Wahl“- bzw. „2. Wahl“-Fliese produziert.
Die nächste Stufe ist dann die Sortierung der Testmaschine. Diese hängt von der ersten Stufe ab. Die Wahrscheinlichkeiten in dieser Stufe kannst du der Aufgabenstellung entnehmen bzw. mit Hilfe des Gegenereignisses berechnen. Insgesamt besteht das Zufallsexperiment hier also aus 2 Stufen und das Baumdiagramm ergibt sich nun wie folgt:
Lösungsweg A: Baumdiagramm
Um die Situation mit Hilfe eines Baumdiagramms darzustellen, überlege dir zunächst, wie viele Stufen hier vorliegen und gehe dann in jeder Stufe jede Möglichkeit durch.
Die erste Stufe ist die Produktion der Fliesen von Maschine A. Hier wird jede Fliese zur „1. Wahl“-Fliese oder „2. Wahl“-Fliese. Die Wahrscheinlichkeiten sind dementsprechend die Wahrscheinlichkeit dafür, dass Maschine A eine „1. Wahl“- bzw. „2. Wahl“-Fliese produziert.
Die nächste Stufe ist dann die Sortierung der Testmaschine. Diese hängt von der ersten Stufe ab. Die Wahrscheinlichkeiten in dieser Stufe kannst du der Aufgabenstellung entnehmen bzw. mit Hilfe des Gegenereignisses berechnen. Insgesamt besteht das Zufallsexperiment hier also aus 2 Stufen und das Baumdiagramm ergibt sich nun wie folgt:

 Lösungsweg B: Vierfeldertafel
Beginne bei der Vierfeldertafel damit die Wahrscheinlichkeiten einzutragen, die du direkt der Aufgabenstellung entnehmen kannst. Fülle anschließend die Vierfeldertafel auf, indem du aus den bekannten Wahrscheinlichkeiten die übrigen Wahrscheinlichkeiten bestimmst. Beachte dabei, dass sich der Eintrag einer Vierfeldertafel in der Spalte zu Ereignis
Lösungsweg B: Vierfeldertafel
Beginne bei der Vierfeldertafel damit die Wahrscheinlichkeiten einzutragen, die du direkt der Aufgabenstellung entnehmen kannst. Fülle anschließend die Vierfeldertafel auf, indem du aus den bekannten Wahrscheinlichkeiten die übrigen Wahrscheinlichkeiten bestimmst. Beachte dabei, dass sich der Eintrag einer Vierfeldertafel in der Spalte zu Ereignis  und in der Zeile zu Ereignis
und in der Zeile zu Ereignis  aus
aus  ergibt. Es gilt
ergibt. Es gilt
 Es geht hier also um bedingte Wahrscheinlichkeiten. Daraus kannst du folgende Wahrscheinlichkeiten mit Hilfe des Gegenereignisses berechnen:
Es geht hier also um bedingte Wahrscheinlichkeiten. Daraus kannst du folgende Wahrscheinlichkeiten mit Hilfe des Gegenereignisses berechnen:
 und
und  Damit ergibt sich nun folgendes:
Damit ergibt sich nun folgendes:
 Wahrscheinlichkeit berechnen
Du sollst hier die Wahrscheinlichkeit dafür berechnen, dass eine zufällig ausgewählte Fliese als 1. Wahl eingestuft wird. Gesucht ist also
Wahrscheinlichkeit berechnen
Du sollst hier die Wahrscheinlichkeit dafür berechnen, dass eine zufällig ausgewählte Fliese als 1. Wahl eingestuft wird. Gesucht ist also  . Je nachdem welchen Lösungsweg du im letzten Aufgabenteil gewählt hast, unterscheidet sich auch hier der Lösungsweg.
. Je nachdem welchen Lösungsweg du im letzten Aufgabenteil gewählt hast, unterscheidet sich auch hier der Lösungsweg.
 Lösungsweg A: Baumdiagramm
Die gesuchte Wahrscheinlichkeit ergibt sich hier mit den Pfadregeln:
Lösungsweg A: Baumdiagramm
Die gesuchte Wahrscheinlichkeit ergibt sich hier mit den Pfadregeln:
![\(\begin{array}[t]{rll}
P(T_1)&=&P(T_1\mid W_1)\cdot P(W_1) + P(T_1\mid W_2)\cdot W_2 \quad \scriptsize \\[5pt]
&=&0,9\cdot 0,95+ 0,1\cdot 0,2 \quad \scriptsize \\[5pt]
&=&0,875 \quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/da25ef292b6f1e207ea5529b89c1acef3aaa6b2f1be4a48657d701efbc6609cf?color=5a5a5a) Mit einer Wahrscheinlichkeit von
Mit einer Wahrscheinlichkeit von  wird eine zufällig ausgewählte Fliese aus Maschine A von der Testmaschine als 1. Wahl eingestuft und somit nicht aussortiert.
wird eine zufällig ausgewählte Fliese aus Maschine A von der Testmaschine als 1. Wahl eingestuft und somit nicht aussortiert.
 Lösungsweg B: Vierfeldertafel
Mit Hilfe der Vierfeldertafel, kannst du die gesuchte Wahrscheinlichkeit direkt ablesen:
Lösungsweg B: Vierfeldertafel
Mit Hilfe der Vierfeldertafel, kannst du die gesuchte Wahrscheinlichkeit direkt ablesen:
 Mit einer Wahrscheinlichkeit von
Mit einer Wahrscheinlichkeit von  wird eine zufällig ausgewählte Fliese aus Maschine A von der Testmaschine als 1. Wahl eingestuft und somit nicht aussortiert.
wird eine zufällig ausgewählte Fliese aus Maschine A von der Testmaschine als 1. Wahl eingestuft und somit nicht aussortiert.
: Die vorliegende Fliese ist 1. Wahl
: Die vorliegende Fliese ist 2. Wahl
: Die vorliegende Fliese wird von der Testmaschine als 1. Wahl bezeichnet
: Die vorliegende Fliese wird von der Testmaschine als 2. Wahl bezeichnet

| Summe | |||
|---|---|---|---|
| Summe |
c) (2)
 Wahrscheinlichkeit berechnen
Hier sollst du nun die Wahrscheinlichkeit dafür berechnen, dass eine Fliese eine „2. Wahl“-Fliese ist unter der Bedingung, dass sie von der Maschine nicht aussortiert wurde, also als 1. Wahl eingestuft wurde. Gesucht ist also
Wahrscheinlichkeit berechnen
Hier sollst du nun die Wahrscheinlichkeit dafür berechnen, dass eine Fliese eine „2. Wahl“-Fliese ist unter der Bedingung, dass sie von der Maschine nicht aussortiert wurde, also als 1. Wahl eingestuft wurde. Gesucht ist also  . Du kannst hier den Satz von Bayes verwenden:
. Du kannst hier den Satz von Bayes verwenden:
 Damit ergibt sich dann:
Damit ergibt sich dann:
![\(\begin{array}[t]{rll}
P(W_2 \mid T_1) &=& \dfrac{P(T_1\mid W_2)\cdot P(W_2)}{P(T_1)} \quad \scriptsize \\[5pt]
&=& \dfrac{0,1\cdot 0,2}{0,875}\quad \scriptsize \\[5pt]
&\approx&0,0229 \quad \scriptsize \\[5pt]
&=&2,29\,\% \quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/68a81c39bb3e855651068f46c4b8983af70a9d7c526315941115738dfbaa8b97?color=5a5a5a) Mit einer Wahrscheinlichkeit von ca.
Mit einer Wahrscheinlichkeit von ca.  ist eine nicht aussortierte Fliese eine „2. Wahl“-Fliese.
ist eine nicht aussortierte Fliese eine „2. Wahl“-Fliese.
c) (3)
 Aussortierwahrscheinlichkeit berechnen
Gesucht ist hier
Aussortierwahrscheinlichkeit berechnen
Gesucht ist hier  , sodass die Wahrscheinlichkeit
, sodass die Wahrscheinlichkeit  kleiner als
kleiner als  ist. Mit der Gleichung aus der letzten Aufgabe ergibt sich folgendes:
ist. Mit der Gleichung aus der letzten Aufgabe ergibt sich folgendes:
![\(\begin{array}[t]{rll}
P(W_2\mid T_1)& \lt &0,01 \quad \scriptsize \\[5pt]
\dfrac{P(T_1\mid W_2)\cdot P(W_2)}{P(T_1)} & \lt &0,01 \quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/46b3639eed4ee0853d90ebe7b2b99b62f4d12118946515ca8a7a526222b5dc15?color=5a5a5a) Bestimme nun die einzelnen Bestandteile dieser Ungleichung für allgemeines
Bestimme nun die einzelnen Bestandteile dieser Ungleichung für allgemeines  , um anschließend einsetzen und nach
, um anschließend einsetzen und nach  lösen zu können.
Es gilt
lösen zu können.
Es gilt  und damit
und damit  . Wegen
. Wegen  gilt nun:
gilt nun:
 Einsetzen ergibt nun:
Einsetzen ergibt nun:
![\(\begin{array}[t]{rll}
\dfrac{P(T_1\mid W_2)\cdot P(W_2)}{P(T_1)} &\lt & 0,01\quad \scriptsize \\[5pt]
\dfrac{(1-w)\cdot 0,1}{ 0,855 + (1-w)\cdot 0,1}&\lt &0,01 &\quad \scriptsize \mid\;\cdot (0,855 + (1-w)\cdot 0,1) \\[5pt]
(1-w)\cdot 0,1&\lt & 0,00855 + (1-w)\cdot 0,001 &\quad \scriptsize \mid\; - 0,001(1-w) \\[5pt]
0,099(1-w) &\lt & 0,00855 &\quad \scriptsize \mid\; : 0,099\\[5pt]
1-w&\lt & \frac{19}{220}&\quad \scriptsize \mid\; +w \\[5pt]
1 &\lt & \frac{19}{220} +w&\quad \scriptsize \mid\;- \frac{19}{220} \\[5pt]
\frac{201}{220}&\lt &w &\quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/0aa1912ead17e05607d2d0421ae7b4c8474193473f09010ddbd6be3cbf4c2a7b?color=5a5a5a) Insgesamt muss also
Insgesamt muss also  gelten, damit die Wahrscheinlichkeit für eine fälschlicherweise nicht aussortierte Fliese 2. Wahl unter
gelten, damit die Wahrscheinlichkeit für eine fälschlicherweise nicht aussortierte Fliese 2. Wahl unter  sinkt.
sinkt.