Analysis 1
Aufgabe 1
Im Oktober des Jahres 2000 wurden auf einer Waldfläche Fichten gepflanzt. Alle Fichten hatten zum Zeitpunkt der Pflanzung eine Höhe vonDiese Wachstumsrate wird für
Die Abbildung zeigt den Graphen von
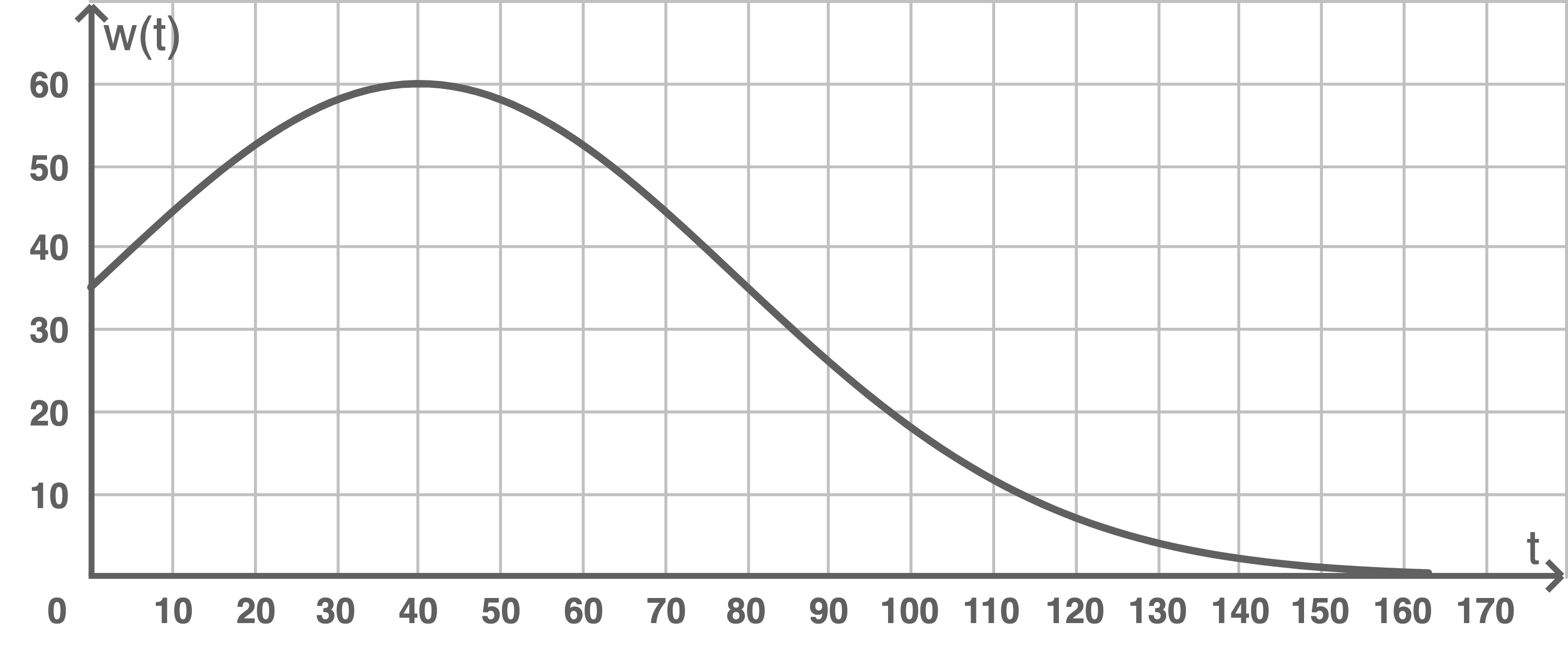
a)
Bestätige rechnerisch, dass die Wachstumsrate im Jahr 2040 am größten ist.
Bestimme rechnerisch den Zeitraum in Jahren, in dem die Fichten mehr als wachsen.
wachsen.
Bestimme rechnerisch den Zeitraum in Jahren, in dem die Fichten mehr als
(4 Punkte)
b)
Begründe die folgende Aussage:
Innerhalb der ersten 80 Jahre nach der Pflanzung sind für zwei beliebige Zeitpunkte, die den gleichen zeitlichen Abstand vom Oktober des Jahres 2040 haben, die zugehörigen Wachstumsraten gleich groß.
Innerhalb der ersten 80 Jahre nach der Pflanzung sind für zwei beliebige Zeitpunkte, die den gleichen zeitlichen Abstand vom Oktober des Jahres 2040 haben, die zugehörigen Wachstumsraten gleich groß.
(2 Punkte)
c)
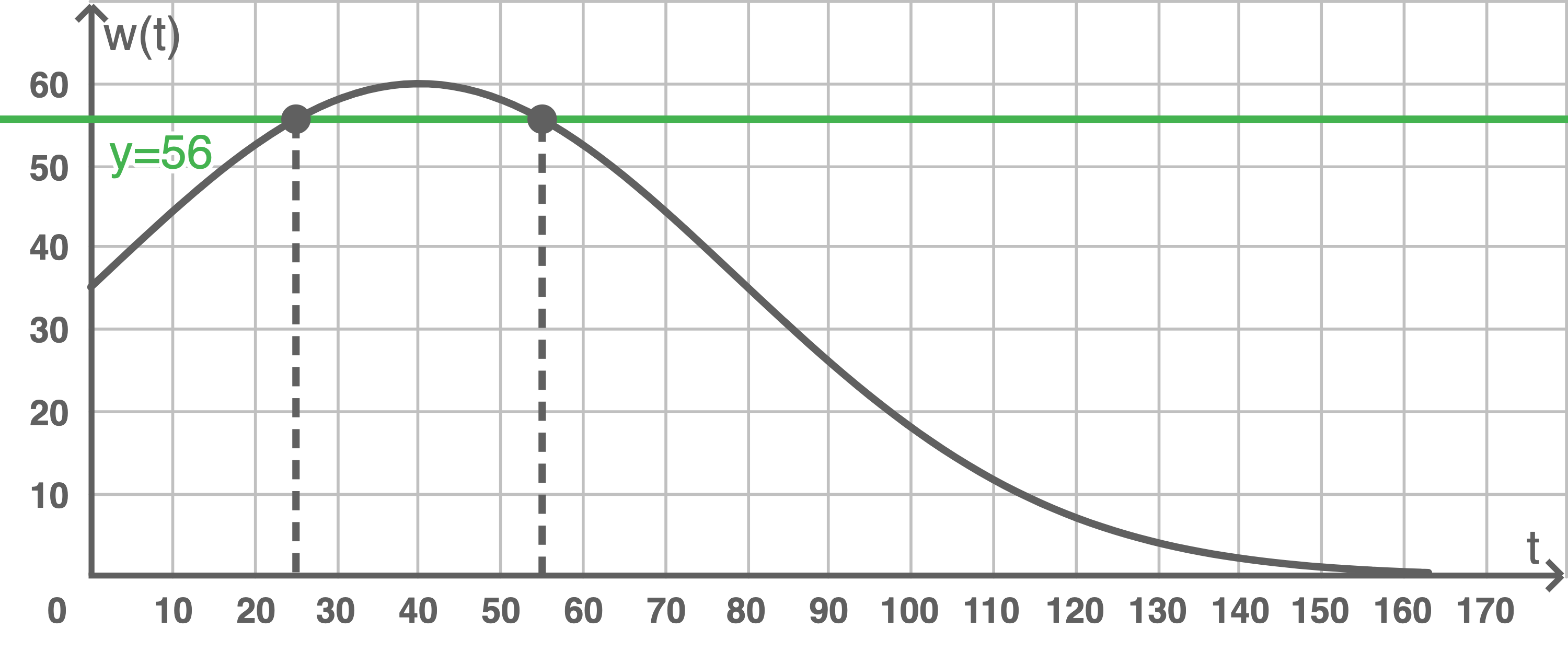
Zu einer bestimmten Wachstumsrate ist der Zeitraum, in dem diese Wachstumsrate nicht unterschritten wird, genau 30 Jahre lang. Gib diesen Zeitraum an und bestimme den Wert der Wachstumsrate. Veranschauliche dein Ergebnis in der obigen Abbildung.
(4 Punkte)
d)
Gib die Bedeutung des Terms
 im Sachzusammenhang an und begründe deine Angabe.
im Sachzusammenhang an und begründe deine Angabe.
(4 Punkte)
e)
Skizziere die Höhe der Fichten in Abhängigkeit von der Zeit beginnend mit dem Zeitpunkt der Pflanzung bis zum Jahr 2180.
Erläutere anhand von drei Argumenten den Verlauf des Graphen.
Erläutere anhand von drei Argumenten den Verlauf des Graphen.
(4 Punkte)
Aufgabe 2
In einem anderen Modell wird die Höhe der Fichten in Abhängigkeit von der Zeit mithilfe der inDabei ist
a)
Bestimme die Koordinaten von  .
.
 Kontrollergebnis: Die gerundeten Koordinaten des Wendepunktes sind
Kontrollergebnis: Die gerundeten Koordinaten des Wendepunktes sind 
(3 Punkte)
b)
Eine Zeitschrift von  enthält folgenden Textabschnitt:
Von unseren einheimischen Bäumen steht die Fichte hinsichtlich ihres Höhenwachstums obenan, und zwar mit 37 Zentimeter durchschnittlich im Jahre. Doch sind von Forstbeamten Ausnahmen beobachtet worden, in denen Fichten in einem Jahre bis zu 150 Zentimeter ihrer Länge zusetzten.
enthält folgenden Textabschnitt:
Von unseren einheimischen Bäumen steht die Fichte hinsichtlich ihres Höhenwachstums obenan, und zwar mit 37 Zentimeter durchschnittlich im Jahre. Doch sind von Forstbeamten Ausnahmen beobachtet worden, in denen Fichten in einem Jahre bis zu 150 Zentimeter ihrer Länge zusetzten.
(Quelle: Walther Kabel: Wachstumsgeschwindigkeit bei Pflanzen. In: Das Buch für Alle.
Jahrgang 1911, Heft 1, Union Deutsche Verlagsgesellschaft. Stuttgart 1911, S. 23.) Vergleiche die durch die Funktion bestimmte maximale Wachstumsgeschwindigkeit in Zusammenhang mit den Angaben dieses Textabschnitts.
bestimmte maximale Wachstumsgeschwindigkeit in Zusammenhang mit den Angaben dieses Textabschnitts.
Jahrgang 1911, Heft 1, Union Deutsche Verlagsgesellschaft. Stuttgart 1911, S. 23.) Vergleiche die durch die Funktion
(3 Punkte)
c)
Im betrachteten Modell lässt sich die zeitliche Entwicklung der Höhe der Fichten für die ersten 20 Jahre ab der Pflanzung näherungsweise durch die Funktion  mit
mit  beschreiben. Gegeben sind zudem die folgenden Funktionsterme:
beschreiben. Gegeben sind zudem die folgenden Funktionsterme:


 Begründe, dass der Graph von
Begründe, dass der Graph von  zum Graphen von
zum Graphen von  bezüglich des Punkts
bezüglich des Punkts  symmetrisch ist.
Gib die Bedeutung von
symmetrisch ist.
Gib die Bedeutung von  im Sachzusammenhang an.
im Sachzusammenhang an.
 Hinweis: Der Graph von
Hinweis: Der Graph von  ist symmetrisch bezüglich
ist symmetrisch bezüglich  und es gilt
und es gilt 
(5 Punkte)
Aufgabe 3
Um den Verkaufswert eines Baumstamms zu bestimmen, wird dessen Durchmesser in einer Höhe von
a)
Ein Fichtenstamm hat einen BHD von  . Sein Volumen vom Boden bis zu einer Höhe von
. Sein Volumen vom Boden bis zu einer Höhe von  beträgt
beträgt  Es soll davon ausgegangen werden, dass der Durchmesser des Stamms mit zunehmender Höhe linear abnimmt. Berechne den Durchmesser des Stamms in einer Höhe von
Es soll davon ausgegangen werden, dass der Durchmesser des Stamms mit zunehmender Höhe linear abnimmt. Berechne den Durchmesser des Stamms in einer Höhe von  .
.
(7 Punkte)
b)
Für BHD ab  kann der Verkaufspreis von Fichtenstämmen in Abhängigkeit vom BHD näherungsweise mithilfe einer quadratischen Funktion bestimmt werden. Der Tabelle kann für drei BHB der jeweilige Preis entnommen werden. Ermittle den Preis für einen Fichtenstamm mit einem BHD von
kann der Verkaufspreis von Fichtenstämmen in Abhängigkeit vom BHD näherungsweise mithilfe einer quadratischen Funktion bestimmt werden. Der Tabelle kann für drei BHB der jeweilige Preis entnommen werden. Ermittle den Preis für einen Fichtenstamm mit einem BHD von  .
.
(4 Punkte)
(40 Punkte)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung 1
a)
Zeitpunkt mit der größten Wachstumsrate
Gesucht wird das Maximum der Funktion im Bereich  Mit der Kettenregel folgt:
Mit der Kettenregel folgt:
![\(\begin{array}[t]{rll}
w](https://mathjax.schullv.de/2737e5f80f43efd860f4b4ed575e4ad577b37f5340ab98ad8f892da776732b35?color=5a5a5a) Mit der notwendigen Bedingung für Extremstellen folgt:
Mit der notwendigen Bedingung für Extremstellen folgt:
![\(\begin{array}[t]{rll}
w](https://mathjax.schullv.de/fa0d3c29eed465573fcd98b9b5d51522830dba3d471b67962ac500478884e041?color=5a5a5a) Da stets
Da stets  für alle
für alle  folgt mit dem Satz des Nullproduktes:
folgt mit dem Satz des Nullproduktes:
![\(\begin{array}[t]{rll}
\dfrac{t - 40}{25}&=& 0&\quad \scriptsize \mid\; \cdot 25 \\[5pt]
t - 40&=& 0& \quad \scriptsize \mid\; +40 \\[5pt]
t& =& 40
\end{array}\)](https://mathjax.schullv.de/5fb7900fcef8e8b7a296ab107be42b468d746a09941a6eeb4324eaa4ce4ade57?color=5a5a5a) Auf die Anwendung der hinreichende Bedingung für Extremstellen kann verzichtet werden, da aus der Aufgabenstellung und aus der Abbildung folgt, dass es sich um ein Maximum handelt.
Folglich ist die Wachstumsrate im Jahr 2040 am größten.
Zeitraum bestimmen
Auf die Anwendung der hinreichende Bedingung für Extremstellen kann verzichtet werden, da aus der Aufgabenstellung und aus der Abbildung folgt, dass es sich um ein Maximum handelt.
Folglich ist die Wachstumsrate im Jahr 2040 am größten.
Zeitraum bestimmen
![\(\begin{array}[t]{rll}
w(t)&\gt& 50 \\[5pt]
60 \cdot \mathrm e^{-\frac{1}{3000}\cdot (t-40)^2}&\gt& 50 &\quad \scriptsize \mid\; :60 \\[5pt]
\mathrm e^{-\frac{1}{3000}\cdot (t-40)^2} &\gt& \dfrac{5}{6} &\quad \scriptsize \mid\; \ln(\;)\\[5pt]
-\dfrac{1}{3000}\cdot (t-40)^2 &\gt& \ln \left(\dfrac{5}{6} \right) &\quad \scriptsize \mid\;\cdot (-3000) \\[5pt]
(t-40)^2 &\lt& 546,97 &\quad \scriptsize \mid\; \sqrt{\;} \\[5pt]
t-40&\lt& \pm 23,39 &\quad \scriptsize \mid\; +40
\end{array}\)](https://mathjax.schullv.de/52bfd2e3681dda9a8af80bf02b4d0e3cd57a87f8b2804a58e6f22ee9f1a239aa?color=5a5a5a) Daraus folgt
Daraus folgt  und
und  Für
Für  liefert
liefert  näherungsweise
näherungsweise  D.h. der Zeitraum, in dem die Fichten mehr als
D.h. der Zeitraum, in dem die Fichten mehr als  wachsen, entspricht circa den Jahren von 2017 bis einschließlich 2064.
wachsen, entspricht circa den Jahren von 2017 bis einschließlich 2064.
b)
Der Exponent der Exponentialfunktion  ist
ist  Dieser Term beschreibt eine nach unten geöffnete Parabel mit dem Scheitelpunkt
Dieser Term beschreibt eine nach unten geöffnete Parabel mit dem Scheitelpunkt  Diese Parabel verläuft achsensymmetrisch zur Geraden
Diese Parabel verläuft achsensymmetrisch zur Geraden  Für alle beliebigen Zeitpunkte
Für alle beliebigen Zeitpunkte  und
und  mit
mit  die den gleichen zeitlichen Abstand zum Zeitpunkt der größten Wachstumsrate
die den gleichen zeitlichen Abstand zum Zeitpunkt der größten Wachstumsrate  haben, ist also der Wert des Terms identisch und damit auch der Funktionswert von
haben, ist also der Wert des Terms identisch und damit auch der Funktionswert von  Für alle
Für alle  gilt
gilt  Die Wachstumsrate ist also für solche Zeitpunkte gleich.
Die Wachstumsrate ist also für solche Zeitpunkte gleich.
c)
Der gesuchte Zeitraum entspricht einem Wertepaar, welches sich im Intervall ![\([0;80]\)](https://mathjax.schullv.de/fff53c079acd87232df98ea62e23d85afae9fdf09f6750a96b4591a522432aca?color=5a5a5a) befinden muss. Da der Graph von
befinden muss. Da der Graph von  im Intervall
im Intervall ![\([0;80]\)](https://mathjax.schullv.de/fff53c079acd87232df98ea62e23d85afae9fdf09f6750a96b4591a522432aca?color=5a5a5a) parabelförmig und achsensymmetrisch zur Geraden
parabelförmig und achsensymmetrisch zur Geraden  verläuft (siehe Teilaufgabe b), ergibt sich der Zeitraum zu
verläuft (siehe Teilaufgabe b), ergibt sich der Zeitraum zu  Zeitraum: Oktober
Zeitraum: Oktober  bis einschließlich Oktober
bis einschließlich Oktober  Mit dem Taschenrechner ergibt sich
Mit dem Taschenrechner ergibt sich  d.h. die Wachstumsrate beträgt etwa
d.h. die Wachstumsrate beträgt etwa 

d)
Der Term gibt die Höhe der Fichten in Metern, 60 Jahre nach der Pflanzung, also im Oktober 2060 an.
50 ist die Anfangshöhe der Fichten zum Zeitpunkt der Pflanzung in Zentimetern. Der Wert des Integrals gibt die Änderung der Höhe innerhalb der ersten 60 Jahre nach der Pflanzung in Zentimetern an. Der Faktor  führt zu einem Wert in Metern.
führt zu einem Wert in Metern.
e)
Die Funktion für die Höhe der Fichte entspricht einer Stammfunktion von  Da die Fichte anfangs
Da die Fichte anfangs ![\(c=50 \; [\text{cm}]\)](https://mathjax.schullv.de/2d6d6fe4106524f11e31830126af6d5d84cb0c01339435d93bc5e31d18303183?color=5a5a5a) hoch ist, folgt der Graph der Funktion mit:
hoch ist, folgt der Graph der Funktion mit:
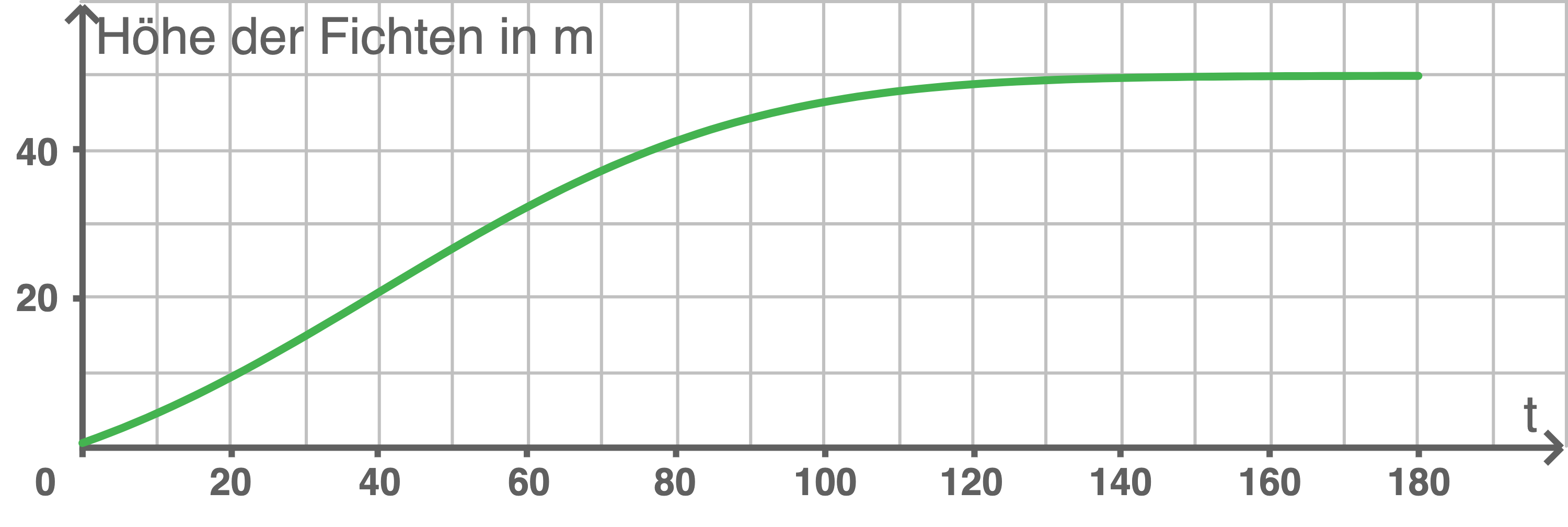 Drei mögliche Argumente sind:
Drei mögliche Argumente sind:

- Anfangswert bei
- Wendepunkt bei
- Schranke bei ca.
Lösung 2
a)
Mit dem Taschenrechner wird die erste Ableitungsfunktion graphisch dargestellt und auf Extremstellen untersucht.
Als Extremstelle ergibt sich  Mit
Mit  ergeben sich die Koordinaten des Wendepunktes mit
ergeben sich die Koordinaten des Wendepunktes mit  Alternativer Lösungsweg
Mit Hilfe des Taschenrechners lässt sich die zweite Ableitung von
Alternativer Lösungsweg
Mit Hilfe des Taschenrechners lässt sich die zweite Ableitung von  berechnen:
berechnen:
 Anwendung der notwendigen Bedingung für Wendestellen ergibt:
Anwendung der notwendigen Bedingung für Wendestellen ergibt:
![\(\begin{array}[t]{rll}
h](https://mathjax.schullv.de/e28d616072840d2d6536e7eb392904bbff6dd57087fd3d6a0cbb9ce8189768dd?color=5a5a5a) Mit dem solve-Befehl des Taschenrechners folgt
Mit dem solve-Befehl des Taschenrechners folgt  Auf die Anwendung der hinreichenden Bedingung für Wendestellen kann verzichtet werden, da aus der Aufgabenstellung folgt, dass eine Wendestelle existiert.
Auf die Anwendung der hinreichenden Bedingung für Wendestellen kann verzichtet werden, da aus der Aufgabenstellung folgt, dass eine Wendestelle existiert.
 Die Koordinaten des Wendepunkts des Graphen von
Die Koordinaten des Wendepunkts des Graphen von  lauten also
lauten also 
b)
Es gilt 
Die maximale Wachstumsgeschwindigkeit beträgt ca. ist im Sinne des Textes also als Ausnahmefall zu betrachten.
ist im Sinne des Textes also als Ausnahmefall zu betrachten.
Die maximale Wachstumsgeschwindigkeit beträgt ca.
c)
Der Graph von  ist gegenüber dem Graphen von
ist gegenüber dem Graphen von  gestreckt und entlang der negativen
gestreckt und entlang der negativen  -Achse verschoben.
-Achse verschoben.
Der Graph von ist zum Graphen von
ist zum Graphen von  punktsymmetrisch zum Ursprung.
punktsymmetrisch zum Ursprung.
Der Graph von ist zum Graphen von
ist zum Graphen von  gestaucht und entlang der positiven
gestaucht und entlang der positiven  -Achse verschoben. Außerdem ist der Graph von
-Achse verschoben. Außerdem ist der Graph von  zum Graphen von
zum Graphen von  symmetrisch bezüglich
symmetrisch bezüglich 
 beschreibt im Modell näherungsweise die zeitliche Entwicklung der Höhe der Fichten für den Zeitraum von etwa
beschreibt im Modell näherungsweise die zeitliche Entwicklung der Höhe der Fichten für den Zeitraum von etwa  bis etwa
bis etwa  Jahre nach der Pflanzung.
Jahre nach der Pflanzung.
Der Graph von
Der Graph von
Lösung 3
a)
Der Stamm lässt sich durch einen Körper darstellen, der durch Rotation des Graphen einer Funktion  um die
um die  -Achse entsteht.
-Achse entsteht.
Der Term von hat die Form
hat die Form 
Mit der Lösung der Gleichung für
für 
ergibt sich der Durchmesser in einer Höhe von
der Durchmesser in einer Höhe von  beträgt also etwa
beträgt also etwa 
Der Term von
Mit der Lösung der Gleichung
ergibt sich
b)
Es gilt:
 Mit den Werten aus der Tabelle folgt:
Mit den Werten aus der Tabelle folgt:
![\(\begin{array}[t]{rll}
p(10)&=& 0&\quad \scriptsize \\[5pt]
a\cdot 10^2 +b\cdot 10 +c&=& 0
\end{array}\)](https://mathjax.schullv.de/31e142e9e2090bc3c07934160686221d338f68cb2e18c416d405b4ee03a016db?color=5a5a5a)
![\(\begin{array}[t]{rll}
p(40)&=& 100 &\quad \scriptsize \\[5pt]
a\cdot 40^2 +b\cdot 40 +c&=& 100
\end{array}\)](https://mathjax.schullv.de/491f9a7ebd2a997284c77f74340eb019cad087850dd6a6ea6e178772fc38d79b?color=5a5a5a)
![\(\begin{array}[t]{rll}
p(60) &=& 250 &\quad \scriptsize \\[5pt]
a\cdot 60^2 +b\cdot 60 +c&=& 250
\end{array}\)](https://mathjax.schullv.de/4e3fde0876578db42a4f28ef53b230f79d3439662627450e0ac49566656fd24f?color=5a5a5a) Dies führt auf das folgende LGS:
Dies führt auf das folgende LGS:
 Das LGS ist mit dem GTR zu lösen und dieser liefert
Das LGS ist mit dem GTR zu lösen und dieser liefert  und
und  Daraus folgt
Daraus folgt 
 d.h. der Preis beträgt etwa
d.h. der Preis beträgt etwa 