Vektorielle Geometrie
Betrachtet werden die Pyramiden  mit
mit  ,
,  ,
,  ,
,  und
und  mit
mit 
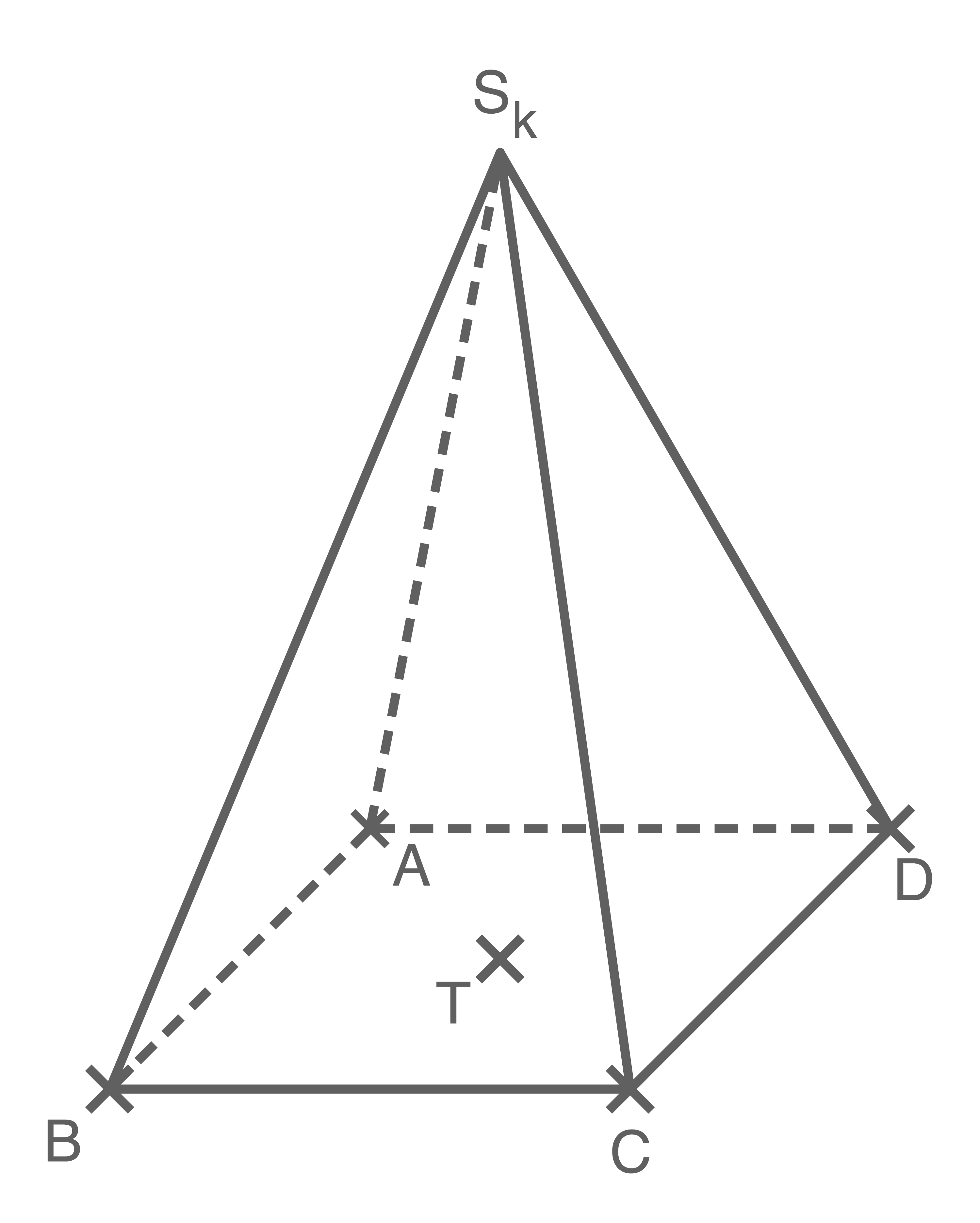
Die gemeinsame Grundfläche dieser Pyramiden ist quadratisch. Der Schnittpunkt der Diagonalen der Grundfläche
dieser Pyramiden ist quadratisch. Der Schnittpunkt der Diagonalen der Grundfläche  wird mit
wird mit  bezeichnet.
bezeichnet.
Die Abbildung zeigt beispielhaft eine dieser Pyramiden.
Die gemeinsame Grundfläche
Die Abbildung zeigt beispielhaft eine dieser Pyramiden.

a)
Berechne den Inhalt der Oberfläche der Pyramide 
(5 Punkte)
b)
Der Punkt  wird am Punkt
wird am Punkt  gespiegelt.
gespiegelt.
Gib die Koordinaten des Spiegelpunktes in Abhängigkeit von
in Abhängigkeit von  an.
an.
Berechne den Wert von so, dass
so, dass  zu seinem Spiegelpunkt den Abstand
zu seinem Spiegelpunkt den Abstand  hat.
hat.
Gib die Koordinaten des Spiegelpunktes
Berechne den Wert von
(4 Punkte)
c)
Die Seitenfläche  liegt in der Ebene
liegt in der Ebene  .
.
Bestimme eine Gleichung von in Koordinatenform.
in Koordinatenform.
[zur Kontrolle: ]
]
Bestimme eine Gleichung von
[zur Kontrolle:
(3 Punkte)
d)
Bestimme denjenigen Wert von  , für den die Seitenfläche
, für den die Seitenfläche  gegenüber der Grundfläche
gegenüber der Grundfläche  um einen Winkel der Größe
um einen Winkel der Größe  geneigt ist.
geneigt ist.
(4 Punkte)
e)
Untersuche, ob es einen Wert für  gibt, sodass das Dreieck
gibt, sodass das Dreieck  rechtwinklig ist.
rechtwinklig ist.
(3 Punkte)
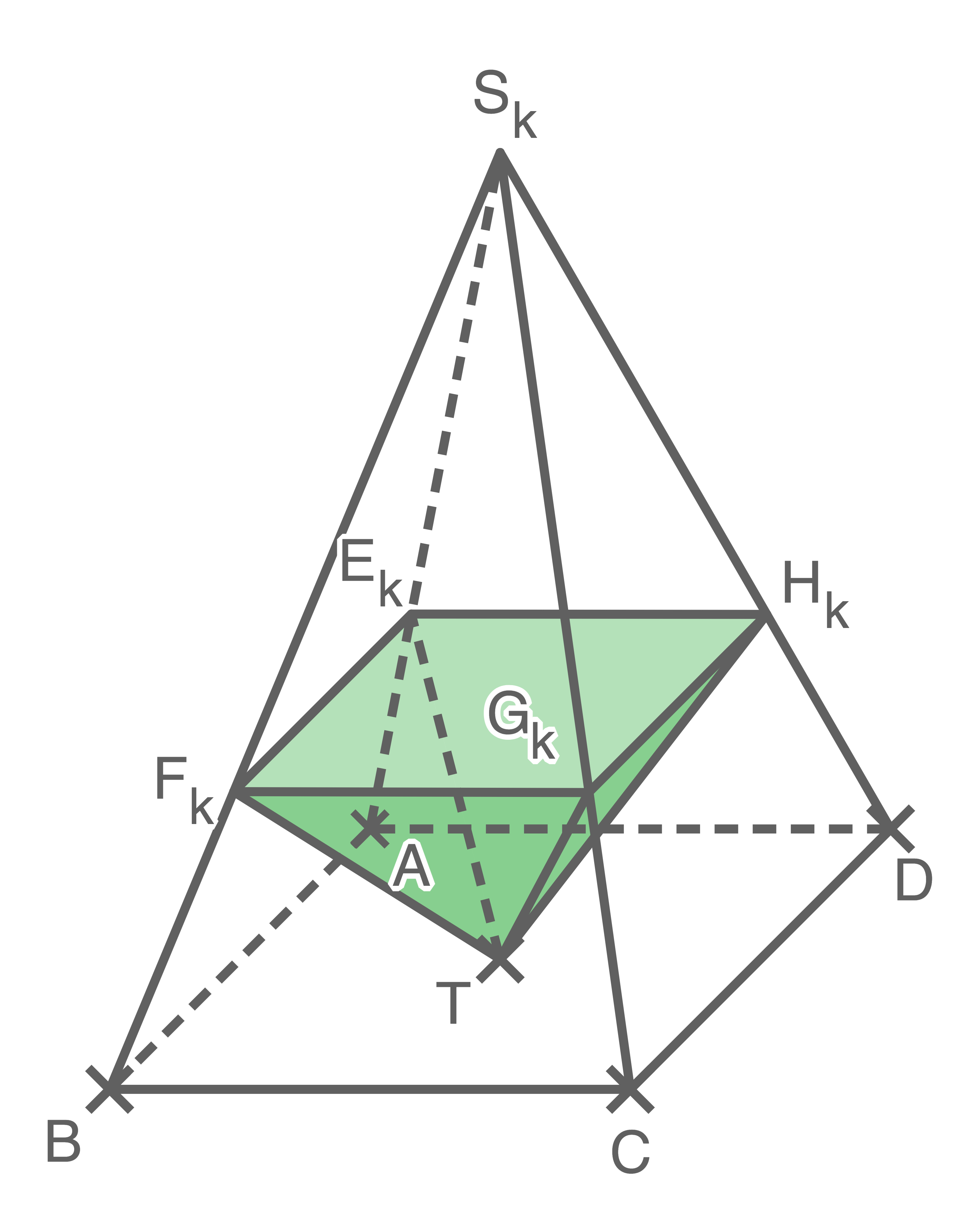
Die Ebene mit der Gleichung  schneidet die vier vom Punkt
schneidet die vier vom Punkt  ausgehenden Kanten der Pyramide
ausgehenden Kanten der Pyramide  in den Punkten
in den Punkten  ,
,  ,
,  und
und 

f)
Bestimme die  - und die
- und die  -Koordinate von
-Koordinate von  .
.
(2 Punkte)
g)
Bestimme diejenigen Werte von  , für die das Verhältnis des Volumens der Pyramide
, für die das Verhältnis des Volumens der Pyramide  zum Volumen der Pyramide
zum Volumen der Pyramide  beträgt.
beträgt.
(4 Punkte)
(25 Punkte)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
1. Schritt: Flächeninhalt der Grundfläche berechnen
 ,
, ![\(\mid \overrightarrow{AB} \mid = 2\,[\text{LE}]\)](https://mathjax.schullv.de/7688a52529d0ed5a32a57cf3689d7bedb86eeb6ab70411a9e26e9cd2f99df718?color=5a5a5a)
Da die Grundfläche der Pyramide quadratisch ist, folgt:![\(G= a^2=\mid \overrightarrow{AB} \mid^2 =2^2 =4 \;\text{[FE]}\)](https://mathjax.schullv.de/3548b0148ff93bd385c4d964478bf04f4327bd5ee7199d5a8eb81aba77975e4d?color=5a5a5a) 2. Schritt: Flächeninhalt einer Seitenfläche berechnen
Für den Inhalt der Seitenflächen gilt:
2. Schritt: Flächeninhalt einer Seitenfläche berechnen
Für den Inhalt der Seitenflächen gilt:  Die Koordinaten des Mittelpunkts der Strecke
Die Koordinaten des Mittelpunkts der Strecke  lassen sich aus den Koordinaten von
lassen sich aus den Koordinaten von  und
und  bestimmen:
bestimmen:
 Damit folgt:
Damit folgt:



![\(=\sqrt{1+k^2}\; \text{[LE]}.\)](https://mathjax.schullv.de/7e9a9bf0e01cac91092786ee75c6e1a792f18f006b1396b3cd052d385ebbdb70?color=5a5a5a) Der Flächeninhalt der Seitenfläche
Der Flächeninhalt der Seitenfläche  ergibt sich mit
ergibt sich mit 
![\(=\dfrac{1}{2} \cdot 2 \cdot \sqrt{1+k^2} \;\text{[FE]}.\)](https://mathjax.schullv.de/331f2b989ec736aefccd041c8455bc1fc4317a282036ac69ace4e1bcc8a5f3de?color=5a5a5a) 3. Schritt: Oberflächeninhalt berechnen
3. Schritt: Oberflächeninhalt berechnen
![\(\begin{array}[t]{rll}
0_P&=& G+ 4\cdot S \\[5pt]
&=& 4 +4 \cdot \dfrac{1}{2} \cdot 2 \cdot \sqrt{1+k^2} \\[5pt]
&=& 4+ 4\cdot \sqrt{1+k^2} \;\text{[FE]}
\end{array}\)](https://mathjax.schullv.de/41883f378441fa85507ef75e9153ffd3b25d83078eae81781df1a06df025ee09?color=5a5a5a)
Da die Grundfläche der Pyramide quadratisch ist, folgt:
b)
Koordinaten des Spiegelpunktes

 Die Koordinaten des Spiegelpunktes sind gegeben durch
Die Koordinaten des Spiegelpunktes sind gegeben durch  Wert von
Wert von  berechnen
berechnen


 Daraus folgt:
Daraus folgt:
![\(\begin{array}[t]{rll}
\mid \overrightarrow{S_kS](https://mathjax.schullv.de/e4175cac85443248b02b201937e092b7619e358e4b7f11ddaf0e0f7abf885d1c?color=5a5a5a)
c)
d)
Ein Normalenvektor der  -Ebene ist
-Ebene ist  Es muss gelten:
Es muss gelten:




 Damit folgt:
Damit folgt:
![\(\begin{array}[t]{rll}
\dfrac{1}{2}&=& \dfrac{1}{\sqrt{k^2+1}}&\quad \scriptsize \mid\;\cdot2\cdot\sqrt{k^2+1} \\[5pt]
\sqrt{k^2+1} &=& 2 &\quad \scriptsize \mid\;(\;)^2 \\[5pt]
k^2+1 &=& 4 &\quad \scriptsize \mid\;-1 \\[5pt]
k^2 &=& 3 &\quad \scriptsize \mid\;\sqrt{\;} \\[5pt]
k&=& \pm \sqrt{3}
\end{array}\)](https://mathjax.schullv.de/b4da707bf83d94b7d41184c824547657f935d49119de1b30d2f3d7d2c8d51cde?color=5a5a5a) Da
Da  ist der Wert mit
ist der Wert mit  bestimmt.
bestimmt.
e)
Das Dreieck  kann nur am Punkt
kann nur am Punkt  rechtwinklig sein. Dafür muss
rechtwinklig sein. Dafür muss  gelten.
gelten.




![\(\begin{array}[t]{rll}
\overrightarrow{BS_k} \circ \overrightarrow{DS_k} &=& 0 \\[5pt]
-2+k^2&=& 0 &\quad \scriptsize \mid\;+2 \\[5pt]
k^2&=& 2 &\quad \scriptsize \mid\;\sqrt{\;}\\[5pt]
k&=& \pm \sqrt{2}
\end{array}\)](https://mathjax.schullv.de/748dfd5b499be63d817c7e86d34a74f49181de35c54ae28bb30001b80ce14fbd?color=5a5a5a) Da
Da  ist der Wert mit
ist der Wert mit  bestimmt.
bestimmt.
f)
Es gilt: 
 Für die
Für die  -Koordinate gilt
-Koordinate gilt  Daraus folgt
Daraus folgt  Für die
Für die  -Koordinate gilt
-Koordinate gilt  und somit
und somit  Für die
Für die  -Koordinate gilt
-Koordinate gilt  und somit
und somit  Die Koordinaten von
Die Koordinaten von  sind gegeben durch
sind gegeben durch 
g)
1. Schritt: Volumen der Pyramide  berechnen
Aus Teilaufgabe a) ist bekannt, dass für die Grundfläche gilt
berechnen
Aus Teilaufgabe a) ist bekannt, dass für die Grundfläche gilt ![\(G=4\;[\text{FE}].\)](https://mathjax.schullv.de/effa306b4103ec5c707d32e72286be2ff92f6aacce36f192783b8b47b4e2721f?color=5a5a5a) Die Höhe ist durch die
Die Höhe ist durch die  -Koordinate des Punktes
-Koordinate des Punktes  gegeben, also
gegeben, also ![\(h_1=k\,[\text{LE}].\)](https://mathjax.schullv.de/472efa22682cad41e0cba05f59072676f19687dbdb66e4ef49c9ba80b474c1fe?color=5a5a5a) Damit ist das Volumen von
Damit ist das Volumen von  gegeben durch
gegeben durch ![\(V_{ABCDS_k}=\dfrac{1}{3} \cdot 4\cdot k \;[\text{VE}]\)](https://mathjax.schullv.de/8ddd5fe96e8069798e16f72f9fdb4b5b517d3c143807f33bc564d0d508bea8c3?color=5a5a5a) 2. Schritt: Volumen der Pyramide
2. Schritt: Volumen der Pyramide  bestimmen
Die Koordinaten von
bestimmen
Die Koordinaten von  lassen sich analog zu den Koordinaten von
lassen sich analog zu den Koordinaten von  aus Aufgabenteil f) berechnen und sind gegeben durch
aus Aufgabenteil f) berechnen und sind gegeben durch 

![\(= \,\bigg \vert \, \dfrac{2}{k}-2 \,\bigg \vert \, \,[\text{LE}]\)](https://mathjax.schullv.de/1aae1b83f23e39bc086c889521eeaa6335e19a536f84ba59874ef7e3bd93fd6f?color=5a5a5a) Die Höhe von
Die Höhe von  ist gegeben durch
ist gegeben durch ![\(h_2=1\,\text{[LE]}.\)](https://mathjax.schullv.de/42cd871bfb255808096e5c165de03a99ed11401e96bce9b1ba70551c3ceb3109?color=5a5a5a) Das Volumen der Pyramide
Das Volumen der Pyramide  beträgt damit
beträgt damit ![\(V_{E_kF_kG_kH_kT}=\dfrac{1}{3} \cdot \left(\dfrac{2}{k}-2 \right)^2 \;\text{[VE]}.\)](https://mathjax.schullv.de/3c13e406c2ba68e001c11d7285079c7e486f1833c0846cc3028be0ee24e3dd1c?color=5a5a5a) 3. Schritt: Volumen der Pyramiden ins Verhältnis setzen
3. Schritt: Volumen der Pyramiden ins Verhältnis setzen
![\(\begin{array}[t]{rll}
\dfrac{\dfrac{1}{3} \cdot \left(\dfrac{2}{k}-2 \right)^2}{\dfrac{4}{3}\cdot k}&=&\dfrac{1}{8} &\quad \scriptsize \mid\;\cdot \dfrac{4}{3} \cdot k\cdot 3\\[5pt]
\left(\dfrac{2}{k}-2 \right)^2&=&\dfrac{k}{2} &\quad \scriptsize \mid\; -\dfrac{k}{2} \\[5pt]
\left(\dfrac{2}{k}-2 \right)^2-\dfrac{k}{2}&=& 0
\end{array}\)](https://mathjax.schullv.de/bec9d19772cc4cf8a334a76c18187561d98e4884034b5f37035c353f6ff632de?color=5a5a5a) Die Lösungen dieser Gleichung ergeben sich mit dem solve-Befehl des Taschenrechners zu
Die Lösungen dieser Gleichung ergeben sich mit dem solve-Befehl des Taschenrechners zu  und
und 