Aufgabe 5

Die Abbildung zeigt modellhaft den Längsschnitt einer dreiteiligen Brücke aus Holz für eine Spielzeugeisenbahn. Die Züge können sowohl über die Brücke fahren als auch darunter hindurch.

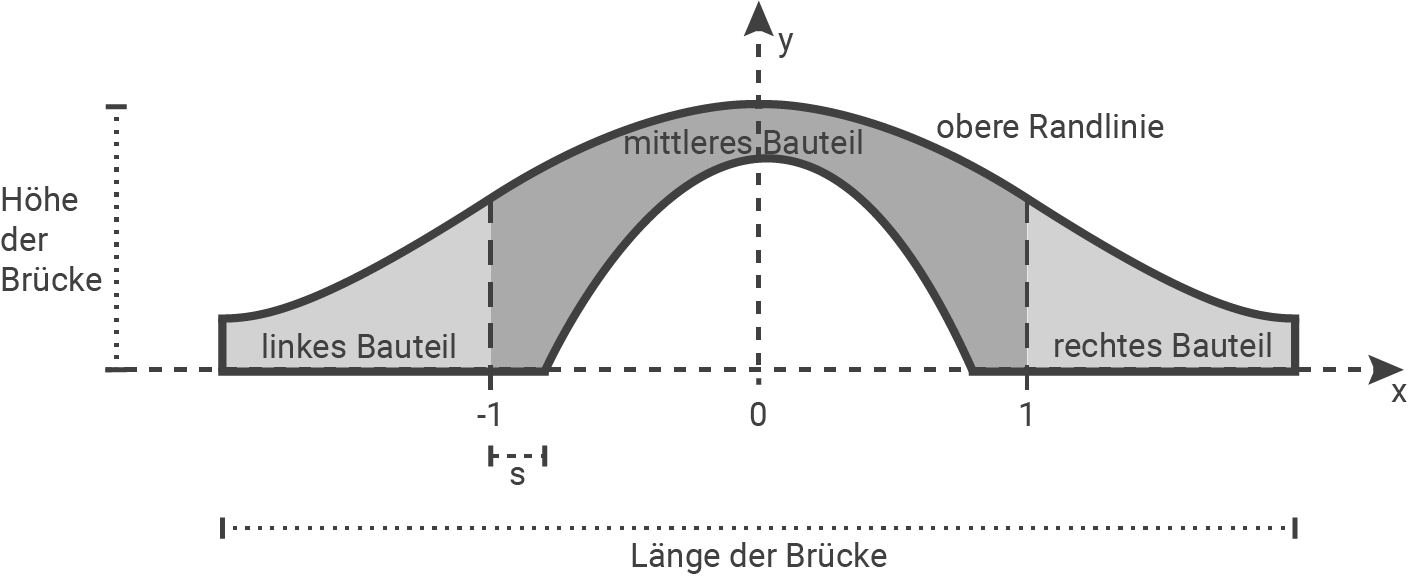Diagramm einer Brücke mit Bauteilen und Höhenangaben.

Abbildung

Die obere Randlinie des Längsschnitts der Brücke kann mithilfe des achsensymmetrischen Graphen der in $\mathbb{R}$ definierten Funktion $f$ mit $f(x)= \dfrac{1}{20}x^4- \dfrac{2}{5}x^2+1$ beschrieben werden. Dabei werden die Endpunkte dieser Randlinie durch die beiden Tiefpunkte des Graphen von $f$ dargestellt. Im verwendeten Koordinatensystem beschreibt die $x$ -Achse die Horizontale; eine Längeneinheit entspricht einem Dezimeter in der Realität.

Bestimme rechnerisch die Höhe und die Länge der Brücke.
[Kontrolllösung: Ein Tiefpunkt des Graphen von $f$ hat die $x$ -Koordinate $2.$ ]

(5 Punkte)

Betrachtet wird derjenige Punkt der oberen Randlinie, der sich am Übergang vom mittleren zum rechten Bauteil befindet. Prüfe, ob dieser Punkt auf halber Höhe zwischen dem höchsten Punkt der oberen Randlinie und deren rechtem Endpunkt liegt.

(3 Punkte)

Bestimme die größte Steigung der Brücke, die beim Überfahren zu überwinden ist.

(2 Punkte)

Der parabelförmige Teil der unteren Randlinie des Längsschnitts der Brücke kann mithilfe des Graphen einer in $\mathbb{R}$ definierten Funktion $q_a$ mit $q_a(x)=0,8-a \cdot x^2$ und $a \in \mathbb{R}$ , $a\gt 0$ , beschrieben werden.

In der Abbildung ist die Länge einer der beiden Bodenflächen des mittleren Bauteils mit $s$ bezeichnet. Bestimme alle Werte von $a,$ die für diese Länge mindestens $0,1 \;\text{dm}$ liefern.

(4 Punkte)

Begründe im Sachzusammenhang, dass für die Beschreibung der unteren Randlinie beliebig große Werte von $a$ nicht infrage kommen.

(2 Punkte)

Für die Brücke gilt $a=1,25.$ Die drei Bauteile der Brücke werden aus massivem Holz hergestellt; $1 \,\text{dm}^3$ des Holzes hat eine Masse von 800 Gramm. Die Brücke ist $0,4 \; \text{dm}$ breit. Ermittle die Masse des mittleren Bauteils.

(5 Punkte)

Während der Planung der Brückenform kamen zur Beschreibung der oberen Randlinie für das linke Bauteil eine Funktion $g_l$ und für das rechte Bauteil eine Funktion $g_r$ infrage. Auch bei der Verwendung dieser Funktionen wäre die obere Randlinie achsensymmetrisch gewesen.

Entscheide jeweils begründet, welche der folgenden Eigenschaften auf die Funktion $g_l$ und $g_r$ zutreffen.

(1)

$-g_l(x)=g_r(-x)$ für $-2\leq x \leq -1$

(2)

$g_l(x-1)=g_r(-x+1)$ für $-1\leq x\leq 0$

(4 Punkte)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Höhe der Brücke bestimmen

$f(0) =1$

Die Höhe der Brücke entspricht $1 \;\text{dm}.$

Länge der Brücke bestimmen

Um die Länge der Brücke zu bestimmen, müssen die $x$ -Koordinaten der Tiefpunkte bestimmt werden.

1. Schritt: Ableitungen bilden

$\(f$

2. Schritt: Notwendige Bedingung für Extremstellen anwenden

$\(\begin{array}[t]{rll} f$

Mit dem Satz vom Nullprodukt folgt $x_1=0$ oder $\dfrac{1}{5}x^2 - \dfrac{4}{5}=0.$

$\begin{array}[t]{rll} \dfrac{1}{5} x^2 - \dfrac{4}{5}&=&0 &\quad \scriptsize \mid\; +\dfrac{4}{5}\\[5pt] \dfrac{1}{5}x^2 &=& \dfrac{4}{5} &\quad \scriptsize \mid\; :\dfrac{1}{5} \\[5pt] x^2&=&4 \end{array}$

Daraus folgen $x_2=2$ und $x_3=-2$ als weitere Extremstellen.

3. Schritt: Hinreichende Bedingung für Extremstellen anwenden

$\(f$

Die Tiefpunkte des Graphen von $f$ liegen also an den Stellen $x_2=2$ und $x_3=-2.$

Der Abstand der $x$ -Koordinaten der Tiefpunkte beträgt $4 \;\text{LE}$ und somit beträgt die Länge der Brücke $4 \;\text{dm}.$

Höhe des Punktes am Übergang
Der Abbildung kann entnommen werden, dass der Punkt der oberen Randlinie, der sich am Übergang vom mittleren zum rechten Bauteil befindet, an der Stelle $x=1$ liegt.

$\begin{array}[t]{rll} f(1) &=& \dfrac{1}{20} \cdot 1^4-\dfrac{2}{5}\cdot 1^2+1 & \quad \scriptsize \\[5pt] f(1) &=& \dfrac{13}{20}\\[5pt] f(1) &=& 0,65 \\[5pt] \end{array}$

Halbe Höhe bestimmen

$\dfrac{f(0)+f(2)}{2} = \dfrac{1+0,2}{2} =0,6$

$f(1)=0,65 \neq 0,6$

Somit befindet sich der Punkt der oberen Randlinie, der sich am Übergang vom mittleren zum rechten Bauteil befindet, nicht auf halber Höhe zwischen dem höchsten Punkt der oberen Randlinie und deren rechtem Endpunkt.

Die größte Steigung der Brücke entspricht dem Wert des Maximums der ersten Ableitung.

Mit dem Taschenrechner wird zunächst die erste Ableitung bestimmt und dann graphisch das Maximum ermittelt.

$\(f$

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ trace (calc) $\to$ 4: maximum

$\blacktriangleright$ Casio fx-CG

F5 (G-Solv) $\to$ F2: MAX

Der Hochpunkt vom Graphen von $\(f$ hat die Koordinaten $(-1,155 \mid 0,616).$

Die größte Steigung, die beim Fahren zu Überwinden ist, entspricht also $\(f$

Für den Fall, dass die Länge der Bodenfläche des mittleren Bauteils genau $0,1 \;\text{dm}$ beträgt, hat der Graph von $q_a$ eine Nullstelle bei $x=-0,9.$ Damit lässt sich der Wert für $a$ wie folgt berechnen:

$\begin{array}[t]{rll} q(-0,9) &= & 0 \\[5pt] 0,8-a\cdot (-0,9)^2&= & 0 \\[5pt] \end{array}$

Mit dem solve-Befehl des Taschenrechners ergibt sich $a= \dfrac{80}{81}$ $\approx 0,988.$

Für $a \in \mathbb R,$ $a \gt 0$ ist der Graph von $q_a$ eine nach unten geöffnete Parabel. Wenn der Wert von $a$ vergrößert wird, dann veringert sich der Abstand der Nullstellen und somit wird die Länge $s$ größer. Daraus folgt, dass die Länge $s$ für $a \geq 0,988$ mindestens $0,1 \;\text{dm}$ lang ist.

Je größer der Wert von $a$ ist, desto schmaler ist der Graph von $q$ und damit die Durchfahrt der Brücke. Wird der Wert von $a$ zu groß, so kann kein Zug mehr hindurchfahren.

Es gilt: $q_{1,25}= 0,8- 1,25\cdot x^2.$

1. Schritt: Schnittstelle der Parabel $q_{1,25}$ mit der $x$ -Achse bestimmen

$\begin{array}[t]{rll} q(x) &= & 0 & \quad \scriptsize \\[5pt] 0,8-1,25\cdot x^2 &= & 0 & \quad \scriptsize \\[5pt] \end{array}$

Mit dem solve-Befehl des GTRs folgt $x_1= -0,8$ und $x_2=0,8.$

2. Schritt: Flächeninhalt der Längsschnittfläche berechnen

Der Wert des Flächeninhalts der Längsschnittfläche des mittleren Bauteils kann mit dem folgenden Integral berechnet werden:

$A= \displaystyle\int_{-1}^{1}f(x)\;\mathrm dx -\displaystyle\int_{-0,8}^{0,8}q_{1,25}(x)\;\mathrm dx$

Der Wert des Integrals wird mit dem Taschenrechner berechnet.

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ trace (calc) $\to$ 7: $\int f(x)\;\mathrm dx$

$\blacktriangleright$ Casio fx-CG

F5 (G-Solv) $\to$ F6 $\to$ F3: $\int \;\mathrm dx$

Daraus folgt der Flächeninhalt der Seitenfläche mit $A=0,9 \,\text{dm}^2.$

3. Schritt: Masse berechnen

Mit dem Flächeninhalt der Längsschnittfläche des mittleren Bauteils, der Breite der Brücke und der Masse des Holzes pro Kubikdezimeter, folgt die Masse des mittleren Bauteils mit:

$0,9 \,\text{dm}^2 \cdot 0,4 \,\text{dm} \cdot \dfrac{800 \,\text{g}}{1 \,\text{dm}^3}=288 \,\text{g}$

(1)

$-g_l(x)=g_r(-x)$ für $-2 \leq x \leq -1$

Mit der Gleichung wird eine Punktsymmetrie zum Ursprung der Graphen von $g_l$ und $g_r$ in den Intervallen $[-2; -1]$ und $[1; 2]$ beschrieben. Da die Graphen aber nicht symmetrisch sind, ist die Aussage falsch.

(2)

$g_l(x-1)=g_r(-x+1)$ für $-1 \leq x \leq 0$

Mit der Gleichung wird eine Achsensymmetrie zur $y$ -Achse der Graphen von $g_l$ und $g_r$ in den Intervallen $[-2; -1]$ und $[1; 2]$ beschrieben. Das passt zur beschriebenen Bedingung für die obere Randlinie, deshalb ist die Eigenschaft richtig.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?