Aufgabe 5
Für ein Schwimmbad besitzen  Personen eine Jahreskarte. Für einen bestimmten Tag beschreibt die Zufallsgröße
Personen eine Jahreskarte. Für einen bestimmten Tag beschreibt die Zufallsgröße  die Anzahl der Jahreskartenbesitzer, die das Schwimmbad besuchen. Vereinfachend soll davon ausgegangen werden, dass
die Anzahl der Jahreskartenbesitzer, die das Schwimmbad besuchen. Vereinfachend soll davon ausgegangen werden, dass  binomialverteilt ist. Dabei beträgt die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Jahreskartenbesitzer an diesem Tag das Schwimmbad besucht,
binomialverteilt ist. Dabei beträgt die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Jahreskartenbesitzer an diesem Tag das Schwimmbad besucht, 
a)
(1)
Es gilt  Interpretiere diese Aussage im Sachzusammenhang.
Interpretiere diese Aussage im Sachzusammenhang.
(2)
Bestimme die Wahrscheinlichkeit dafür, dass mehr als  Jahreskartenbesitzer das Schwimmbad besuchen.
Jahreskartenbesitzer das Schwimmbad besuchen.
(3)
Bestimme die Wahrscheinlichkeit dafür, dass der Wert von  höchstens um eine halbe Standardabweichung vom Erwartungswert der Zufallsgröße abweicht.
höchstens um eine halbe Standardabweichung vom Erwartungswert der Zufallsgröße abweicht.
(4)
Bestimme die größte natürliche Zahl  für die die Wahrscheinlichkeit dafür, dass weniger als
für die die Wahrscheinlichkeit dafür, dass weniger als  Jahreskartenbesitzer das Schwimmbad besuchen, kleiner als
Jahreskartenbesitzer das Schwimmbad besuchen, kleiner als  ist.
ist.
(5)
Beschreibe im Sachzusammenhang ein Zufallsexperiment, das durch das abgebildete Baumdiagramm dargestellt wird.
Gib ein Ereignis an, dessen Wahrscheinlichkeit beträgt.
beträgt.
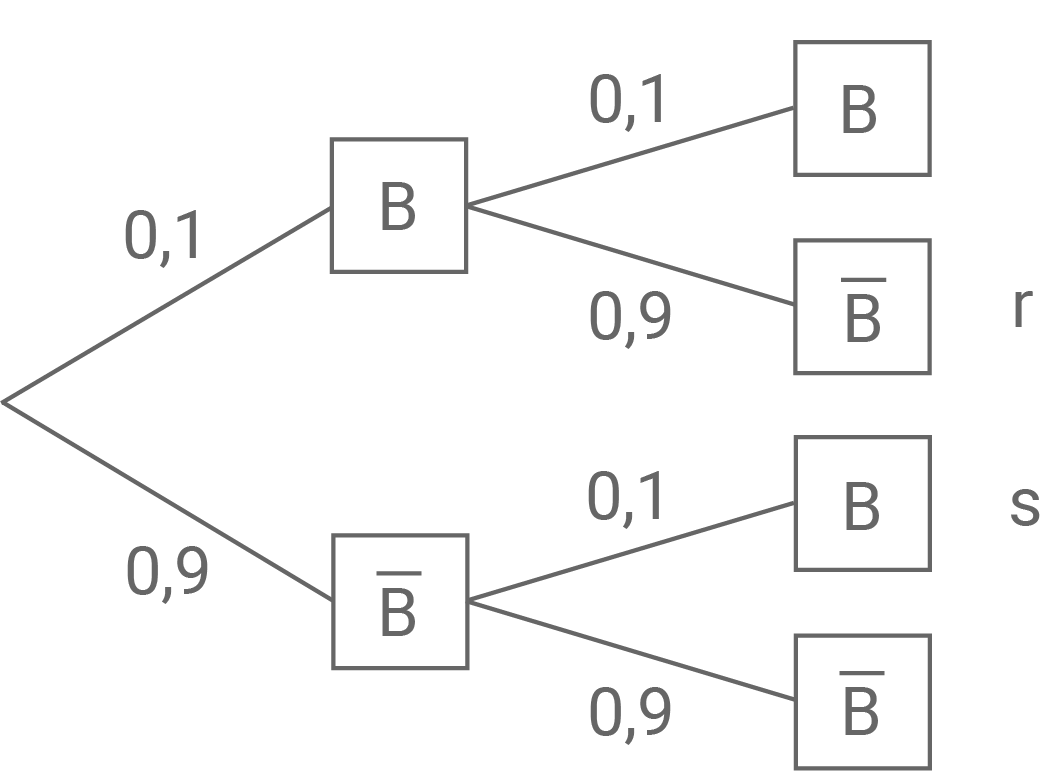
Gib ein Ereignis an, dessen Wahrscheinlichkeit

Abbildung 1
(2 + 3 + 6 + 4 + 4 Punkte)
b)
Auf dem Gelände des Schwimmbades wird ein Kiosk betrieben. Der Besitzer nimmt vereinfachend an, dass jeder Gast 
 oder gar kein Geld an seinem Kiosk ausgibt. Die Wahrscheinlichkeit, dass ein Gast
oder gar kein Geld an seinem Kiosk ausgibt. Die Wahrscheinlichkeit, dass ein Gast  ausgibt, betrage
ausgibt, betrage  die Wahrscheinlichkeit, dass ein Gast
die Wahrscheinlichkeit, dass ein Gast  ausgibt, betrage
ausgibt, betrage 
(1)
An dem betrachteten Tag besuchen  Personen das Bad. Bestimme die Höhe der Einnahmen, mit denen der Besitzer des Kiosks rechnen kann.
Personen das Bad. Bestimme die Höhe der Einnahmen, mit denen der Besitzer des Kiosks rechnen kann.
(2)
Ermittle die Wahrscheinlichkeit dafür, dass der Besitzer des Kiosks an dem betrachteten Tag erwartete Einnahmen von den Jahreskartenbesitzern hat, die mindestens  betragen.
betragen.
(3 + 4 Punkte)
c)
An einem bestimmten Tag ist das Schwimmbad zwischen 07:00 Uhr und 21:00 Uhr geöffnet. Es soll davon ausgegangen werden, dass der Zeitpunkt, zu dem ein zufällig ausgewählter Badegast das Schwimmbad betritt, mithilfe einer normalverteilten Zufallsgröße mit dem Erwartungswert  und der Standardabweichung
und der Standardabweichung  beschrieben werden kann. Die zugehörige Dichtefunktion ist in der Abbildung 2 dargestellt; dabei ist
beschrieben werden kann. Die zugehörige Dichtefunktion ist in der Abbildung 2 dargestellt; dabei ist  die seit 00:00 Uhr vergangene Zeit in Stunden.
die seit 00:00 Uhr vergangene Zeit in Stunden.
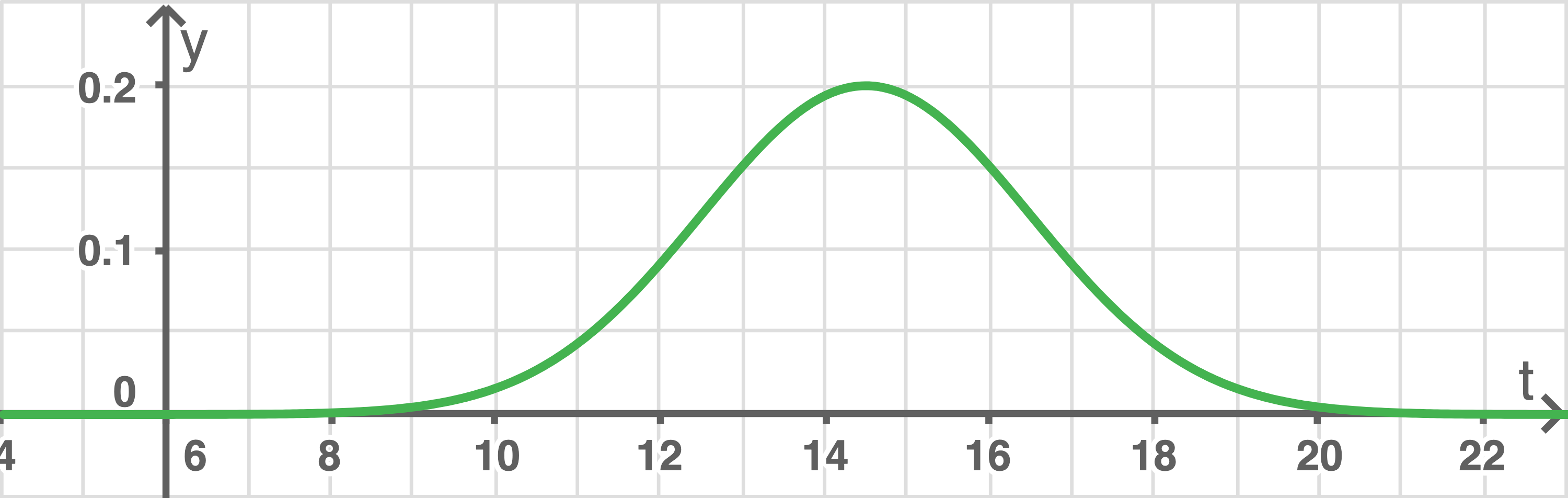

Abbildung 2
(1)
Gib den Zeitraum mit einer Länge von einer Stunde an, für den mit der größten Anzahl eintreffender Badegäste zu rechnen ist.
(2)
Ermittle graphisch, ob die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Badegast das Schwimmbad zwischen 12:00 Uhr und 16:00 Uhr betritt, größer als  ist.
ist.
Erläutere dein Vorgehen.
Erläutere dein Vorgehen.
(3)
Am betrachteten Tag wird das Schwimmbad von  Badegästen besucht. Ermittle, zu welchem Zeitpunkt mit dem Eintreffen des eintausendfünfhundertsten Badegasts zu rechnen ist.
Badegästen besucht. Ermittle, zu welchem Zeitpunkt mit dem Eintreffen des eintausendfünfhundertsten Badegasts zu rechnen ist.
(4)
Beurteile mit Hilfe einer Rechnung die folgende Argumentation:
„Das Schwimmbad ist nur zwischen 07:00 Uhr und 21:00 Uhr geöffnet. Deshalb ist es nicht sinnvoll, das Eintreffen der Badegäste mithilfe einer normalverteilten Zufallsgröße zu beschreiben, die für alle reellen Zahlen definiert ist.“
(2 + 4 + 4 + 4 Punkte)
a)
(1)
Mit einer Wahrscheinlichkeit von ca.  besuchen an einem bestimmten Tag genau
besuchen an einem bestimmten Tag genau  Jahreskartenbesitzer das Schwimmbad.
Jahreskartenbesitzer das Schwimmbad.
(2)
Die Zufallsgröße  ist binomialverteilt mit
ist binomialverteilt mit  und
und 
 Mit dem GTR folgt:
Mit dem GTR folgt:
 TI 84-PLUS
TI 84-PLUS
 Casio fx-CG
Mit einer Wahrscheinlichkeit von ca.
Casio fx-CG
Mit einer Wahrscheinlichkeit von ca.  besuchen mehr als
besuchen mehr als  Jahreskartenbesitzer das Schwimmbad.
Jahreskartenbesitzer das Schwimmbad.
2nd  vars (distr)
vars (distr)  B: binomcdf
B: binomcdf
Statistik: F5: DIST  F5: BINOM
F5: BINOM  F2: Bcd
F2: Bcd
(3)
Da die Zufallsgröße  binomialverteilt ist, folgt:
Für die Wahrscheinlichkeit folgt:
Mit einer Wahrscheinlichkeit von ca.
binomialverteilt ist, folgt:
Für die Wahrscheinlichkeit folgt:
Mit einer Wahrscheinlichkeit von ca.  weicht der Wert von
weicht der Wert von  um höchstens eine halbe Standardabweichung vom Erwartungswert der Zufallsgröße ab.
um höchstens eine halbe Standardabweichung vom Erwartungswert der Zufallsgröße ab.
(4)
Gesucht ist das größte  mit:
mit:
 Durch systematisches Ausprobieren mit dem GTR folgt:
und
Also ist
Durch systematisches Ausprobieren mit dem GTR folgt:
und
Also ist 
(5)
Zwei der  Jahreskartenbesitzer werden zufällig ausgewählt und es wird überprüft, ob diese an diesem Tag das Schwimmbad besuchen.
An dem betrachteten Tag besuchen entweder beide überprüften Jahreskartenbesitzer oder keiner von beiden das Schwimmbad.
Jahreskartenbesitzer werden zufällig ausgewählt und es wird überprüft, ob diese an diesem Tag das Schwimmbad besuchen.
An dem betrachteten Tag besuchen entweder beide überprüften Jahreskartenbesitzer oder keiner von beiden das Schwimmbad.
b)
(1)
(2)
c)
(1)
Im Zeitraum von  bis
bis  ist mit der größten Anzahl eintreffender Badegäste zu rechnen.
ist mit der größten Anzahl eintreffender Badegäste zu rechnen.
(2)
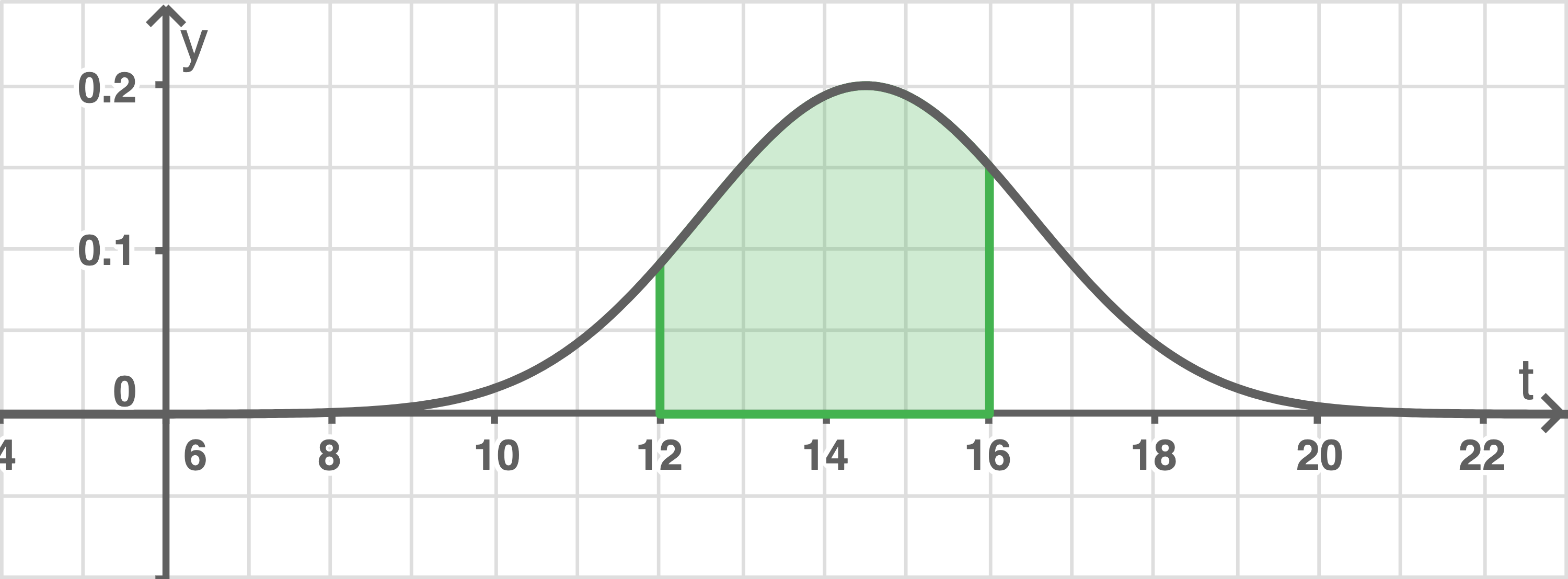
Die Fläche ist eindeutig größer als
Die zugehörige gesuchte Wahrscheinlichkeit ist damit größer als
(3)
Am betrachteten Tag betreten  Badegäste das Schwimmbad. Wenn der Eintausendfünfhundertste Badegast das Schwimmbad betritt, haben
Badegäste das Schwimmbad. Wenn der Eintausendfünfhundertste Badegast das Schwimmbad betritt, haben  der Badegäste das Schwimmbad betreten. Es ist also der Zeitpunkt gesucht, bis zu dem ein Badegast mit einer Wahrscheinlichkeit von
der Badegäste das Schwimmbad betreten. Es ist also der Zeitpunkt gesucht, bis zu dem ein Badegast mit einer Wahrscheinlichkeit von  das Schwimmbad betreten hat.
das Schwimmbad betreten hat.
 ist die Zufallsgröße, die die zufällige Uhrzeit beschreibt, zu der ein Besucher des Schwimmbades das Schwimmbad betritt. Diese ist laut Aufgabenstellung normalverteilt mit
ist die Zufallsgröße, die die zufällige Uhrzeit beschreibt, zu der ein Besucher des Schwimmbades das Schwimmbad betritt. Diese ist laut Aufgabenstellung normalverteilt mit  und
und 
Bestimmt wird also mit
mit  Dazu wird
Dazu wird  als Funktion aufgefasst und mittels des GTRs graphisch dargestellt.
als Funktion aufgefasst und mittels des GTRs graphisch dargestellt.
 TI 84-PLUS
Zu bestimmen sind die Schnittpunkte des Graphen von
TI 84-PLUS
Zu bestimmen sind die Schnittpunkte des Graphen von  mit der Gerade zu
mit der Gerade zu 
 Casio fx-CG
Zu bestimmen ist der
Casio fx-CG
Zu bestimmen ist der  -Wert zum
-Wert zum  -Wert
-Wert  mit dem X-CAL-Befehl.
Es ergibt sich
mit dem X-CAL-Befehl.
Es ergibt sich  Etwa gegen
Etwa gegen  kann man damit rechnen, dass der Eintausendfünfhundertste Besucher das Schwimmbad betritt.
kann man damit rechnen, dass der Eintausendfünfhundertste Besucher das Schwimmbad betritt.
Bestimmt wird also
2nd  trace (calc)
trace (calc)  5: intersect
5: intersect
F5 (G-Solv)  F6
F6  F2: X-CAL
F2: X-CAL
(4)
Argumentation beurteilen
Die Argumentation würde nur dann greifen, wenn eine nicht vernachlässigbare Wahrscheinlichkeit der Besuchszeiten außerhalb der Öffnungszeiten liegen würde.
Mit dem GTR erhält man: Die Modellierung ordnet den Zeiten außerhelb der Öffnungszeiten also eine Wahrscheinlichkeit zu, die nahezu Null und damit vernachlässigbar ist. Die Argumentation trifft auf den vorliegenden Sachverhalt also nicht zu.
Mit dem GTR erhält man: Die Modellierung ordnet den Zeiten außerhelb der Öffnungszeiten also eine Wahrscheinlichkeit zu, die nahezu Null und damit vernachlässigbar ist. Die Argumentation trifft auf den vorliegenden Sachverhalt also nicht zu.