Pflichtteil

Aufgabe 1 - Analysis

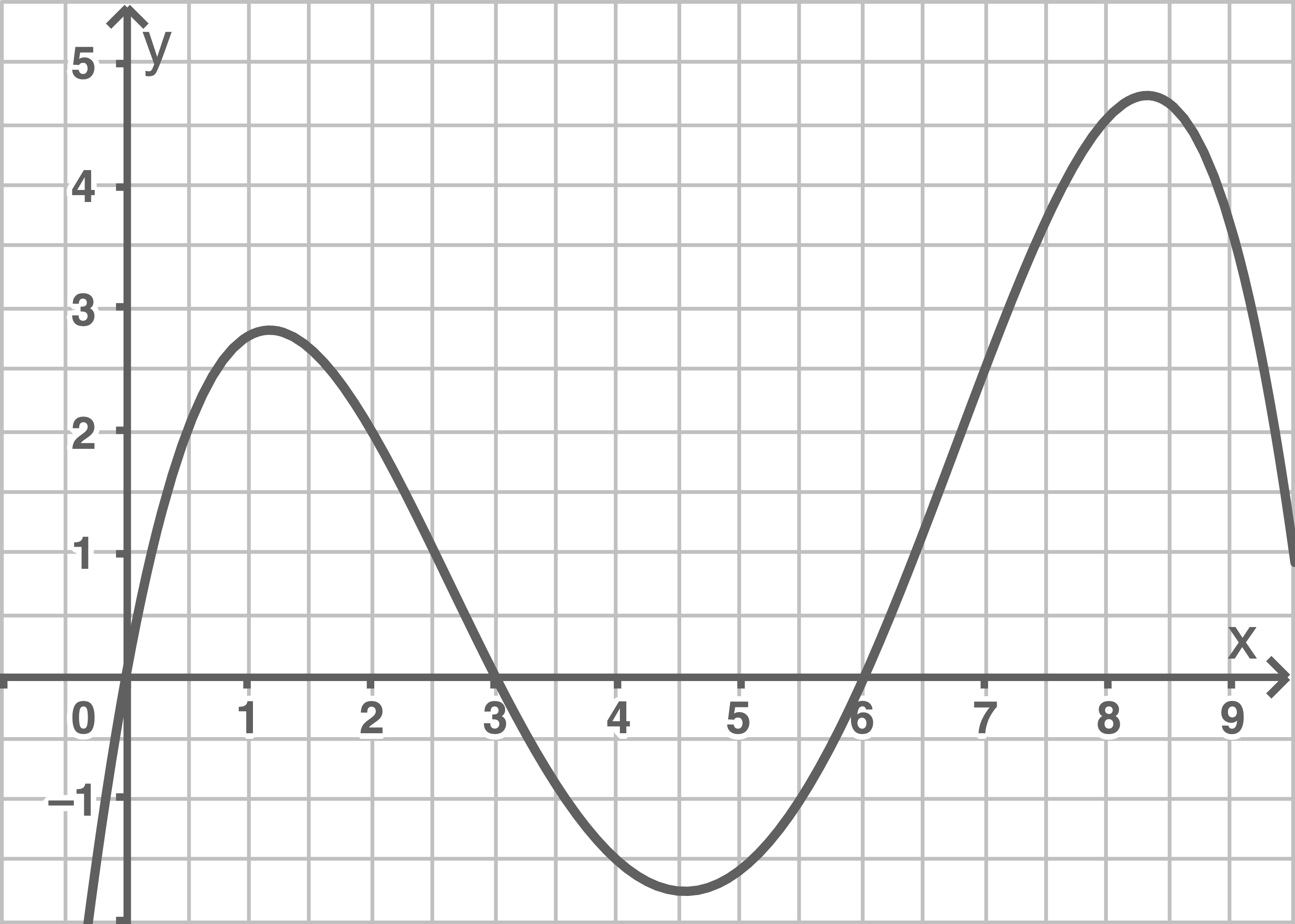
Die Abbildung zeigt den Graphen der Funktion $f.$

Begründe, dass die Ableitungsfunktion $\(f$ im Intervall $[5 ;8]$ nicht monoton ist.

Bestimme die Anzahl der Nullstellen der Funktion $I$ mit

$I(x)=\displaystyle\int_{2}^{x}f(t)\;\mathrm dt, \; 2 \leq x \leq 9.$

(2 + 3 Punkte)

Aufgabe 2 – Analysis

Ermittle eine Gleichung der quadratischen Funktion $g$ , die die beiden folgenden Eigenschaften hat:

Der Graph von $g$ schneidet die Gerade mit der Gleichung $y=\dfrac{1}{4}x + 1$ im Punkt $(0\mid 1)$ unter einem rechten Winkel.
Die $x$ - und die $y$ -Koordinate des Extrempunkts des Graphen von $g$ stimmen überein.

(5 Punkte)

Aufgabe 3 - Vektorielle Geometrie

Gegeben sind die Gerade $g:\overrightarrow x=\pmatrix{7\\3\\3}+r\cdot \pmatrix{3\\0\\-1}$ mit $r \in \mathbb{R}$ und die Ebene $E:3x-z=-2.$

Begründe, dass $g$ senkrecht zu $E$ steht.

Die Gerade $h:\overrightarrow x= \pmatrix{7\\3\\3}+s\cdot \pmatrix{1\\2\\3}$ mit $s \in \mathbb{R}$ hat mit $E$ keinen gemeinsamen Punkt. Es gibt Geraden, die in $E$ liegen und parallel zu $h$ verlaufen. Bestimme eine Gleichung derjenigen dieser Geraden, die von $h$ den kleinsten Abstand hat.

(1 + 4 Punkte)

Aufgabe 4 - Stochastik

In einer Urne befinden sich schwarze (s) und weiße (w) Kugeln. Ohne Zurücklegen wird zweimal nacheinander genau eine Kugel gezogen. Für das Zufallsexperiment gilt das untenstehende unvollständige Baumdiagramm.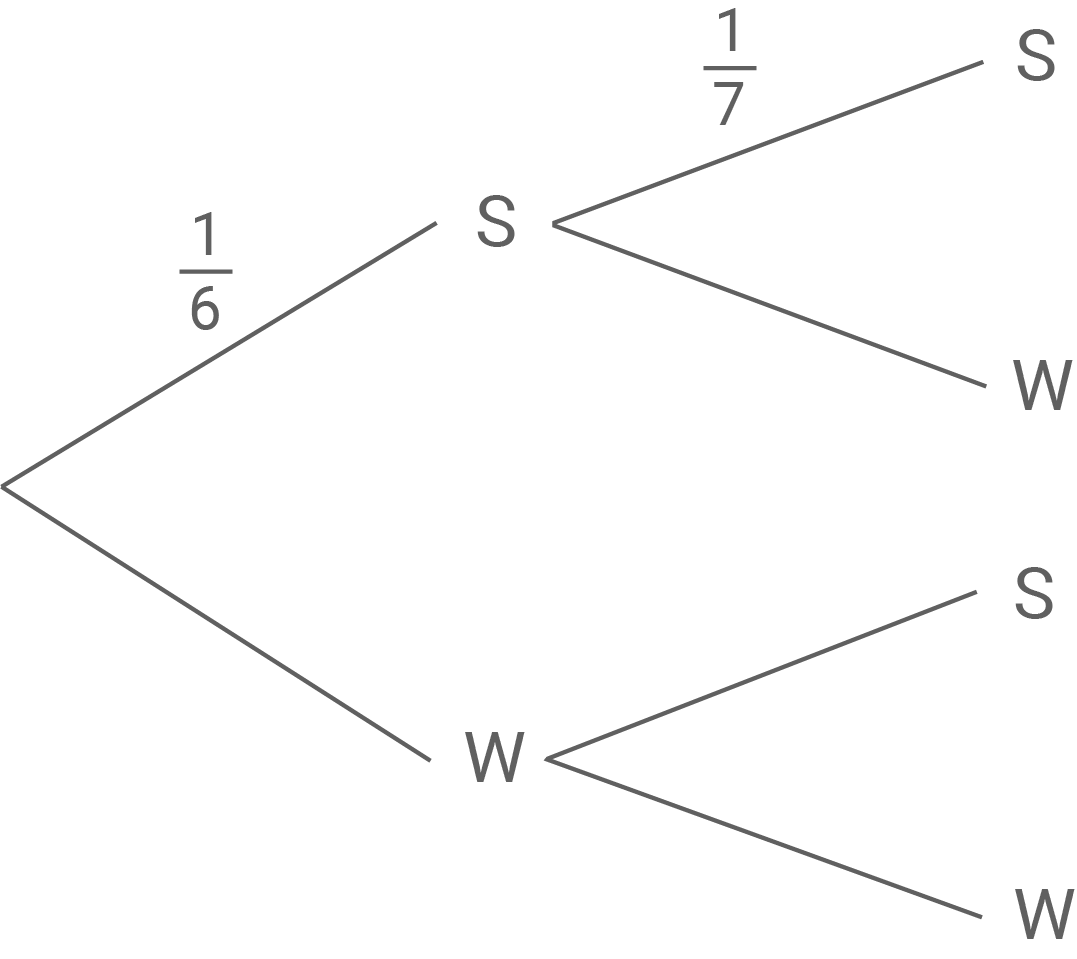

berlin mathe abi lk wtr 2022 hilfsmittelfreier teil baumdiagramm

Berechne die Wahrscheinlichkeit dafür, dass mindestens eine weiße Kugel gezogen wird.

Ermittle die Anzahl der weißen und der schwarzen Kugeln, die sich vor dem Ziehen in der Urne befanden.

(1 + 4 Punkte)

(20 Punkte)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung 1 – Analysis

Im Intervall $[5;8]$ besitzt die Funktion $f$ eine Wendestelle, weshalb $\(f$ dort eine Extremstelle hat und nicht monoton ist.

Eine Nullstelle der Funktion $I$ ist $x_1=2.$
Anhand des Verlaufs des Graphen können die Größen der Teilflächen, die der Graph von $f$ mit der $x$ -Achse einschließt, miteinander verglichen werden.

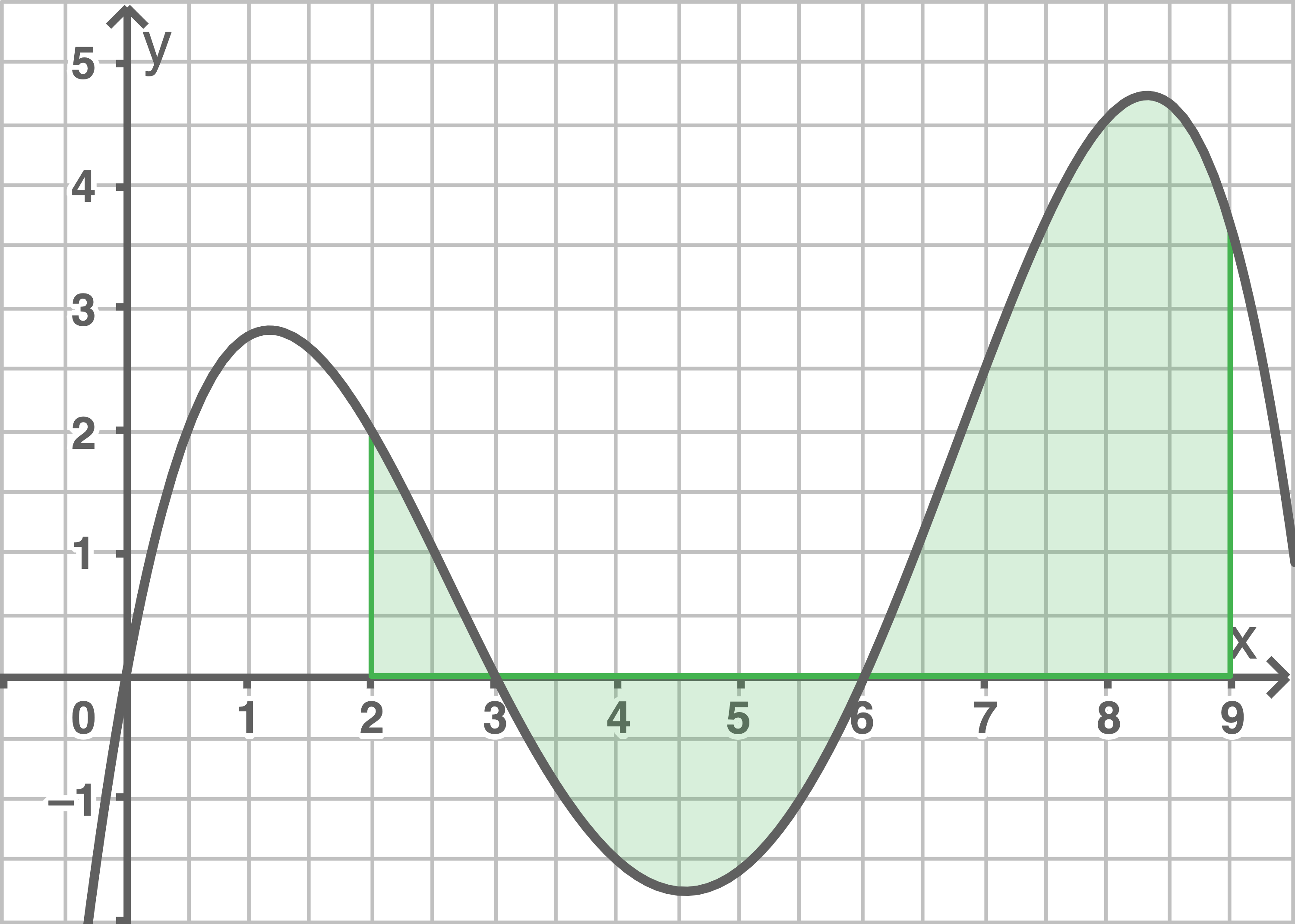Graph fünften Grades Nullstellen graphisch bestimmen

Hilfsskizze: Markierte Teilflächen, die der Graph von $f$ mit der $x$ -Achse einschließt

Es gilt:

$I(3)= \displaystyle\int_{2}^{3}f(t)\;\mathrm dt \gt 0,$

$I(6)= \displaystyle\int_{2}^{6}f(t)\;\mathrm dt\lt 0$ und

$I(9)= \displaystyle\int_{2}^{9}f(t)\;\mathrm dt \gt 0.$

Wegen des Vorzeichenwechsels muss zwischen diesen Stellen je eine Nullstelle von $I$ liegen. Im Intervall $[2 ; 9]$ befinden sich folglich insgesamt drei Nullstellen.

Lösung 2 – Analysis

Gleichung einer quadratischen Funktion:

$g(x)=ax^2+bx+c$

Aus dem Schnittpunkt mit der Gerade $y$ folgt, dass die Gerade ebenfalls durch den Punkt $(0 \mid 1)$ verläuft.

$\begin{array}[t]{rll} g(0)&=& 1& \\[5pt] a\cdot 0^2+b\cdot 0+c&=& 1& \\[5pt] c&=&1 \end{array}$

Der Schnittwinkel von $90^{\circ}$ weist auf Orthogonalität hin. Für den Punkt $(0\mid 1)$ gilt also:

$\(g$

Eingesetzt in $\(g$ ergibt sich so:

$\(g$

Somit gilt:

$\(\begin{array}[t]{rll} g$

Extremstelle bestimmen:

Notwendige Bedingung für Extremstellen anwenden:

$\(\begin{array}[t]{rll} g$

Da bereits vorausgesetzt ist, dass ein Extrempunkt existiert, ist das Prüfen der hinreichenden Bedingung hier nicht mehr nötig.

$\begin{array}[t]{rll} g\left(\dfrac{2}{a}\right)&=&\dfrac{2}{a} & \\[5pt] a\cdot\left(\dfrac{2}{a}\right)^2-4\cdot \left(\dfrac{2}{a}\right)+1&=&\dfrac{2}{a} & \\[5pt] a\cdot\dfrac{4}{a^2}-\dfrac{8}{a}+1&=&\dfrac{2}{a} & \\[5pt] -\dfrac{4}{a}+1&=&\dfrac{2}{a} &\quad \scriptsize \mid\; \cdot a \\[5pt] -4+a&=& 2 &\quad \scriptsize \mid\; +4 \\[5pt] a&=& 6 & \\[5pt] \end{array}$

Somit folgt: $g(x)=6x^2-4x+1$

Lösung 3 – Vektorielle Geometrie

Ein Normalenvektor von $E$ ist gegeben durch $\overrightarrow{n_E}=\pmatrix{3\\0\\-1}.$ Dieser stimmt mit dem Richtungsvektor von $g$ überein. Damit steht $g$ senkrecht zu $E.$

Gesucht ist eine Gerade, die durch den Schnittpunkt von $E$ und $g$ verläuft und parallel zu $h$ ist.

1. Schritt: Schnittpunkt bestimmen

Koordinaten der Geraden in die Ebenengleichung einsetzen:

$\begin{array}[t]{rll} 3\cdot (7+3r)-(3-r)&=& -2 \\[5pt] 18+10r&=& -2 \quad \scriptsize \mid\; -18 \\[5pt] 10r&=& -20 \quad \scriptsize \mid\; :10 \\[5pt] r&=& -2 \end{array}$

Einsetzen in die Geradengleichung von $g$ liefert die Koordinaten des Schnittpunktes:

$\overrightarrow{OS}=\pmatrix{7\\3\\3} -2\cdot \pmatrix{3\\0\\-1}$ $=\pmatrix{1\\3\\5}$

$S(1\mid 3 \mid 5).$

2. Schritt: Geradengleichung aufstellen

Der Schnittpunkt $S$ ist der Stützvektor der gesuchten Gerade. Da diese parallel zu $h$ verlaufen soll, hat sie den gleichen Richtungsvektor. Die gesuchte Geradengleichung lautet somit:

$\overrightarrow{x}= \pmatrix{1\\3\\5}+s\cdot \pmatrix{1\\2\\3}$

Lösung 4 – Stochastik

$P(E)=1-P(S S)=1-\dfrac{1}{6} \cdot \dfrac{1}{7}$ $=\dfrac{41}{42}$

Die Variable $s$ bezeichnet die Anzahl der schwarzen Kugeln, die Variable $a$ die Anzahl aller Kugeln.

Die Wahrscheinlichkeit, im ersten Zug eine schwarze Kugel zu ziehen, beträgt $\dfrac{1}{6}.$ Es muss also $\dfrac{s}{a}=\dfrac{1}{6}$ gelten, daraus folgt $a=6s.$

Wenn im ersten Zug eine schwarze Kugel gezogen wurde, gilt für den zweiten Zug $\dfrac{s-1}{a-1}=\dfrac{1}{7}.$ Daraus folgt $7(s-1)=a-1.$

Einsetzen von $a=6s$ liefert:

$\begin{array}[t]{rll} 7(s-1)&=& 6s-1 \\[5pt] 7s-7&=& 6s-1 \quad \scriptsize \mid\; +7 \\[5pt] 7s&=& 6s+6 \quad \scriptsize \mid\; -6s \\[5pt] s&=& 6 \end{array}$

Die Gesamtzahl der Kugeln ist folglich gegeben durch $a=6s=6\cdot 6=36.$

Vor dem Ziehen befanden sich $6$ schwarze und $36-6=30$ weiße Kugeln in der Urne.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?