Aufgabe 2

Gegeben ist die Funktion $f$ mit

$f(x)= -\dfrac{1}{10^6}x^4+\dfrac{4}{9375}x^3-\dfrac{13}{250}x^2+\dfrac{8}{5}x+140$

mit Definitionsbereich $\mathbb{R}.$

(1)

Berechne die Koordinaten der Extrempunkte des Graphen von $f$ und bestimme die Art der Extrempunkte.
[Zur Kontrolle: Die Extremstellen sind $20,$ $100$ und $200.$ ]

(2)

Begründe ohne weitere Rechnung, dass die Funktion $f$ genau zwei Wendestellen besitzt.

(3)

Gib die Koordinaten des Schnittpunkts des Graphen von $f$ mit der $y$ -Achse an.
Begründe ohne weitere Rechnung, dass $f$ genau zwei Nullstellen hat.

(7 + 3 + 4 Punkte)

Für $50\lt x \lt 130$ gibt es ein Paar von $x$ -Werten, die sich um $60$ unterscheiden und für die die zugehörigen Funktionswerte übereinstimmen.
Bestimme dieses Paar von $x$ -Werten und gib den zugehörigen Funktionswert an.

(5 Punkte)

Der Graph von $f$ schließt mit den Koordinatenachsen und der Geraden mit der Gleichung $x=240$ ein Flächenstück ein.
Bestimme eine Gleichung der Geraden, die parallel zur $y$ -Achse verläuft und dieses Flächenstück halbiert.

(5 Punkte)

Für $u\approx 217$ gilt die nachfolgende Aussage:

$\dfrac{1}{2} \cdot u \cdot f(u) + \displaystyle\int_{u}^{240}f(x)\;\mathrm dx = \frac{2}{3}\cdot \displaystyle\int_{0}^{240}f(x)\;\mathrm dx$

Erläutere diese Aussage unter Verwendung einer Skizze.
Hinweis: Nutze für die Skizze die nachfolgende Abbildung.

(5 Punkte)

Abbildung 1: Graph von $f$

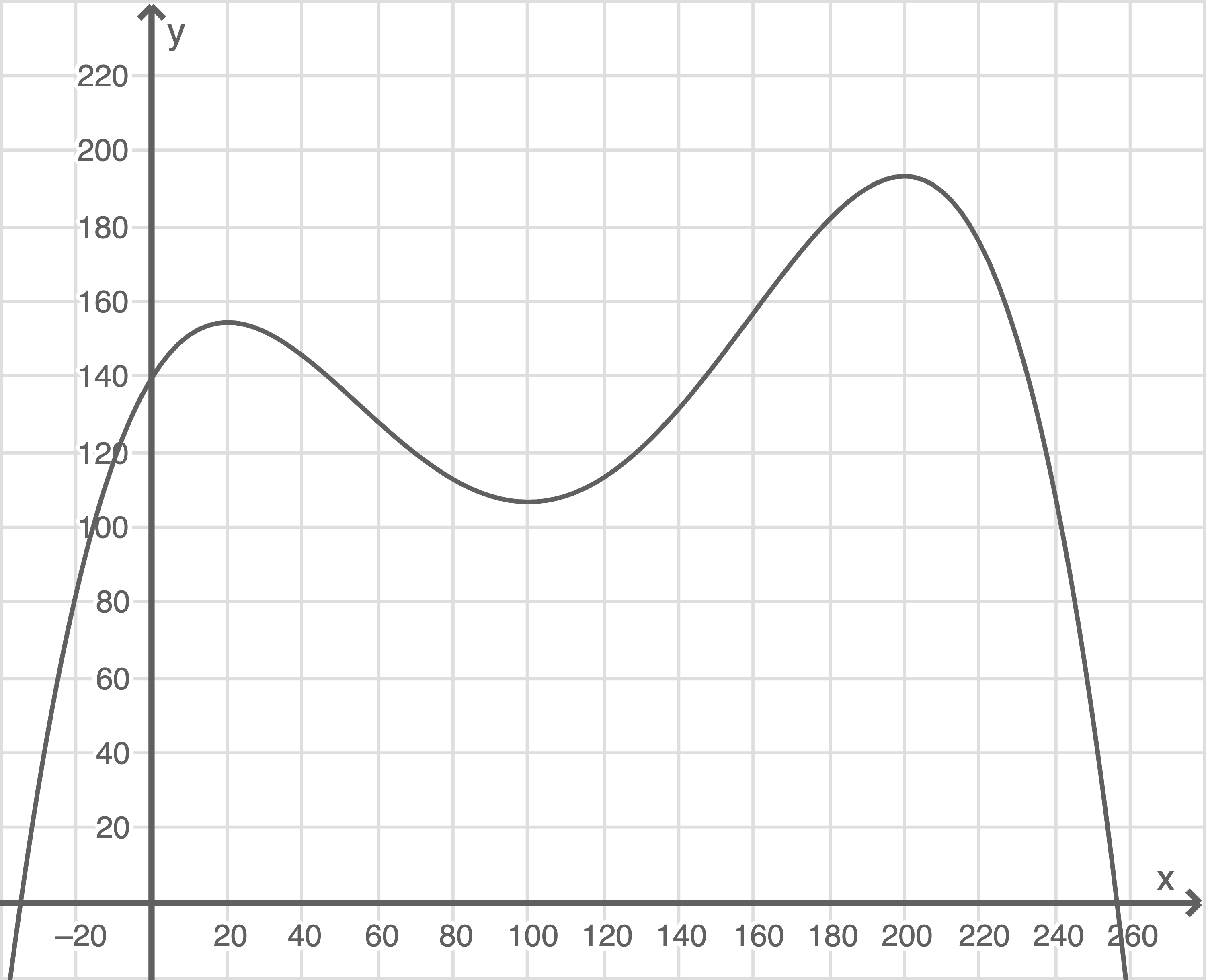
Diabetespatientinnen und -patienten haben die Möglichkeit, mithilfe sogenannter CGM-Geräte ihren Glukosewert, d.h. den Anteil der Glukose im Blut, ständig zu messen. Die gegebene Funktion $f$ beschreibt für $0 \leq x \leq 240$ modellhaft die Entwicklung des Glukosewerts eines Patienten. Dabei ist $x$ die seit Beobachtungsbeginn vergangene Zeit in Minuten und $f(x)$ der Glukosewert in Milligramm pro Deziliter $\left(\dfrac{\text{mg}}{\text{dl}}\right).$

Hohe Glukosewerte über längere Zeit gelten als Risikofaktor.
Ermittle für den betrachteten Zeitraum, wie lange Glukosewerte über $170\,\dfrac{\text{mg}}{\text{dl}}$ gemessen wurden.

(5 Punkte)

Bestimme für den betrachteten Zeitraum denjenigen Zeitpunkt, zu dem der Glukosewert am stärksten ansteigt.

(6 Punkte)

(1)

1. Schritt: Ableitungen bilden

$\(\begin{array}[t]{rll} f(x) &=& -\dfrac{1}{10^6}x^4+\dfrac{4}{9375}x^3-\dfrac{13}{250}x^2+\dfrac{8}{5}x+140 \\[5pt] f$

2. Schritt: Notwendiges Kriterium für Extremstellen anwenden

$\(\begin{array}[t]{rll} f$

Mit dem GTR können die Nullstellen des Graphen von $\(f$ graphisch ermittelt werden.

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ trace (calc) $\to$ 2: zero

$\blacktriangleright$ Casio fx-CG

F5 (G-Solv) $\to$ F1: ROOT

Mögliche Extremstellen besitzt $f$ also bei $x_1=20,$ $x_2=100$ und $x_3=200.$ Weitere kann es nicht geben, da es sich bei $\(f$ um eine ganzrationale Funktion dritten Grades handelt und eine solche Funktion maximal drei Nullstellen annehmen kann.

3. Schritt: Hinreichendes Kriterium für Extremstellen anwenden

$\(\begin{array}[t]{rll} f$

An den Stellen $x_1=20$ und $x_2=200$ besitzt der Graph von $f$ also einen Hochpunkt, an der Stelle $x_2=100$ einen Tiefpunkt.

4. Schritt: $y$ -Koordinaten der Extrempunkte berechnen

$\begin{array}[t]{rll} f(20)&=& -\frac{1}{10^6}\cdot 20^4+\frac{4}{9375}\cdot 20^3-\frac{13}{250}\cdot 20^2+\frac{8}{5}\cdot 20+140 \\[5pt] &=& \frac{11584}{75} \\[5pt] &\approx& 154,45 \\[10pt] f(100)&=& -\frac{1}{10^6}\cdot 100^4+\frac{4}{9375}\cdot 100^3-\frac{13}{250}\cdot 100^2+\frac{8}{5}\cdot 100+140 \\[5pt] &=& \frac{320}{3} \\[5pt] &\approx& 106,67 \\[10pt] f(200)&=& -\frac{1}{10^6}\cdot 200^4+\frac{4}{9375}\cdot 200^3-\frac{13}{250}\cdot 200^2+\frac{8}{5}\cdot 200+140 \\[5pt] &=& \frac{580}{3} \\[5pt] &\approx& 193,33 \\[10pt] \end{array}$

Der Graph von $f$ besitzt zwei Hochpunkte $H_1(20\mid \frac{11584}{75})$ und $H_2(200\mid \frac{580}{3})$ sowie einen Tiefpunkt $T(100\mid \frac{320}{3}).$

(2)

Das notwendige Kriterium für eine Wendestelle $x_W$ von $f$ lautet $\(f$ Bei $\(f$ handelt es sich um eine ganzrationale Funktion zweiten Grades. Diese kann also maximal zwei Nullstellen besitzen. $f$ kann daher maximal zwei Wendestellen besitzen.
Der Graph von $f$ besitzt nach a) (1) genau drei Extrempunkte. Im Hochpunkt ist der Graph immer rechtsgekrümmt, in einem Tiefpunkt immer linksgekrümmt. Zwischen zwei Extrempunkten muss der Graph seine Krümmung daher in einem Punkt ändern. Dies ist die Definition eines Wendepunkts. Der Graph von $f$ muss also mindestens zwei Wendepunkte besitzen - einen zwischen $H_1$ und $T$ und einen zwischen $T$ und $H_2.$

Da er gleichzeitig höchstens zwei Wendepunkte besitzen kann, besitzt der Graph von $f$ also genau zwei Wendepunkte.

(3)

$\begin{array}[t]{rll} f(0)&=&-\frac{1}{10^6}\cdot 0^4+\frac{4}{9375}\cdot 0^3-\frac{13}{250}\cdot 0^2+\frac{8}{5}\cdot 0+140 \\[5pt] &=& 140 \\[5pt] \end{array}$

Der Graph von $f$ schneidet die $y$ -Achse im Punkt $S_y(0\mid 140).$

Die drei Extrempunkte des Graphen von $f$ liegen oberhalb der $x$ -Achse. Im Intervall $[20;200]$ kann $f$ daher keine Nullstellen besitzen, da sonst der Tiefpunkt eine negative $y$ -Koordinate annehmen würde.

Da $\lim\limits_{x\to-\infty}f(x) = -\infty$ und $\lim\limits_{x\to+\infty}f(x) = -\infty$ gilt, muss der Graph von $f$ aber für $x\lt 20$ genau einmal die $x$ -Achse schneiden. Würde er sie zweimal schneiden, gäbe es für $x\lt 20$ noch einen weiteren Tiefpunkt. Gleiches gilt für $x\gt 200.$ Insgesamt besitzt $f$ daher genau zwei Nullstellen.

Gleichunganzeigen

$f(x) = f(x+60)$

Diese Gleichung wird mit dem solve-Befehl des GTRs gelöst.

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ trace (calc) $\to$ 5: intersect

$\blacktriangleright$ Casio fx-CG

F5 (G-Solv) $\to$ F5: INTSECT

Es ergibt sich $x \approx 69,1528.$
Das gesuchte Paar von $x$ -Werten ist also $x_1\approx 69,1528$ und $x_2\approx 129,1528.$ Diese haben einen Abstand von $60$ und den gemeinsamen Funktionswert $f(69,1528)\approx 120,203.$

Gesucht ist eine Gerade $x=b$ mit:

$\dfrac{1}{2}\displaystyle\int_{0}^{240}f(x)\;\mathrm dx$ $= \displaystyle\int_{0}^{b}f(x)\;\mathrm dx$

Der Wert des Integrals $\dfrac{1}{2}\displaystyle\int_{0}^{240}f(x)\;\mathrm dx$ wird mit dem GTR bestimmt:

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ trace (calc) $\to$ 7: $\int f(x)\;\mathrm dx$

$\blacktriangleright$ Casio fx-CG

F5 (G-Solv) $\to$ F6 $\to$ F3: $\int \;\mathrm dx$

$\dfrac{1}{2}\displaystyle\int_{0}^{240}f(x)\;\mathrm dx$ $\approx \dfrac{1}{2}\cdot 34705,92$ $= 17352,96$

Es gilt:

Rechenweg anzeigen

$-\frac{1}{10^6\cdot 5}b^5+\frac{1}{9375}b^4-\frac{13}{750}b^3+\frac{4}{5}b^2+140\cdot b = 17352,96$

Die Gleichung wird mit dem GTR graphisch gelöst:

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ trace (calc) $\to$ 5: intersect

$\blacktriangleright$ Casio fx-CG

F5 (G-Solv) $\to$ F6 $\to$ F2: X-CAL

Es ergibt sich $b \approx 135,46.$ Eine Gleichung der Geraden, die das Flächenstück halbiert lautet $x =135,46.$

Die Gleichung lä;sst sich in drei Bestandteile teilen, die jeweils den Flächeninhalt einer Fläche beschreiben:

Die Summe aus $A_1$ und $A_2$ entspricht $\frac{2}{3}$ des Flächeninhalts, den der Graph von $f$ im Bereich $0\leq x \leq 240$ mit den Koordinatenachsen einschließt.

Mit dem GTR werden die $x$ -Werte für $f(x)=170$ graphisch ermittelt. Es ergeben sich:

$x_1 \approx 169,84$ und $x_2\approx 222,77$

Dazwischen liegt der Hochpunkt $H_2$ mit der $y$ -Koordinate $193,33.$

Es werden also ca. $53$ Minuten lang Glukosewerte über $170\,\frac{\text{mg}}{\text{dl}}$ gemessen.

Gesucht ist also das absolute Maximum von $\(f$ im Bereich $0\leq x\leq 240.$
Die lokalen Maxima von $\(f$ werden mit dem GTR graphisch bestimmt:

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ trace (calc) $\to$ 4: maximum

$\blacktriangleright$ Casio fx-CG

F5 (G-Solv) $\to$ F2: MAX

Die Koordinaten des Hochpunktes des Graphen von $f$ ergeben sich zu $H(158,74 \mid 1,35).$

Für die Intervallränder gilt:

$\(\begin{array}[t]{rll} f$

An der Stelle $x=240$ fällt der Glukosewert, da $\(f$ negativ ist.
Der Glukosewert steigt also zu Beginn des betrachteten Zeitraums, $x=0,$ am stärksten an.