A2

Gegeben sind die in $\mathbb{R}$ definierten ganzrationalen Funktionen $f_k$ mit $f_k(x)=x^4+(2-k)\cdot x^3-k\cdot x^2$ mit $k\in\mathbb{R}.$

(1)

Begründe, dass der Graph von $f_2$ symmetrisch bezüglich der $y$ -Achse ist.

(2)

Es gibt einen Wert von $k,$ für den $x = 1$ eine Wendestelle von $f_k$ ist.
Berechne diesen Wert von $k.$

(1 + 4 Punkte)

Eine Funktionenschar $f_k$ ist gegeben durch die Gleichung $f_k(x)=\dfrac{1}{k}\cdot x\cdot \mathbb{e}^{-k^2\cdot x},$ $x\in\mathbb{R},$ $k\in\mathbb{R},$ $k\neq0.$

(1)

Zeige rechnerisch: $\(f$

Im Folgenden kannst du verwenden: $\(f$

(2)

Zeige, dass $\dfrac{1}{k^2}$ eine Extremstelle aller Funktionen der Schar ist, und untersuche, für welche Werte von $k$ die Funktionen der Schar an der Stelle $\dfrac{1}{k^2}$ ein Minimum besitzen.

(2 + 3 Punkte)

Gegeben sind die Funktionen $f$ und $h$ mit den Gleichungen $f(x)=(x-3)\cdot \mathbb{e}^x,$ $x\in\mathbb{R},$ $h(x)=x-3,$ $x\in\mathbb{R}.$

(1)

Bestimme rechnerisch die beiden Schnittstellen der Graphen der Funktionen $f$ und $h.$
[Zur Kontrolle: Die Schnittstellen sind $x=0$ und $x=3.$ ]

(2)

Zwischen den Schnittstellen verläuft der Graph von $h$ oberhalb des Graphen von $f.$ Die Funktion $D(x)=(4-x)\cdot \mathbb{e}^x+0,5\cdot x^2-3\cdot x$ ist eine Stammfunktion der Funktion $d$ mit $d(x)= h(x)- f (x).$
Ermittle den Flächeninhalt der Fläche, die von den Graphen der Funktionen $h$ und $f$ eingeschlossen wird.

(3 + 2 Punkte)

Betrachtet werden die in $\mathbb{R}$ definierten Funktionen $f$ und $F,$ wobei $F$ eine Stammfunktion von $f$ ist. Die Abbildung zeigt den Graphen $G_F$ von $F.$

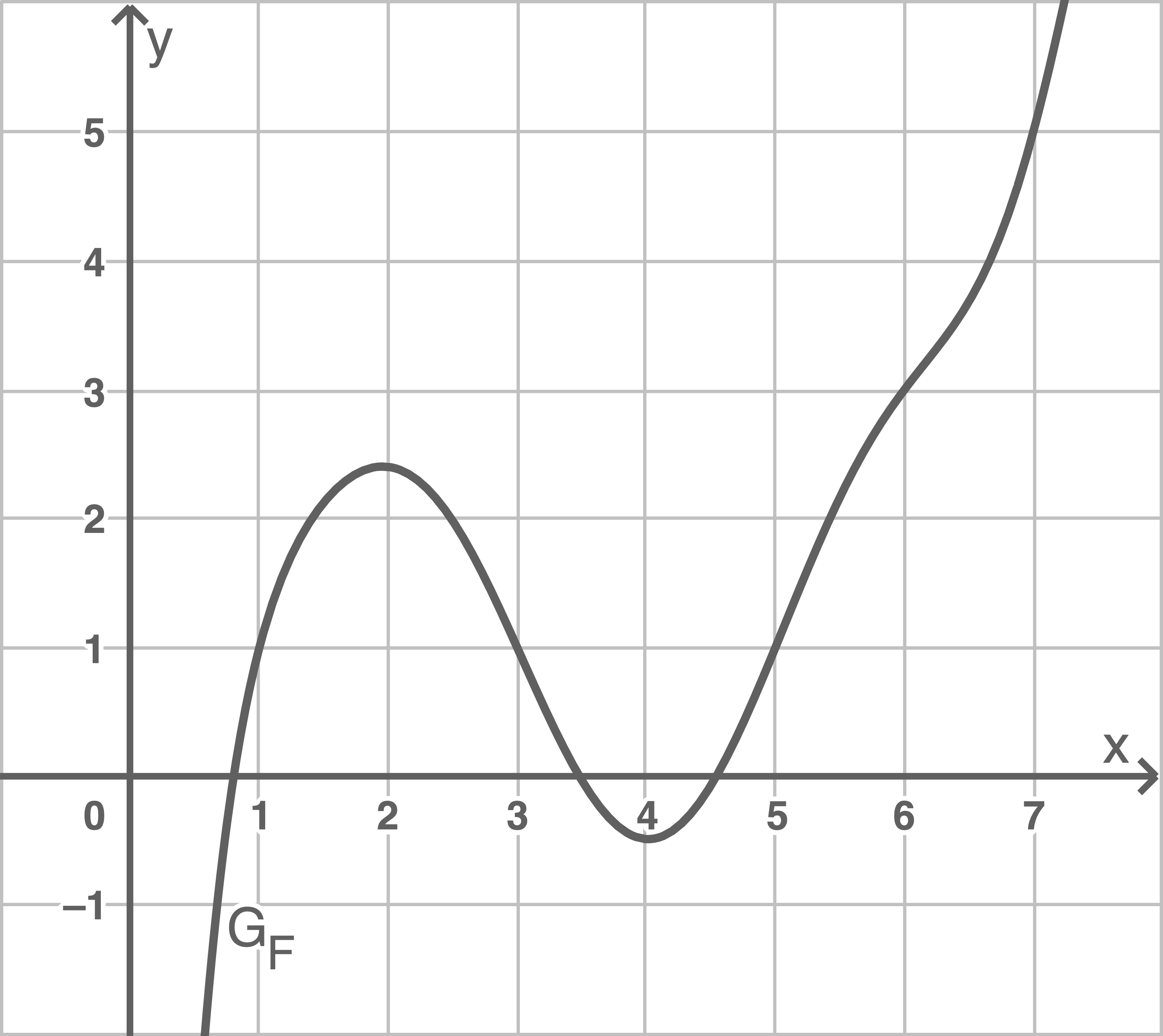
funktionswert, tangente, abbildung, stammfunktion, ableitung

(1)

Bestimme den Wert des Integrals $\displaystyle\int_{1}^{7}f(x)\;\mathrm dx.$

(2)

Bestimme grafisch näherungsweise den Funktionswert von $f$ an der Stelle $1.$

(2 + 3 Punkte)

Pia hat eine Dartscheibe geschenkt bekommen. Sie trifft im Mittel zu etwa $80\,\%$ die Dartscheibe. Die Zufallsgröße $X:$ „Anzahl der Treffer beim Pfeilwurf auf die Dartscheibe“ wird im Folgenden als binomialverteilt mit $p = 0,8$ angenommen.
Pia wirft genau 100-mal auf die Dartscheibe.

(1)

Berechne den Erwartungswert und die Standardabweichung von $X.$

(2)

Gib einen Term zur Berechnung der Wahrscheinlichkeit an, dass Pia genau 80-mal die Dartscheibe trifft, davon zehnmal in den ersten zehn Würfen.

(3)

Gib einen Term zur Berechnung der Wahrscheinlichkeit an, dass sie mindestens einmal die Dartscheibe trifft, und begründe anhand des Terms, dass diese Wahrscheinlichkeit nahezu $100\,\%$ beträgt.

(2 + 1 + 2 Punkte)

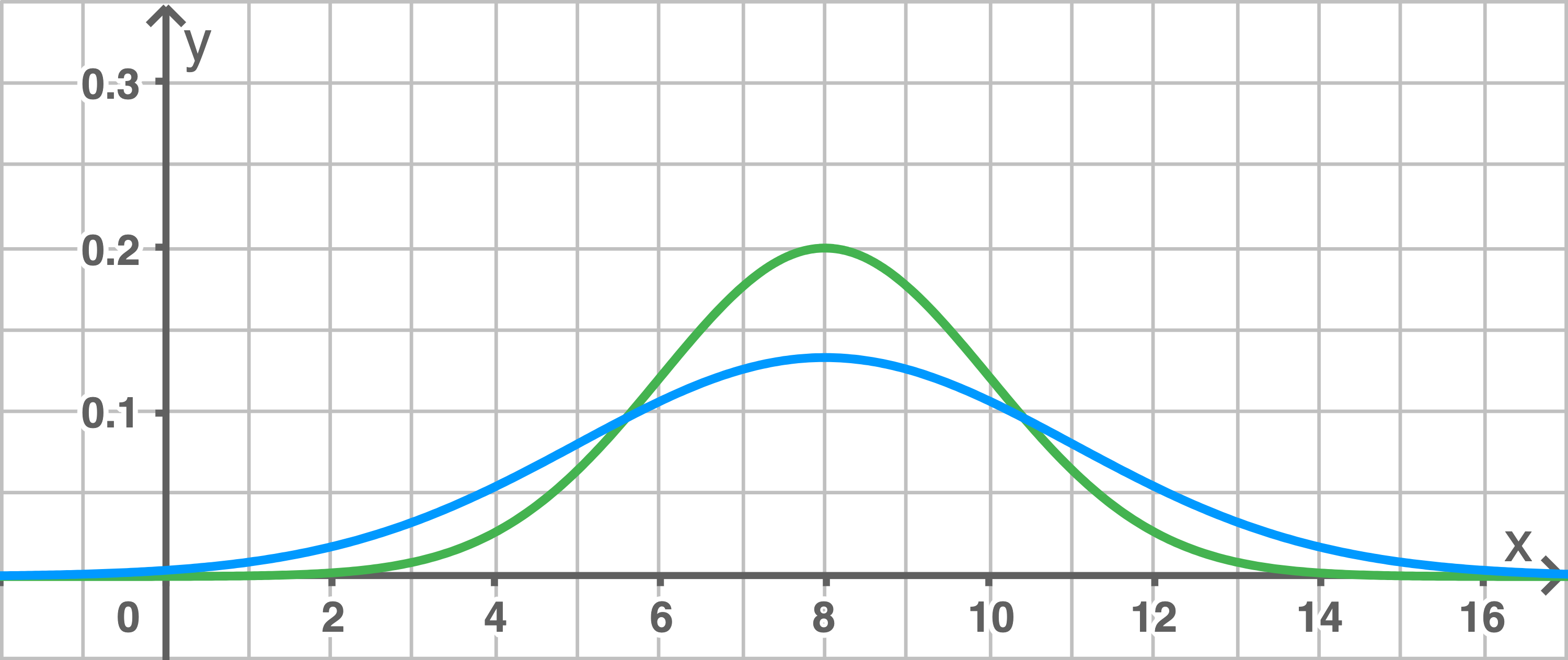
Abbildung 2 zeigt den Graphen der Dichtefunktion der normalverteilten Zufallsgröße $A.$

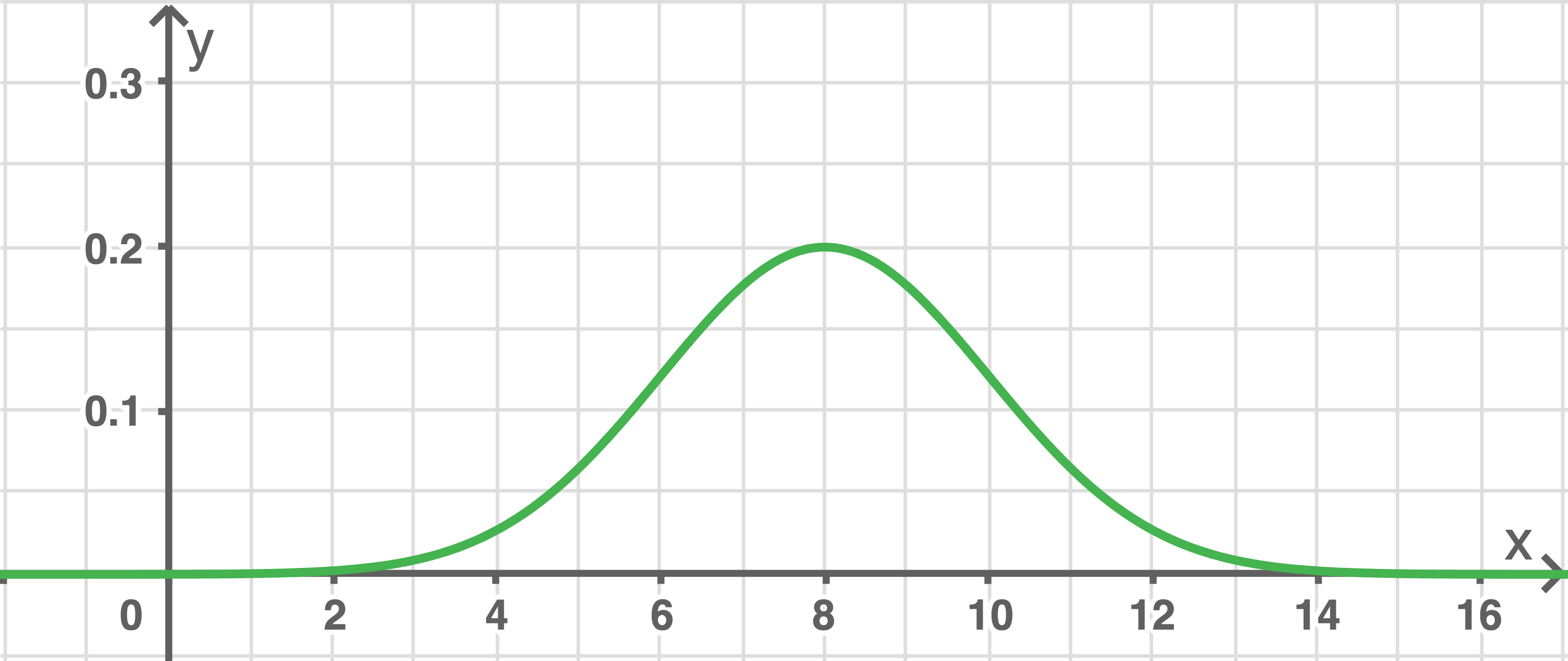
Abbildung 2

(1)

Die Wahrscheinlichkeit dafür, dass $A$ einen Wert aus dem Intervall $[6;10]$ annimmt, beträgt etwa $68\,\%.$
Berechne die Wahrscheinlichkeit dafür, dass $A$ einen Wert annimmt, der größer ist als $10.$

(2)

Die Zufallsgröße $B$ ist ebenfalls normalverteilt; der Erwartungswert von $B$ ist ebenso groß wie der Erwartungswert von $A,$ die Standardabweichung von $B$ ist größer als die Standardabweichung von $A.$
Skizziere in der Abbildung 2 einen möglichen Graphen der Dichtefunktion von $B.$

(2 + 3 Punkte)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

(1)

$f_{2}=x^4+(2-2)\cdot x^3-2\cdot x^2=x^4-2\cdot x^2$

Für die Symmetrie bezüglich der $y$ -Achse muss Folgendes gelten:

$\begin{array}[t]{rll} f_{2}(-x)&=&f_{2}(x) & \\[5pt] (-x)^4-2\cdot (-x)^2&=&x^4-2\cdot x^2& \\[5pt] x^4-2\cdot x^2&=&x^4-2\cdot x^2& \end{array}$

Dadurch ist $f_{2}$ symmetrisch bezüglich der $y$ -Achse.

(2)

1. Schritt: Zweite Ableitung bestimmen

Mit der Produktregel ergibt sich:

$\(f_k$

2. Schritt: Einsetzen von $x=1$

$\(\begin{array}[t]{rll} f_k$

3. Schritt: Nullstellen der zweiten Ableitung berechnen

$\(\begin{array}[t]{rll} f_k$

(1)

Mit der Produkt- und Kettenregel ergibt sich:

$\(\begin{array}[t]{rll} f_k$

(2)

1. Schritt: Notwendige Bedingung für Extremstellen anwenden

$\(\begin{array}[t]{rll} f_k$

2. Schritt: Hinreichende Bedingung für Extremstellen anwenden

$\(f_k$ für alle $k\neq 0$

Somit ist gezeigt, dass $\dfrac{1}{k^2}$ eine Extremstelle aller Funktionen dieser Schar ist.

3. Schritt: Bedingung für Minimum anwenden

$\(\begin{array}[t]{rll} f$

Daher haben alle Funktionen $f_k$ mit $k\lt0$ ein Minimum an der Stelle $x=\dfrac{1}{k^2}$ .

(1)

$\begin{array}[t]{rll} f(x)&=&h(x) &\quad \scriptsize \\[5pt] (x-3)\cdot \mathrm{e}^x&=&x-3& \mid -(x-3)\\[5pt] (x-3)\cdot \mathrm{e}^x-(x-3)&=&0& \\[5pt] (x-3)\cdot(\mathrm{e}^x-1)&=&0& \end{array}$

Mit dem Satz vom Nullprodukt folgt $x-3=0$ und $\mathrm{e}^x-1=0.$

$\begin{array}[t]{rll} x-3&=&0 &\quad \scriptsize \mid +3 \\[5pt] x&=&3& \end{array}$

$\begin{array}[t]{rll} \mathrm{e}^x-1&=&0&\quad \scriptsize \mid +1 \\[5pt] \mathrm{e}^x&=&1&\quad \scriptsize \mid \ln() \\[5pt] x&=&0& \end{array}$

Die beiden Schnittstellen der Graphen sind $x_1=3$ und $x_2=0$ .

(2)

Die Schnittstellen der beiden Funktionen geben die Intervallgrenzen an. Daher gilt für den Flächeninhalt:

Rechenweg anzeigen

$\displaystyle\int_{0}^{3}d(x)\;\mathrm dx=\mathrm{e}^3-8,5$

Der Flächeninhalt der Fläche, die von den Graphen der Funktionen $h$ und $f$ eingeschlossen ist, beträgt $\mathrm{e}^3-8,5\;\text{[FE]}$ .

(1)

Am des Funktionsgraphen von $F(x)$ können die Werte direkt abgelesen werden. Es gilt:

$\begin{array}[t]{rll} \displaystyle\int_{1}^{7}f(x)\;\mathrm dx&=& \left[F(x)\right]_1^7&\quad \scriptsize \\[5pt] &=&F(7)-F(5)& \\[5pt] &=&5-1& \\[5pt] &=&4 \;\text{[FE]}& \end{array}$

(2)

Die Ableitung $\(f$ an der Stelle $x$ ist gleich der Steigung der Funktion $f$ an der Stelle $x$ . Somit kann an den Graphen der Gunktion $F$ an der Stelle $x=1$ eine Tangente angelegt werden, deren Steigung dem Funktionswert von $f$ an dieser Stelle entspricht.

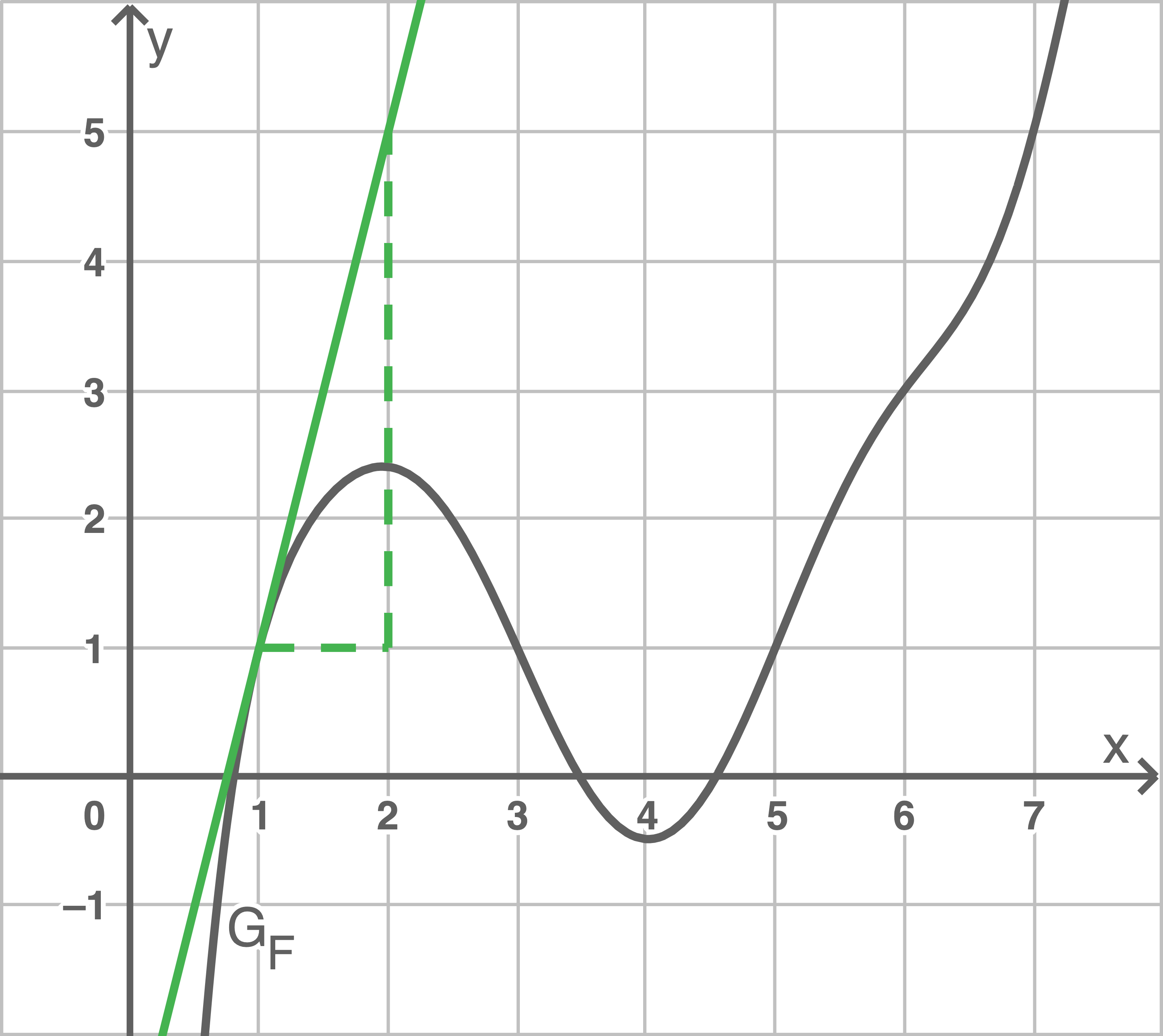Die Steigung der Tangente ergibt sich als $4$ , womit $f(1)\approx 4$ gilt.

(1)

Der Erwartungwert ergibt sich als:

$\begin{array}[t]{rll} E(X)&=&100\cdot 0,8 \\[5pt] &=&80 \end{array}$

Für die Standardabweichung gilt:

$\begin{array}[t]{rll} \sigma (X)&=&\sqrt{100 \cdot 0,8 \cdot (1-0,8)} \\[5pt] &=&4 \end{array}$

(2)

$0,8^{10} \cdot\left(\begin{array}{l}90 \\ 70\end{array}\right) \cdot 0,8^{70} \cdot 0,2^{20}$

(3)

Die Wahrscheinlichkeit für mindestens einen Treffer ist:

$\begin{array}[t]{rll} P(X\geq1)&=&P(X\geq0)-P(X=0) \\[5pt] &=&1-0,2^{100} \end{array}$

$0,2^{100}$ ist eine „sehr kleine“ positive Zahl, die nahezu den Wert Null hat.

Daher gilt:

$1-0,2^{100}\approx 1=100 \,\%$

(1)

Das Intervall $[6;10]$ ist genau mittig unter dem Graphen der Normalverteilung, womit sich die Wahrscheinlichkeit ergibt als:

$\dfrac{1-0,68}{2}=0,16=16\,\%$

(2)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?