Aufgabe 1
Die Funktion  ist gegeben durch die Gleichung
ist gegeben durch die Gleichung

 Der Graph von
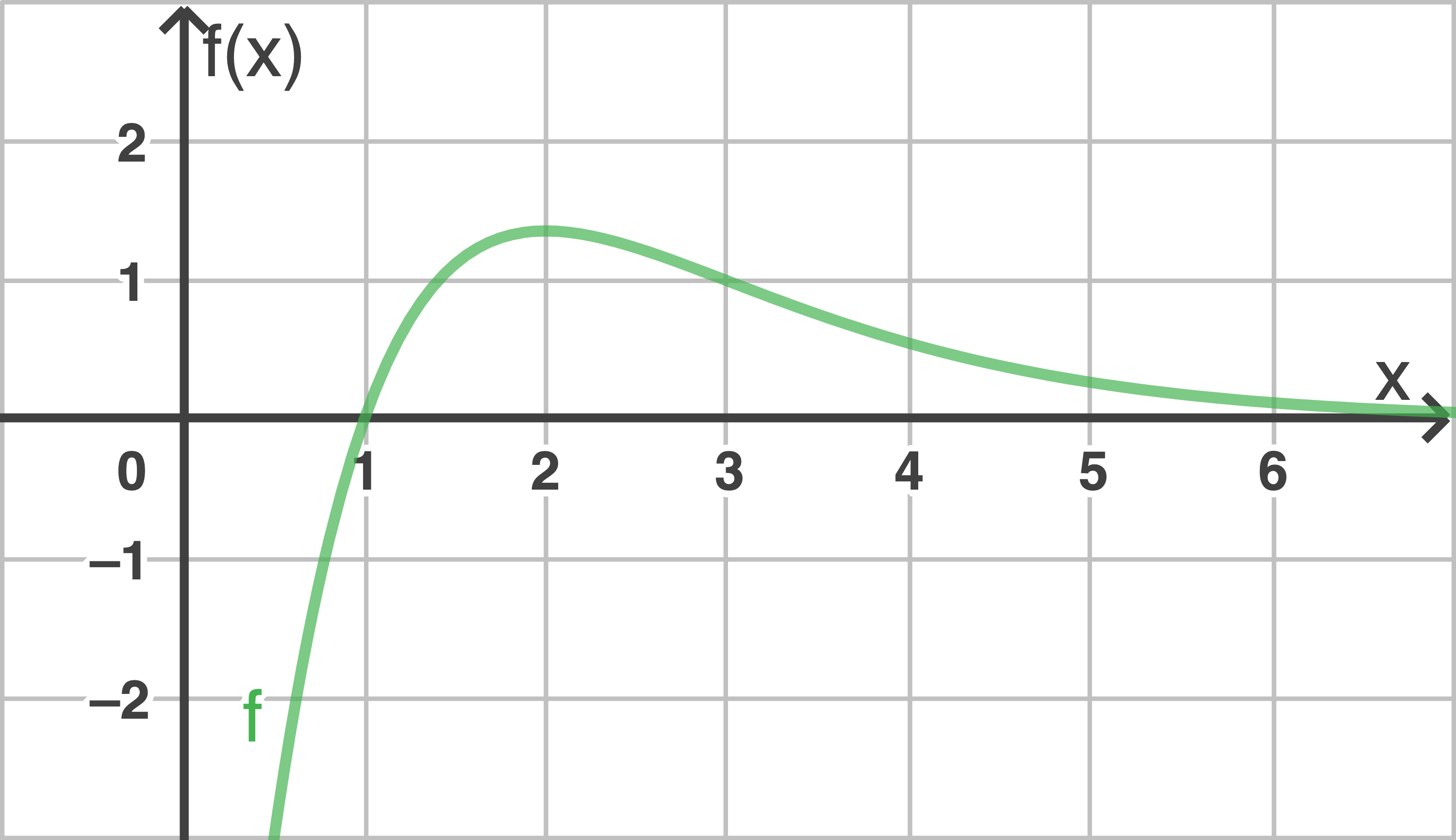
Der Graph von  ist in Abbildung 1 dargestellt.
ist in Abbildung 1 dargestellt.
 gehört zur Schar
gehört zur Schar  die gegeben ist durch
die gegeben ist durch


 Der Graph von
Der Graph von  besitzt genau einen Wendepunkt
besitzt genau einen Wendepunkt 
 ist die Tangente im Wendepunkt
ist die Tangente im Wendepunkt  Eine Gleichung für
Eine Gleichung für  ist
ist
 Für
Für  begrenzt
begrenzt  mit den beiden Koordinatenachsen ein Dreieck.
mit den beiden Koordinatenachsen ein Dreieck.
Leite einen Term für den Flächeninhalt des Dreiecks her.
des Dreiecks her.

Abbildung 1
a)
(1)
Begründe, dass  die einzige Nullstelle von
die einzige Nullstelle von  ist.
ist.
(1 P)
(2)
Untersuche  rechnerisch auf lokale Extremstellen.
rechnerisch auf lokale Extremstellen.
(3 P)
b)
(1)
Gegeben ist die Funktion  mit
mit 
 und der Wendepunkt
und der Wendepunkt  des Graphen von
des Graphen von 
Weise rechnerisch nach, dass der Graph von die Tangente an den Graphen von
die Tangente an den Graphen von  im Punkt
im Punkt  ist.
ist.
Weise rechnerisch nach, dass der Graph von
(4 P)
(2)
Die Schnittpunkte der in b) (1) gegebenen Tangente mit den beiden Koordinatenachsen legen eine Strecke fest.
Berechne die Länge dieser Strecke.
(3 P)
(3)
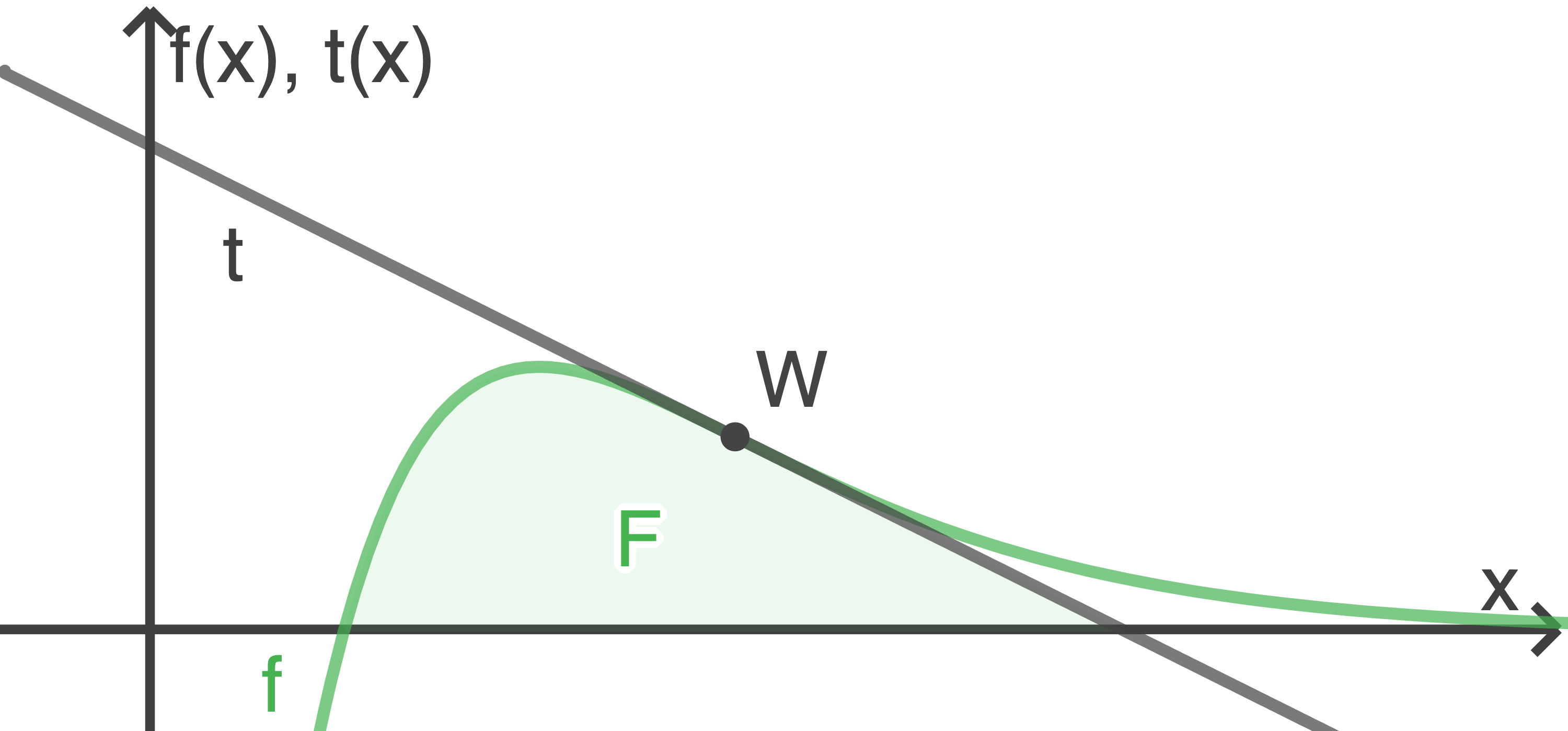
Im Intervall ![\([1;5]\)](https://mathjax.schullv.de/537aa42c72cde4f110c2f0ebdd6274a8c61a3e51c25142ee85d6d83a6bae297c?color=5a5a5a) begrenzen der Graph von
begrenzen der Graph von  und die in b) (1) gegebene Tangente zusammen mit der
und die in b) (1) gegebene Tangente zusammen mit der  -Achse eine Fläche
-Achse eine Fläche  (siehe Abbildung 2).
Bestimme den Flächeninhalt von
(siehe Abbildung 2).
Bestimme den Flächeninhalt von  auf vier Nachkommastellen gerundet.
auf vier Nachkommastellen gerundet.
(3 P)

Abbildung 2
c)
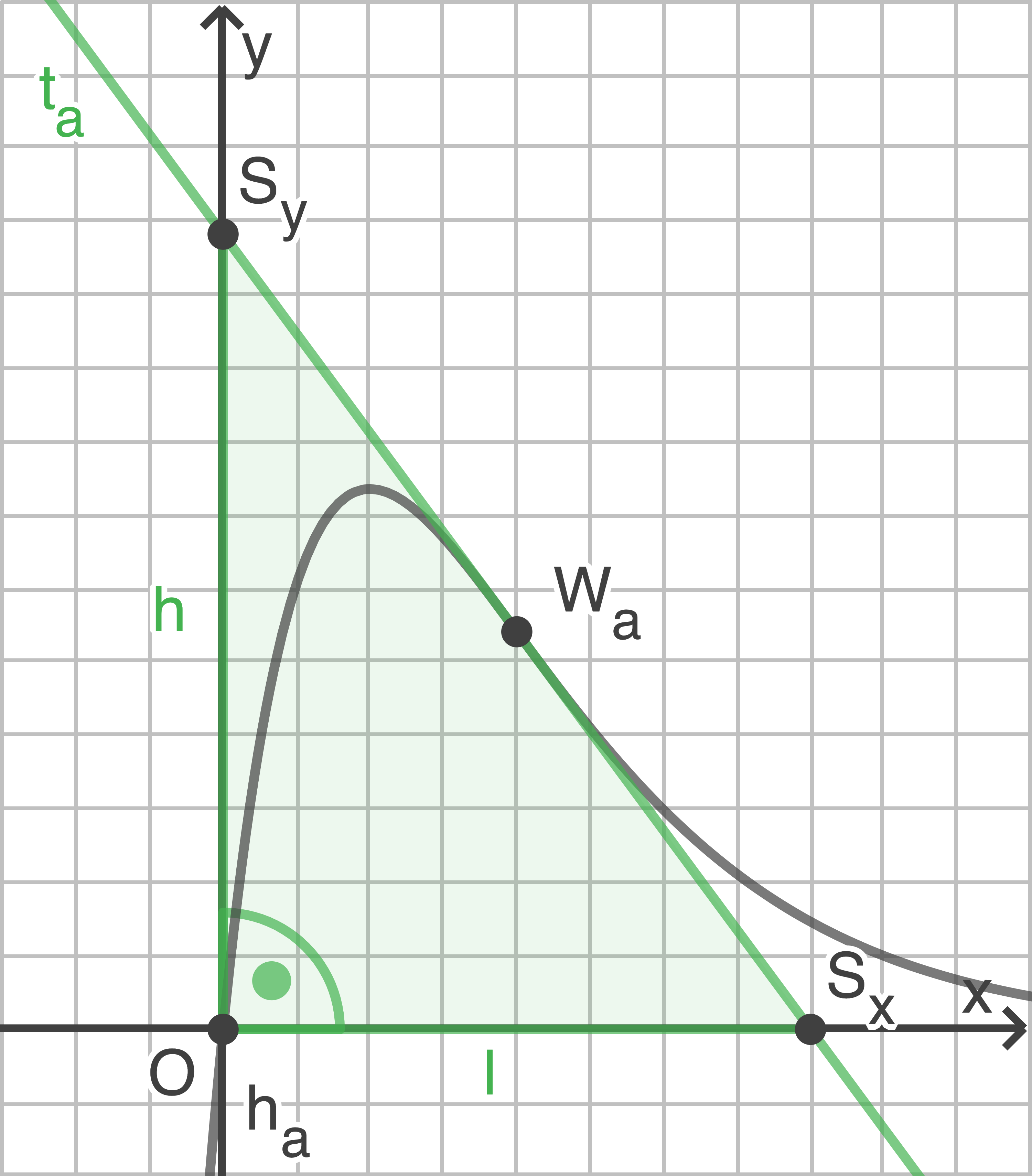
Die Gerade  ist die Parallele zur
ist die Parallele zur  -Achse durch den Hochpunkt
-Achse durch den Hochpunkt  des Graphen von
des Graphen von  Die
Die  -Achse,
-Achse,  und der Graph von
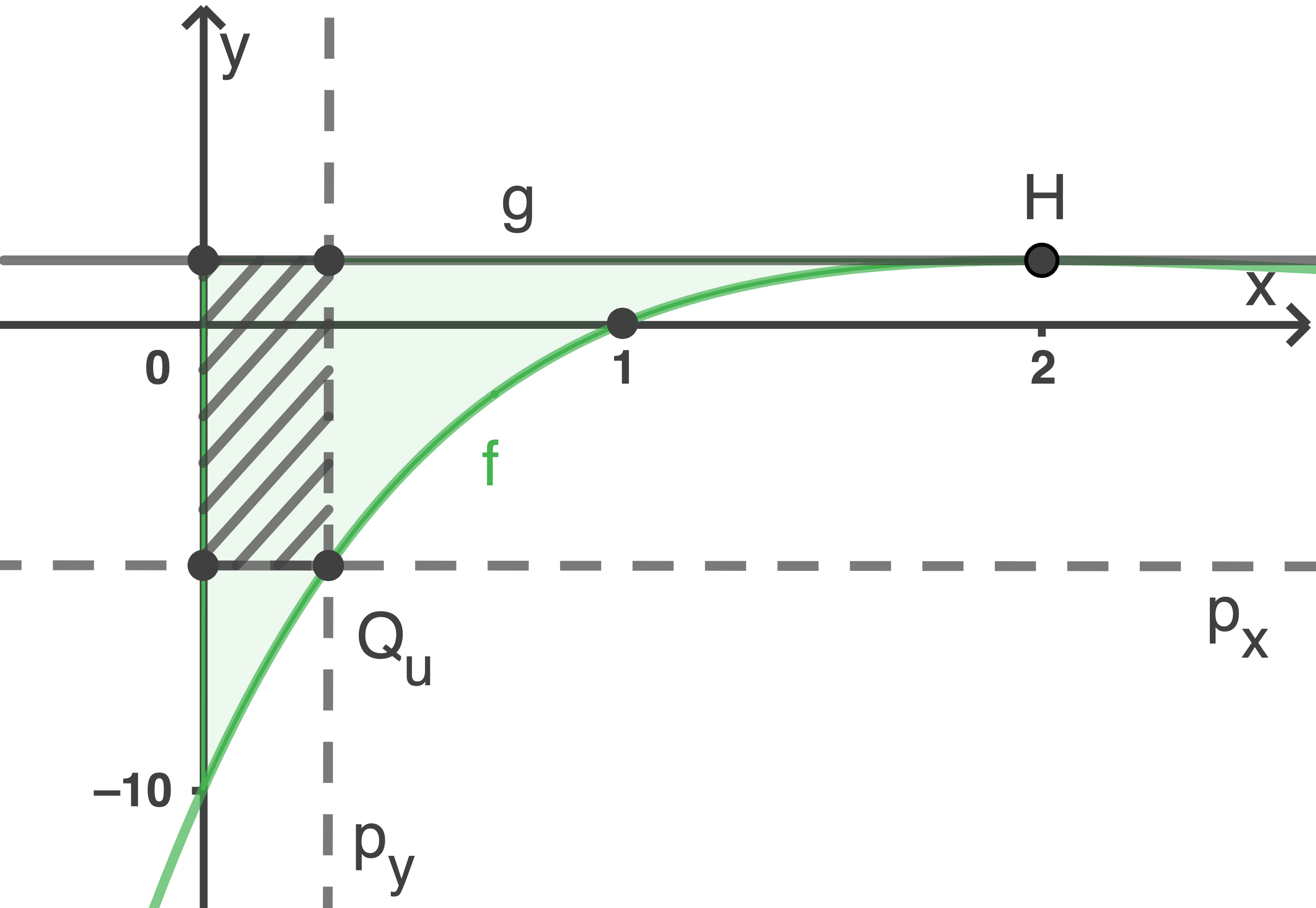
und der Graph von  schließen eine Fläche ein (siehe grün gefärbte Fläche in Abbildung 3).
schließen eine Fläche ein (siehe grün gefärbte Fläche in Abbildung 3).

 ist ein Punkt auf dem Graphen von
ist ein Punkt auf dem Graphen von  Die Parallelen durch
Die Parallelen durch  zu den beiden Koordinatenachsen werden mit
zu den beiden Koordinatenachsen werden mit  und
und  bezeichnet. Die
bezeichnet. Die  -Achse,
-Achse,  und
und  begrenzen ein Rechteck (siehe schraffierte Fläche in Abbildung 3).
begrenzen ein Rechteck (siehe schraffierte Fläche in Abbildung 3).
Die Funktion 
Abbildung 3
(1)
Ermittle den Inhalt dieser Fläche.
(3 P)
(2)
Ermittle den Flächeninhalt dieses Rechtecks für den Fall, dass  mit dem Schnittpunkt übereinstimmt, den der Graph von
mit dem Schnittpunkt übereinstimmt, den der Graph von  mit der
mit der  -Achse hat.
-Achse hat.
(2 P)
(3)
Untersuche, um wie viel Prozent sich der Wert aus (2) maximal vergrößern lässt, wenn für  eine andere Position mit
eine andere Position mit  gewählt wird.
gewählt wird.
(5 P)
d)
(1)
Ermittle die Wendestelle.
[Hinweis: Ein Nachweis der hinreichenden Bedingung ist hier nicht erforderlich.]
(3 P)
(2)
Leite einen Term für den Flächeninhalt
[Mögliche Lösung:
![\(A_D(a)=5 \cdot (a+4)^2 \cdot \mathrm e ^{-a-2}]\)](https://mathjax.schullv.de/5927c88692d2c753ccc256ce0681371628fec0349c36ff1fc08677ec3a45c16a?color=5a5a5a)
(4 P)
(3)
Ermittle einen Wert von  für den die Dreiecksfläche die Größe 10 FE hat.
für den die Dreiecksfläche die Größe 10 FE hat.
(2 P)
e)
Die Gerade  ist die Gerade, die im Wendepunkt
ist die Gerade, die im Wendepunkt  senkrecht auf der Tangente
senkrecht auf der Tangente  steht.
steht.
 ist der Schnittpunkt des Graphen von
ist der Schnittpunkt des Graphen von  mit der
mit der  -Achse.
Ermittle den Wert von
-Achse.
Ermittle den Wert von  für den die Gerade
für den die Gerade  durch
durch  verläuft.
verläuft.
(1)
Ermittle eine Gleichung für 
 Mögliche Lösung:
Mögliche Lösung:
![\(y= \dfrac{\mathrm e^{a+2}}{10} \cdot x + \dfrac{200-(a+2) \mathrm e^{2a+4}}{10 \cdot \mathrm e^{a+2}} \bigg]\)](https://mathjax.schullv.de/8d7d1a81954f1741c703349fc6502ac60cc81fc80767f0eb738a3bd9bc71326c?color=5a5a5a) [Hinweis: Ohne Nachweis kannst du den folgenden Sachverhalt nutzen:
[Hinweis: Ohne Nachweis kannst du den folgenden Sachverhalt nutzen:
Zwei Geraden stehen senkrecht aufeinander genau dann, wenn für ihre Steigungen gilt:![\(m_1 \cdot m_2 =-1.]\)](https://mathjax.schullv.de/757b23bf7fbb2e7a14e99f383bb8a36e9caf85cc30f70d963338a994f5de8b0b?color=5a5a5a)
Zwei Geraden stehen senkrecht aufeinander genau dann, wenn für ihre Steigungen gilt:
(4 P)
(2)
(4 P)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
(1)
(2)
1. Schritt: Die ersten beiden Ableitungen bilden
Mit der Produktregel folgt:
![\(\begin{array}[t]{rlll}
f](https://mathjax.schullv.de/23f9d8bfac9f1131af6c84921a265682162d54dcbdef6d2afe992eb2690ed158?color=5a5a5a) Erneutes Anwenden der Produktregel:
2. Schritt: Notwendige Bedingung für Extremstellen anwenden
Erneutes Anwenden der Produktregel:
2. Schritt: Notwendige Bedingung für Extremstellen anwenden
![\(\begin{array}[t]{rlll}
f](https://mathjax.schullv.de/4379addb69991d87c53fa2e00bf50165fcd29efc0bf304b470f5e0306e1ed02b?color=5a5a5a) Da
Da  und
und  für alle
für alle  folgt mit dem Satz vom Nullprodukt, dass
folgt mit dem Satz vom Nullprodukt, dass  sein muss und daraus folgt
sein muss und daraus folgt  als einzige lokale Extremstelle.
3. Schritt: Hinreichende Bedingung für Extremstellen anwenden
als einzige lokale Extremstelle.
3. Schritt: Hinreichende Bedingung für Extremstellen anwenden

 Also besitzt
Also besitzt  genau eine lokale Extremstelle: Bei
genau eine lokale Extremstelle: Bei  nimmt
nimmt  ein lokales Maximum an.
ein lokales Maximum an.
b)
(1)
Es muss geprüft werden, ob die Graphen von  und
und  an der Stelle
an der Stelle  die gleiche Steigung haben und ob der Punkt
die gleiche Steigung haben und ob der Punkt  auf dem Graphen von
auf dem Graphen von  liegt.
1. Schritt: Steigung prüfen
Die Steigung von
liegt.
1. Schritt: Steigung prüfen
Die Steigung von  lässt sich aus der Geradengleichung ablesen mit
lässt sich aus der Geradengleichung ablesen mit  Für die Steigung des Graphen von
Für die Steigung des Graphen von  an der Stelle
an der Stelle  ergibt sich mit der ersten Ableitung:
ergibt sich mit der ersten Ableitung:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/23a295525389f38d11f348744e1ed6bae8be06089788daeece8b93e5e4b572be?color=5a5a5a) Die Gerade
Die Gerade  hat die gleiche Steigung wie der Graph von
hat die gleiche Steigung wie der Graph von  an der Stelle
an der Stelle  2. Schritt: Prüfen, ob der Punkt
2. Schritt: Prüfen, ob der Punkt  auf der Tangente
auf der Tangente  liegt
Es gilt:
liegt
Es gilt: 

![\(\begin{array}[t]{rlll}
t(3) & = & -10\cdot\mathrm e^{-3}\cdot 3+50\cdot \mathrm e^{-3} \\[5pt]
&= & 20 \cdot\mathrm e^{-3} \\[5pt]
&=& f(3) \\[5pt]
\end{array}\)](https://mathjax.schullv.de/6ea6ee36abbbe0f07df153ba505596ed6321d2b831f290e95b024f1fd53375f1?color=5a5a5a)
 ist ein gemeinsamer Punkt der Graphen von
ist ein gemeinsamer Punkt der Graphen von  und
und 
Damit ist der Graph von die Tangente an den Graphen von
die Tangente an den Graphen von  im Punkt
im Punkt 
Damit ist der Graph von
(2)
1. Schnittpunkte der Tangente mit den Koordinatenachsen bestimmen
Somit folgt der Schnittpunkt mit der  -Achse
-Achse 
![\(\begin{array}[t]{rlll}
t(0) &=& -10\cdot \mathrm e^{-0}\cdot0+50 \cdot \mathrm e^{-3} \\[5pt]
&=& 50 \cdot \mathrm e^{-3}& \quad \scriptsize\\[5pt]
\end{array}\)](https://mathjax.schullv.de/fa260c3ade4d7e64f0fea6565dc580b200a6e0b43441891f6d7b4d217adb151a?color=5a5a5a) Der Schnittpunkt der Tangente mit der
Der Schnittpunkt der Tangente mit der  -Achse ist
-Achse ist  2. Länge der Strecke zwischen den Schnittpunkten bestimmen
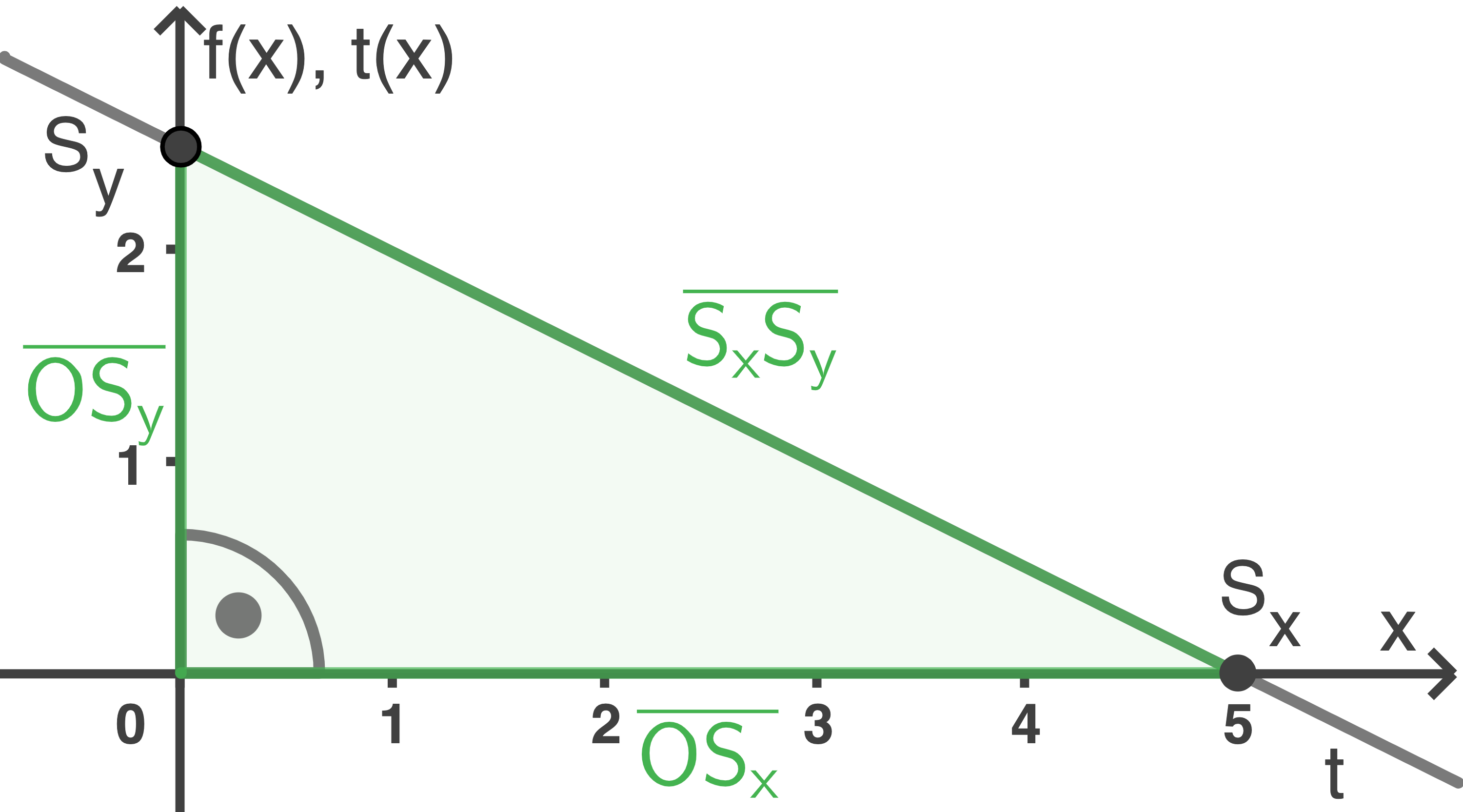
2. Länge der Strecke zwischen den Schnittpunkten bestimmen
![\(\begin{array}[t]{rlll}
\mid \overline{S_xS_y}\mid^2 &=& 5^2+(50 \cdot \mathrm e^{-3})^2& \quad \scriptsize \mid \; \sqrt{\;}\\[5pt]
\mid \overline{S_xS_y}\mid &=& \sqrt{ 5^2+ (-50 \cdot \mathrm e^{-3})^2}\\[5pt]
&\approx& 5,5854& \quad \scriptsize\\[5pt]
\end{array}\)](https://mathjax.schullv.de/bc6c89d7bb7728158d7b6ba9f97a8663d17b05fab7c29a5cd2e5cba23aadde02?color=5a5a5a) Die Länge der Strecke zwischen den Schnittpunkten der Tangente mit den Koordinatenachsen beträgt
Die Länge der Strecke zwischen den Schnittpunkten der Tangente mit den Koordinatenachsen beträgt ![\(5,5854 \; [\text{LE}].\)](https://mathjax.schullv.de/306f095d07528ad389eeaf3999feb3185141064b41f3d2faa1b0d32e6e42b5f3?color=5a5a5a)
Die Länge der Strecke zwischen den Schnittpunkten wird mit dem Satz des Pythagoras bestimmt, da  ein rechtwinkliges Dreieck mit der Hypotenuse
ein rechtwinkliges Dreieck mit der Hypotenuse  ist.
ist.

(3)
Für den Inhalt der Fläche  gilt:
gilt: 


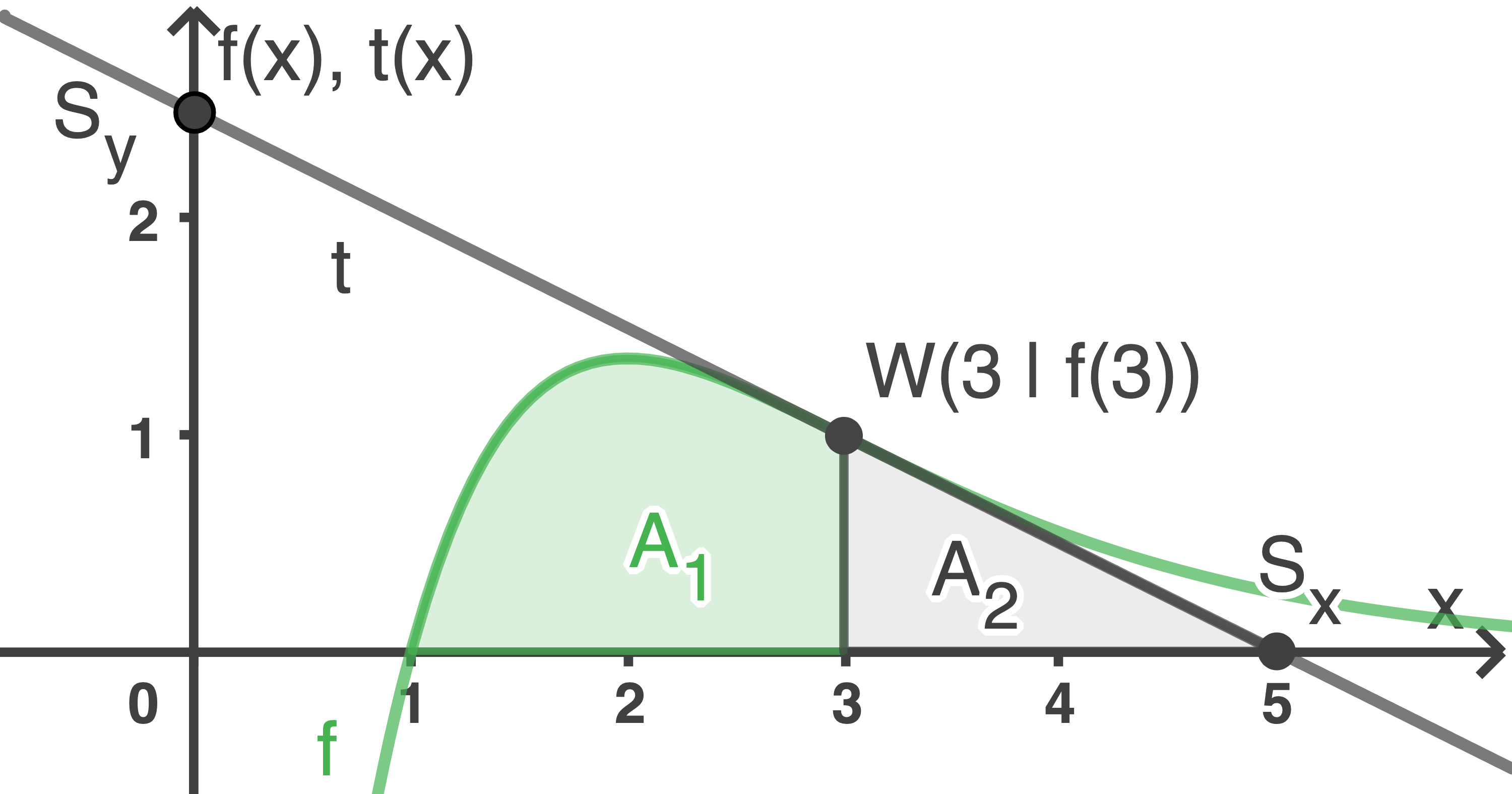
Die Integrationsgrenzen ergeben sich in den vorherigen Teilaufgaben und werden mithilfe der Abbildung nochmal deutlich. Die Werte von
menu  4: Analysis
4: Analysis  3: Integral
3: Integral
keyboard  Math2
Math2 

c)
(1)
1. Schritt: Geradengleichung  ermitteln
Es gilt:
ermitteln
Es gilt:  Da
Da  parallel zur
parallel zur  -Achse ist, folgt die Gleichung mit
-Achse ist, folgt die Gleichung mit  2. Schritt: Inhalt der Fläche bestimmen
2. Schritt: Inhalt der Fläche bestimmen
Der Flächeninhalt der eingeschlossenen Fläche entspricht dem Wert welcher mit dem CAS berechnet wird.
welcher mit dem CAS berechnet wird.
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Der gesuchte Flächeninhalt folgt mit
Casio Classpad II
Der gesuchte Flächeninhalt folgt mit ![\(\displaystyle\int_{0}^{2}g-f(x)\;\mathrm dx \approx 5,4134 \; [\text{FE}].\)](https://mathjax.schullv.de/799a19e1ded909b1fca7d08696515adfa09f8e7294982bd5f91a023279d11a33?color=5a5a5a)
Der Flächeninhalt der eingeschlossenen Fläche entspricht dem Wert
menu  4: Analysis
4: Analysis  3: Integral
3: Integral
keyboard  Math2
Math2 

(2)
1. Schritt: Koordinaten von  Der Abbildung in der Aufgabenstellung kann entnommen werden, dass der Graph von
Der Abbildung in der Aufgabenstellung kann entnommen werden, dass der Graph von  die
die  -Achse an der Stelle
-Achse an der Stelle  schneidet. Damit folgt
schneidet. Damit folgt  und das in der Abbildung dargestellte Rechteck.
und das in der Abbildung dargestellte Rechteck.

(3)
1. Schritt: Allgemeine Funktionsgleichung  zur Berechnung des Flächeninhalts aufstellen
Mit der
zur Berechnung des Flächeninhalts aufstellen
Mit der  - Koordinate von
- Koordinate von  ergibt sich die Länge des Rechtecks mit
ergibt sich die Länge des Rechtecks mit  Die Breite des Rechtecks entspricht dem
Die Breite des Rechtecks entspricht dem  -Achsenabschnitt der Geraden
-Achsenabschnitt der Geraden  abzüglich der
abzüglich der  -Koordinate von
-Koordinate von  mit
mit  Der Flächeninhalt kann für jede Postion von
Der Flächeninhalt kann für jede Postion von  für
für  mit
mit  bestimmt werden.
2. Den maximalen Flächeninhalt bestimmen
Durch eine graphische Analyse mit dem CAS wird das Maximum von
bestimmt werden.
2. Den maximalen Flächeninhalt bestimmen
Durch eine graphische Analyse mit dem CAS wird das Maximum von  bestimmt.
bestimmt.
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Der Flächeninhalt wird für
Casio Classpad II
Der Flächeninhalt wird für ![\(u \approx 0,485 \; [\text{LE}]\)](https://mathjax.schullv.de/0a5f7a65a43934817f35d3cbeb9efc81a8a79dd700e65e702e2bf3c3749d3543?color=5a5a5a) mit
mit ![\(A(u)=2,1942\; [\text{FE}]\)](https://mathjax.schullv.de/2aba445e669572aae25bb91cd9c3ba3090f945f29cc262bc60e386e0792e2d53?color=5a5a5a) maximal.
3. Prozentuale Vergrößerung
Es gilt
maximal.
3. Prozentuale Vergrößerung
Es gilt ![\(A_R=1,3534 \; [\text{FE}]\)](https://mathjax.schullv.de/901c6ff10d1ac35303f924601bdbf5fb0234c9caff9b61df20f9dd0542e39d75?color=5a5a5a) (aus (2)) und
(aus (2)) und ![\(A(u)=2,1942\; [\text{FE}].\)](https://mathjax.schullv.de/fe4ce70c02be6bc697f2cea2becb7ff1a3f3045d921a69975343ec72aee3ad58?color=5a5a5a)
![\(\dfrac{2,1942\; [\text{FE}]}{1,3534 \; [\text{FE}]} \approx 1,623\)](https://mathjax.schullv.de/05647a9e8233eca049f4661c98ab9f872ec70a141ec11e14e5dee9f79c48ae0b?color=5a5a5a) Der Flächeninhalt kann maximal um ca.
Der Flächeninhalt kann maximal um ca.  % vergrößert werden.
% vergrößert werden.
menu  6: Graph analysieren
6: Graph analysieren  3: Maximum
3: Maximum
Analyse  Grafische Lösung
Grafische Lösung  Maximum
Maximum
d)
(1)
Notwendige Bedingung für Wendestellen
![\(\begin{array}[t]{rlll}
h](https://mathjax.schullv.de/b8fe4f76da8c647b5f606d9d43e048abe7c750c2d9346e9f34befe1d568251d6?color=5a5a5a) Da
Da  und
und  muss mit dem Satz vom Nullprodukt
muss mit dem Satz vom Nullprodukt  sein. Daraus folgt
sein. Daraus folgt  Auf die hinreichende Bedingung für Extremstellen kann verzichtet werden und somit ergibt sich genau eine Wendestelle.
Auf die hinreichende Bedingung für Extremstellen kann verzichtet werden und somit ergibt sich genau eine Wendestelle.
(2)
Das Dreieck, welches  mit den Koordinatenachsen begrenzt, hat einen rechten Winkel im Ursprung. Der Flächeninhalt des Dreiecks folgt mit
mit den Koordinatenachsen begrenzt, hat einen rechten Winkel im Ursprung. Der Flächeninhalt des Dreiecks folgt mit  Um
Um  und
und  zu bestimmen, müssen die Schnittpunkte mit den Koordinatenachsen bestimmt werden.
zu bestimmen, müssen die Schnittpunkte mit den Koordinatenachsen bestimmt werden.
(3)
e)
(1)
Die Gleichung der Geraden  ist gegeben durch
ist gegeben durch  1. Schritt: Steigung der Geraden
1. Schritt: Steigung der Geraden  bestimmen
Es gilt
bestimmen
Es gilt  , die Steigung der Tangente ist gegeben durch
, die Steigung der Tangente ist gegeben durch  und daraus folgt:
2. Schritt: Den
und daraus folgt:
2. Schritt: Den  -Achsenabschnitt
-Achsenabschnitt  bestimmen
Die Koordinaten des Wendepunkts
bestimmen
Die Koordinaten des Wendepunkts  und die Steigung
und die Steigung  werden in
werden in  eingesetzt.
Eine Gleichung für
eingesetzt.
Eine Gleichung für  ist somit
ist somit 
(2)
1. Schritt: Schnittstellen von  und
und  mit der
mit der  -Achse
Die Schnittstelle von
-Achse
Die Schnittstelle von  mit der
mit der  -Achse ergibt sich mit dem solve-Befehl des CAS für
-Achse ergibt sich mit dem solve-Befehl des CAS für  und folgt mit
und folgt mit  Die Schnittstelle von
Die Schnittstelle von  mit der
mit der  -Achse folgt mit
-Achse folgt mit  Da
Da  und
und  folgt mit dem Satz vom Nullprodukt
folgt mit dem Satz vom Nullprodukt  und daraus die Schnittstelle an
und daraus die Schnittstelle an  Die Koordinaten von
Die Koordinaten von  folgen mit
folgen mit  .
2. Schritt: Wert von
.
2. Schritt: Wert von  ermitteln
Gleichsetzen der Schnittstellen ergibt:
ermitteln
Gleichsetzen der Schnittstellen ergibt:
 Mit dem solve-Befehl des CAS ergibt sich der Wert für
Mit dem solve-Befehl des CAS ergibt sich der Wert für  mit
mit 