Aufgabe 1

Die Zahl der Haushalte in Deutschland, die über einen Glasfaseranschluss erreichbar sind, wächst ständig. Aber nicht alle erreichbaren Haushalte nutzen auch ihre Anschlüsse.

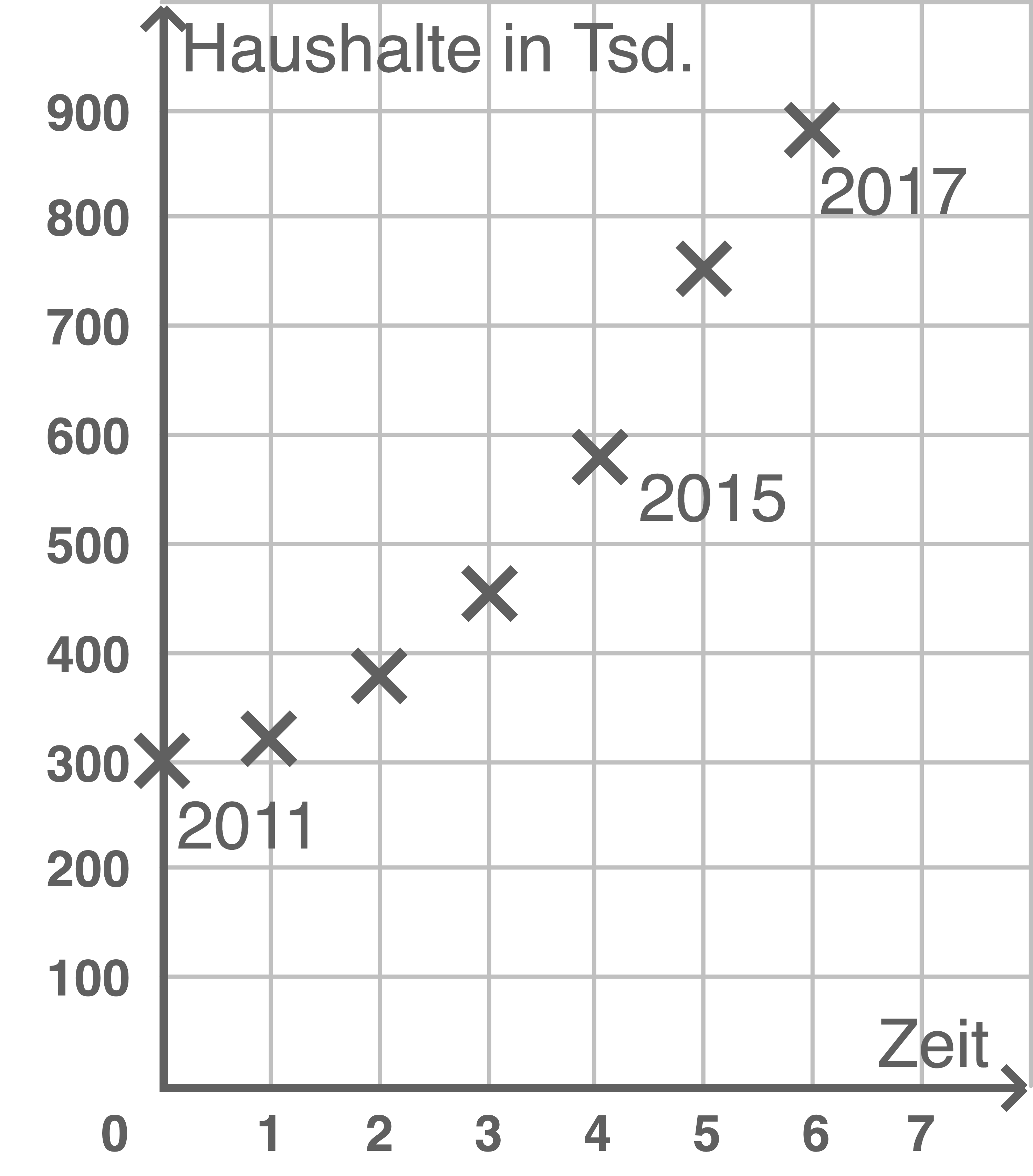
Die Abbildung zeigt die Anzahl der Haushalte mit genutztem Glasfaseranschluss (im Folgenden Glasfaserhaushalte genannt) für die Jahre 2011 bis 2017. Dabei wird auf der $t$ -Achse die Zeit in Jahren seit dem 01.01.2011 und auf der $y$ -Achse die Anzahl der Glasfaserhaushalte in Tausend angegeben.

nrw abi gk gtr 2019 teil b aufgabe 1 abbildung 1 glasfaseranschluss statistik

Die Anzahl der Glasfaserhaushalte in Tausend wird durch eine Exponentialfunktion $f$ der Form $f(t)=a \cdot \mathrm e^{b \cdot t}$ modelliert, deren Graph durch die Punkte $P_1(0 \mid 296)$ und $P_2(4 \mid 590)$ verläuft. Diese Funktion soll für Prognosen bis zum Jahr 2026 $(t=15)$ genutzt werden.

(1)

Gib den Parameter $a$ an und bestimme $b$ auf drei Nachkommastellen genau.

Im Folgenden soll mit $f(t)=296 \cdot \mathrm e^{0,17 \cdot t}$ weitergearbeitet werden.

(2)

Im Jahr 2017 wurden in einer Erhebung ca. $880.000$ Glasfaserhaushalte gezählt.
Bestimme die sinnvoll gerundete Anzahl der Glasfaserhaushalte, die sich bei der Modellierung mit der Funktion $f$ für den 01.01.2017 ergibt.
Ermittle die prozentuale Abweichung zu dem Wert aus der Erhebung.

(3)

Bestimme im Modell für $0 \leq t \leq 15$ den Zeitpunkt, zu dem die Anzahl der Glasfaserhaushalte am schnellsten wächst.
Bestimme die zugehörige Wachstumsgeschwindigkeit und gib die Einheit an.

(4 + 4 + 5 Punkte)

Es wird prognostiziert, dass der Markt für Glasfaseranschlüsse im weiteren Verlauf in eine Sättigungsphase eintritt, da eine zunehmende Zahl von Haushalten bereits über einen Glasfaseranschluss verfügt. Im Folgenden wird die Funktion $f$ nur zur Prognose der Anzahl von Glasfaserhaushalten in Tausend bis zum 01.01.2026 $(t \leq 15)$ genutzt. Der momentane Zuwachs der Anzahl der Glasfaserhaushalte in Tausend pro Jahr ab dem 01.01.2026 $(t \geq 15)$ wird durch die Änderungsrate $z$ mit der Funktionsgleichung $z(t)=50,32 \cdot \mathrm e^{6,99-0,296 \cdot t}$ modelliert.

(1)

Es gilt: $z(t)\gt 0$ und $\(z$ für alle $t\in\mathbb{R}.$

[Ein Nachweis ist nicht erforderlich.]

Interpretiere diese Aussage für $t\geq 15$ im Sachzusammenhang.

(2)

Bestimme die Anzahl der Glasfaserhaushalte, die gemäß der Modellierung von 01.01.2026 bis zum 01.01.2036 hinzukommen.

(3)

Gib einen Ansatz für einen Funktionsterm einer Funktion $h$ an, der für $t\geq15$ die Anzahl der Glasfaserhaushalte in Tausend modelliert. Eine Vereinfachung oder Berechnung ist nicht erforderlich.

(4 + 4 + 4 Punkte)

Bei vielen Technologien nimmt die Anzahl der Nutzer aufgrund des technischen Fortschritts mit der Zeit wieder ab. Um auch diesen Aspekt zu erfassen, wird für $t\geq 15$ eine alternative Modellierung genutzt. Die Funktion $k_a$ mit der Funktionsgleichung

$k_a(t)=296 ...$

Funktion anzeigen

modelliert im Folgenden die Anzahl der Glasfaserhaushalte in Tausend für $t \geq 15.$

(1)

Weise nach, dass für $t=15$ die Änderungsrate der Funktion $k_a$ unabhängig vom Parameter $a$ mit der Änderungsrate der Funktion $f$ übereinstimmt.

[Zur Kontrolle: $\(k_a{}$ ]

(2)

Die Funktion $k_a$ besitzt ein lokales Maximum $H_a.$
Bestimme das lokale Maximum $H_a$ der Funktion $k_a$ in Abhängigkeit von $a.$

Hinweis: Auf den Nachweis einer hinreichenden Bedingung kann verzichtet werden.

Alle Hochpunkte $H_a\left(15+ \dfrac {1} {a} \,\bigg \vert \, k_a \left(15+ \dfrac {1} {a}\right)\right)$ der Funktionenschar $k_a$ liegen auf dem Graphen der Funktion $g$ mit $g(t)\approx 237,08 t +234,69.$ [Ein Nachweis ist nicht erforderlich.]

(3)

Um den Sachverhalt angemessen zu modellieren, soll der Wertebereich für den Parameter $a$ weiter eingegrenzt werden.
Bestimme den Wertebereich für den Parameter $a$ so, dass die maximale Anzahl der Glasfaserhaushalte zwischen fünf und sechs Millionen liegt.

(5 + 5 + 4 Punkte)

(1)

Für große Werte von $t$ nähert sich der Graph von $z$ einem Wert an.
Gib diesen Wert begründet an.

(2)

Bestimme die Anzahl der Glasfaserhaushalte, die gemäß der Modellierung von 01.01.2026 bis zum 01.01.2036 hinzukommen.

(3)

Gib einen Ansatz für einen Funktionsterm einer Funktion $h$ an, der für $t\geq15$ die Anzahl der Glasfaserhaushalte in Tausend modelliert. Eine Vereinfachung oder Berechnung ist nicht erforderlich.

(4)

Es gilt: $z(t)\gt 0$ und $z‘(t)\lt 0$ für alle $t\in\mathbb{R}.$ [Ein Nachweis ist nicht erforderlich.]

Interpretiere diese Aussage für $t\geq 15$ im Sachzusammenhang.

(3 + 4 + 4 + 4 Punkte)

Bei vielen Technologien nimmt die Anzahl der Nutzer aufgrund des technischen Fortschritts mit der Zeit wieder ab. Um auch diesen Anspekt zu erfassen, wird für $t\geq 15$ eine alternative Modellierung genutzt. Die Funktion $k_a$ mit der Funktionsgleichung

$k_a(t)=296...$

Funktion anzeigen

modelliert im Folgenden die Anzahl der Glasfaserhaushalte in Tausend für $t \geq 15.$

(1)

Weise nach, dass für $t=15$ die Änderungsrate der Funktion $k_a$ unabhängig vom Parameter $a$ mit der Änderungsrate der Funktion $f$ übereinstimmt.

(2)

Weise nach, dass die Funktion $k_a$ ein lokales Maximum $H_a$ in Abhängigkeit von $a$ besitzt und gib dieses an.

Alle Hochpunkte $H_a\left(15+ \frac {1} {a} \mid k_a \left(15+ \frac{1}{a}\right)\right)$ der Funktionenschar $k_a$ liegen auf dem Graphen der Funktion $g$ mit $g(t)\approx 237,08 t +234,69$ . [Ein Nachweis ist nicht erforderlich.]

(3)

(3 + 5 + 4 Punkte)

(1)

Einsetzen der Koordinaten von $P_1$ in die Funktionsgleichung:

$\begin{array}[t]{rll} f(t) &=& a\cdot \mathrm e^{b\cdot t} \\[5pt] 296 &=& a\cdot \mathrm e^{b\cdot 0} \\[5pt] 296 &=& a\cdot 1\\[5pt] 296 &=& a \\[5pt] \end{array}$

Einsetzen der Koordinaten von $P_2$ liefert eine Gleichung für $b,$ die mit dem solve-Befehl des CAS gelöst wird:

$\begin{array}[t]{rll} f(t) &=& a\cdot \mathrm e^{b\cdot t} \\[5pt] f(t) &=& 296 \cdot \mathrm e^{b\cdot t} \\[5pt] 590 &=& 296 \cdot \mathrm e^{b\cdot 4} \\[5pt] 0,172 &\approx& b \end{array}$

(2)

$\begin{array}[t]{rll} f(6) &=& 296\cdot \mathrm e^{0,17\cdot 6} \\[5pt] &\approx& 820,866 \end{array}$

Für den 01.01.2017 ergibt sich mit Hilfe der Modellierung mit der Funktion $f$ eine Anzahl von ca. $820\,000$ Glasfaserhaushalten.

Mit der Abbildung ergeben sich für den 01.01.2017 ca. $880\,000$ Glasfaserhaushalte aus der Erhebung.

$\dfrac{820\,000}{880\,000} \approx 0,932$

Der Wert, der sich aus der Modellierung mit der Funktion $f$ ergibt, weicht um ca. $6,8\,\%$ von dem Wert aus der Erhebung ab.

(3)

Gesucht ist das Maximum von $\(f$ für $0\leq t \leq 15.$

1. Schritt: Ableitungsfunktion bestimmen

$\(\begin{array}[t]{rll} f(t) &=& 296\cdot \mathrm e^{0,17\cdot t} \\[10pt] f$

2. Schritt: Maximum bestimmen

$\blacktriangleright$ TI nspire CAS

Mit dem fMax-Befehl ergibt sich die Stelle $t\in[0;15],$ an der der Funktionswert von $f$ am größten ist.

$\text{fMax(f(t),t,0,15)}$

$t_{\text{max}} = 15$

Der zugehörige Funktionswert lässt sich ebenfalls mit dem CAS berechnen:

$\begin{array}[t]{lll} f(15) &\approx & 644,45\\[5pt] \end{array}$

$\blacktriangleright$ Casio Classpad II

Mit dem fMax-Befehl ergibt sich der größte Funktionswert von $f$ im angegebenen Intervall und die zugehörige Stelle $t_{\text{max}}$ .

$\text{fMax(f(t),t,0,15)}$

$\begin{array}[t]{rll} f(t_{\text{max}})&\approx& 644,45\\[5pt] \end{array}$

$t_{\text{max}} =15$

Die Anzahl der Glasfaserhaushalte wächst nach $15$ Jahren am schnellsten. Zu diesem Zeitpunkt wächst sie mit einer Geschwindigkeit von ca. $640\,000$ Haushalten pro Jahr.

(1)

Für große Werte von $t$ gilt für den Exponenten $(6,99-0,296\cdot t) \to -\infty.$ Für $\mathrm e^x$ und $x\to -\infty$ gilt $\mathrm e^x \to 0.$ Damit gilt also insgesamt $\mathrm e^{6,99-0,296\cdot t }\to 0.$ Der Graph von $z$ nähert sich für große Werte von $t$ also Null an.

(2)

Integrale werden mit Hilfe des CAS berechnet:

$\blacktriangleright$ TI nspire CAS

menu $\to$ 4: Analysis $\to$ 3: Integral

$\blacktriangleright$ Casio Classpad II

keyboard $\to$ Math2 $\to$ $\int_{\Box}^{\Box}\Box$

$\displaystyle\int_{15}^{25}z(t)\;\mathrm dt\approx 2\,064,39$

Vom 01.01.2016 bis zum 01.01.2036 kommen gemäß der Modellierung mit $z$ ca. $2\,060\,000$ Glasfaserhaushalte hinzu.

(3)

Mit $f(15)$ wird die Anzahl der Glasfaserhaushalte für $t=15$ beschrieben. Mit $\displaystyle\int_{15}^{t}z(x)\;\mathrm dx$ lässt sich in Abhängigkeit von $t\geq 15$ die Anzahl der hinzugekommenen Haushalte seit $t=15$ beschreiben.

$h(t) =...$

Vollständige Lösung anzeigen

(4)

$z$ beschreibt die Wachstumgsgeschwindigkeit der Anzahl der Glasfaserhaushalte, $z‘$ beschreibt die Zu-/Abnahme der Wachstumsgeschwindigkeit.

Da $z(t)\gt 0$ ist, wächst die Anzahl der Glasfaserhaushalte im Modell ab $t=15$ weiterhin. Wegen $z‘(t) \lt 0$ wächst die Anzahl der Glasfaserhaushalte in diesem Zeitraum aber immer langsamer.

(1)

$\begin{array}[t]{rll} k_a(t) &=& 296\cdot \mathrm e^{2,55} + 50,32(t-15)\cdot \mathrm e^{2,55-a\cdot (t-15)} \\[5pt] k_a‘(t) &=& 50,32\left( 1\cdot \mathrm e^{2,55-a\cdot (t-15)} +(t-15)\cdot (-a)\cdot \mathrm e^{2,55-a\cdot (t-15)} \right) \\[5pt] &=& 50,32\cdot \mathrm e^{2,55-a\cdot (t-15)}\cdot \left( 1 +(t-15)\cdot (-a) \right) \\[10pt] k_a‘(15)&=& 50,32\cdot \mathrm e^{2,55-a\cdot (15-15)}\cdot \left( 1 +(15-15)\cdot (-a) \right) \\[5pt] &=& 50,32\cdot \mathrm e^{2,55} \\[10pt] f‘(15) &=& 50,32\cdot \mathrm e^{0,17\cdot 15} \\[5pt] &=& 50,32\cdot \mathrm e^{2,55} \end{array}$

Es ist also $\(k_a$ unabhängig von $a.$

(2)

1. Schritt: Notwendiges Kriterium für Extremstellen anwenden

$\begin{array}[t]{rll} k_a‘(t) &=& 0 \\[5pt] 50,32\cdot \mathrm e^{2,55-a\cdot (t-15)}\cdot \left( 1 +(t-15)\cdot (-a) \right) &=& 0 &\quad \scriptsize \mid\;:50,32 \\[5pt] \mathrm e^{2,55-a\cdot (t-15)}\cdot \left( 1 +(t-15)\cdot (-a) \right) &=& 0 &\quad \scriptsize \mid\; :\mathrm e^{2,55-a\cdot (t-15)} \\[5pt] 1 +(t-15)\cdot (-a) &=& 0 &\quad \scriptsize \mid\;-1 \\[5pt] (t-15)\cdot (-a) &=& -1 &\quad \scriptsize \mid\;:(-a) \\[5pt] t-15 &=& \frac{1}{a} &\quad \scriptsize \mid\; +15 \\[5pt] t &=& \frac{1}{a} +15 \end{array}$

2. Schritt: Hinreichendes Kriterium überprüfen

$\(\begin{array}[t]{rll} k_a$

An der Stelle $t=\frac{1}{a} +15$ besitzt $k_a$ also ein lokales Maximum.

3. Schritt: Maximum berechnen

$k_a\left( \frac{1}{a} +15 \right) = ...$

Vollständige Lösung anzeigen

Das lokale Maximum der Funktion $k_a$ liegt bei

$H_a\left( \frac{1}{a} +15 \mid 296\cdot \mathrm e^{2,55} +\frac{50,32}{a}\cdot \mathrm e^{1,55} \right).$

(3)

Alle Hochpunkte $H_a$ liegen auf dem Graphen der Funktion $g.$ Dabei handelt es sich um eine streng monoton steigende Gerade.

Die Grenzen $a_1$ und $a_2$ des Wertebereichs müssen daher folgende Gleichungen erfüllen, die jeweils mit dem solve-Befehl des CAS lösbar sind:

$\begin{array}[t]{lrll} \text{I}\quad & g\left(\frac{1}{a_1}+15 \right)&=& 5\,000 \\[5pt] & a_1 &\approx& 0,196 \\[10pt] \text{II}\quad & g\left(\frac{1}{a_2}+15 \right)&=& 6\,000 \\[5pt] & a_2 &\approx& 0,107 \\[10pt] \end{array}$

Der Wertebereich für den Parameter $a$ lautet $\text{W}=[0,107;0,196].$