Aufgabe 2

Für jede reelle Zahl $k \geq 0$ ist durch die Gleichung

$f_k(x) = x^3-3\cdot k^2\cdot x,$ $x\in \mathbb{R},$

eine Funktion $f_k$ gegeben.

(1)

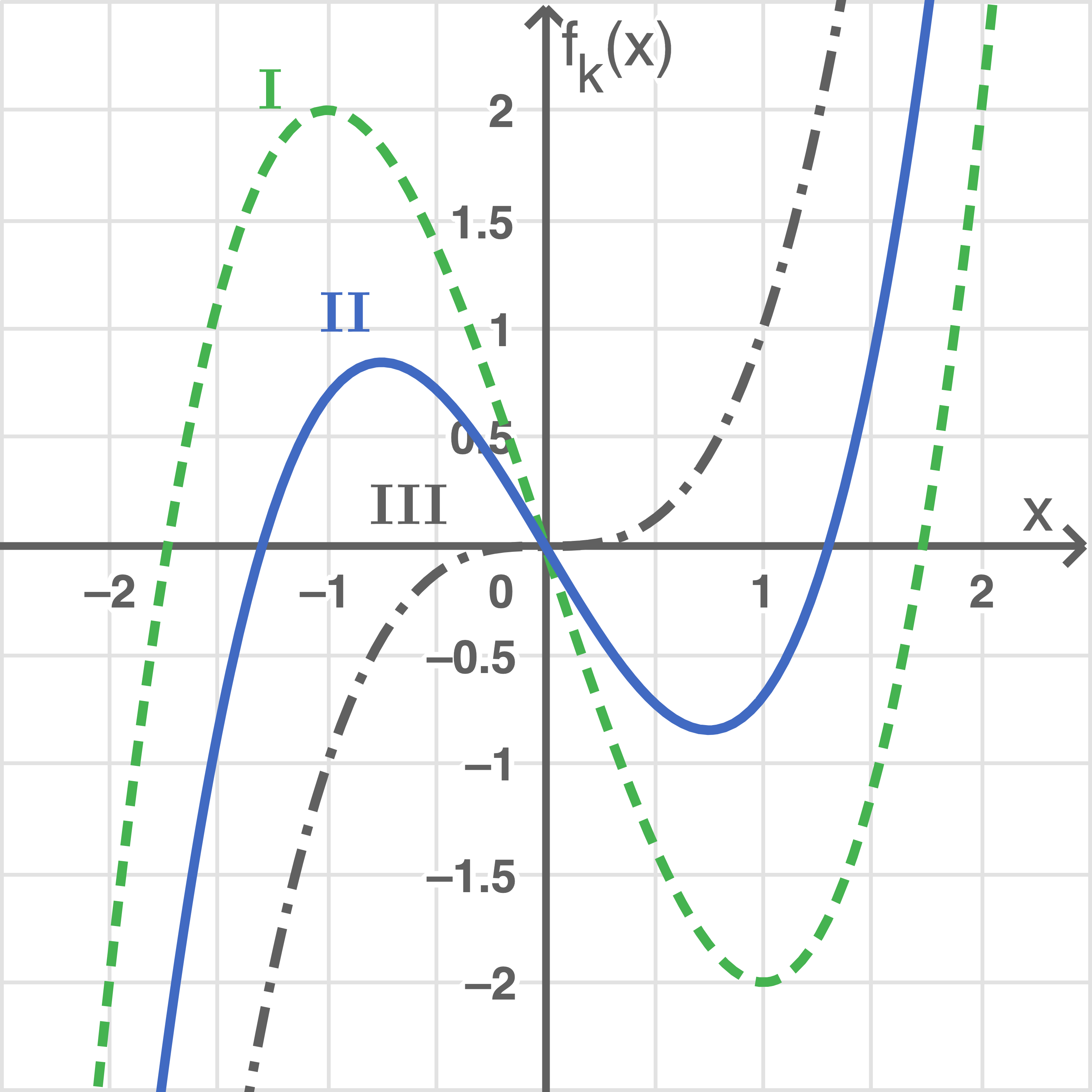
Die in der nebenstehenden Abbildung 1 dargestellten Graphen $\text{I},$ $\text{II}$ und $\text{III}$ gehören jeweils zu einem der Werte $k = 0 ,$ $k = 0,75$ und $k = 1.$

Entscheide, welcher Wert zu welchem Graphen gehört.

(2)

Ermittle rechnerisch in Abhängigkeit von $k \geq 0$ die lokalen Extrempunkte des Graphen von $f_k$ und die Art der Extrempunkte (falls vorhanden).

(3)

Ermittle die Wendestelle von $f_k$ und bestimme denjenigen Wert von $k,$ für den die Steigung der Tangente an den Graphen von $f_k$ im Wendepunkt $-3$ beträgt.

Abbildung 1

(3 + 8 + 6 Punkte)

(1)

Bestimme den Inhalt der Fläche, die für $x \leq 0$ vom Graphen von $f_1$ und der $x$ -Achse eingeschlossen wird.

Für jede reelle Zahl $a$ ist durch $g_a:\, y= a\cdot x$ ine Gerade $g_a$ durch den Ursprung des Koordinatensystems gegeben.

(2)

Ermittle in Abhängigkeit von $a$ die Anzahl der Schnittpunkte des Graphen von $f_1$ und der Geraden $g_a.$

(3)

Die Fläche, die für $x\leq 0$ vom Graphen von $f_1$ und der $x$ -Achse eingeschlossen wird, soll durch eine Gerade $g_a$ in zwei gleich große Teilflächen unterteilt werden.
Bestimme den passenden Wert von $a.$

(4 + 4 + 5 Punkte)

Für jede reelle Zahl $k \geq 0$ ist durch $t_k:\, y = \left(0,75-3\cdot k^2 \right) \cdot x +0,25$ eine Tangente an den Graphen von $f_k$ im Punkt $P_k(-0,5\mid f_k(-0,5))$ gegeben.

[Nachweis nicht erforderlich.]

(1)

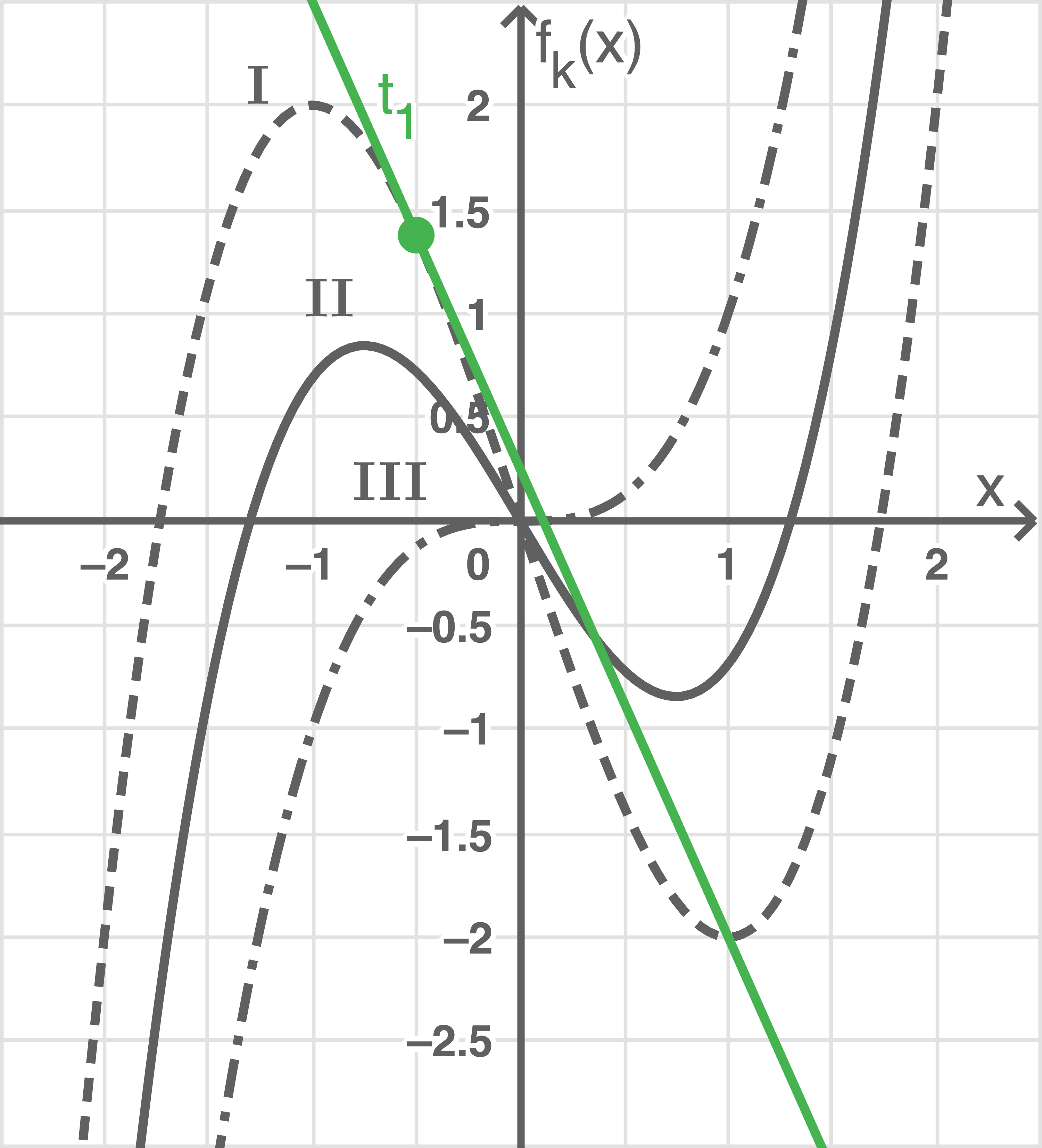
Zeichne die Tangente $t_1$ in die Abb. 1 ein.

(2)

Die Tangente $t_k$ und der Graph von $f_k$ schließen eine Fläche ein. Weise nach, dass die Größe dieser Fläche nicht vom Parameter $k$ abhängt, indem du den Inhalt dieser Fläche bestimmst.

(3)

Zeige: Für jede reelle Zahl $r \gt 0$ ist die Gerade durch die Punkte $A_{r;k}(-r\mid f_k(-r))$ und $B_{r;k}(2\cdot r \mid f_k(2\cdot r))$ eine Tangente an den Graphen von $f_k$ an der Stelle $x=-r.$

Abbildung 2

(2 + 4 + 4 Punkte)

(1)

Der Graph von $f(x)=x^3$ besitzt keine Extrempunkte. Zu $k=0$ gehört also der Graph $\text{III}.$ Je größer der Wert von $k,$ desto extremer werden auch die Extrema von $f_k.$

$k=0$ gehört zu Graph $\text{III}$

$k=0,75$ gehört zu Graph $\text{II}$

$k=1$ gehört zu Graph $\text{I}$

(2)

1. Schritt: Ableitungsfunktionen bestimmen

$\begin{array}[t]{rll} f_k(x) &=& x^3-3k^2\cdot x \\[5pt] f_k‘(x) &=& 3x^2 -3k^2 \\[5pt] f_k‘‘(x) &=& 6x \end{array}$

2. Schritt: Notwendiges Kriterium für lokale Extremstellen anwenden

$\begin{array}[t]{rll} x_1 &=& -k \\[5pt] x_2 &=& k \end{array}$

Vollständige Lösung anzeigen

3. Schritt: Hinreichendes Kriterium überprüfen

$\begin{array}[t]{rll} f_k‘‘(-k)&=& 6\cdot (-k) &\quad \scriptsize \mid\; k\geq 0 \\[5pt] &=& -6k \leq 0 \\[10pt] f_k‘‘(k)&=& 6\cdot k &\quad \scriptsize \mid\; k\geq 0 \\[5pt] &\geq& 0 \\[10pt] \end{array}$

Für $k \gt 0$ ist $\(f_k$ und $\(f_k$ also besitzt der Graph $f_k$ an der Stelle $x_1= -k$ einen lokalen Hochpunkt, an der Stelle $x_2=k$ einen lokalen Tiefpunkt.
Für $k=0$ ist $f_k(x)= x^3.$ Der Graph dieser Funktion besitzt keine lokalen Extrempunkte.

4. Schritt: $y$ -Koordinate berechnen

$\begin{array}[t]{rll} f_k(-k) &=& (-k)^3-3k^2\cdot (-k) \\[5pt] &=& 2k^3 \\[10pt] f_k(k) &=& k^3-3k^2\cdot k \\[5pt] &=& -2k^3 \\[5pt] \end{array}$

Für $k=0$ besitzt der Graph von $f_k$ keine lokalen Extrempunkte. Für $k\gt 0$ besitzt der Graph von $f_k$ den Hochpunkt $H(-k\mid 2k^3)$ und den Tiefpunkt $T(k\mid -2k^3).$

(3)

1. Schritt: Notwendiges Kriterium für Wendestellen anwenden

$\(\begin{array}[t]{rll} f_k$

2. Schritt: Hinreichendes Kriterium überprüfen

$\(f_k$

also ist insbesondere $f_k‘‘‘(0) = 6 \neq 0$

Die Wendestelle von $f_k$ ist also $x_W=0.$

Die Steigung der Tangente an den Graphen von $f_k$ im Wendepunkt beträgt:

$\begin{array}[t]{rll} m &=& f_k‘(0) \\[5pt] &=& 3\cdot 0^2 -3\cdot k^2 \\[5pt] &=& -3\cdot k^2 \\[5pt] \end{array}$

Gleichsetzen mit $-3$ liefert:

$\begin{array}[t]{rll} m &=& -3 \\[5pt] -3\cdot k^2 &=& -3 &\quad \scriptsize \mid\; :(-3)\\[5pt] k^2 &=& 1 \\[5pt] k_1 &=& 1 \\[5pt] k_2 &=& -1 \end{array}$

Da $k \geq 0$ vorgegeben ist, bleibt nur $k_1 =1.$ Für $k=1$ beträgt also die Steigung der Tangente an den Graphen von $f_k$ im Wendepunkt $-3.$

(1)

1. Schritt: Integrationsgrenzen bestimmen

Die Integrationsgrenzen entsprechen den Nullstellen von $f_1$ für $x \leq 0.$ Die Gleichung $f_1(x)=0$ wird mit dem solve-Befehl des CAS gelöst:

$\begin{array}[t]{rll} f_1(x) &=& 0 \\[5pt] x^3-3\cdot 1^2 \cdot x &=& 0 \\[5pt] x_1&=& 0 \\[5pt] x_2 &=& -\sqrt{3} \\[5pt] x_3 &=& \sqrt{3} \end{array}$

2. Schritt: Flächeninhalt bestimmen

$\blacktriangleright$ TI nspire CAS

menu $\to$ 4: Analysis $\to$ 3: Integral

$\blacktriangleright$ Casio Classpad II

keyboard $\to$ Math2 $\to$ $\int_{\Box}^{\Box}\Box$

$A=2,25$

Vollständige Lösung anzeigen

Der Inhalt der Fläche, die der Graph von $f_1$ für $x\leq 0$ mit der $x$ -Achse einschließt, beträgt $2,25\,\text{FE}.$

(2)

Mit dem solve-Befehl des CAS ergibt sich:

$\begin{array}[t]{rll} f_1 (x) &=& g_a(x) &\quad \scriptsize \mid\; CAS \\[5pt] x_1 &=& -\sqrt{a+3} \\[5pt] x_2 &=& 0 \\[5pt] x_3 &=& \sqrt{a+3} \end{array}$

Vollständige Lösung anzeigen

$x_1$ und $x_3$ existieren nur für $a\geq -3,$ da der Radikand unter der Wurzel sonst negativ wäre. Für $a=-3$ gilt $x_1 = x_2 =x_3.$ Also gilt insgesamt:

Für $a\gt -3$ besitzen die Graphen von $f_1$ und $g_a$ drei Schnittpunkte.
Für $a \leq -3$ besitzen die Graphen von $f_1$ und $g_a$ genau einen Schnittpunkt.

(3)

Damit die Gerade $g_a$ die Fläche halbiert, muss der Inhalt der Fläche, die der Graph von $f_1$ und die Gerade $g_a$ einschließen die Hälfte von $A$ betragen.

1. Schritt: Flächeninhalt der Fläche zwischen den beiden Graphen bestimmen

Den Inhalt der Fläche zwischen den beiden Graphen $f_1$ und $g_a$ wird mit Hilfe eines Integrals berechnet:

$I_a = ...$

Vollständige Lösung anzeigen

2. Schritt: Gleichsetzen

Es ist also $a$ gesucht, sodass für den Flächeninhalt $I_a$ gilt:

$... = 1,125$

Vollständige Lösung anzeigen

Diese Gleichung wird mit dem solve-Befehl des CAS gelöst:

$\begin{array}[t]{rll} a_1 &=& \dfrac{-3\cdot \sqrt{2}}{2}-3 \approx -5,12 \\[5pt] a_2 &=& \dfrac{3\cdot \sqrt{2}}{2}-3 \approx -0,88 \end{array}$

Da $a_1 \lt -3$ ist und sich die Graphen von $f_1$ und $g_a$ für diese Werte nur in einem gemeinsamen Punkt schneiden, kommt nur $a_2$ als Lösung in Frage.
Für $a= \dfrac{3\cdot \sqrt{2}}{2}-3\approx -0,88$ unterteilt die Gerade $g_a$ das vom Graphen von $f_1$ und der $x$ -Achse eingeschlossene Flächenstück in zwei gleich große Teilstücke.

(1)

(2)

1. Schritt: Integrationsgrenzen bestimmen

$\begin{array}[t]{rll} t_k(x) &=& f_k(x) \\[5pt] x_1 &=& -0,5 \\[5pt] x_2 &=& 1 \end{array}$

2. Schritt: Flächeninhalt bestimmen

$A_k = \frac{27}{64}$

Vollständige Lösung anzeigen

Der Inhalt der von den Graphen von $t_k$ und $f_k$ eingeschlossenen Fläche beträgt $\frac{27}{64}\,\text{FE}$ und hängt daher nicht von $k$ ab.

(3)

1. Schritt: Steigung der Gerade durch $A_{r;k}$ und $B_{r;k}$ bestimmen

$\begin{array}[t]{rll} m_{A;B} &=& \dfrac{f_k(2\cdot r)- f_k(-r)}{2\cdot r -(-r)} \\[5pt] &=& \dfrac{(2r)^3-3\cdot k^2\cdot 2\cdot r - \left( (-r)^3 -3\cdot k^2\cdot (-r)\right)}{3r} \\[5pt] &=& \dfrac{8r^3-6\cdot k^2\cdot r - \left( -r^3 +3\cdot k^2\cdot r\right)}{3r} \\[5pt] &=& \dfrac{8r^3-6\cdot k^2\cdot r +r^3 -3\cdot k^2\cdot r}{3r} \\[5pt] &=& \dfrac{9r^3-9\cdot k^2\cdot r}{3r} \\[5pt] &=& 3r^2-3\cdot k^2 \\[5pt] \end{array}$

2. Schritt: Steigung der Tangente an der Stelle $x=-r$ bestimmen

$\begin{array}[t]{rll} f_k‘(-r)&=& 3\cdot (-r)^2 -3\cdot k^2 \\[5pt] &=& 3r^2-3k^2 \end{array}$

Die Steigung der Geraden durch die Punkte $A_{r;k}$ und $B_{r;k}$ stimmt mit der Steigung der Tangente an den Graphen von $f_k$ an der Stelle $x=-r$ überein. Zudem verlaufen beide Geraden durch den Punkt $(-r\mid f_k(-r))$ und sind damit identisch. Die Gerade durch die Punkte $A_{r;k}$ und $B_{r;k}$ ist also eine Tangente an den Graphen von $f_k$ an der Stelle $x=-r.$