Analysis 2
a)
Gegeben ist die Schar der in  definierten Funktionen
definierten Funktionen  mit
mit  und
und 
(1)
Berechne die Stellen, an denen der Graph von  eine Steigung von
eine Steigung von  hat.
hat.
(2)
Bestimme den Wert von  so, dass der Punkt
so, dass der Punkt  auf dem Graphen von
auf dem Graphen von  liegt.
liegt.
(3)
Ermittle die Koordinaten der gemeinsamen Punkte der Graphen von  und
und  Weise nach, dass es nur einen Punkt gibt, der auf jedem Graphen der Schar liegt.
Weise nach, dass es nur einen Punkt gibt, der auf jedem Graphen der Schar liegt.
(4)
Die Gleichung  hat in Abhängigkeit von
hat in Abhängigkeit von  die Lösungen
die Lösungen  und
und  und
und  wobei die Lösung
wobei die Lösung  nicht mit den anderen beiden Lösungen zusammenfallen kann.
Gib die Anzahl der Nullstellen von
nicht mit den anderen beiden Lösungen zusammenfallen kann.
Gib die Anzahl der Nullstellen von  in Abhängigkeit von
in Abhängigkeit von  an und begründe deine Angabe anhand der obigen Terme.
an und begründe deine Angabe anhand der obigen Terme.
(5)
Der Graph jeder Funktion  hat genau einen Wendepunkt.
Bestimme den Wert von
hat genau einen Wendepunkt.
Bestimme den Wert von  zu dem Wendepunkt mit der größten
zu dem Wendepunkt mit der größten  -Koordinate.
-Koordinate.
(6)
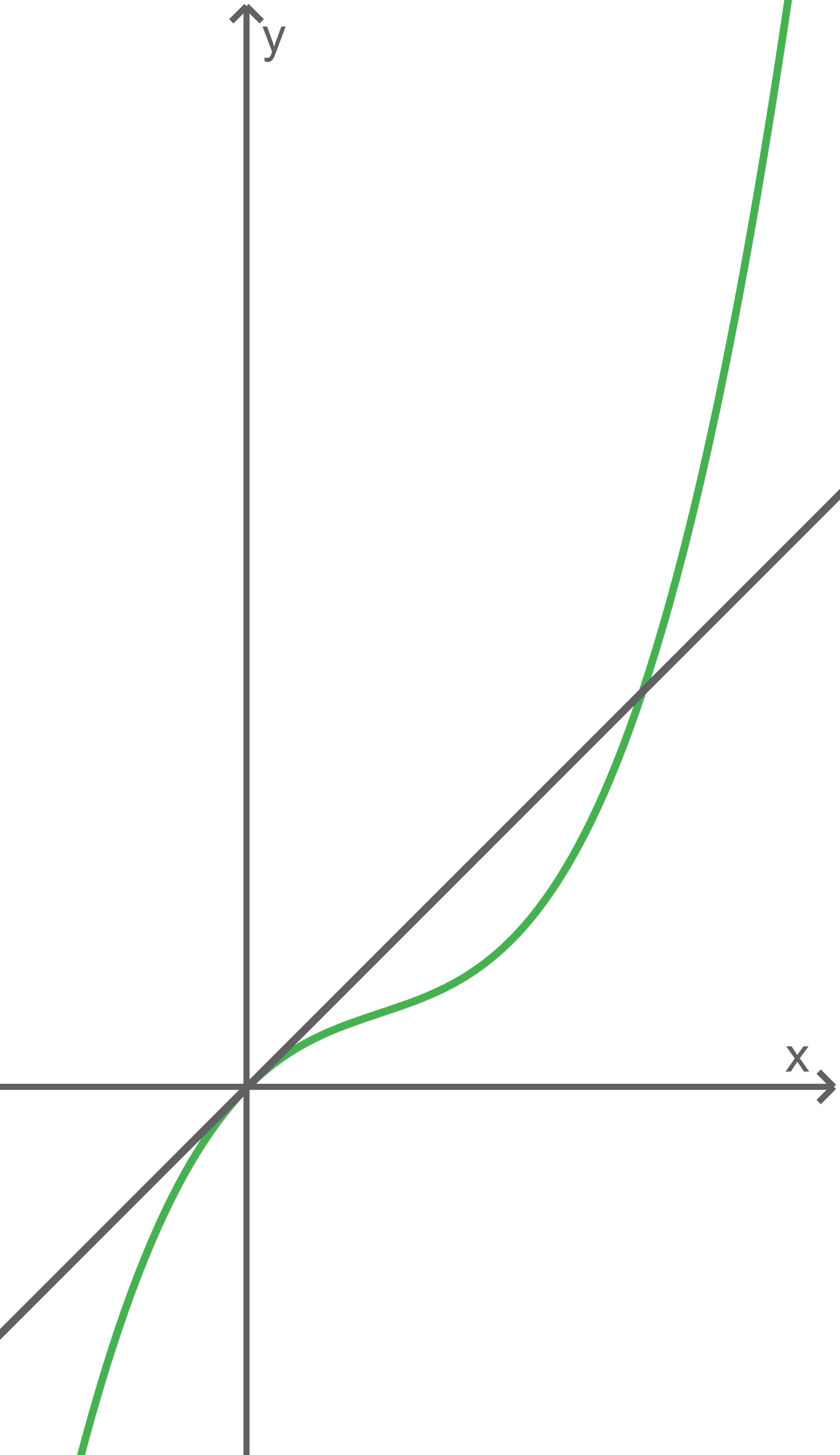
Im Folgenden gilt  Abbildung 1 zeigt beispielhaft den Graphen einer Funktion
Abbildung 1 zeigt beispielhaft den Graphen einer Funktion  sowie die Gerade
sowie die Gerade  mit der Gleichung
mit der Gleichung  die den Graphen in den Punkten
die den Graphen in den Punkten  und
und  schneidet. Die Gerade
schneidet. Die Gerade  die
die  -Achse und die Gerade mit der Gleichung
-Achse und die Gerade mit der Gleichung  begrenzen ein rechtwinkliges Dreieck.
begrenzen ein rechtwinkliges Dreieck.
 Die folgenden Schritte stellen die Lösung einer Aufgabe dar:
Die folgenden Schritte stellen die Lösung einer Aufgabe dar:
 geometrisch.
geometrisch.

Abb. 1
(7)
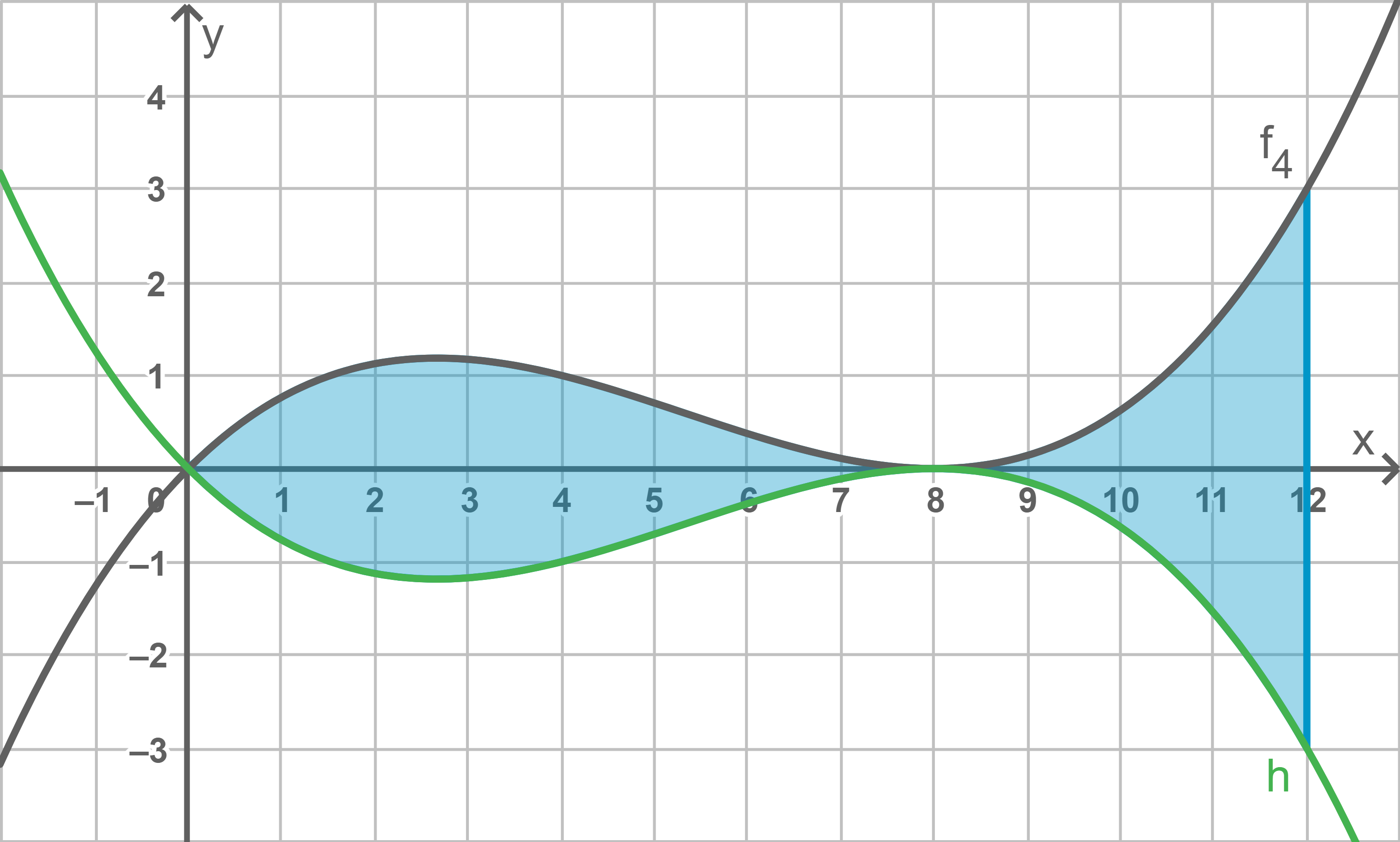
Abbildung 2 zeigt den Graphen der Funktion 
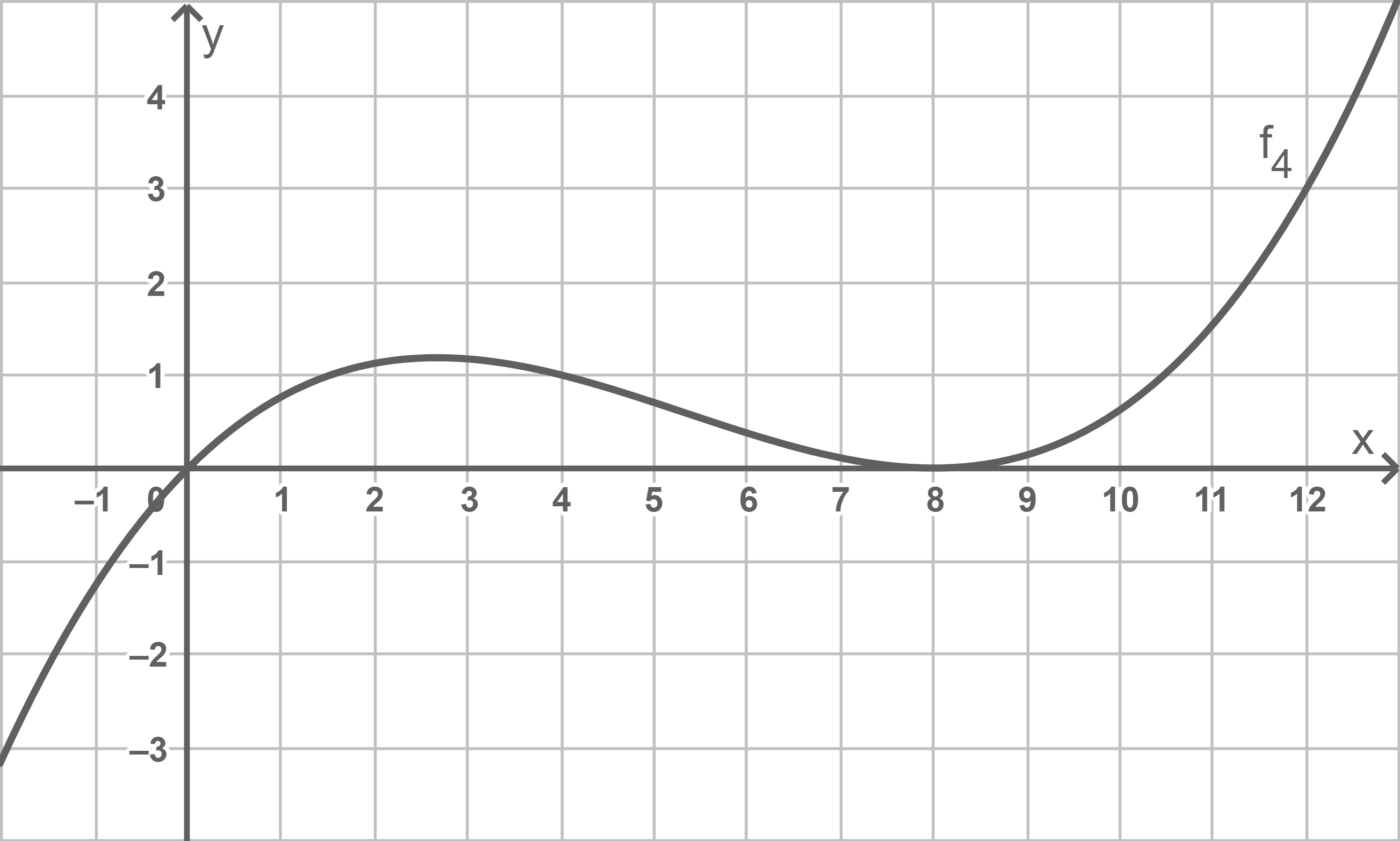
 ist die Funktion, deren Graph durch Spiegelung des Graphen von
ist die Funktion, deren Graph durch Spiegelung des Graphen von  an der
an der  -Achse entsteht.
-Achse entsteht.

Abb. 2
(i)
Skizziere in Abbildung 2 den Graphen von  sowie die Fläche
sowie die Fläche  die von
die von  bis
bis  zwischen den Graphen von
zwischen den Graphen von  und
und  liegt.
liegt.
(ii)
Berechne den Inhalt der Fläche 
(iii)
Es gibt einen Wert von  für den die Fläche, die im Bereich von
für den die Fläche, die im Bereich von  bis
bis  zwischen dem Graphen von
zwischen dem Graphen von  und der
und der  -Achse liegt, den Flächeninhalt
-Achse liegt, den Flächeninhalt  besitzt.
Gib eine Gleichung an, mit der man diesen Wert von
besitzt.
Gib eine Gleichung an, mit der man diesen Wert von  ermitteln kann.
ermitteln kann.
(3 + 2 + 5 + 4 + 5 + 5 + 6 Punkte)
b)
Für ein Umweltschutzprojekt soll eine Unterwasserdrohne  in einem See Messungen in unterschiedlichen Tiefen vornehmen. Sie bewegt sich nur in vertikaler Richtung, d. h. senkrecht zur Wasseroberfläche des Sees. Ihre Geschwindigkeit lässt sich für
in einem See Messungen in unterschiedlichen Tiefen vornehmen. Sie bewegt sich nur in vertikaler Richtung, d. h. senkrecht zur Wasseroberfläche des Sees. Ihre Geschwindigkeit lässt sich für  mithilfe der in
mithilfe der in  definierten Funktion
definierten Funktion  beschreiben, wobei gilt:
beschreiben, wobei gilt:
 Dabei ist
Dabei ist  die seit Beobachtungsbeginn vergangene Zeit in Minuten,
die seit Beobachtungsbeginn vergangene Zeit in Minuten,  die Geschwindigkeit von
die Geschwindigkeit von  in Meter pro Minute. Wenn die Geschwindigkeit in diesem Modell negativ ist, sinkt die Unterwasserdrohne. Wenn die Geschwindigkeit positiv ist, steigt die Unterwasserdrohne.
in Meter pro Minute. Wenn die Geschwindigkeit in diesem Modell negativ ist, sinkt die Unterwasserdrohne. Wenn die Geschwindigkeit positiv ist, steigt die Unterwasserdrohne.
(1)
Bestimme die Koordinaten des Tiefpunktes des Graphen von  und interpretiere die Werte im Sachkontext.
und interpretiere die Werte im Sachkontext.
(2)
Mit  wird die erste Ableitungsfunktion von
wird die erste Ableitungsfunktion von  bezeichnet. Innerhalb eines bestimmten Zeitraums gilt für jeden Zeitpunkt
bezeichnet. Innerhalb eines bestimmten Zeitraums gilt für jeden Zeitpunkt  die folgende Aussage:
die folgende Aussage:  und
und  Interpretiere dies in Bezug auf die Bewegung von
Interpretiere dies in Bezug auf die Bewegung von  in diesem Zeitraum.
in diesem Zeitraum.
(3)
Im Beobachtungszeitraum beträgt der geringste Abstand von  zur Wasseroberfläche des Sees
zur Wasseroberfläche des Sees  Meter.
Ermittle den Abstand von
Meter.
Ermittle den Abstand von  zur Wasseroberfläche zu Beobachtungsbeginn.
zur Wasseroberfläche zu Beobachtungsbeginn.
(3 + 2 + 5 Punkte)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
(1)
Mit dem CAS folgt für die erste Ableitung von 
 Für die gesuchten Stellen folgt somit:
Für die gesuchten Stellen folgt somit:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/d86de72ac720d429281492175a5c636687086fd38b0a1d82b38627b06066f47c?color=5a5a5a) Mit dem solve-Befehl des CAS ergibt sich
Mit dem solve-Befehl des CAS ergibt sich  und
und 
(2)
(3)
Koordinaten der gemeinsamen Punkte ermitteln
Gleichsetzen von  und
und  liefert:
Mit dem solve-Befehl des CAS folgt:
liefert:
Mit dem solve-Befehl des CAS folgt:
![\(\begin{array}[t]{rll}
x_1&=&0 \\[5pt]
x_2&=&\dfrac{4}{7}
\end{array}\)](https://mathjax.schullv.de/5886005d9479c0bac710ea72ee3532e13c9453ea74b46d2796ff9a0357f87885?color=5a5a5a) Einsetzen in z.B.
Einsetzen in z.B.  liefert:
liefert:
![\(\begin{array}[t]{rll}
f_1(0)&=&0^3-0^2+0 \\[5pt]
&=&0
\end{array}\)](https://mathjax.schullv.de/e890317448b6d2b2981d090a2d662401768e49da414cf9e266acdce270d85ce8?color=5a5a5a)
![\(\begin{array}[t]{rll}
f_1\left(\dfrac{4}{7}\right)&=&\left(\dfrac{4}{7}\right)^3-\left(\dfrac{4}{7}\right)^2+\dfrac{4}{7} \\[5pt]
&=&\dfrac{64}{343}-\dfrac{16}{49}+\dfrac{4}{7} \\[5pt]
&=&\dfrac{148}{343}
\end{array}\)](https://mathjax.schullv.de/3e760425e4cd29ef6f997d92cc3cc07598d5fbd7545a9e002d2fee3f650392cf?color=5a5a5a) Die Koordinaten der gemeinsamen Punkte der Graphen von
Die Koordinaten der gemeinsamen Punkte der Graphen von  und
und  sind somit gegeben durch
sind somit gegeben durch  und
und  Nachweisen, dass es genau einen gemeinsamen Punkt der Schar gibt
Nach den Werten von eben kommen nur die Stellen
Nachweisen, dass es genau einen gemeinsamen Punkt der Schar gibt
Nach den Werten von eben kommen nur die Stellen  und
und  infrage. Da
infrage. Da 
 gilt, folgt mit dem Satz des Nullprodukts unabhängig von
gilt, folgt mit dem Satz des Nullprodukts unabhängig von  dass
dass  gilt. Einsetzen von
gilt. Einsetzen von  in z.B.
in z.B.  liefert:
liefert:
![\(\begin{array}[t]{rll}
f_3\left(\dfrac{4}{7}\right)&=&\dfrac{1}{3^3}\cdot\left(\dfrac{4}{7}\right)^3-\dfrac{1}{3}\cdot\left(\dfrac{4}{7}\right)^2+\dfrac{4}{7} \\[5pt]
&=&\dfrac{64}{343\cdot27}-\dfrac{16}{49\cdot3}+\dfrac{4}{7} \\[5pt]
&=&\dfrac{4348}{9261}\neq\dfrac{151}{343}
\end{array}\)](https://mathjax.schullv.de/f99d86c3424fd0e2f333b42765b4971522816c5ebeb17e8c9230ab024ee375da?color=5a5a5a) Somit existiert nur ein Punkt, welcher auf jedem Graphen der Schar liegt.
Somit existiert nur ein Punkt, welcher auf jedem Graphen der Schar liegt.
(4)
Wenn  gilt, ist der Term unter der Wurzel im Zähler der letzten beiden Nullstellen positiv und es gibt somit zwei weitere Nullstellen außer
gilt, ist der Term unter der Wurzel im Zähler der letzten beiden Nullstellen positiv und es gibt somit zwei weitere Nullstellen außer  Damit hat
Damit hat  drei Nullstellen.
Für
drei Nullstellen.
Für  ist der Term unter der Wurzel null und die beiden letzten Nullstellen fallen zusammen zu einer, das heißt
ist der Term unter der Wurzel null und die beiden letzten Nullstellen fallen zusammen zu einer, das heißt  besitzt zwei Nullstellen.
Für
besitzt zwei Nullstellen.
Für  ist der Term unter der Wurzel negativ und
ist der Term unter der Wurzel negativ und  besitzt somit nur eine Nullstelle.
besitzt somit nur eine Nullstelle.
(5)
Mit dem CAS ergibt sich:

 Die notwendige Bedingung
Die notwendige Bedingung  für Wendestellen liefert mit dem solve-Befehl des CAS:
für Wendestellen liefert mit dem solve-Befehl des CAS:
 Da der Graph jeder Funktion
Da der Graph jeder Funktion  laut Aufgabenstellung genau einen Wendepunkt besitzt, kann auf die Überprüfung der hinreichenden Bedingung verzichtet werden.
Für die
laut Aufgabenstellung genau einen Wendepunkt besitzt, kann auf die Überprüfung der hinreichenden Bedingung verzichtet werden.
Für die  -Koordinaten der Wendepunkte folgt:
Die Wendepunkte liegen also auf dem Graphen der Funktion
-Koordinaten der Wendepunkte folgt:
Die Wendepunkte liegen also auf dem Graphen der Funktion  Für die ersten beiden Ableitungen von
Für die ersten beiden Ableitungen von  folgt mit dem CAS:
folgt mit dem CAS:

 1. Schritt: Notwendige Bedingung für Extremstellen anwenden
1. Schritt: Notwendige Bedingung für Extremstellen anwenden
 Mit dem solve-Befehl des CAS ergibt sich:
Mit dem solve-Befehl des CAS ergibt sich:
![\(\begin{array}[t]{rll}
a_1&=&0 \\[5pt]
a_2&=&3
\end{array}\)](https://mathjax.schullv.de/4a57a0c96d4cd28156e9e78bf1a7b27b5e50368bfb7a1bea07a6d054d7fb570c?color=5a5a5a) 2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
![\(\begin{array}[t]{rll}
g](https://mathjax.schullv.de/2e55e1a7b04a85da2f65698b99f51b3f500ba137971c3eb7087301235e32b031?color=5a5a5a)
![\(\begin{array}[t]{rll}
g](https://mathjax.schullv.de/718b478b4ac7f6a828c6fdb6f68084ae22e8687e50d6b65e58456dcffbb2b230?color=5a5a5a) Somit besitzt
Somit besitzt  an der Stelle
an der Stelle  einen Hochpunkt, das heißt für
einen Hochpunkt, das heißt für  wird die
wird die  -Koordinate des Wendepunkts der Schar
-Koordinate des Wendepunkts der Schar  maximal.
maximal.
(6)
Schritte erläutern
Im ersten Schritt wird die Gleichung  gelöst, was die Schnittpunkte der Funktion
gelöst, was die Schnittpunkte der Funktion  mit der Geraden
mit der Geraden  liefert.
liefert.
Im zweiten Schritt wird der Inhalt der Fläche des rechtwinkligen Dreiecks mit dem dreifachen Inhalt der Fläche, die die beiden Graphen von und
und  miteinander einschließen, gleichgesetzt. Diese Gleichheit ist für den Wert
miteinander einschließen, gleichgesetzt. Diese Gleichheit ist für den Wert  erfüllt.
Lösung geometrisch interpretieren
Für
erfüllt.
Lösung geometrisch interpretieren
Für  beträgt das Verhältnis des rechtwinkligen Dreiecks zur eingeschlossenen Fläche zwischen den beiden Graphen
beträgt das Verhältnis des rechtwinkligen Dreiecks zur eingeschlossenen Fläche zwischen den beiden Graphen 
Im zweiten Schritt wird der Inhalt der Fläche des rechtwinkligen Dreiecks mit dem dreifachen Inhalt der Fläche, die die beiden Graphen von
(7)
b)
(1)
Koordinaten des Tiefpunktes bestimmen
Für die ersten beiden Ableitungen von  folgt mit dem CAS:
folgt mit dem CAS:

 1. Schritt: Notwendige Bedingung für Extremstellen anwenden
1. Schritt: Notwendige Bedingung für Extremstellen anwenden
 Da die
Da die  -Funktion stets ungleich null ist, ergeben sich die Nullstellen von
-Funktion stets ungleich null ist, ergeben sich die Nullstellen von  als die der Gleichung
als die der Gleichung  Mit dem CAS ergibt sich:
Mit dem CAS ergibt sich:
![\(\begin{array}[t]{rll}
t_1&\approx&2,23 \\[5pt]
t_2&\approx&14,02
\end{array}\)](https://mathjax.schullv.de/c4dfc2a5cd67043a0edcd13079f451d8be9238621000324077a3057485104ff2?color=5a5a5a) 2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen

 Der Graph von
Der Graph von  besitzt somit bei
besitzt somit bei  einen Tiefpunkt. Für dessen
einen Tiefpunkt. Für dessen  -Koordinate folgt:
-Koordinate folgt:
 Für die Koordinaten des gesuchten Tiefpunktes folgt somit ca.
Für die Koordinaten des gesuchten Tiefpunktes folgt somit ca.  Werte im Sachkontext interpretieren
Nach ca.
Werte im Sachkontext interpretieren
Nach ca.  Minuten sinkt die Unterwasserdrohne mit einer Geschwindigkeit von
Minuten sinkt die Unterwasserdrohne mit einer Geschwindigkeit von  am schnellsten.
am schnellsten.
(2)
Die Bedingung  bedeutet, dass die Drohne sinkt, während
bedeutet, dass die Drohne sinkt, während  bedeutet, dass die Drohne nach oben beschleunigt wird. Insgesamt bewegt sich Drohne in diesem Zeitraum also immer weiter nach unten, allerdings mit immer niedrigerer Geschwindigkeit.
bedeutet, dass die Drohne nach oben beschleunigt wird. Insgesamt bewegt sich Drohne in diesem Zeitraum also immer weiter nach unten, allerdings mit immer niedrigerer Geschwindigkeit.
(3)
Der Zeitpunkt, zu dem die Unterwasserdrohne den geringsten Abstand zur Wasseroberfläche besitzt, ist die Stelle an der die Stammfunktionen von  einen Hochpunkt haben, das heißt
einen Hochpunkt haben, das heißt  muss dort eine Nullstelle besitzen. Da die
muss dort eine Nullstelle besitzen. Da die  -Funktion stets ungleich null ist, liefert
-Funktion stets ungleich null ist, liefert  nach dem Satz des Nullprodukts die Gleichung
nach dem Satz des Nullprodukts die Gleichung  Mit dem CAS ergibt sich:
Mit dem CAS ergibt sich:
![\(\begin{array}[t]{rll}
t_1&=&0 \\[5pt]
t_2&=&6,25
\end{array}\)](https://mathjax.schullv.de/bf272b930fcb4e81d3f9ea0a9f7971b554886bd3da7605ee019d5e16826642e8?color=5a5a5a) Es gilt
Es gilt  für
für  und
und  für
für 
 hat somit 6,25 Minuten nach Beobachtungsbeginn den kleinsten Abstand zur Wasseroberfläche.
Der Abstand von
hat somit 6,25 Minuten nach Beobachtungsbeginn den kleinsten Abstand zur Wasseroberfläche.
Der Abstand von  zur Wasseroberfläche zu Beobachtungsbeginn in Metern lässt sich wie folgt berechnen:
zur Wasseroberfläche zu Beobachtungsbeginn in Metern lässt sich wie folgt berechnen:
 Zu Beobachtungsbeginn hat
Zu Beobachtungsbeginn hat  einen Abstand von
einen Abstand von  zur Wasseroberfläche.
zur Wasseroberfläche.