Teil A: Ohne Hilfsmittel

Gegeben sind die Geraden

$g: \overrightarrow{x}=\pmatrix{3\\-3\\3} +r\cdot \pmatrix{3\\0\\-1}$ mit $r\in \mathbb{R}$ und $h:\overrightarrow{x}= \pmatrix{3\\-3\\3} + s\cdot \pmatrix{1\\0\\3}$ mit $s\in \mathbb{R}.$

(1)

Gib die Koordinaten des Schnittpunkts von $g$ und $h$ an und zeige, dass $g$ und $h$ senkrecht zueinander verlaufen.

(2)

Die Ebene $E$ enthält die Geraden $g$ und $h.$
Bestimme eine Gleichung von $E$ in Koordinatenform.

(2 + 4 Punkte)

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=\mathrm e^x+\frac{1}{2}x.$

(1)

Begründe, dass der Graph von $f$ und der Graph der in $\mathbb{R}$ definierten Funktion $g$ mit $g(x)=\dfrac{1}{2}x-1$ keinen gemeinsamen Punkt besitzen.

(2)

Für eine positive reelle Zahl $c$ wird die in $\mathbb{R}$ definierte Funktion $g_c$ mit $g_c(x)=\dfrac{1}{2}x-c$ betrachtet.
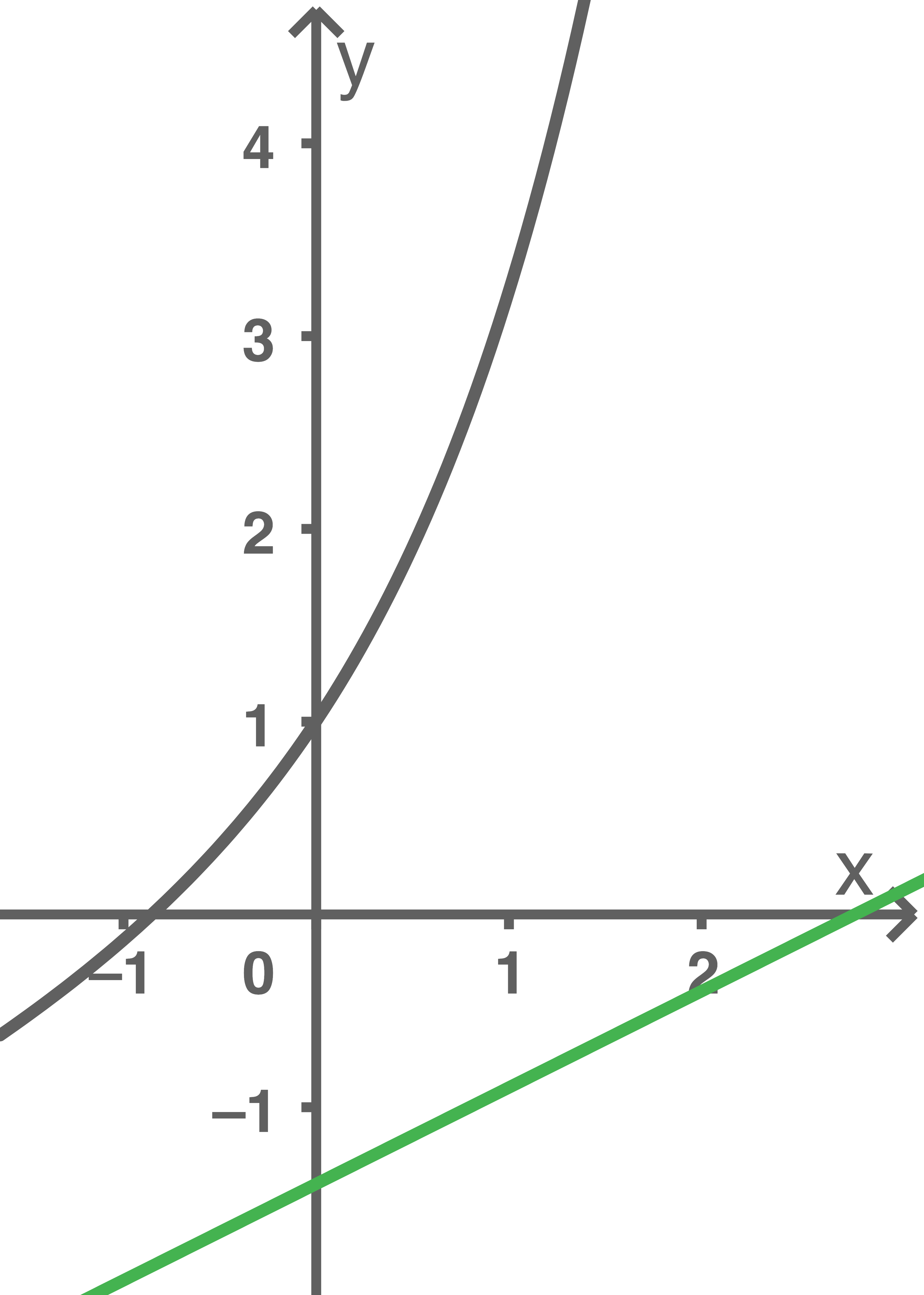
Die Abbildung 1 zeigt die Graphen von $f$ und $g_c.$
Die beiden Graphen schließen mit der $y$ -Achse und der Geraden mit der Gleichung $x = 1$ eine Fläche mit dem Inhalt $3$ ein.
Berechne $c.$

Abbildung 1

(2 + 4 Punkte)

Gegeben ist die quadratische Funktion $f$ mit $f(x)=x^2-3.$ Der Graph der Funktion $f$ ist in der Abbildung 2 dargestellt.

(1)

Bestimme alle Werte von $k\in \mathbb{R},$ für die $\displaystyle\int_{0}^{k}f(x)\;\mathrm dx = 0$ gilt.

(2)

Gib jeweils an, für welche $k\geq 0$ die Beziehungen

$\displaystyle\int_{0}^{k}f(x)\;\mathrm dx \lt 0$ bzw. $\displaystyle\int_{0}^{k}f(x)\;\mathrm dx \gt 0$

gelten.

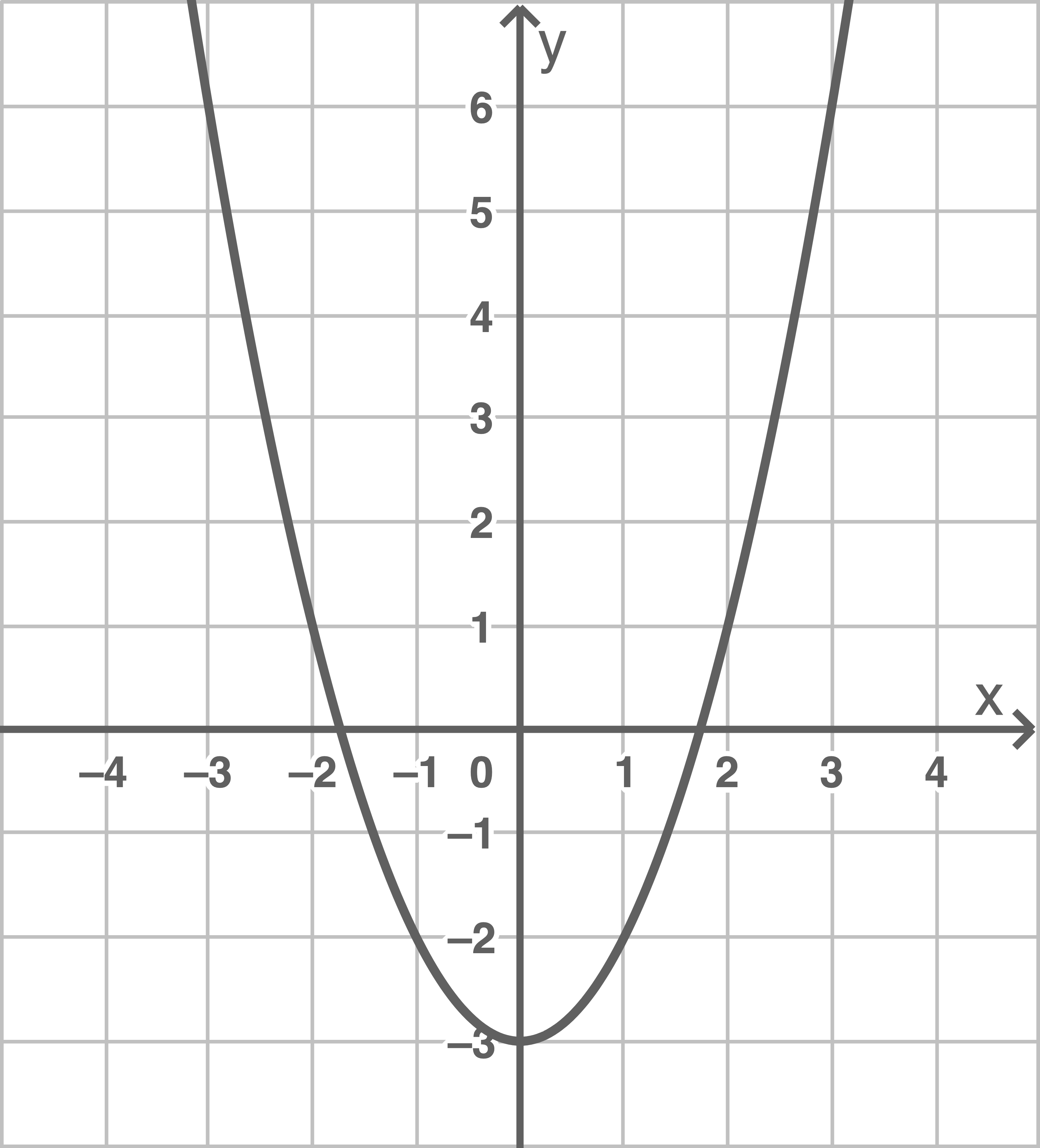
Abbildung 2

(4 + 2 Punkte)

(1)

Die Zufallsgröße $X$ ist binomialverteilt mit $n=10$ und $p=0,8.$ Eine der folgenden Abbildungen 3 bis 5 stellt die Wahrscheinlichkeitsverteilung von $X$ dar.

Abbildung 3

Abbildung 4

Abbildung 5

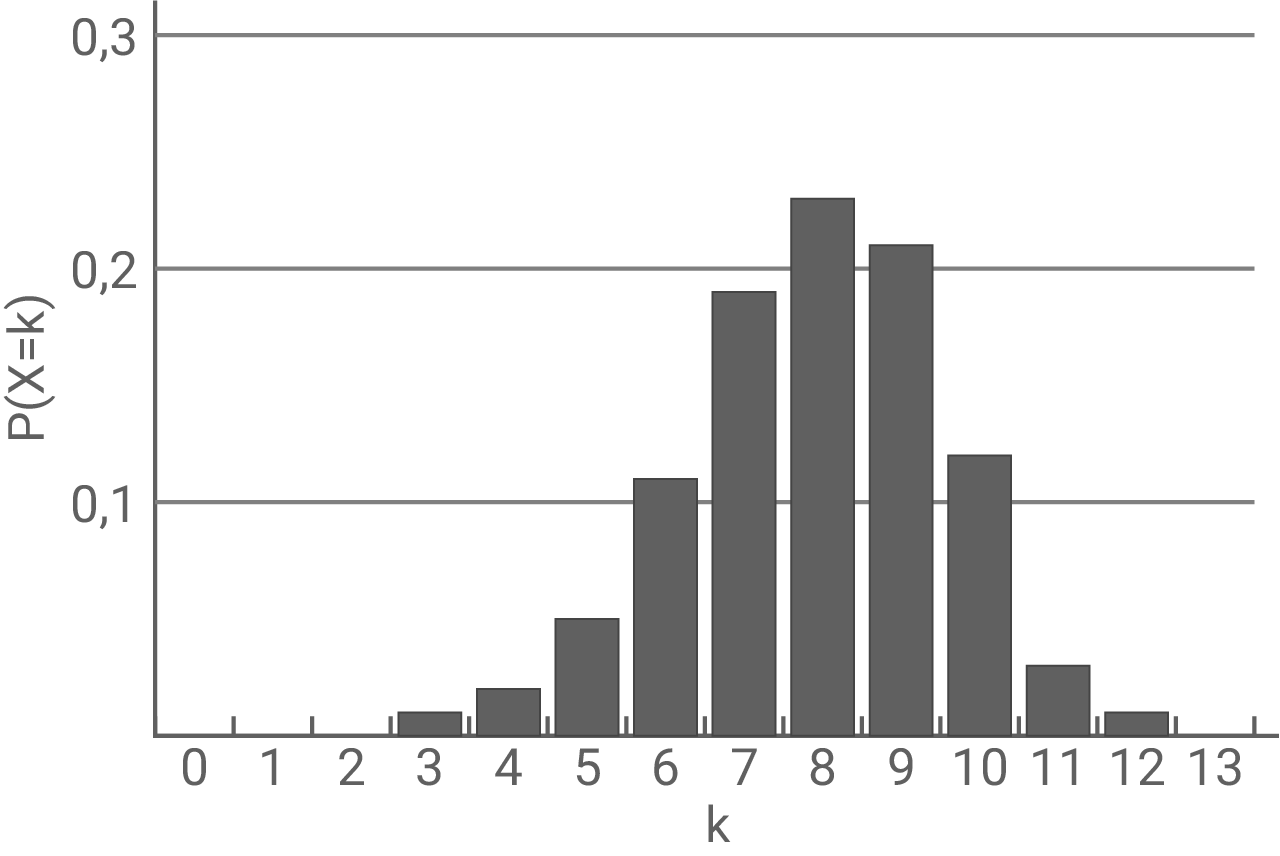
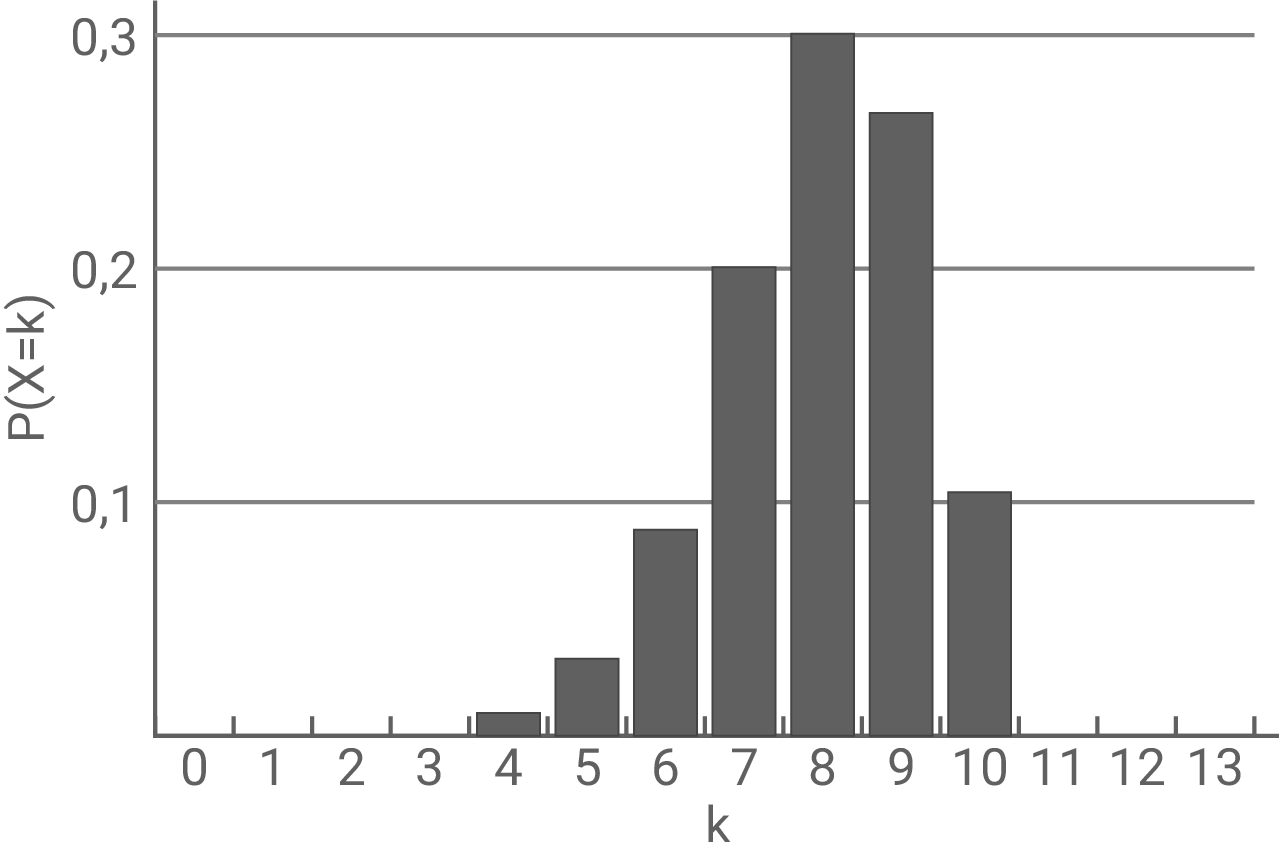
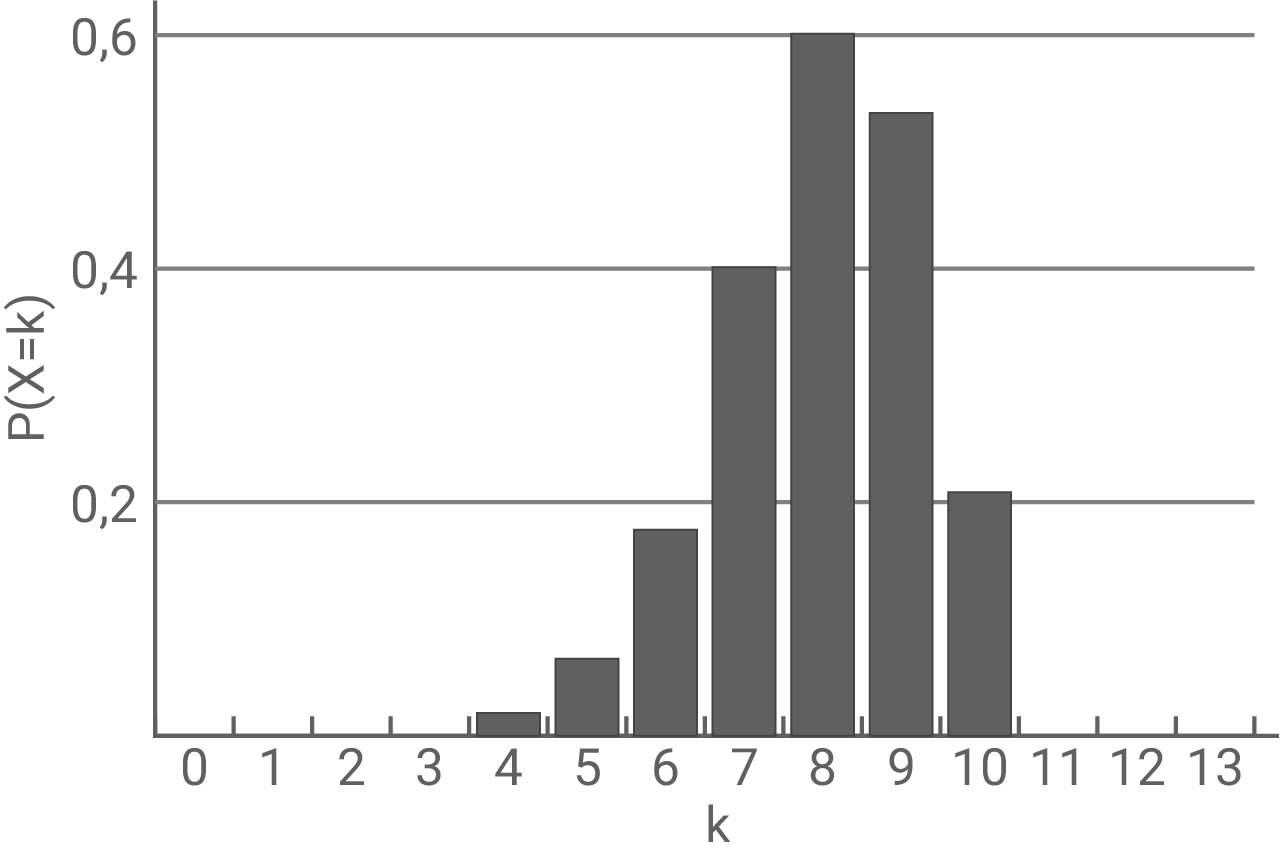Gib die beiden Abbildungen an, die die Wahrscheinlichkeitsverteilung von $X$ nicht darstellen. Begründe deine Angabe.

(2)

Betrachtet wird die binomialverteilte Zufallsgröße $Y$ mit den Parametern $n$ und $p.$

Es gilt:

Der Erwartungswert von $Y$ ist $8.$
Die Wahrscheinlichkeitsverteilung von $Y$ ist symmetrisch.

Ermittle den Wert von $n.$

(4 + 2 Punkte)

(1)

Die beiden Stützvektoren von $g$ und $h$ stimmen überein. Die beiden Geraden $g$ und $h$ haben also den gemeinsamen Punkt $P(3 \mid -3\mid 3).$

Die Geraden verlaufen senkrecht zueinander, wenn das Skalarprodukt der Richtungsvektoren Null ergibt.

$\begin{array}[t]{rll} \pmatrix{3\\0\\-1}\circ \pmatrix{1\\0\\3}&=&3\cdot 1 +0\cdot 0 -1\cdot 3 \\[5pt] &=& 0 \end{array}$

Die beiden Geraden verlaufen also senkrecht zueinander.

(2)

Ein Normalenvektor von $E$ kann über das Kreuzprodukt der beiden Richtungsvektoren der Geraden bestimmt werden:

$\overrightarrow{n} = \pmatrix{0\\-10\\0}$

Vollständige Lösung anzeigen

Punktprobe mit $(3\mid -3\mid 3):$

$d=30$

Vollständige Lösung anzeigen

Eine Gleichung in Koordinatenform von $E$ lautet:

$E:\quad -10x_2 = 30$

(1)

$... \mathrm e^x = -1$

Vollständige Lösung anzeigen

Da $\mathrm e^x$ nicht negativ werden kann, besitzt die Gleichung $f(x)=g(x)$ also keine Lösung. Die beiden Graphen von $f$ und $g$ können daher keine gemeinsamen Punkte besitzen.

(2)

Rechenweg anzeigen

$c= 4 -\mathrm e$

(1)

$\begin{array}[t]{rll} \displaystyle\int_{0}^{k}f(x)\;\mathrm dx &=& 0 \\[5pt] \displaystyle\int_{0}^{k}\left(x^2-3 \right)\;\mathrm dx &=& 0 \\[5pt] \left[\frac{1}{3}x^3 -3x \right]_0^k &=& 0 \\[5pt] \frac{1}{3}\cdot k^3 -3\cdot k - \left(\frac{1}{3}\cdot 0^3 -3\cdot 0\right) &=& 0 \\[5pt] \frac{1}{3}\cdot k^3 -3\cdot k &=& 0 \\[5pt] k\cdot \left(\frac{1}{3}\cdot k^2 -3 \right) &=& 0 \\[5pt] \end{array}$

Mit dem Satz vom Nullprodukt folgt $k_1=0$ und $\frac{1}{3}\cdot k^2 -3=0.$

$\begin{array}[t]{rll} \frac{1}{3}\cdot k^2 -3 &=& 0 &\quad \scriptsize \mid\;+3 \\[5pt] \frac{1}{3}\cdot k^2 &=& 3 &\quad \scriptsize \mid\; \cdot 3\\[5pt] k^2&=& 9 &\quad \scriptsize \mid\; \sqrt{\;}\\[5pt] k_2 &=& -3 \\[5pt] k_3 &=& 3 \end{array}$

Für $k_1=0,$ $k_2=-3$ und $k_3 = 3$ ist $\displaystyle\int_{0}^{k}f(x)\;\mathrm dx =0.$

(2)

Das Integral beschreibt eine Flächenbilanz. Diese ist dann negativ, wenn mehr als die Hälfte der Fläche unterhalb der $x$ -Achse liegt und positive, wenn mehr als die Hälfte der Fläche oberhalb der $x$ -Achse liegt. Mit den Ergebnissen von oben und der Abbildung folgt also:

Für $0\lt k \lt 3$ ist $\displaystyle\int_{0}^{k}f(x)\;\mathrm dx \lt 0.$
Für $3\lt k$ ist $\displaystyle\int_{0}^{k}f(x)\;\mathrm dx \gt 0.$

(1)

Die Zufallsgröße $X$ ist binomialverteilt mit $n=10$ und $p=0,8$ . Folgende Diagramme stellen nicht die Wahrscheinlichkeitsverteilung von $X$ dar:

Diagramm 1 (Abbildung 3): Wegen $n=10$ kann die Wahrscheinlichkeit $P(X\gt 10)$ nicht größer als null sein.
Diagramm 3 (Abbildung 5): Bei einer binomialverteilten Zufallsvariable muss die Summe aller Wahrscheinlichkeiten genau $1$ ergeben. Die hier dargestellten Wahrscheinlichkeiten für $k=8$ und $k=9$ sind in Summe bereits größer als 1, deshalb ist hier keine Wahrscheinlichkeitsverteilung dargestellt.

(2)

Die Zufallsgröße $Y$ ist binomialverteilt, wobei die Wahrscheinlichkeitsverteilung von $Y$ symmetrisch ist. Damit folgt bereits der Parameter $p=0,5.$
Außerdem ist bekannt, dass der Erwartungswert von $Y$ 8 ist. Für den Erwartungswert gilt $E[Y]=n\cdot p$ . Einsetzen ergibt:

$\begin{array}[t]{rll} 8&=&n\cdot 0,5&\quad \scriptsize \mid\; \cdot2\\[5pt] 16&=&n \end{array}$

$Y$ ist binomialverteilt mit $n=16$ und $p=0,5$ .