Analysis 1
Aufgabe 1
Gegeben ist die inDie Abbildung zeigt die Graphen
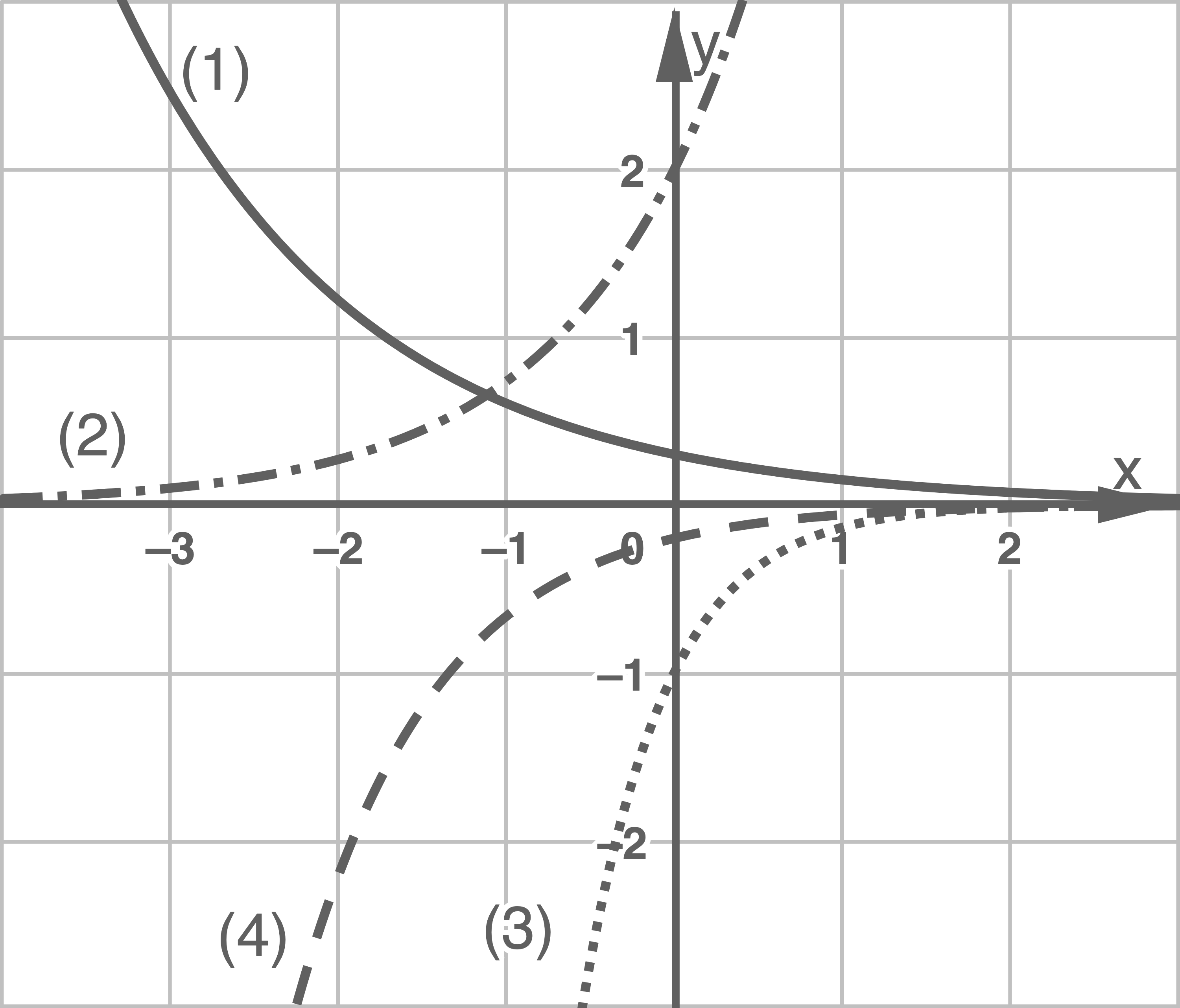
a)
Ordne den Graphen aus der Abbildung den passenden Parameterwert zu.
(3 Punkte)
b)
Gib an, für welche Werte von  die zugehörigen Funktionen
die zugehörigen Funktionen  streng monoton wachsend bzw. streng monoton fallend sind.
streng monoton wachsend bzw. streng monoton fallend sind.
(3 Punkte)
c)
Bestimme den Parameter  so, dass die Tangente an den Graphen
so, dass die Tangente an den Graphen  in seinem Schnittpunkt mit der
in seinem Schnittpunkt mit der  -Achse die Steigung 2 hat.
-Achse die Steigung 2 hat.
(2 Punkte)
d)
Ermittle die Gleichung der Gerade s, die zur Tangente an den Graphen  im Punkt
im Punkt  senkrecht verläuft.
senkrecht verläuft.
(2 Punkte)
e)
Gib begründet alle Werte von  an, bei denen die Gerade
an, bei denen die Gerade  mit dem Graphen
mit dem Graphen  der Funktion
der Funktion  genau einen Schnittpunkt gemeinsam hat.
genau einen Schnittpunkt gemeinsam hat.
Nun sei
(5 Punkte)
f)
Für  und
und  sei der Term
sei der Term 
 definiert.
Begründe, dass
definiert.
Begründe, dass  den Inhalt der Fläche, die der Graph
den Inhalt der Fläche, die der Graph  , die Koordinatenachsen und die Gerade
, die Koordinatenachsen und die Gerade  einschließen, angibt.
Zeige, dass dieser Flächeninhalt für
einschließen, angibt.
Zeige, dass dieser Flächeninhalt für 
 den Wert
den Wert  hat.
hat.
(6 Punkte)
g)
Bestimme den Parameter  so, dass der Inhalt der Fläche, die der Graph
so, dass der Inhalt der Fläche, die der Graph  und die
und die  -Achse im
-Achse im
2. Quadranten einschließen, mit dem Wert des Parameters übereinstimmt.
2. Quadranten einschließen, mit dem Wert des Parameters übereinstimmt.
(2 Punkte)
Aufgabe 2
In einem Modell wird die Querschnittsfläche eines 200
a)
Beschreibe den Einfluss der Parameter  und
und  auf die Graphen der Schar.
auf die Graphen der Schar.
(3 Punkte)
b)
Bestimme die Parameter  und
und  so, dass der Kanal die Breite 31,5
so, dass der Kanal die Breite 31,5  und die Tiefe 10
und die Tiefe 10  hat.
hat.
Wir betrachten nun die Funktion
(3 Punkte)
c)
Die Pegelhöhe des Kanals beträgt  Untersuche mithilfe einer geeigneten Rechnung und der Abbildung 2, wie weit sich eine Person, deren Augen sich in einer Höhe von
Untersuche mithilfe einer geeigneten Rechnung und der Abbildung 2, wie weit sich eine Person, deren Augen sich in einer Höhe von  befinden, maximal vom Ufer entfernen kann, um trotzdem die Wasserlinie des gegenüberliegenden Ufers sehen zu können.
befinden, maximal vom Ufer entfernen kann, um trotzdem die Wasserlinie des gegenüberliegenden Ufers sehen zu können.
(5 Punkte)
d)
Die Abbildung 3 stellt einen Lösungsansatz dar, mit dessen Hilfe die Pegelhöhe, zu der der Kanal mit der Hälfte der maximalen Wassermenge gefüllt ist, ermittelt werden soll. Nachfolgend werden Schritte einer rechnerischen Lösung dargestellt. Erläutere die einzelnen Lösungsschritte, ohne dabei die Zahlenwerte nachzurechnen!
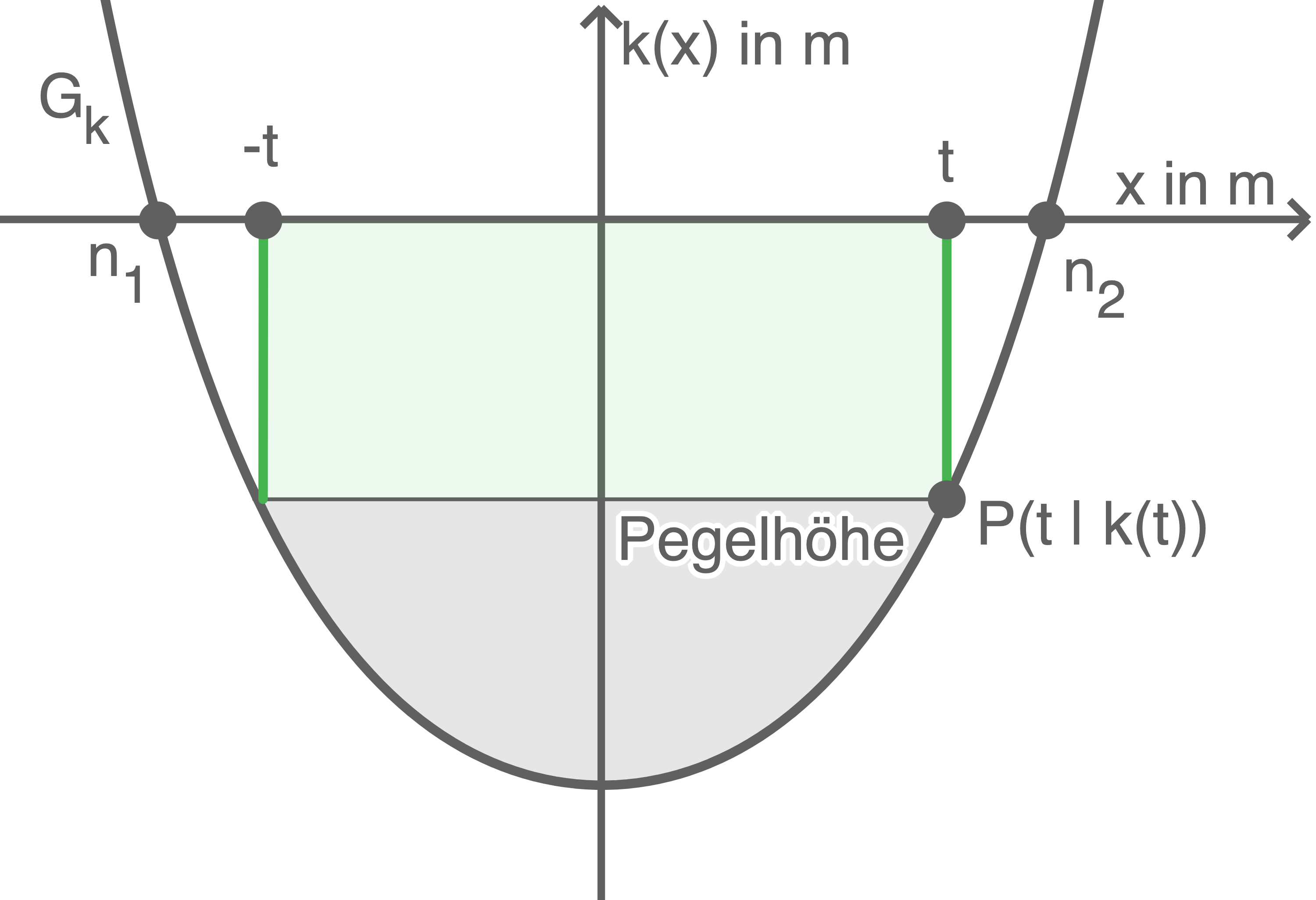






 Pegelhöhe ca. 6,1
Pegelhöhe ca. 6,1 

Abbildung 3
(1)
(2)
(3)
(4)
(5)
(6 Punkte)
(40 Punkte)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung 1
a)
Der Graph  verläuft monoton fallend über der
verläuft monoton fallend über der  -Achse. Der Parameter
-Achse. Der Parameter  muss folglich positiv sein und der Exponent der
muss folglich positiv sein und der Exponent der  -Funktion negativ. Dies ist von den möglichen Funktionen der Schar
-Funktion negativ. Dies ist von den möglichen Funktionen der Schar  nur für die Funktion mit
nur für die Funktion mit  erfüllt.
Es gilt
erfüllt.
Es gilt  Es handelt sich also um die mit dem Faktor
Es handelt sich also um die mit dem Faktor  gestreckte Exponentialfunktion, die folglich den
gestreckte Exponentialfunktion, die folglich den  -Achsenabschnitt 2 hat. Damit lässt sich der Graph
-Achsenabschnitt 2 hat. Damit lässt sich der Graph  der Funktion
der Funktion  zuordnen.
Es gilt
zuordnen.
Es gilt  Damit lässt sich der Graph
Damit lässt sich der Graph  eindeutig der Funktion
eindeutig der Funktion  zuordnen.
Nach dem Ausschlusskriterium lässt sich der Graph
zuordnen.
Nach dem Ausschlusskriterium lässt sich der Graph  nun der Funktion
nun der Funktion  zuordnen.
zuordnen.
b)
Für  ist
ist  streng monoton wachsend, da in diesem Fall die
streng monoton wachsend, da in diesem Fall die  -Funktion und auch das
-Funktion und auch das  im Exponenten einen positiven Vorfaktor haben.
Für
im Exponenten einen positiven Vorfaktor haben.
Für  ist
ist  streng monoton fallend, da die
streng monoton fallend, da die  -Funktion einen positiven und das
-Funktion einen positiven und das  im Exponenten einen negativen Vorfaktor hat.
Für
im Exponenten einen negativen Vorfaktor hat.
Für  ist
ist  wieder streng monoton wachsend, da in diesem Fall die
wieder streng monoton wachsend, da in diesem Fall die  -Funktion und auch das
-Funktion und auch das  im Exponenten einen negativen Vorfaktor haben.
im Exponenten einen negativen Vorfaktor haben.
c)
Damit die Tangente an den Graphen  in seinem Schnittpunkt mit der
in seinem Schnittpunkt mit der  -Achse die Steigung
-Achse die Steigung  hat, muss
hat, muss  gelten.
gelten.

 Gesucht ist also die Lösung der Gleichung
Gesucht ist also die Lösung der Gleichung 
![\(\begin{array}[t]{rll}
a\cdot (a-1)&=& 2 \\
a^2-a&=& 2 &\quad \scriptsize \mid\; -2 \\[5pt]
a^2-a-2&=& 0
\end{array}\)](https://mathjax.schullv.de/bc545f4d3b20890d8358cbc1d156bde4ae7976344a03f3eff5662663394ebced?color=5a5a5a) Mit der pq-Formel folgt:
Mit der pq-Formel folgt:



d)
Gesucht ist eine Gerade  die senkrecht zur Tangente an
die senkrecht zur Tangente an  im Punkt
im Punkt  verläuft.
verläuft.
 berechnen
Die Steigung der Tangenten an
berechnen
Die Steigung der Tangenten an  an der Stelle
an der Stelle  ist gegeben durch
ist gegeben durch  Die Steigung
Die Steigung  der Geraden
der Geraden  lässt sich berechnen durch
lässt sich berechnen durch 
 berechnen
Da
berechnen
Da  außerdem den Punkt
außerdem den Punkt  enthalten muss, muss
enthalten muss, muss  gelten.
gelten.
![\(\begin{array}[t]{rll}
s(x)&=& -\dfrac{1}{2}x+c \\[5pt]
s(0)&=& -\dfrac{1}{2}\cdot 0+c =c\\[5pt]
\end{array}\)](https://mathjax.schullv.de/fd0c4a5f1c0091aee7b5dcfae6dc313007b7e6c566cafd548b91e9723f649bd7?color=5a5a5a) Es gilt also
Es gilt also  und damit
und damit 
e)
Für  ist
ist  streng monoton fallend, während
streng monoton fallend, während  streng monoton wachsend ist (siehe Teilaufgabe b). Folglich hat die Gerade mit der Funktion nur einen Schnittpunkt.
Für
streng monoton wachsend ist (siehe Teilaufgabe b). Folglich hat die Gerade mit der Funktion nur einen Schnittpunkt.
Für  nimmt
nimmt  konstant den Wert
konstant den Wert  an. Da
an. Da  streng monoton wachsend ist, hat die Funktion mit der Geraden auch hier nur einen Schnittpunkt.
Für
streng monoton wachsend ist, hat die Funktion mit der Geraden auch hier nur einen Schnittpunkt.
Für  sind sowohl
sind sowohl  als auch
als auch  streng monoton wachsend. Es gibt also nur dann genau einen Schnittpunkt, wenn
streng monoton wachsend. Es gibt also nur dann genau einen Schnittpunkt, wenn  eine Tangente an
eine Tangente an  ist. Da sowohl
ist. Da sowohl  als auch
als auch  den
den  -Achsenabschnitt
-Achsenabschnitt  haben, ist
haben, ist  eine Tangente an
eine Tangente an  wenn die Gerade an der Stelle
wenn die Gerade an der Stelle  außerdem die gleiche Steigung wie die Funktion
außerdem die gleiche Steigung wie die Funktion  hat. Wegen
hat. Wegen  hat
hat  also auch für
also auch für  genau einen Schnittpunkt mit
genau einen Schnittpunkt mit  gemeinsam.
gemeinsam.
f)
Begründen, dass  den beschriebenen Flächeninhalt angibt
Für
den beschriebenen Flächeninhalt angibt
Für  gilt
gilt  für alle
für alle  Damit ist der Inhalt der Fläche zwischen dem Graphen
Damit ist der Inhalt der Fläche zwischen dem Graphen  , der
, der  -Achse und den Geraden
-Achse und den Geraden  und
und  gegeben durch
gegeben durch 
 ist eine Stammfunktion von
ist eine Stammfunktion von  Weiter gilt
Weiter gilt  .
Damit ergibt sich:
.
Damit ergibt sich:

 Flächeninhalt für
Flächeninhalt für  Für
Für  und
und  gilt:
gilt:
g)
Nach Teilaufgabe f ist der gesuchte Flächeninhalt durch  gegeben. Gesucht ist also die Lösung der Gleichung
gegeben. Gesucht ist also die Lösung der Gleichung 
![\(\begin{array}[t]{rll}
\dfrac{a}{a-1}&=& a \quad \scriptsize \mid\; \cdot (a-1)\\[5pt]
a&=& a\cdot (a-1) \quad \scriptsize \mid\; :a\\[5pt]
1&=& a-1 \quad \scriptsize \mid\; +1 \\[5pt]
2&=& a \\[5pt]
a&=&2
\end{array}\)](https://mathjax.schullv.de/dbabf08709d9e23bf6429518f114513874875a2120c284127ff939584e35d12b?color=5a5a5a) Der gesuchte Wert ist
Der gesuchte Wert ist 
Aufgabe 2
a)
Der Parameter  streckt bzw. staucht den Graphen in
streckt bzw. staucht den Graphen in  -Richtung.
-Richtung.
 Der Graph hat einen Hochpunkt und verläuft rechtsgekrümmt.
Der Graph hat einen Hochpunkt und verläuft rechtsgekrümmt.
 Der Graph hat einen Tiefpunkt und verläuft linksgekrümmt.
Der Parameter
Der Graph hat einen Tiefpunkt und verläuft linksgekrümmt.
Der Parameter  verschiebt den Graphen entlang der
verschiebt den Graphen entlang der  -Achse.
-Achse.
b)
Es gilt 

 Damit ist
Damit ist  symmetrisch zur
symmetrisch zur  -Achse. Der Abstand von der
-Achse. Der Abstand von der  -Achse zum Rand des Kanals muss also auf beiden Seiten
-Achse zum Rand des Kanals muss also auf beiden Seiten ![\(\dfrac{31,5}{2}=15,75\,\text{[m]}\)](https://mathjax.schullv.de/db0af3e32c537cb9f92d5819d01535f9bc87a7dea87f2e8b06cc048e29143ddc?color=5a5a5a) betragen. Außerdem liegt der tiefste Punkt des Kanals auf der
betragen. Außerdem liegt der tiefste Punkt des Kanals auf der  -Achse.
Das zu lösende Gleichungssystem ergibt sich nun aus den folgenden Bedingungen:
Mit dem Taschenrechner folgt
-Achse.
Das zu lösende Gleichungssystem ergibt sich nun aus den folgenden Bedingungen:
Mit dem Taschenrechner folgt  und
und 
c)
Der Punkt  befindet sich auf der Kante des Ufers. Die Gerade
befindet sich auf der Kante des Ufers. Die Gerade  verläuft im Querschnitt des Kanals durch die Punkte
verläuft im Querschnitt des Kanals durch die Punkte  und
und  welcher auf der Wasserlinie der gegenüberliegenden Seite liegt.
Da der Kanal
welcher auf der Wasserlinie der gegenüberliegenden Seite liegt.
Da der Kanal  tief ist und die Pegelhöhe
tief ist und die Pegelhöhe  beträgt, befindet sich die Wasserlinie in den sieben Metern Tiefe. Die Koordinaten des Punktes
beträgt, befindet sich die Wasserlinie in den sieben Metern Tiefe. Die Koordinaten des Punktes  ergeben sich somit aus der Gleichung
ergeben sich somit aus der Gleichung  wobei
wobei  sein muss. Mit dem Taschenrechner folgt
sein muss. Mit dem Taschenrechner folgt  also
also 
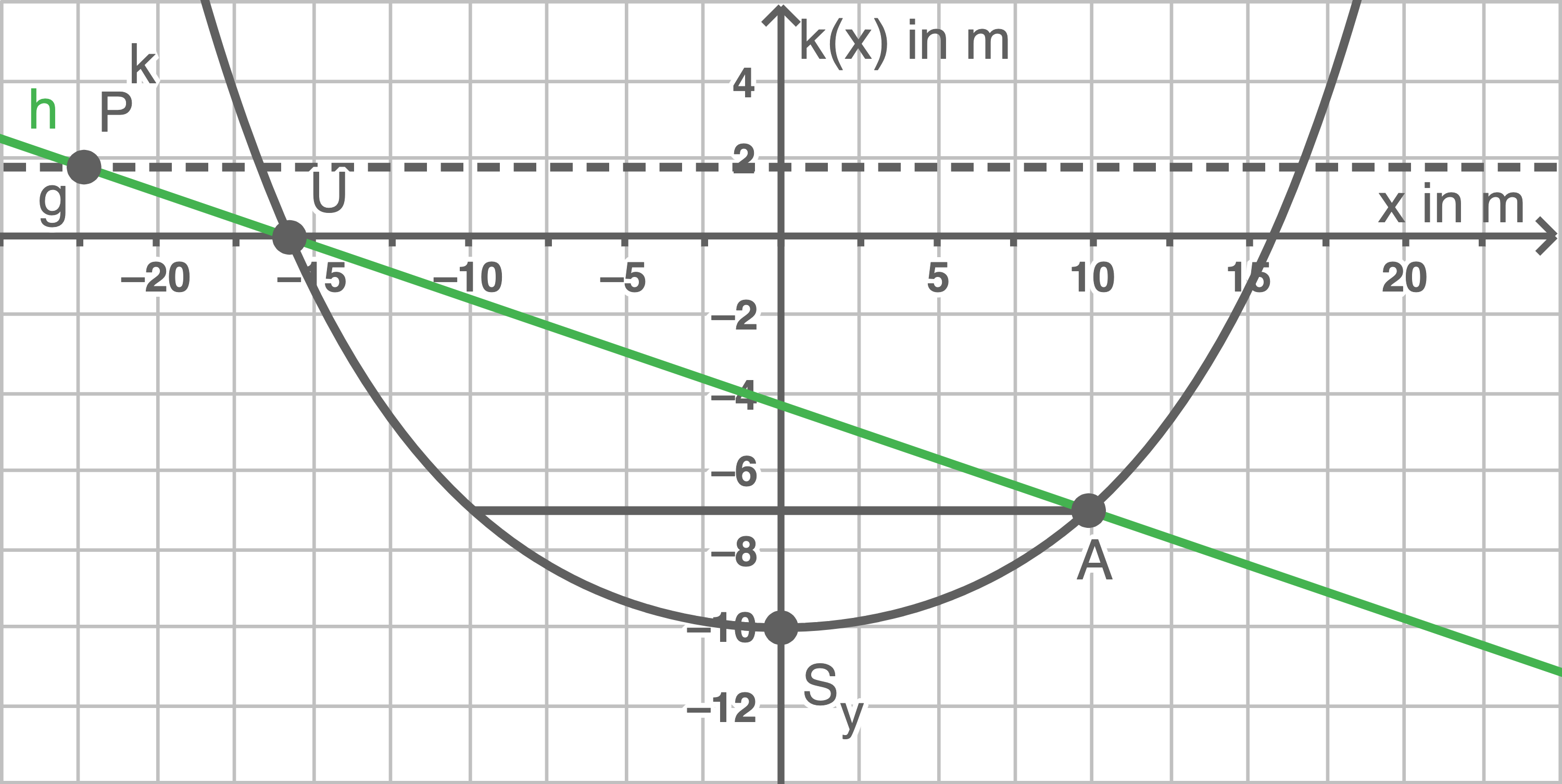
Skizze
d)
Zur Ermittlung der entsprechenden Pegelhöhe genügt die Betrachtung der Querschnittsfäche des Kanals.
(1) und (2):
Die hellschraffierte Fläche ist die linke Seite bei (1) und stellt die Querschnittsfläche des Kanals bei halber Füllung dar. Sie ergibt sich aus der Differenz der gesamten Fläche im Intervall![\([-t ; t]\)](https://mathjax.schullv.de/78a7f87e8f46a3d73988feb131aa333794a1b02460605a80f8aa210d527386d2?color=5a5a5a) und dem grün schraffierten Rechteck. Sie soll halb so groß sein wie die gesamte Querschnittsfläche des Kanals, also
und dem grün schraffierten Rechteck. Sie soll halb so groß sein wie die gesamte Querschnittsfläche des Kanals, also  .
(3):
.
(3):
Es genügt aus Symmetriegründen, die Fläche im Intervall![\([0 ; t]\)](https://mathjax.schullv.de/4d9d03e4e85baa3100c8e477e388093da7e02000f757f83e45582b5a3f8710a5?color=5a5a5a) zu betrachten.
(4):
zu betrachten.
(4):
Es wird nun die Stammfunktion von eingesetzt. Anschließend wird die Lösung der entstehenden Gleichung ermittelt.
(5):
eingesetzt. Anschließend wird die Lösung der entstehenden Gleichung ermittelt.
(5):
Der -Wert des Punktes
-Wert des Punktes  wird berechnet. Die Pegelhöhe ergibt sich schließlich als Differenz dieses Wertes und des
wird berechnet. Die Pegelhöhe ergibt sich schließlich als Differenz dieses Wertes und des  -Achsenabschnittes der Funktion
-Achsenabschnittes der Funktion  .
.
Die hellschraffierte Fläche ist die linke Seite bei (1) und stellt die Querschnittsfläche des Kanals bei halber Füllung dar. Sie ergibt sich aus der Differenz der gesamten Fläche im Intervall
Es genügt aus Symmetriegründen, die Fläche im Intervall
Es wird nun die Stammfunktion von
Der