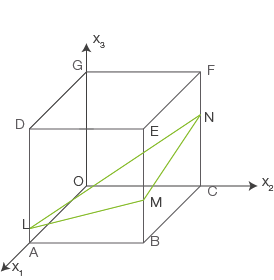
Aufgabe 3
Aufgabenstellung
In einem kartesischen Koordinatensystem sind die Punkte  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  und
und  Eckpunkte eines Würfels
Eckpunkte eines Würfels  . Außerdem sind die Punkte
. Außerdem sind die Punkte  ,
,  und
und  gegeben (siehe Abbildung).
gegeben (siehe Abbildung).








 Bildnachweise [nach oben]
Bildnachweise [nach oben]
a)
(1)
Zeige, dass das Dreieck  gleichschenklig ist.
gleichschenklig ist.
(4P)
(2)
Zeige, dass das Dreieck  nicht rechtwinklig ist.
nicht rechtwinklig ist.
(4P)
(3)
Bestimme den Flächeninhalt des Dreiecks  .
.
[Zur Kontrolle: Der Flächeninhalt des Dreiecks beträgt
beträgt  ].]
].]
[Zur Kontrolle: Der Flächeninhalt des Dreiecks
(5P)
b)
(1)
Ermittle eine Parameter- und eine Koordinatengleichung der Ebene  , die die Punkte
, die die Punkte  ,
,  und
und  enthält.
enthält.
[Mögliches Ergebnis für die Koordinatengleichung: .]
.]
[Mögliches Ergebnis für die Koordinatengleichung:
(7P)
(2)
Bestimme das Volumen der Pyramide  .
.
[Zur Kontrolle: Das Volumen der Pyramide beträgt
beträgt 
![\(\big[VE\big]\)](https://mathjax.schullv.de/19e4011c4fa3f17f9b2e2f03cb157d7b27a9810f8fac74ad3ed183d529499b71?color=5a5a5a) .]
.]
[Zur Kontrolle: Das Volumen der Pyramide
(6P)
(3)
Berechne, wie viel Prozent des Würfelvolumens das Pyramidenvolumen einnimmt.
(3P)
c)
(1)
Skizziere in der Abbildung das Schnittgebilde, das die Ebene  mit dem Würfel bildet.
mit dem Würfel bildet.
(3P)
Das Schnittgebilde von Ebene und Würfel ist ein Raute.
(2)
Untersuche, ob der Punkt  in der Raute liegt.
in der Raute liegt.
(3P)
(3)
Untersuche, ob es einen Punkt auf der Geraden  gibt, der von dem Punkt
gibt, der von dem Punkt  den Abstand
den Abstand 
![\([\text{LE}]\)](https://mathjax.schullv.de/d5a2254067b35a8eb9a58764cb01b6fccf536523302989b91bc49ae3bf6cf7e1?color=5a5a5a) besitzt.
besitzt.
(7P)
d)
Es gibt genau eine Gerade  durch
durch  , die die Geraden
, die die Geraden  und
und  (außerhalb des Würfels) schneidet.
(außerhalb des Würfels) schneidet.
(1)
Begründe, dass die Gerade  in der Ebene
in der Ebene  liegt.
liegt.
(4P)
(2)
Bestimme die Koordinaten eines zweiten Punktes der Geraden  .
.
(4P)
© 2016 - SchulLV.
a)
(1)
menu  7: Matrix und Vektor
7: Matrix und Vektor  7: Normen
7: Normen  1: Norm
1: Norm
Den Vektor kannst du mit folgendem Befehl einfügen:
menu  7: Matrix und Vektor
7: Matrix und Vektor  1: Erstellen...
1: Erstellen...  1: Matrix...
1: Matrix...
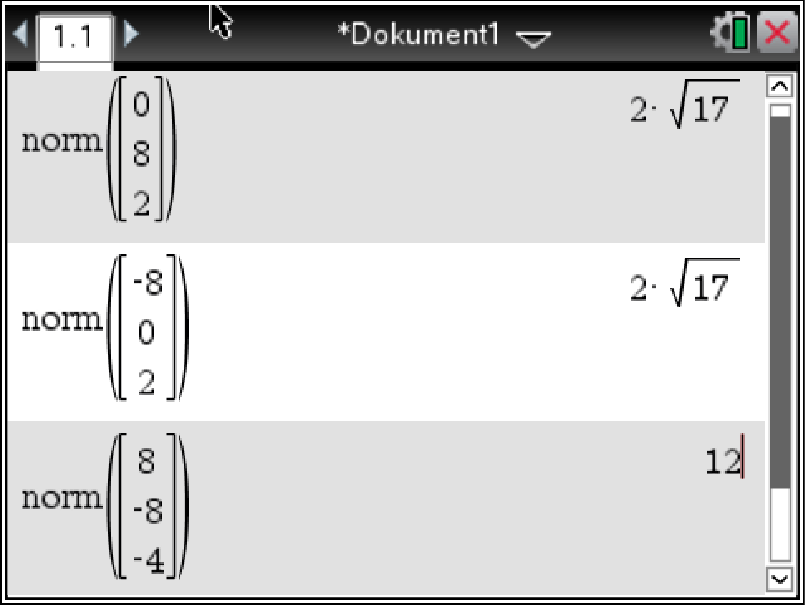 Abb. 1: Betrag der Vektoren berechnen.
Abb. 1: Betrag der Vektoren berechnen.
(2)
menu  7: Matrix und Vektor
7: Matrix und Vektor  C: Vektor
C: Vektor  3: Skalarprodukt
3: Skalarprodukt
Mit dem gleichen Befehl wie oben kannst du die Vektoren einsetzen.
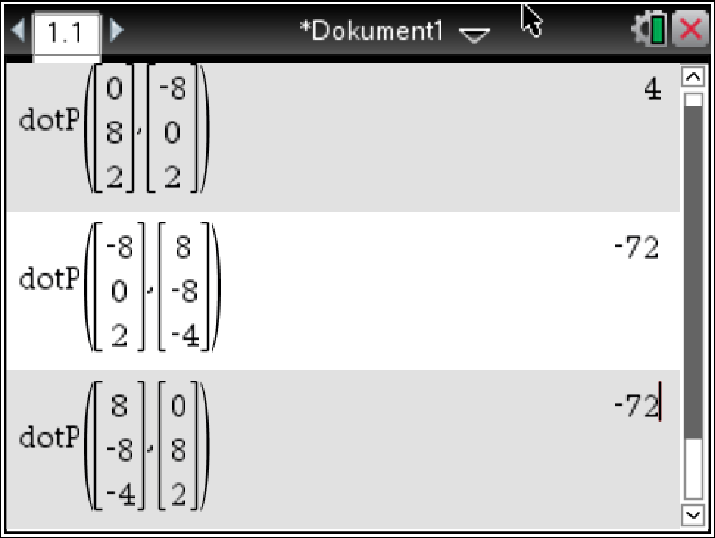 Abb. 2: Skalarprodukt berechnen.
Abb. 2: Skalarprodukt berechnen.
(3)
Das Vektorprodukt kannst du mit deinem Taschenrechner berechnen.
menu  7: Matrix und Vektor
7: Matrix und Vektor  C: Vektor
C: Vektor  2: Kreuzprodukt
2: Kreuzprodukt
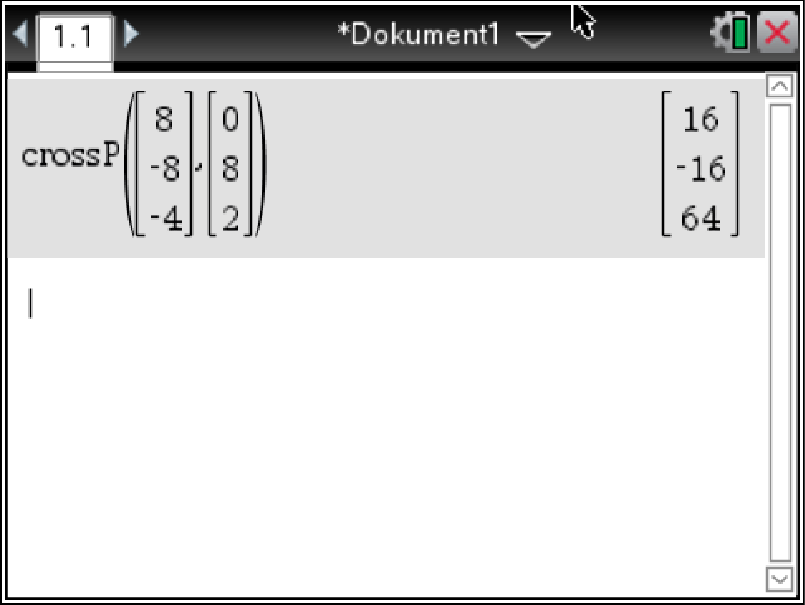 Abb. 3: Kreuzprodukt berechnen.
Abb. 3: Kreuzprodukt berechnen.
b)
(1)
menu  7: Matrix und Vektor
7: Matrix und Vektor  C: Vektor
C: Vektor  2: Kreuzprodukt
2: Kreuzprodukt
 Abb. 4: Kreuzprodukt berechnen.
Abb. 4: Kreuzprodukt berechnen.
(2)
(3)
c)
(1)
menu  3: Algebra
3: Algebra  7: Gleichungssystem lösen
7: Gleichungssystem lösen  1: Gleichungssytsem lösen...
1: Gleichungssytsem lösen...
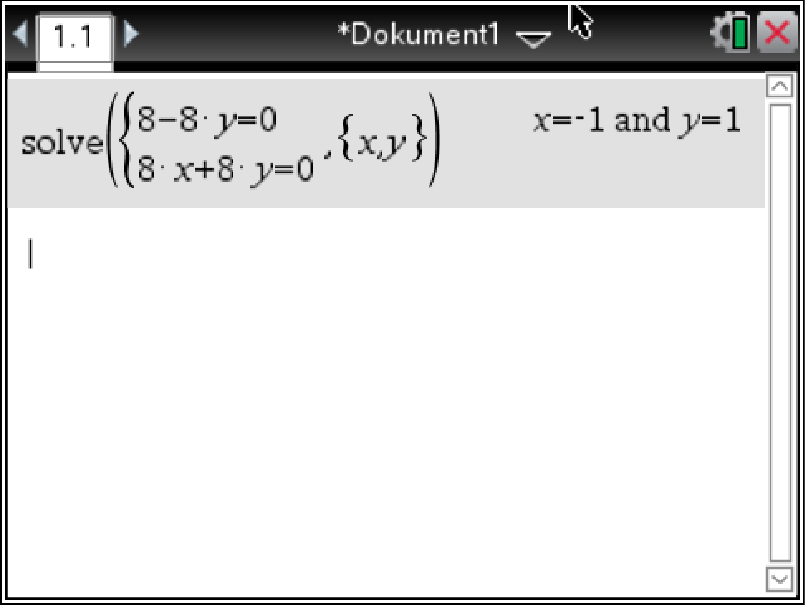 Abb. 5: Gleichung lösen.
Abb. 5: Gleichung lösen.
Wenn du jetzt die berechneten Werte für  und
und  in die dritte Zeile der Ebenengleichung einsetzt, erhälst du die Koordinaten des Schnittpunktes
in die dritte Zeile der Ebenengleichung einsetzt, erhälst du die Koordinaten des Schnittpunktes  .
.
 Die Koordinaten des Punktes
Die Koordinaten des Punktes  lauten
lauten  .
Diesen Punkt kannst du nun in das gegebene Koordinatensystem einzeichnen, und anschließend die Eckpunkte
.
Diesen Punkt kannst du nun in das gegebene Koordinatensystem einzeichnen, und anschließend die Eckpunkte  und
und  mit dem Punkt
mit dem Punkt  verbinden.
verbinden.
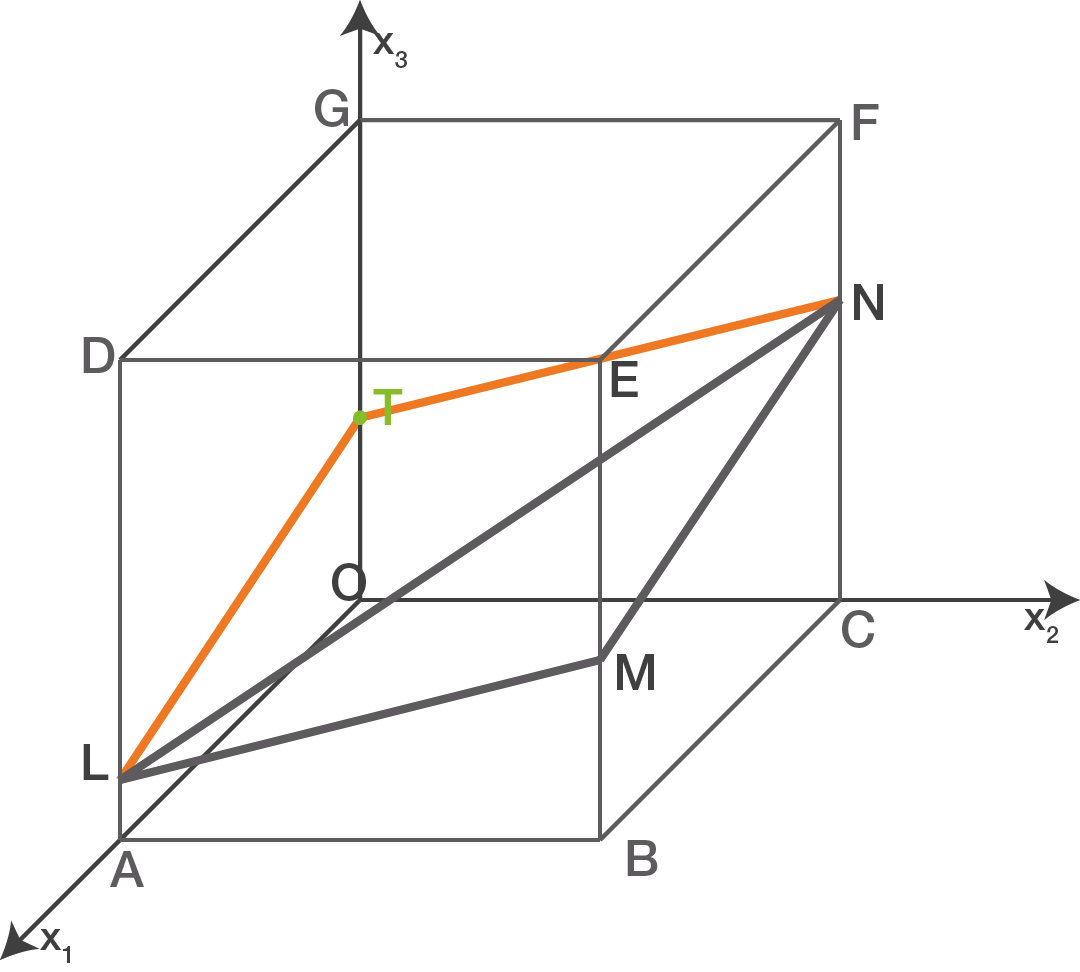 Abb. 6: Skizze Schnittgebilde
Abb. 6: Skizze Schnittgebilde
(2)
(3)
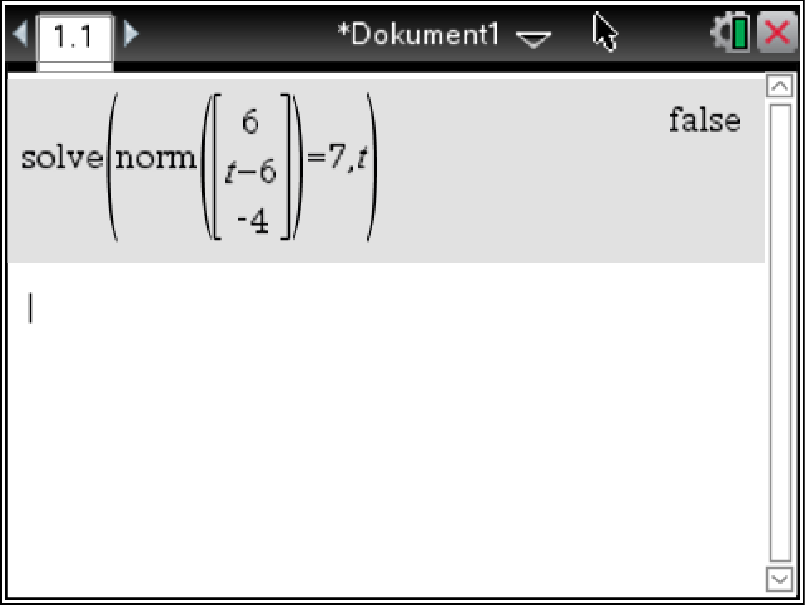 Abb. 7: Gleichung lösen.
Abb. 7: Gleichung lösen.
d)
(1)
(2)
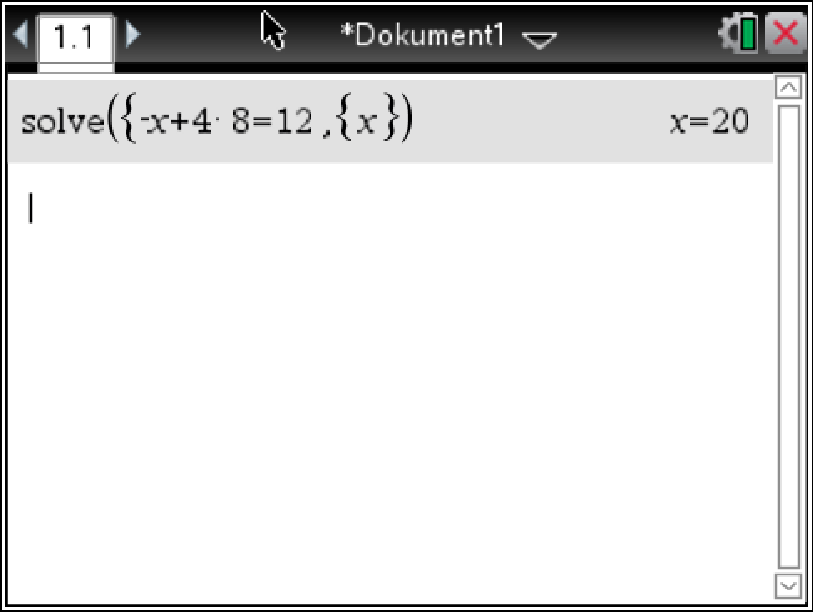 Abb. 8: Gleichung lösen.
Abb. 8: Gleichung lösen.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
a)
(1)
Keyboard  Math2
Math2
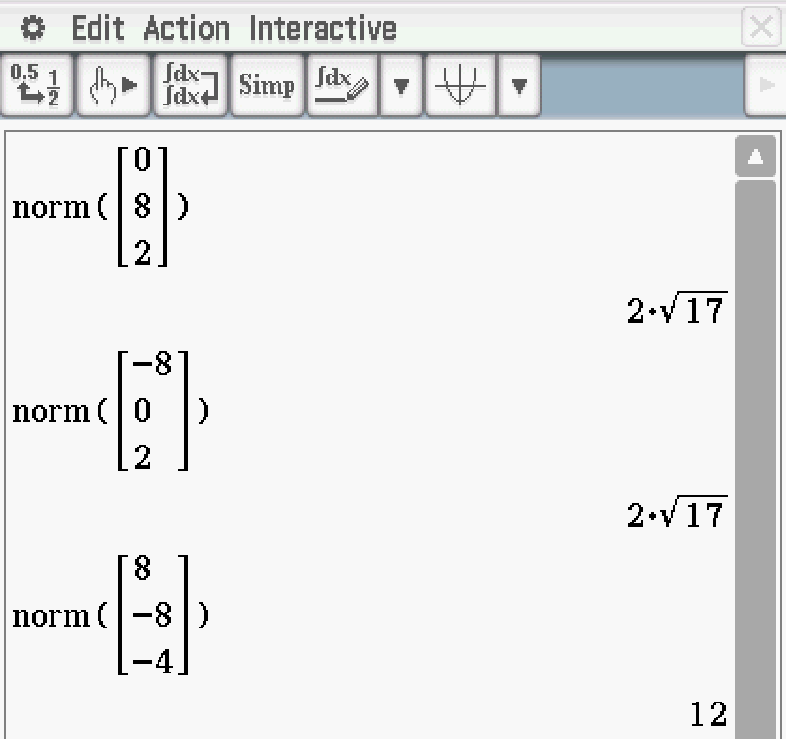 Abb. 1: Betrag der Vektoren berechnen.
Abb. 1: Betrag der Vektoren berechnen.
(2)
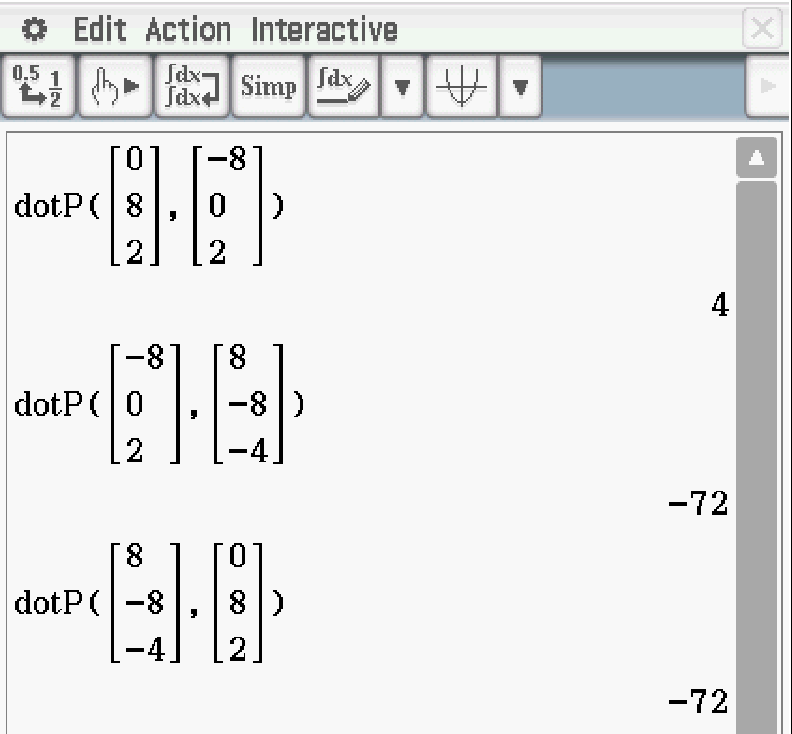 Abb. 2: Skalarprodukt berechnen.
Abb. 2: Skalarprodukt berechnen.
(3)
Das Vektorprodukt kannst du mit dem crossP-Befehl berechnen.
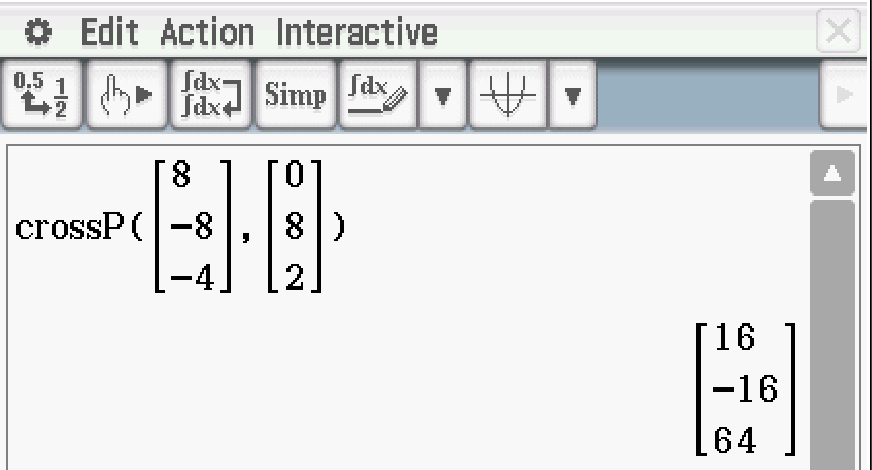 Abb. 3: Kreuzprodukt berechnen.
Abb. 3: Kreuzprodukt berechnen.
b)
(1)
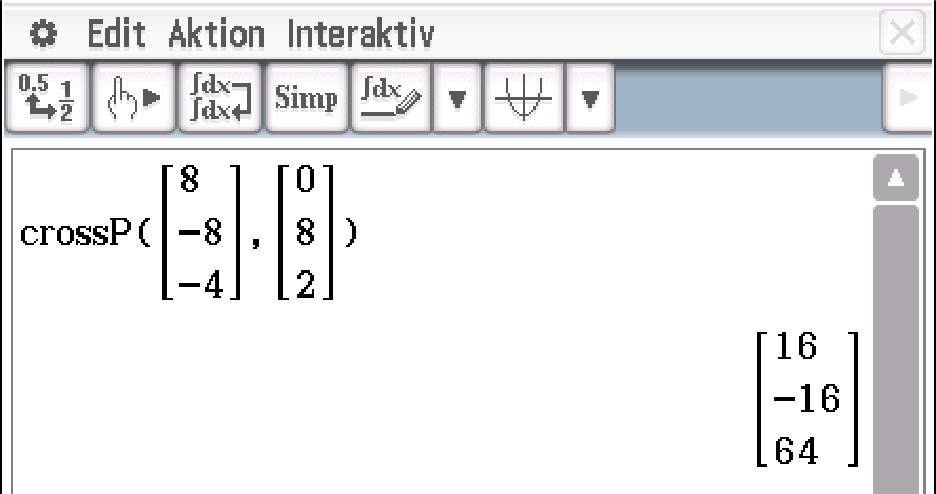 Abb. 4: Kreuzprodukt berechnen.
Abb. 4: Kreuzprodukt berechnen.
(2)
(3)
c)
(1)
Keyboard  Math1
Math1
 Abb. 5: Gleichung lösen.
Abb. 5: Gleichung lösen.
Wenn du jetzt die berechneten Werte für  und
und  in die dritte Zeile der Ebenengleichung einsetzt, erhälst du die Koordinaten des Schnittpunktes
in die dritte Zeile der Ebenengleichung einsetzt, erhälst du die Koordinaten des Schnittpunktes  .
.
 Die Koordinaten des Punktes
Die Koordinaten des Punktes  lauten
lauten  .
Diesen Punkt kannst du nun in das gegebene Koordinatensystem einzeichnen, und anschließend die Eckpunkte
.
Diesen Punkt kannst du nun in das gegebene Koordinatensystem einzeichnen, und anschließend die Eckpunkte  und
und  mit dem Punkt
mit dem Punkt  verbinden.
verbinden.
 Abb. 6: Skizze Schnittgebilde
Abb. 6: Skizze Schnittgebilde
(2)
(3)
 Abb. 7: Gleichung lösen.
Abb. 7: Gleichung lösen.
d)
(1)
(2)
 Abb. 6: Skizze Schnittgebilde
Abb. 6: Skizze Schnittgebilde
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.