Aufgabe 3
Die Abbildung zeigt den Würfel  mit
mit  und
und  in einem kartesischen Koordinatensystem. Die Ebene
in einem kartesischen Koordinatensystem. Die Ebene  schneidet die Kanten des Würfels unter anderem in den Punkten
schneidet die Kanten des Würfels unter anderem in den Punkten 

 und
und 
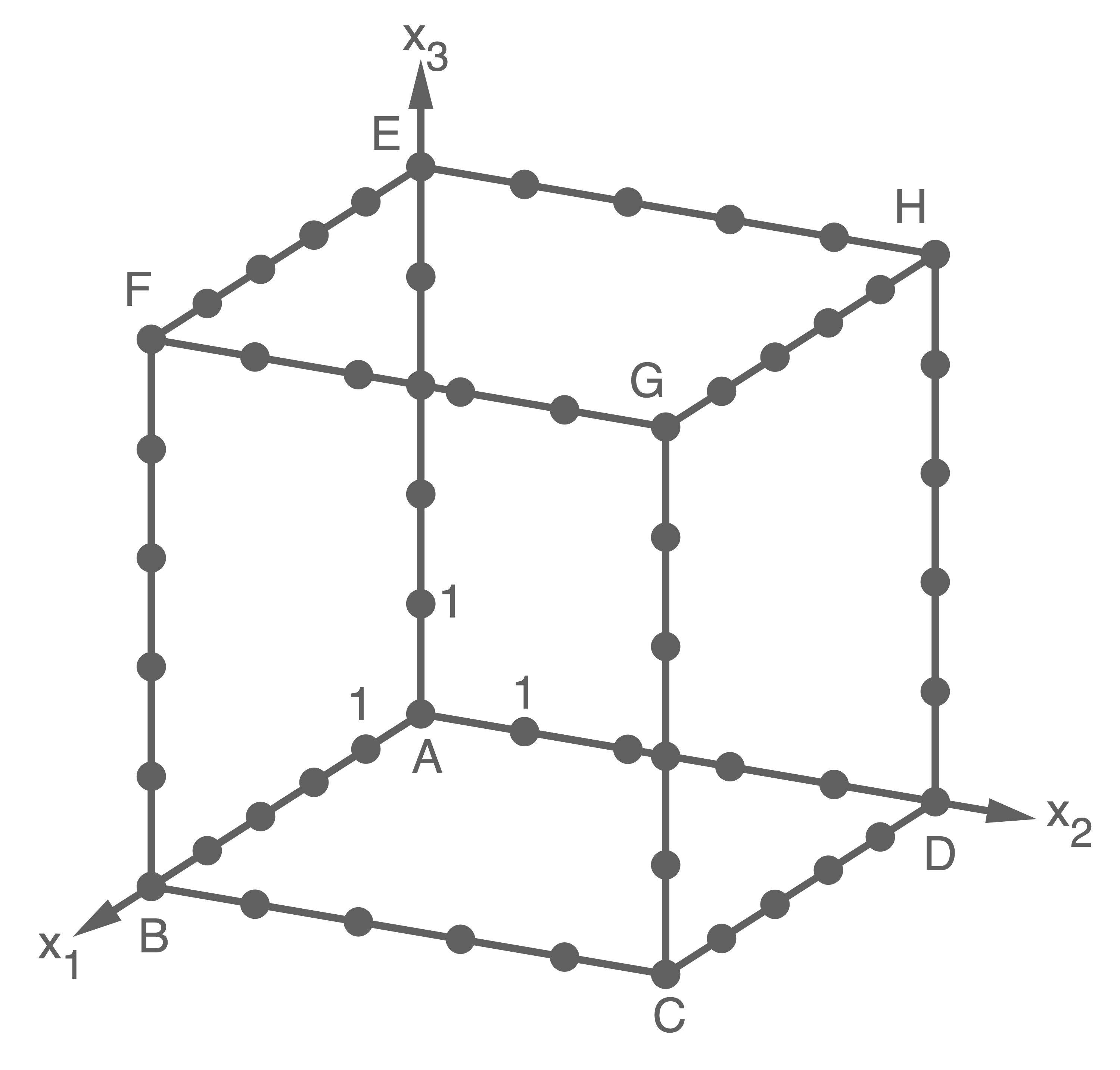
Abbildung
a)
Zeichne das Viereck  in die Abbildung ein.
in die Abbildung ein.
(4 Punkte)
b)
Zeige, dass das Viereck ein Trapez ist, bei dem zwei Seiten gleich lang sind.
(4 Punkte)
c)
Der Punkt  liegt auf der Strecke
liegt auf der Strecke 
Zeige, dass auf
auf  senkrecht steht.
Bestimme rechnerisch den Flächeninhalt des Trapezes
senkrecht steht.
Bestimme rechnerisch den Flächeninhalt des Trapezes  [Zur Kontrolle: Der Flächeninhalt beträgt
[Zur Kontrolle: Der Flächeninhalt beträgt  ]
]
Zeige, dass
(7 Punkte)
d)
Ermittle eine Gleichung der Ebene  in Koordinatenform.
in Koordinatenform.
[Zur Kontrolle: ]
]
Der Abstand [Zur Kontrolle:
(5 Punkte)
e)
Bestimme das Volumen einer Pyramide mit der Grundfläche  und der Spitze
und der Spitze 
(4 Punkte)
f)
Die Spitze einer Pyramide mit der Grundfläche  liegt auf der Strecke
liegt auf der Strecke  .
.
Untersuche, ob die Höhe dieser Pyramide betragen kann.
betragen kann.
Spiegelt man Untersuche, ob die Höhe dieser Pyramide
(5 Punkte)
g)
Berechne die Größe des Winkels, unter dem sich  und
und  schneiden.
schneiden.
Betrachtet wird die Schar der Geraden
(3 Punkte)
h)
Begründe, dass keine Gerade der Schar in der Ebene mit der Gleichung  liegt.
liegt.
(2 Punkte)
i)
Bestimme eine Parametergleichung der Geraden  die zur Schar
die zur Schar  gehört und in der Ebene
gehört und in der Ebene  liegt.
liegt.
Zeige, dass die Gerade auch in
auch in  liegt.
liegt.
Zeige, dass die Gerade
(6 Punkte)
a)
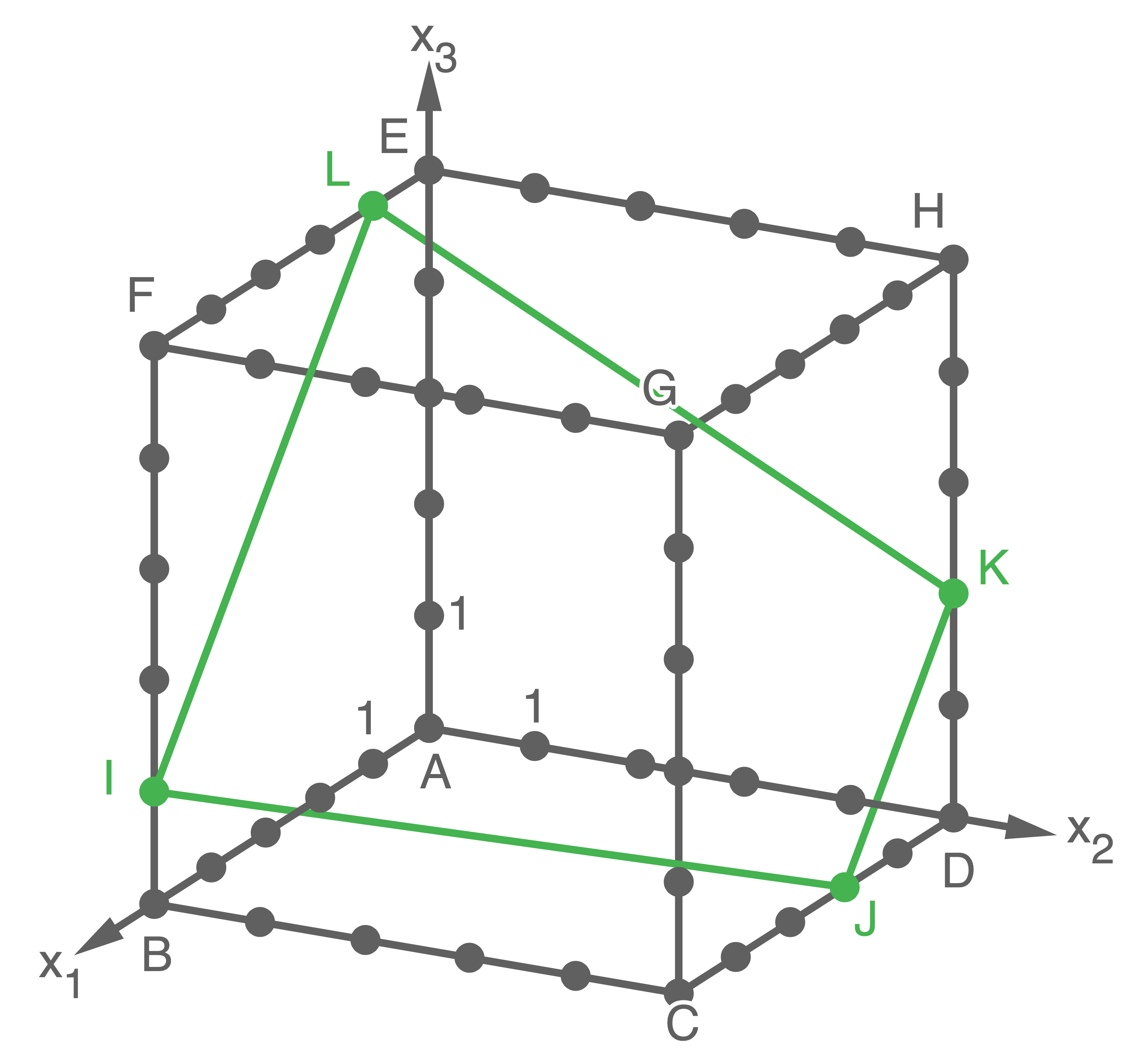
b)
In der Abbildung von oben kannst ist erkennbar, dass die beiden parallelen Seiten des Trapezes vermutlich die beiden Seiten  und
und  sind. Für die zugehörigen Verbindungsvektoren folgt:
sind. Für die zugehörigen Verbindungsvektoren folgt:
![\(\begin{array}[t]{rll}
\overrightarrow{LI} &=& \pmatrix{4\\0\\-4} \\[5pt]
\overrightarrow{KJ} &=& \pmatrix{2\\0\\-2}
\end{array}\)](https://mathjax.schullv.de/106aae96f727342e3877bc56c4905a1a8813dc5a9450faf28c37026aa53bae47?color=5a5a5a) Es gilt
Es gilt  Die beiden Vektoren
Die beiden Vektoren  und
und  sind also linear abhängig und damit parallel zueinander. Daher sind auch die zugehörigen Vierecksseiten
sind also linear abhängig und damit parallel zueinander. Daher sind auch die zugehörigen Vierecksseiten  und
und  parallel zueinander. Es handelt sich bei dem Viereck
parallel zueinander. Es handelt sich bei dem Viereck  daher um ein Trapez.
daher um ein Trapez.
Gefordert ist nun noch zu zeigen, dass zwei Seiten gleich lang sind.![\(\begin{array}[t]{rll}
\overline{LK}&=& \left|\overrightarrow{LK} \right| \\[5pt]
&=& \left|\pmatrix{-1\\5\\-3} \right| \\[5pt]
&=& \sqrt{(-1)^2 + 5^2 + (-3)^2} \\[5pt]
&=& \sqrt{35} \\[10pt]
\overline{IJ}&=& \left|\overrightarrow{IJ} \right| \\[5pt]
&=& \left|\pmatrix{-3\\5\\-1} \right| \\[5pt]
&=& \sqrt{(-3)^2 + 5^2 + (-1)^2} \\[5pt]
&=& \sqrt{35} \\[10pt]
\end{array}\)](https://mathjax.schullv.de/67a6bd4aef8528eafe1ddb63ebac5b1877382fe4ed4af7553505f6e5bc219ea3?color=5a5a5a) Es ist also
Es ist also  Somit ist Viereck
Somit ist Viereck  ein Trapez, bei dem zwei Seiten gleich lang sind.
ein Trapez, bei dem zwei Seiten gleich lang sind.
Gefordert ist nun noch zu zeigen, dass zwei Seiten gleich lang sind.
c)
d)
e)
Die Höhe der Pyramide entspricht dem Abstand des Punktes  zur Ebene
zur Ebene  Es ist
Es ist 
 Die Grundfläche der Pyramide ist das Trapez
Die Grundfläche der Pyramide ist das Trapez  ihr Flächeninhalt ist also:
ihr Flächeninhalt ist also:
 Damit folgt für das Volumen:
Damit folgt für das Volumen:
![\(\begin{array}[t]{rll}
V &=& \frac{1}{3} \cdot G\cdot h \\[5pt]
&=& \frac{1}{3} \cdot 3\cdot \sqrt{66}\cdot\dfrac{20}{\sqrt{66}} \\[5pt]
&=& 20
\end{array}\)](https://mathjax.schullv.de/4616697de90d65938896a1c95f81305edad598a61c079c8b42e1ad12c5d375b9?color=5a5a5a) Das Volumen der Pyramide mit der Grundfläche
Das Volumen der Pyramide mit der Grundfläche  und der Spitze
und der Spitze  beträgt
beträgt 
f)
Die Pyramide kann also nicht die Höhe
g)
Mit den Normalenvektoren  und
und  folgt für den Schnittwinkel
folgt für den Schnittwinkel 
![\(\begin{array}[t]{rll}
\cos (\alpha) &=& \dfrac{\left| \overrightarrow{n}_{T} \circ \overrightarrow{n}_{T‘} \right|}{\left| \overrightarrow{n}_{T} \right|\cdot \left| \overrightarrow{n}_{T‘} \right|} \\[5pt]
\cos (\alpha) &=& \dfrac{\left| \pmatrix{5\\4\\5} \circ \pmatrix{-5\\4\\5} \right|}{\left| \pmatrix{5\\4\\5} \right|\cdot \left| \pmatrix{-5\\4\\5} \right|} \\[5pt]
\cos (\alpha) &=& \dfrac{16}{\sqrt{66}\cdot \sqrt{66}} \\[5pt]
\cos (\alpha) &=& \dfrac{8}{33} \\[5pt]
\alpha &\approx& 76,0^{\circ}
\end{array}\)](https://mathjax.schullv.de/923dd3990c0fc99c84bb0c2be213e42995ddc80dde2e3e9c842a97112a5cb1b9?color=5a5a5a)
 und
und  schneiden sich unter einem Winkel mit der Größe von ca.
schneiden sich unter einem Winkel mit der Größe von ca. 
h)
Damit eine Gerade in der Ebene mit der Gleichung  liegt, muss die
liegt, muss die  -Koordinate jedes Punktes auf dieser Geraden
-Koordinate jedes Punktes auf dieser Geraden  sein. Dazu muss die
sein. Dazu muss die  -Koordinate des Richtungsvektors Null sein.
-Koordinate des Richtungsvektors Null sein.
Bei der Geradenschar ist die
ist die  -Koordinate des Richtungsvektors
-Koordinate des Richtungsvektors  Diese kann also in keinem Fall Null werden. Daher liegt keine der Geraden
Diese kann also in keinem Fall Null werden. Daher liegt keine der Geraden  in der Ebene mit der Gleichung
in der Ebene mit der Gleichung 
Bei der Geradenschar
i)
1. Schritt: Parallelität zeigen
![\(\begin{array}[t]{rll}
\pmatrix{0\\-10a\\\frac{2}{a}} \circ \pmatrix{5\\4\\5} &=& 0 \\[5pt]
0\cdot 5 + (-10a)\cdot 4 + \frac{2}{a} \cdot 5 &=& 0 \\[5pt]
-40a + \frac{10}{a} &=& 0 &\quad \scriptsize \mid\;\cdot a \\[5pt]
-40a^2 +10 &=& 0 &\quad \scriptsize \mid\; -10\\[5pt]
-40a^2 &=& -10 &\quad \scriptsize \mid\; :(-40) \\[5pt]
a^2 &=& 0,25 \\[5pt]
a_1 &=& 0,5 \\[5pt]
a_2 &=& -0,5
\end{array}\)](https://mathjax.schullv.de/10e83f25d154ab436a83c57628cdef9fbd48e4fcbd1481ce591def98d7aab071?color=5a5a5a) Da
Da  vorgegeben ist, ist
vorgegeben ist, ist  der einzige Wert, für den die Gerade
der einzige Wert, für den die Gerade  parallel zu
parallel zu  verläuft.
2. Schritt: Gemeinsamen Punkt bestimmen
Der Stützpunkt der Geraden
verläuft.
2. Schritt: Gemeinsamen Punkt bestimmen
Der Stützpunkt der Geraden  hat die Koordinaten
hat die Koordinaten  Einsetzen in die Ebenengleichung liefert:
Einsetzen in die Ebenengleichung liefert:
![\(\begin{array}[t]{rll}
5\cdot 2,5 + 4\cdot 0 + 5\cdot 3,5 -30 &=& 0 \\[5pt]
0 &=& 0
\end{array}\)](https://mathjax.schullv.de/62720faa4a60076cbacd1e73abf1cc7264ead39f81e530f53fb468ccd86df96a?color=5a5a5a) Der Punkt liegt also in der Ebene
Der Punkt liegt also in der Ebene  Insgesamt liegt damit die gesamte Gerade
Insgesamt liegt damit die gesamte Gerade  mit
mit  in der Ebene
in der Ebene 

 3. Schritt: Parallelität zeigen
Wie oben, müssen der Richtungsvektor von
3. Schritt: Parallelität zeigen
Wie oben, müssen der Richtungsvektor von  und der Normalenvektor von
und der Normalenvektor von  senkrecht aufeinander stehen:
senkrecht aufeinander stehen:
![\(\begin{array}[t]{rll}
\pmatrix{0\\-5\\4}\circ \pmatrix{-5\\4\\5} &=& 0\cdot (-5) +(-5) \cdot 4 +4\cdot 5 \\[5pt]
&=& 0
\end{array}\)](https://mathjax.schullv.de/82053afc158fccaf4afd9aef723bdb49b9089d8ac57492d5d25bb6282d788802?color=5a5a5a) Die Gerade
Die Gerade  und
und  verlaufen also parallel zueinander.
4. Schritt: Gemeinsamen Punkt überprüfen
Damit die Gerade
verlaufen also parallel zueinander.
4. Schritt: Gemeinsamen Punkt überprüfen
Damit die Gerade  vollständig in
vollständig in  liegt, muss der Stützpunkt
liegt, muss der Stützpunkt  von
von  in
in  liegen. Einsetzen der Koordinaten in die Ebenengleichung von
liegen. Einsetzen der Koordinaten in die Ebenengleichung von  liefert:
liefert:
![\(\begin{array}[t]{rll}
T](https://mathjax.schullv.de/18cbf8cc70d23c76cba8cb1f970b24e92fe59eae7c8ee9f8729598684d1ccae0?color=5a5a5a) Die Gerade
Die Gerade  liegt also ebenfalls in der Ebene
liegt also ebenfalls in der Ebene 