Analysis 2
Für einen industriellen Produktionsprozess wird ein Behälter verwendet. Im Laufe des Produktionsprozesses enthält der Behälter unterschiedliche Mengen einer Flüssigkeit. Die Füllhöhe der Flüssigkeit im Behälter in Zentimetern wird mit  bezeichnet.
bezeichnet.
1
Die Funktionenschar  mit
mit  beschreibt die Abhängigkeit einer Messgröße von
beschreibt die Abhängigkeit einer Messgröße von 
a)
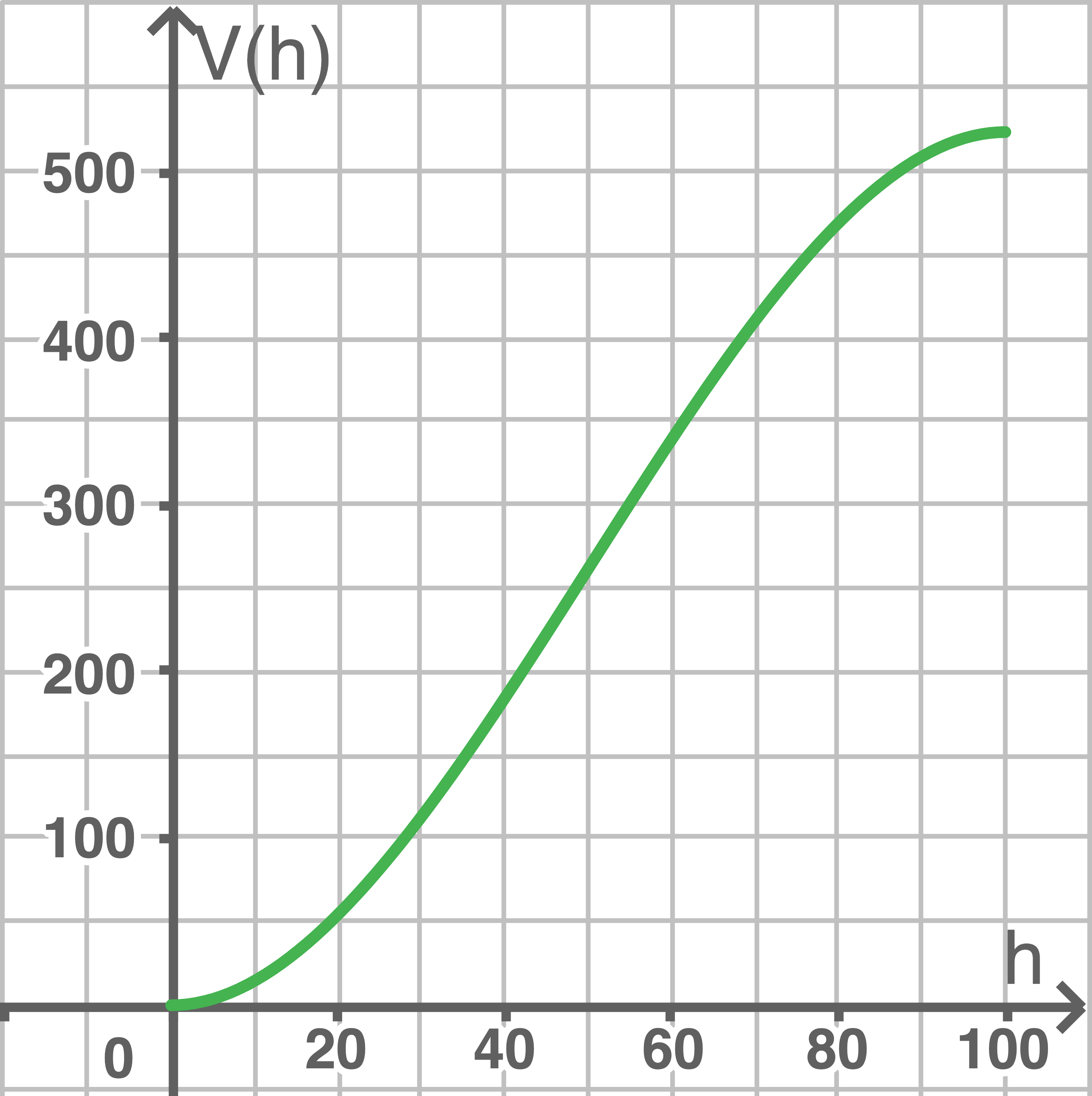
Die Abbildung zeigt die Messwerte der Messreihe 1.
Bestimme die Werte der Parameter und
und  so, dass durch die Funktion
so, dass durch die Funktion  diese Messwerte beschrieben werden.
diese Messwerte beschrieben werden.
Bestimme die Werte der Parameter
| 20 | 55 |
| 40 | 30 |
| 60 | 17 |
| 80 | 9 |
| 100 | 5 |
(4 Punkte)
b)
Verwende nun die Funktion  mit
mit 
Berechne die Füllhöhe bei der die lokale Änderungsrate von
bei der die lokale Änderungsrate von  mit der mittleren Änderungsrate im Intervall
mit der mittleren Änderungsrate im Intervall ![\([0 ; 100]\)](https://mathjax.schullv.de/2be3e1336d070fb296b29cff147371061dbd15e7609752c1e9b61371ff12a878?color=5a5a5a) übereinstimmt.
übereinstimmt.
Berechne die Füllhöhe
(4 Punkte)
c)
Das Ergebnis der Messreihe 2 zeigt das in der Abbildung dargestellte Diagramm, bei dem auf der  -Achse
-Achse  und auf der
und auf der  -Achse
-Achse  abgetragen ist.
abgetragen ist.
Ermittle mithilfe der Steigung der abgebildeten Gerade sowie des Schnittpunktes dieser Gerade mit der Achse die passenden Werte der Parameter
Achse die passenden Werte der Parameter  und
und 
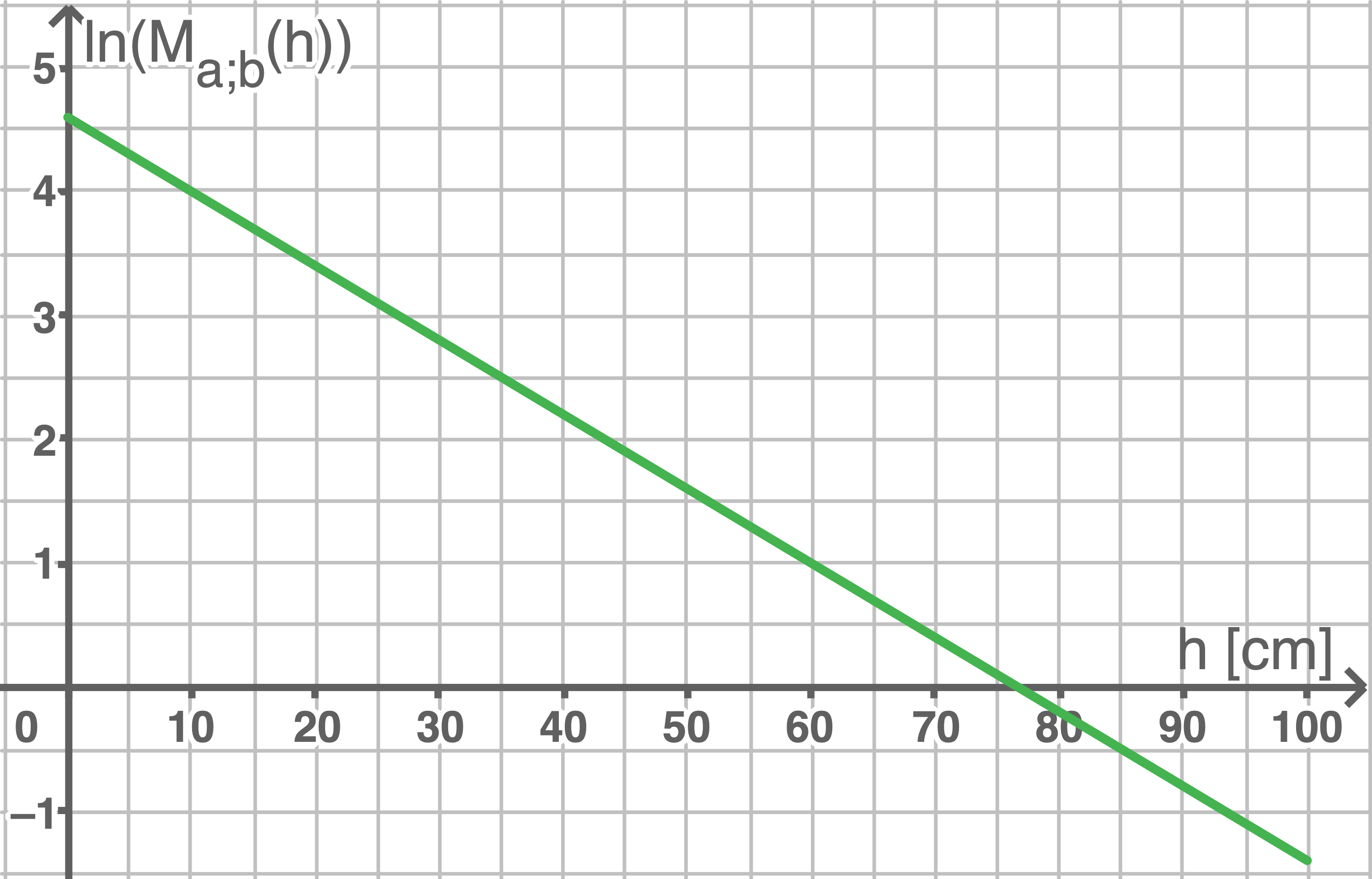
Ermittle mithilfe der Steigung der abgebildeten Gerade sowie des Schnittpunktes dieser Gerade mit der

(5 Punkte)
2
Der betrachtete Behälter ist kugelförmig und hat einen Innendurchmesser von  Das Füllvolumen der Flüssigkeit im Behälter in Litern kann in Abhängigkeit von der Füllhöhe
Das Füllvolumen der Flüssigkeit im Behälter in Litern kann in Abhängigkeit von der Füllhöhe  mit dem Term
mit dem Term  berechnet werden.
berechnet werden.
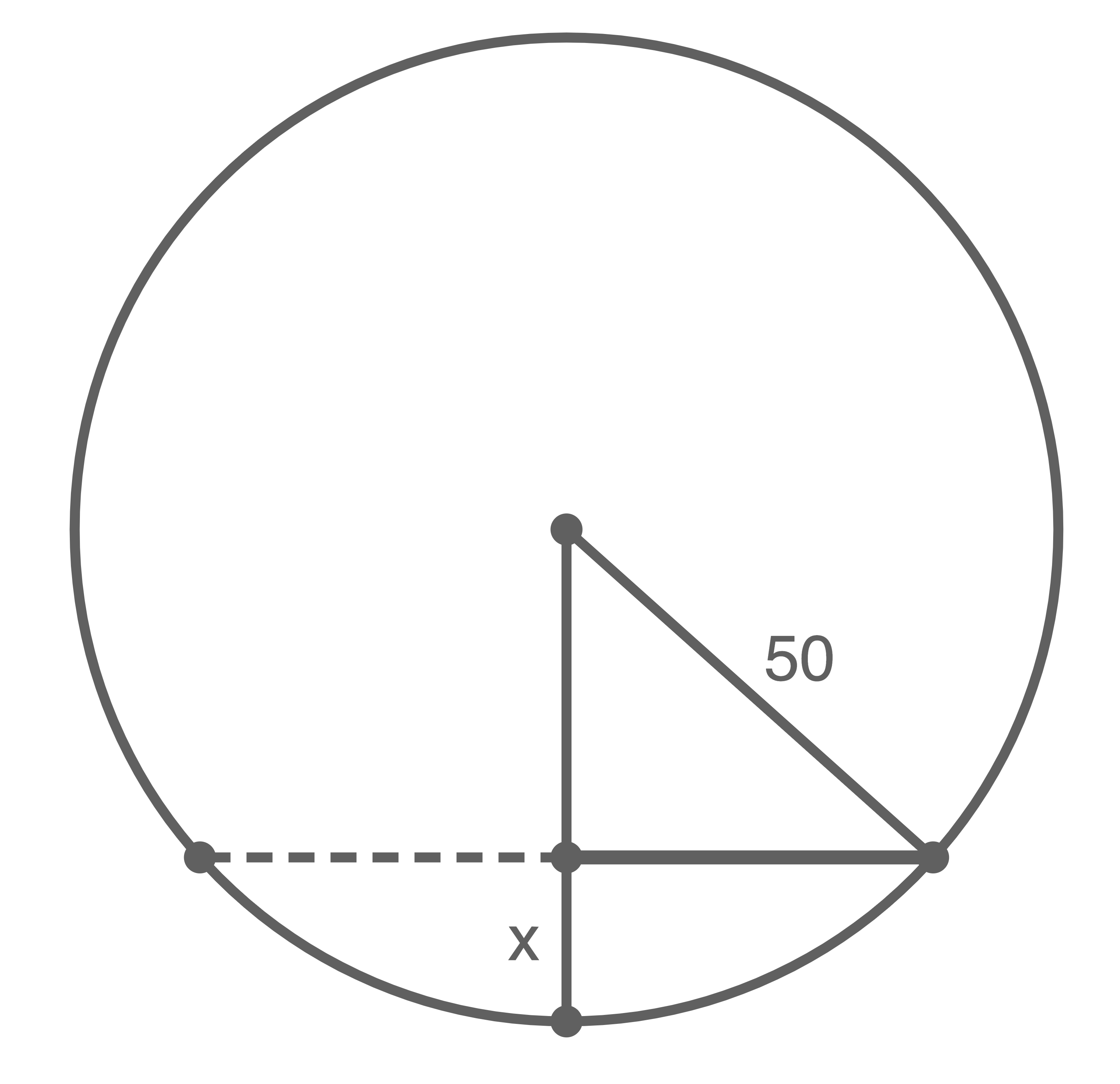
a)
Die Abbildung zeigt einen vertikalen Schnitt durch den Mittelpunkt des Behälters. Gib die Bedeutung des Terms  im Sachzusammenhang an und begründe deine Angabe mithilfe der Abbildung 3. Beschreibe die Bedeutung des Faktors
im Sachzusammenhang an und begründe deine Angabe mithilfe der Abbildung 3. Beschreibe die Bedeutung des Faktors  im Term
im Term  im Sachzusammenhang.
im Sachzusammenhang.

(6 Punkte)
b)
Begründe, dass es im Sachzusammenhang sinnvoll ist, die Definitionsmenge der Funktion  auf das Intervall
auf das Intervall ![\([0;100]\)](https://mathjax.schullv.de/efb20e54f2bc9b17d318e4e3e683023c39357cdb7d63577040fd265ed60c158c?color=5a5a5a) zu beschränken.
zu beschränken.
(2 Punkte)
c)
Bestimme einen Term für  der kein Integral enthält. Skizziere den Graphen dieser Funktion
der kein Integral enthält. Skizziere den Graphen dieser Funktion  im Intervall
im Intervall ![\([0;100].\)](https://mathjax.schullv.de/cfc5275abca8ed6e06b58e0cf1db5e7cedf7a2c0b86863467e10c64d55147193?color=5a5a5a)
(4 Punkte)
d)
Zeige, dass der Wendepunkt des Graphen der Funktion  an der Stelle
an der Stelle  liegt, und berechne das zugehörige Füllvolumen.
liegt, und berechne das zugehörige Füllvolumen.
(4 Punkte)
3
Während des Produktionsprozesses wird dem Behälter kontinuierlich Flüssigkeit zugeführt und wieder entnommen. Die zeitliche Entwicklung des Füllvolumens der Flüssigkeit im Behälter lässt sich mithilfe des Terms  beschreiben. Dabei ist
beschreiben. Dabei ist  die seit Beginn des Produktionsprozesses vergangene Zeit in Minuten und
die seit Beginn des Produktionsprozesses vergangene Zeit in Minuten und  das Füllvolumen in Liter.
das Füllvolumen in Liter.
a)
Begründe, dass das minimale Füllvolumen während des Produktionsprozesses  Liter beträgt.
Liter beträgt.
(2 Punkte)
b)
Berechne denjenigen Zeitpunkt in der ersten halben Stunde nach Beginn des Produktionsprozesses, zu dem das Füllvolumen genau  Liter beträgt. Ermittle die zugehörige Füllhöhe
Liter beträgt. Ermittle die zugehörige Füllhöhe 
(4 Punkte)
c)
Der Mittelwert  einer Funktion
einer Funktion  im Intervall
im Intervall ![\([a;b]\)](https://mathjax.schullv.de/e84e12d6ffce2d83a82ceef8cfb5eb14688a4f4cce00a0d08d5357e2c6858142?color=5a5a5a) ist definiert als
ist definiert als  Untersuche, ob es ein Zeitintervall der Länge zehn Minuten so gibt, dass das mittlere Füllvolumen während dieses Intervalls
Untersuche, ob es ein Zeitintervall der Länge zehn Minuten so gibt, dass das mittlere Füllvolumen während dieses Intervalls  Liter beträgt.
Liter beträgt.
(5 Punkte)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Um die Werte der Parameter  und
und  zu bestimmen, werden die Messwerte in
zu bestimmen, werden die Messwerte in  eingesetzt.
Es ergibt sich
eingesetzt.
Es ergibt sich  und
und  Nach
Nach  aufgelöst ergibt sich:
aufgelöst ergibt sich:  und
und  Aus Gleichsetzen und Auflösen mit dem solve-Befehl des CAS folgt:
Aus Gleichsetzen und Auflösen mit dem solve-Befehl des CAS folgt:
![\(\begin{array}[t]{rll}
\dfrac{55}{\mathrm e^{b \cdot 20}}&=&\dfrac{30}{\mathrm e^{b \cdot 40}} &\quad \scriptsize \mid\;\text{solve} \\[5pt]
b&\approx&-0,03
\end{array}\)](https://mathjax.schullv.de/5fe830ebe360fdf6c8b1b7f3d3a34adf22956d31e049a1c3edee0b6f2029a262?color=5a5a5a) Einsetzen in eine der beiden Gleichungen liefert den Wert für
Einsetzen in eine der beiden Gleichungen liefert den Wert für 
![\(\begin{array}[t]{rll}
55&=& a \cdot \mathrm e^{-0,03 \cdot 20}&\quad \scriptsize \mid\;:\mathrm e^{-0,03 \cdot 20} \\[5pt]
\dfrac{55}{\mathrm e^{-0,03 \cdot 20}}&=& a \\[5pt]
100,21&\approx &a
\end{array}\)](https://mathjax.schullv.de/d1cd0dbf79c5e5f5fb7147453eaa7e31218cbb3cb35a63d9bbda4ee8e30237e7?color=5a5a5a)
b)
Mittlere Änderungsrate im Intervall ![\([0;100]\)](https://mathjax.schullv.de/efb20e54f2bc9b17d318e4e3e683023c39357cdb7d63577040fd265ed60c158c?color=5a5a5a)

 Lokale Änderungsrate bestimmen
Lokale Änderungsrate bestimmen

 Die Füllhöhe
Die Füllhöhe  bei der die lokale Änderungsrate von
bei der die lokale Änderungsrate von  mit der mittleren Änderungsrate übereinstimmt, ergibt sich durch Gleichsetzen:
mit der mittleren Änderungsrate übereinstimmt, ergibt sich durch Gleichsetzen:
![\(\begin{array}[t]{rll}
M](https://mathjax.schullv.de/7d3bb07a52a54ddd14047965528db681d7612740519d6cc1c46bd91f0b7cf884?color=5a5a5a)
c)
1. Schritt: Geradengleichung aufstellen
Die allgemeine Geradengleichung hat die Form  Die Koordinaten des Schnittpunkts der Geraden mit der
Die Koordinaten des Schnittpunkts der Geraden mit der  -Achse werden aus der Abbildung mit
-Achse werden aus der Abbildung mit  abgelesen. Daraus folgt
abgelesen. Daraus folgt  Weitere Koordinaten eines Punktes auf der Geraden können mit
Weitere Koordinaten eines Punktes auf der Geraden können mit  abgelesen werden. Die Steigung
abgelesen werden. Die Steigung  ergibt sich mit
ergibt sich mit  Die Geradengleichung folgt mit
Die Geradengleichung folgt mit  2. Schritt: Term umformen
Anwendung des ersten Logarithmusgesetzes:
2. Schritt: Term umformen
Anwendung des ersten Logarithmusgesetzes:
![\(\begin{array}[t]{rll}
\ln(M_{a;b}(h))&=& \ln(a \cdot \mathrm e^{b \cdot h}) \\[5pt]
\ln(M_{a;b}(h))&=& \ln(a) + \ln(\mathrm e^{b \cdot h})\\[5pt]
&=&\ln(a)+b \cdot h
\end{array}\)](https://mathjax.schullv.de/ba07f9f22fe717fc424a9db17cb47e26378e99336ce46e672081d4ed965fb67c?color=5a5a5a) 3. Schritt: Parameter
3. Schritt: Parameter  und
und  bestimmen
Der Term hat die Form einer linearen Funktion, deshalb entspricht
bestimmen
Der Term hat die Form einer linearen Funktion, deshalb entspricht  der Steigung der Geraden. Also folgt
der Steigung der Geraden. Also folgt  Außerdem folgt:
Außerdem folgt:
![\(\begin{array}[t]{rll}
\ln(a)&=& 4,6 &\quad \scriptsize \mid\;\mathrm e^{(\;)} \\[5pt]
a&\approx& 99,48
\end{array}\)](https://mathjax.schullv.de/82b0abeae4a27e9c77380e483c8eaa1940e4db9bdf0d6200104fb5abc6093baa?color=5a5a5a)
2
a)
Mit dem Satz des Pythagoras und aus der Skizze folgt:
![\(\begin{array}[t]{rll}
50^2&=& (50-x)^2 +y^2 \\[5pt]
50^2-(50-x)^2&=& y^2
\end{array}\)](https://mathjax.schullv.de/b759e900b8a5a864d7e150a3aaf584685df0fbd0634e7240ddb4b47b8bacdb8e?color=5a5a5a)
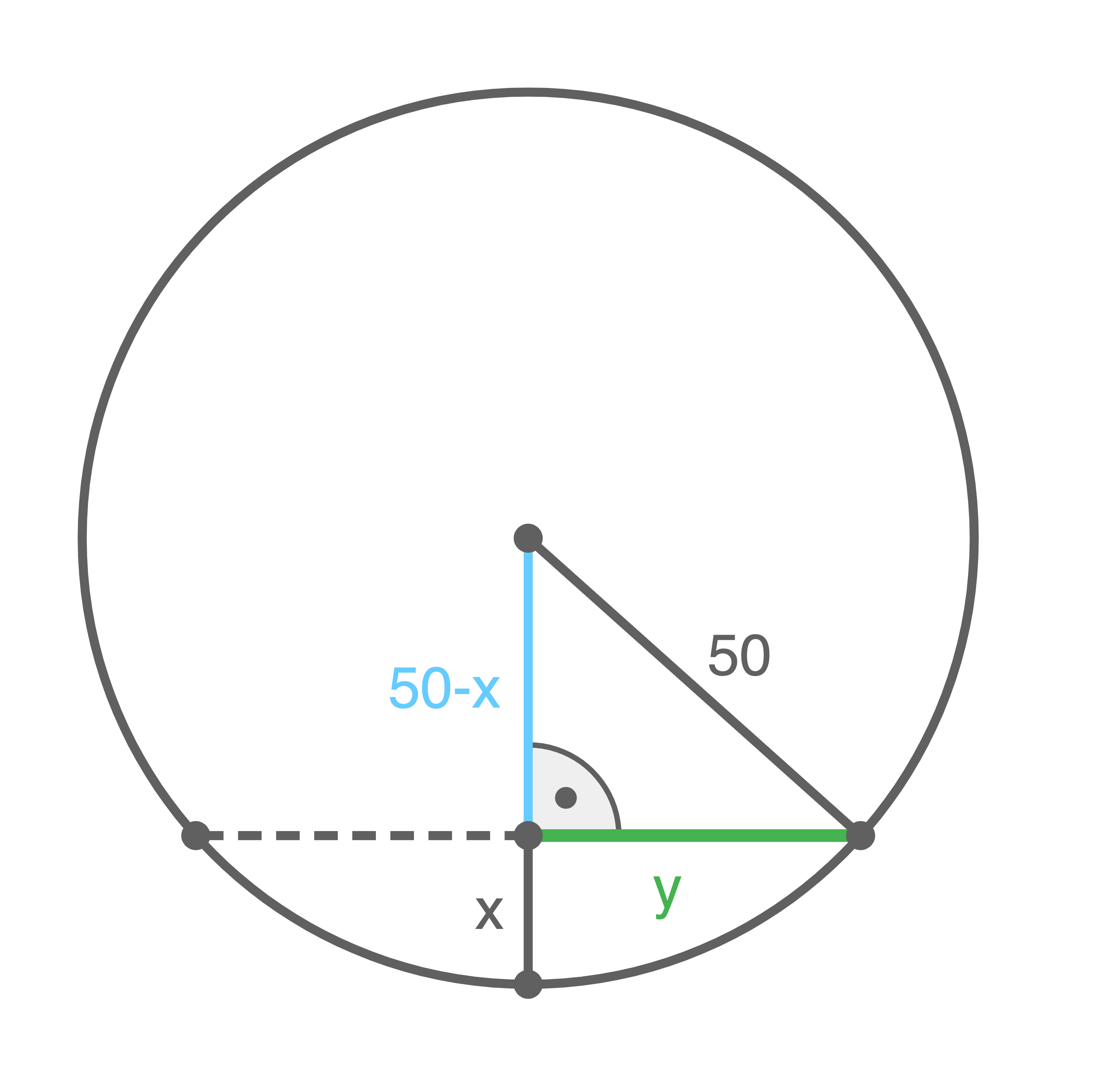
Skizze
b)
Im Sachzusammenhang ist es sinnvoll die Definitionsmenge auf das Intervall ![\([0;100]\)](https://mathjax.schullv.de/efb20e54f2bc9b17d318e4e3e683023c39357cdb7d63577040fd265ed60c158c?color=5a5a5a) zu beschränken, da der Behälter einen Innendurchmesser von
zu beschränken, da der Behälter einen Innendurchmesser von  hat und die Füllhöhe
hat und die Füllhöhe  somit keinen Wert
somit keinen Wert  oder
oder  annehmen kann.
annehmen kann.
c)
d)
Die ersten drei Ableitungen lauten:


 Notwendige Bedingung für Wendestellen anwenden
Notwendige Bedingung für Wendestellen anwenden
![\(\begin{array}[t]{rll}
V](https://mathjax.schullv.de/b30351e4604315c92b044506fb696647ccf6c782200b887063d6c68a626d109a?color=5a5a5a) Hinreichende Bedingung für Wendestellen anwenden
Hinreichende Bedingung für Wendestellen anwenden
 Folglich ist gezeigt, dass sich an der Stelle
Folglich ist gezeigt, dass sich an der Stelle  ein Wendepunkt befindet.
Das zugehörige Füllvolumen ergibt sich mit
ein Wendepunkt befindet.
Das zugehörige Füllvolumen ergibt sich mit ![\(V(50)= \dfrac{250}{\pi} \approx 261,8 \; [\text{l}].\)](https://mathjax.schullv.de/a0e1e34400e7fd2f29594249f51ff23622e5aa135ca693d0d32013ce3589b8be?color=5a5a5a)
3
a)
Es muss  gelten.
gelten.
Der Graph der -Funktion verläuft nämlich periodisch und hat somit unendlich viele Tiefpunkte, die alle
-Funktion verläuft nämlich periodisch und hat somit unendlich viele Tiefpunkte, die alle  als kleinsten Funktionswert annehmen.
Daraus folgt das minimale Füllvolumen mit:
als kleinsten Funktionswert annehmen.
Daraus folgt das minimale Füllvolumen mit:
![\(\begin{array}[t]{rll}
& & 150 \cdot \sin \left(\dfrac{\pi}{12}\cdot t \right)+300 \\[5pt]
&=& 150 \cdot (-1)+300 \\[5pt]
&=&150 \, [\text{l}]
\end{array}\)](https://mathjax.schullv.de/0634534c4d1125e0b528b6ee23b5b30743576df8206c2d5f161145896bac2427?color=5a5a5a)
Der Graph der
b)
Gesucht ist der Zeitpunkt  im Intervall
im Intervall ![\([0;30].\)](https://mathjax.schullv.de/ade4525d56dd628cc4fb46c822c7f7aeb3403a9ad2d38e0ae0ef0c41ddf0fd73?color=5a5a5a) Da der Graph der Sinusfunktion periodisch verläuft, wird ausgehend von
Da der Graph der Sinusfunktion periodisch verläuft, wird ausgehend von  der Zeitpunkt
der Zeitpunkt  eine Periode
eine Periode  weiter in positive
weiter in positive  -Richtung berechnet.
Es gilt:
-Richtung berechnet.
Es gilt:  Daraus folgt:
Daraus folgt:  Nach 18 Minuten beträgt das Füllvolumen in der ersten halben Stunde genau 150 Liter.
Nach 18 Minuten beträgt das Füllvolumen in der ersten halben Stunde genau 150 Liter.
c)
1. Schritt: Stammfunktion ermitteln

 2. Schritt: Zeitintervall bestimmen
Gesucht ist das Intervall
2. Schritt: Zeitintervall bestimmen
Gesucht ist das Intervall ![\([t;t+10]\)](https://mathjax.schullv.de/0ee4e7d899239f05c80f8b8f5785cc3cd0c4eb30e5fc427d16584acf84542344?color=5a5a5a) in dem
in dem  ist. Einsetzen in
ist. Einsetzen in  ergibt:
Das
ergibt:
Das  für das
für das  gilt, ergibt sich aus der Graphischen Lösung mithilfe des CAS. Ermittelt wird eine mögliche
gilt, ergibt sich aus der Graphischen Lösung mithilfe des CAS. Ermittelt wird eine mögliche  -Koordinate des Schnittpunkts des Terms mit der Geraden
-Koordinate des Schnittpunkts des Terms mit der Geraden  Diese ergibt sich mit
Diese ergibt sich mit  Somit folgt ein mögliches Intervall mit
Somit folgt ein mögliches Intervall mit ![\([2,693; 12,693].\)](https://mathjax.schullv.de/bcdfb58a774da271d2d289b638c3d3716eced471d08ba255b7de5aa74b6d4207?color=5a5a5a)