A3
a)
Gegeben ist eine in  definierte Funktion
definierte Funktion  mit
mit  wobei
wobei  eine positive reelle Zahl ist. Abbildung 1 zeigt den Graphen von
eine positive reelle Zahl ist. Abbildung 1 zeigt den Graphen von 
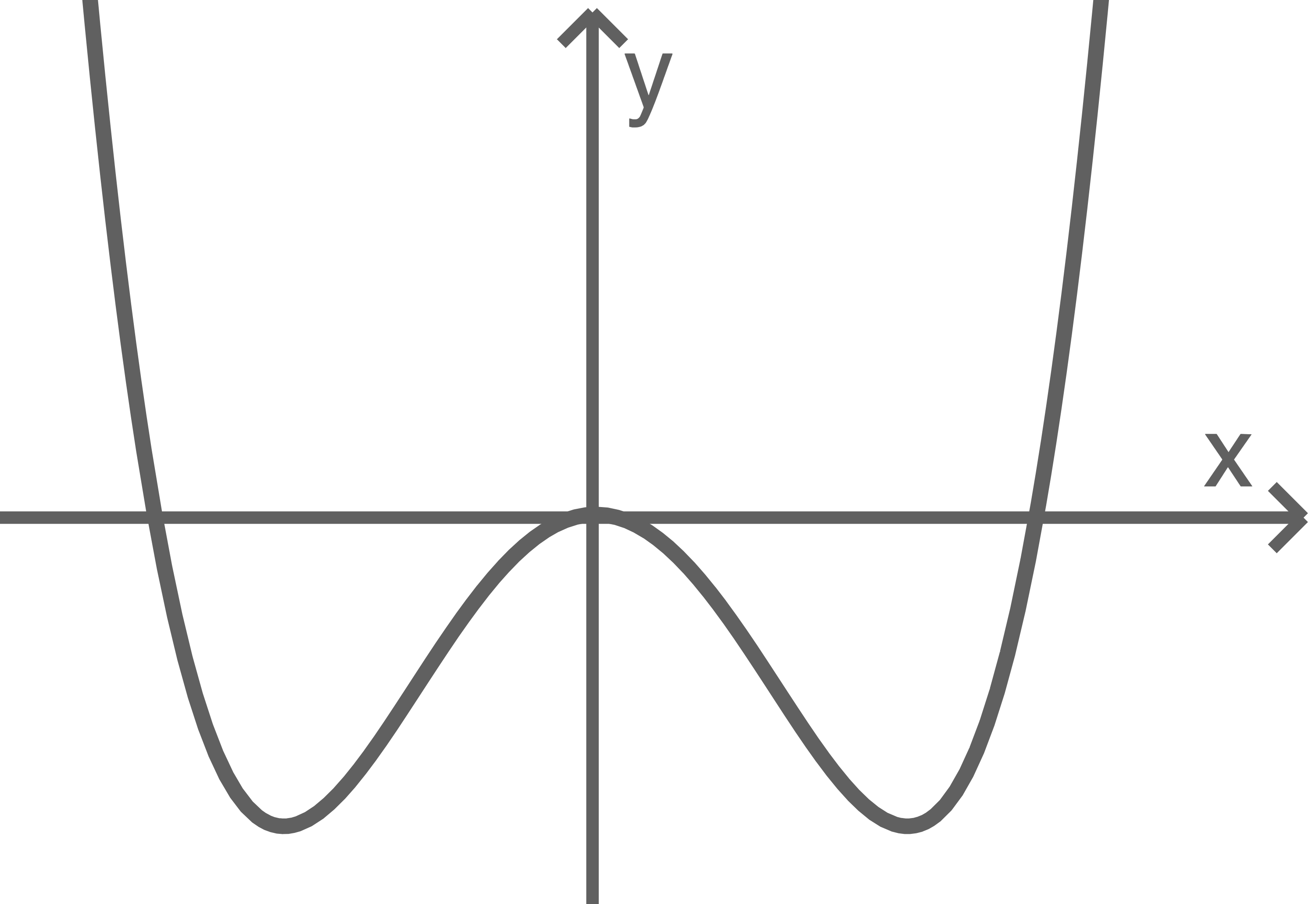

Abbildung 1
(1)
Zeige, dass  eine Gleichung der ersten Ableitungsfunktion von
eine Gleichung der ersten Ableitungsfunktion von  ist.
ist.
(2)
Die beiden Tiefpunkte des Graphen von  haben jeweils die
haben jeweils die  -Koordinate
-Koordinate  .
.
Ermittle den Wert von
Ermittle den Wert von
(1 + 4 Punkte)
b)
Die Funktion  ist gegeben durch
ist gegeben durch 
 Die Funktion
Die Funktion  ist eine Stammfunktion zur Funktion
ist eine Stammfunktion zur Funktion  Der Graph von
Der Graph von  ist in Abbildung 2 dargestellt.
ist in Abbildung 2 dargestellt.
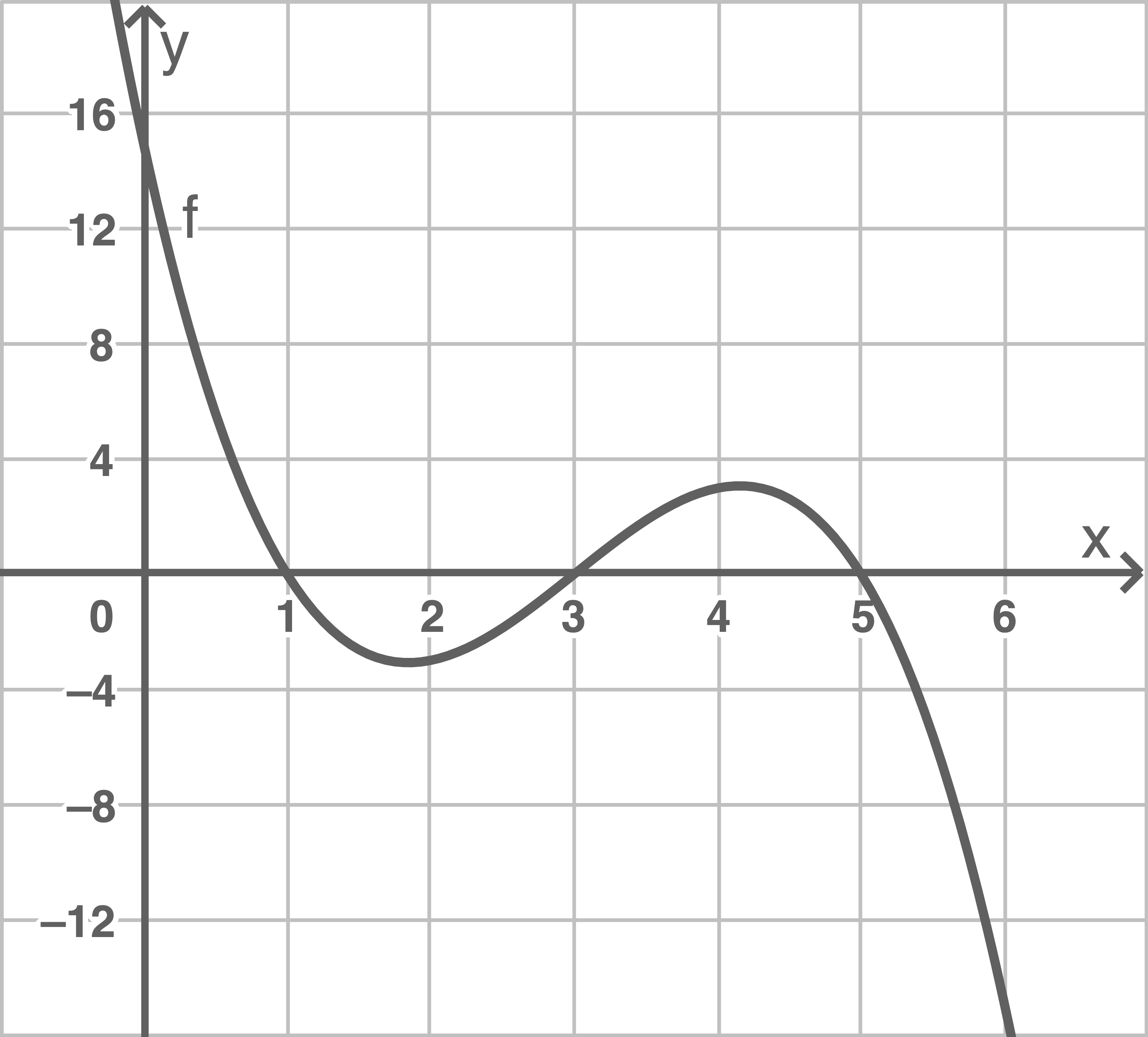

Abbildung 2
(1)
Interpretiere die Aussage  in Bezug auf den Graphen von
in Bezug auf den Graphen von 
(2)
Berechne 
(2 + 3 Punkte)
c)
Gegeben ist die Funktion  mit
mit  mit
mit 
Der Graph von ist in Abbildung 3 dargestellt.
ist in Abbildung 3 dargestellt.
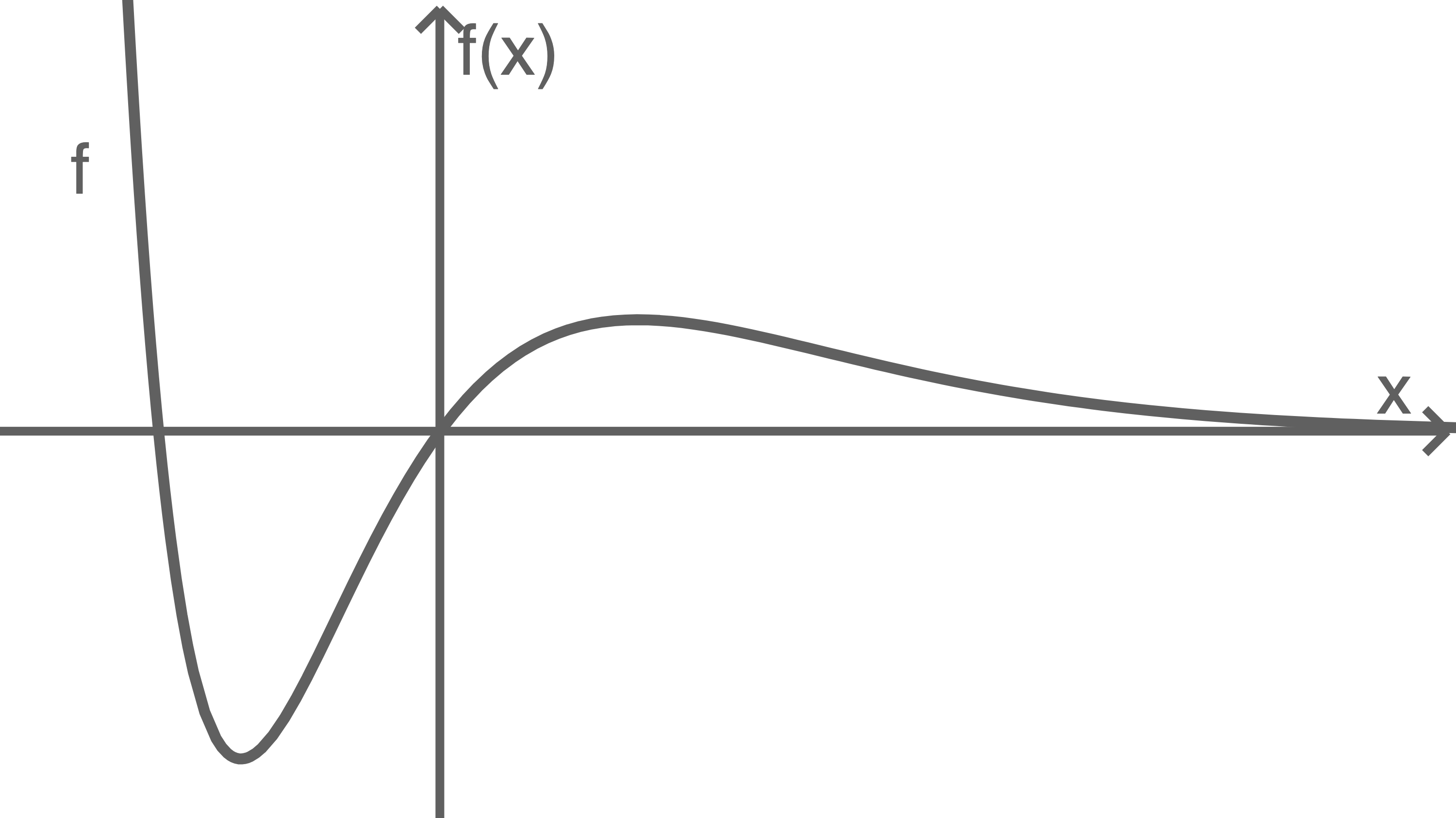
Der Graph von

Abbildung 3
(1)
Die Funktion  besitzt genau zwei Extremstellen.
besitzt genau zwei Extremstellen.
Ermittle die beiden Extremstellen von
Hinweis: Ein Nachweis der hinreichenden Bedingung ist nicht erforderlich.
Ermittle die beiden Extremstellen von
Hinweis: Ein Nachweis der hinreichenden Bedingung ist nicht erforderlich.
(2)
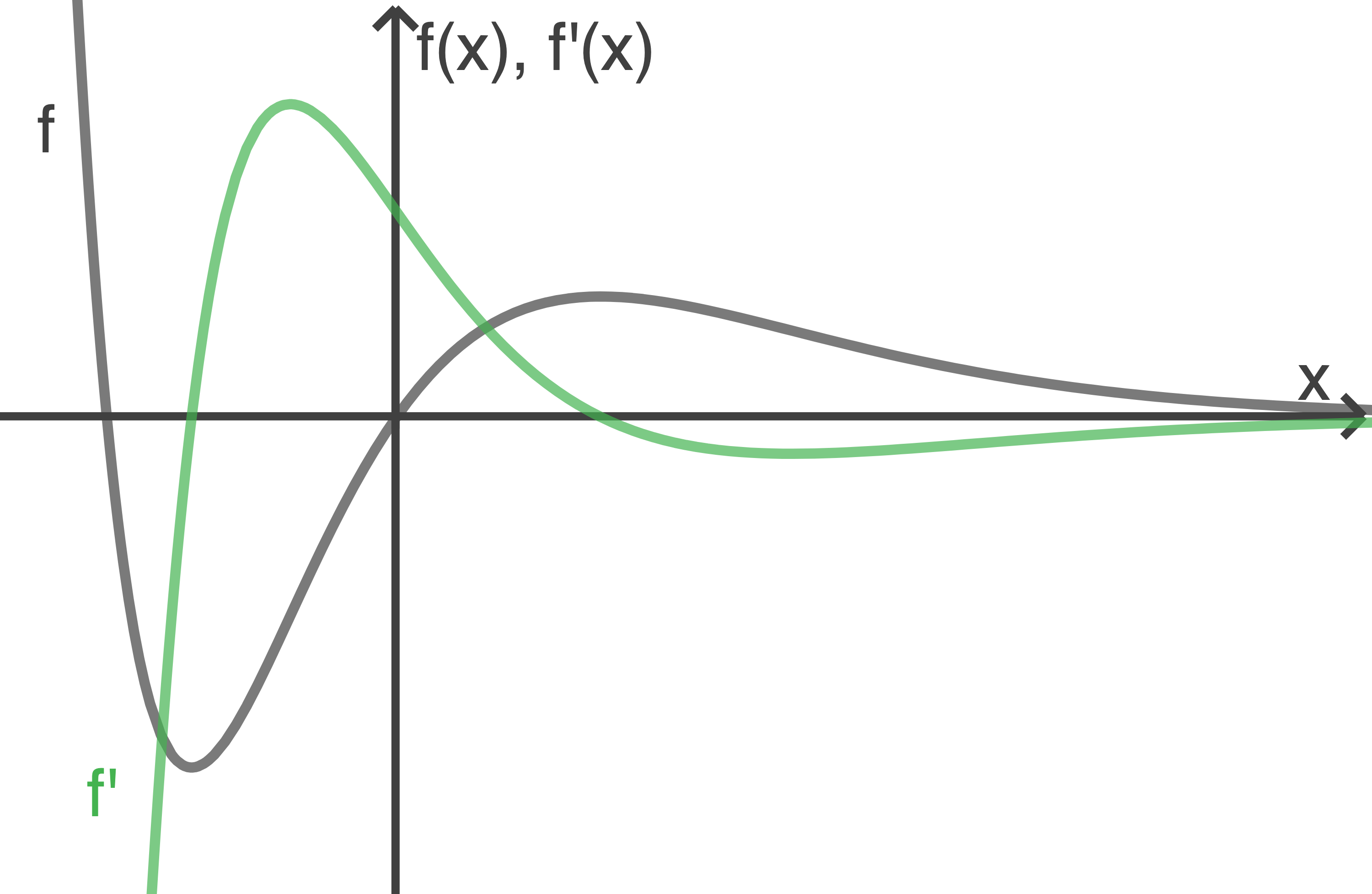
Skizziere in Abbildung 3 den Graphen der ersten Ableitungsfunktion von 
Hinweis: Die Größe der -Werte kann dabei unberücksichtigt bleiben.
-Werte kann dabei unberücksichtigt bleiben.
Hinweis: Die Größe der
(3 + 2 Punkte)
d)
Für jedes  ist durch die Gleichung
ist durch die Gleichung

eine Funktion gegeben.
In Abbildung 4 ist der Graph der Funktion
gegeben.
In Abbildung 4 ist der Graph der Funktion  für
für  abgebildet.
abgebildet.
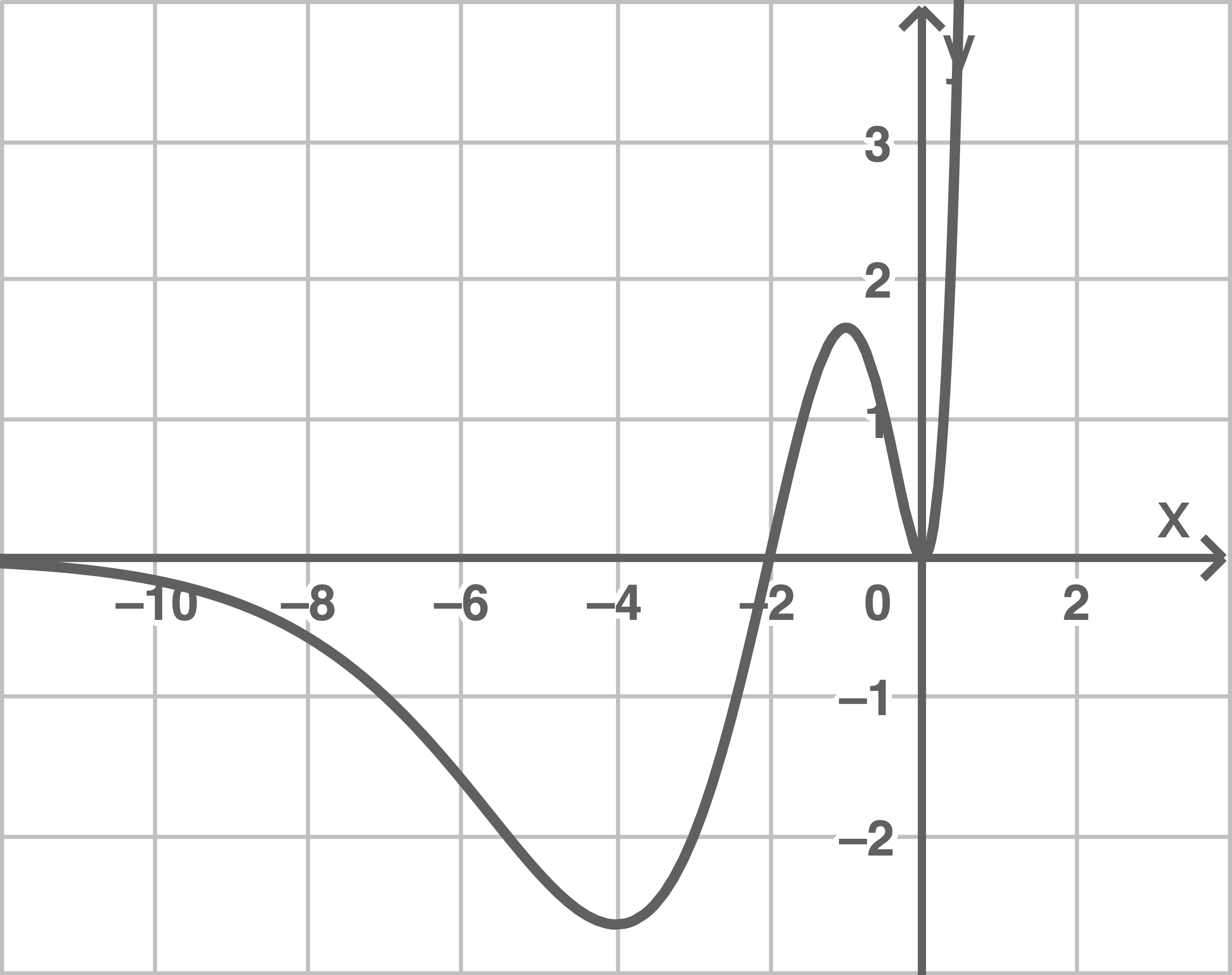
eine Funktion

Abbildung 4
(1)
Es gibt genau einen Wert von  sodass die Funktion
sodass die Funktion  nur eine Nullstelle besitzt.
nur eine Nullstelle besitzt.
Ermittle diesen Wert von
Ermittle diesen Wert von
(2)
Ermittle, für welche Werte von  der Punkt
der Punkt  auf dem Graphen der Funktion
auf dem Graphen der Funktion  liegt.
liegt.
(2 + 3 Punkte)
e)
Betrachtet werden die Ebene  und für
und für  die Gerade
die Gerade  mit
mit 
(1)
Bestimme, denjenigen Wert von  für den die Gerade
für den die Gerade  senkrecht zu
senkrecht zu  steht.
steht.
(2)
Untersuche, ob es einen Wert von  gibt, für den die Gerade
gibt, für den die Gerade  in
in  liegt.
liegt.
(2 + 3 Punkte)
f)
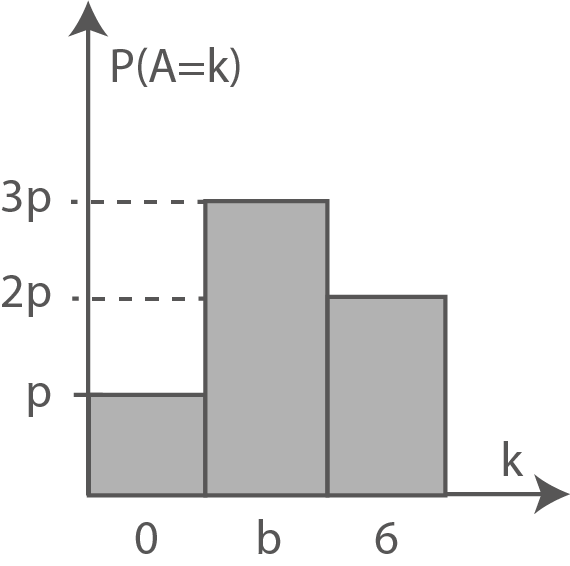
Bei einem Gewinnspiel beträgt der Einsatz für die Teilnahme 3 Euro. Die Auszahlung in Euro wird durch die Zufallsgröße  beschrieben. Abbildung 5 zeigt die Wahrscheinlichkeitsverteilung von
beschrieben. Abbildung 5 zeigt die Wahrscheinlichkeitsverteilung von 
(1)
Zeige, dass  den Wert
den Wert  hat.
hat.
(2)
Bei wiederholter Durchführung des Spiels ist zu erwarten, dass sich auf lange Sicht Einsätze und Auszahlungen ausgleichen.
Berechne den Wert von
Berechne den Wert von
(3)
Beschreibe, wie das Gewinnspiel unter Verwendung eines Behälters sowie roter, grüner und blauer Kugel durchgeführt werden könnte.
(1 + 2 + 2 Punkte)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
(1)
(2)
Mit der notwendigen Bedingung für Extremstellen folgt:
![\(\begin{array}[t]{rlll}
f](https://mathjax.schullv.de/1af6f04ded1a895f0219b488904d2d8146ce8dadc2eb0fa1c263dfaa84e59cb4?color=5a5a5a) Mit dem Satz vom Nullprodukt folgt
Mit dem Satz vom Nullprodukt folgt  und
und 
![\(\begin{array}[t]{rll}
2x^2-k &= & 0 \quad \scriptsize \mid +k \mid :2\\[5pt]
x^2 &= & \frac{k}{2} \quad \scriptsize \mid \sqrt{\,\,} \\[5pt]
x_{2,3} &= & \pm \sqrt{\frac{k}{2}}& \quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/f73efd0da6fd7c0403641769301c9c7cf4fca4207c89d54ad2aeb05d13f9f639?color=5a5a5a) Auf die hinreichende Bedingung kann verzichtet werden, weil aus der Aufgabe bekannt ist, dass es genau zwei Tiefpunkte gibt. Da nicht zwei Tiefpunkte aufeinander folgen können, muss bei
Auf die hinreichende Bedingung kann verzichtet werden, weil aus der Aufgabe bekannt ist, dass es genau zwei Tiefpunkte gibt. Da nicht zwei Tiefpunkte aufeinander folgen können, muss bei  ein Hochpunkt liegen und zwei Tiefpunkte bei
ein Hochpunkt liegen und zwei Tiefpunkte bei  liegen.
Es soll gelten
liegen.
Es soll gelten  und
und 
Für ergibt sich ebenfalls
ergibt sich ebenfalls  Da
Da  eine positive reelle Zahl sein soll, folgt
eine positive reelle Zahl sein soll, folgt 
Für
b)
(1)
Der Flächeninhalt der Fläche, die der Graph von  und die
und die  Achse im Intervall
Achse im Intervall ![\([1;3]\)](https://mathjax.schullv.de/4c871f3c45250ceb60647b58544ce3c3596fbc24341f187d6b6947c96521272c?color=5a5a5a) einschließt, ist genauso groß wie der Flächeninhalt der Fläche, die der Graph von
einschließt, ist genauso groß wie der Flächeninhalt der Fläche, die der Graph von  und die
und die  Achse im Intervall
Achse im Intervall ![\([3;5]\)](https://mathjax.schullv.de/9b74aa626c8d7e31a85e07aab7436e3c3c0ef3498047b88831b04d1ff79420d3?color=5a5a5a) einschließt.
einschließt.
(2)
c)
(1)
Mit der Produktregel folgt:


 Mit der notwendigen Bedingung für Extremstellen folgt:
Mit der notwendigen Bedingung für Extremstellen folgt:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/55d5f5177523770ba532807dd93c9276dfa26c35512511fa4c4325c04b1e7987?color=5a5a5a) Da
Da  ist, muss
ist, muss  gelten. Damit folgt:
gelten. Damit folgt:
![\(\begin{array}[t]{rll}
2-x^2&=& 0 \quad \scriptsize \mid \,+x^2\\[5pt]
2&=& x^2 \quad \scriptsize \\[5pt]
x^2&=& 2 \quad \scriptsize \mid \,\sqrt{\, \,}\\[5pt]
x_{1/2} &=& \pm \sqrt{2} & \quad \scriptsize\\[5pt]
\end{array}\)](https://mathjax.schullv.de/37d3f0fba8a35f2c3c7023273be86ebb24c40d8ac4917c4fe0944beeff9854db?color=5a5a5a) Die Extremstellen sind:
Die Extremstellen sind:  und
und 
(2)
d)
(1)
(2)
e)
(1)
(2)
f)
(1)
(2)
(3)
In den Behälter werden eine rote, drei grüne und zwei blaue Kugeln gelegt. Die Spielerin/der Spieler entnimmt dem Behälter zufällig eine Kugel. Ist die entnommene Kugel rot, erfolgt keine Auszahlung, ist sie grün, werden 2 Euro ausgezahlt und ist sie blau, werden 6 Euro ausgezahlt.