Aufgabe 4

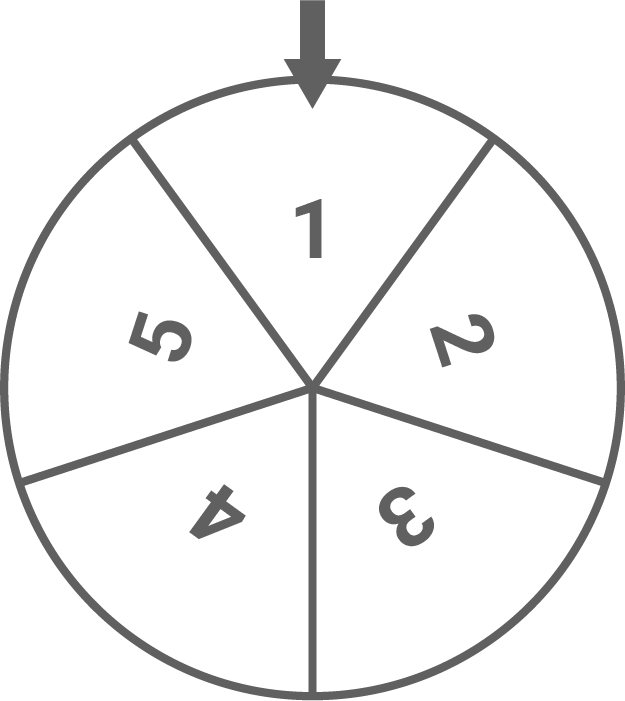
Mit einem Glücksrad mit fünf gleich großen Sektoren (siehe Abbildung 1), einem Spielplan und einer Figur (siehe Abbildung 2) wird folgendes Spiel gespielt:

Abbildung 1: Glücksrad

Abbildung 2: Spielplan mit Figur

Zu Beginn entscheidet der Spieler, ob er sein Spiel auf dem Feld $2,$ $3$ oder $4$ beginnt. Er stellt die Figur auf dem Spielplan auf das Feld mit der entsprechenden Zahl. Anschließend wird das Glücksrad gedreht. Die Figur bewegt sich dann nach den folgenden Regeln:

Zeigt der Pfeil am Glücksrad auf die Zahl des Feldes, auf dem sich die Figur befindet, so bleibt die Figur auf diesem Feld.
Zeigt der Pfeil auf eine Zahl, die größer als die Zahl des Feldes ist, auf dem sich die Figur befindet, so wandert die Figur ein Feld nach rechts.
Zeigt der Pfeil auf eine Zahl, die kleiner als die Zahl des Feldes ist, auf dem sich die Figur befindet, so wandert die Figur ein Feld nach links.

Erreicht die Figur das Feld $1,$ so hat der Spieler das Spiel verloren und das Spiel ist beendet.

Erreicht die Figur das Feld $5,$ so hat der Spieler das Spiel gewonnen und das Spiel ist beendet.

Das Spiel kann als stochastischer Prozess mit den Zuständen $Z_{1},$ $Z_{2},$ $Z_{3},$ $Z_{4}$ und $Z_{5}$ modelliert werden. Zustand $Z_{1}$ bedeutet, dass sich die Figur auf dem Feld $1$ befindet, Zustand $Z_{2}$ bedeutet, dass sich die Figur auf dem Feld $2$ befindet usw.

Der Spielverlauf kann durch die Matrix $M$ modelliert werden:

$Z_1$

$Z_2$

$Z_3$

$Z_4$

$Z_5$

von /
nach

$M=\begin{pmatrix}1&\frac{1}{5}&0&0&0\\[2pt]0&\frac{1}{5}&\frac{2}{5}&0&0\\[2pt]0&\frac{3}{5}&\frac{1}{5}&\frac{3}{5}&0\\[2pt]0&0&\frac{2}{5}&\frac{1}{5}&0\\[2pt]0&0&0&\frac{1}{5}&1\end{pmatrix}$

$\begin{array}[t]{r} \\ Z_1\\[5pt] Z_2\\[5pt] Z_3\\[5pt] Z_4\\[5pt] Z_5\\ \end{array}$

(1)

Erkläre aus dem Sachzusammenhang, wie sich die Übergangswahrscheinlichkeiten in der zweiten Spalte der Matrix $M$ ergeben.

(2)

Erstelle ein zur Matrix $M$ passendes Übergangsdiagramm.

(3)

Wenn der Spieler sein Spiel auf dem Feld $3$ beginnt, so ist es für ihn gleich wahrscheinlich, das Spiel zu gewinnen oder zu verlieren.
Erkläre anhand der Übergangswahrscheinlichkeiten ohne weitere Berechnung diese Tatsache.

(4 + 4 + 3 Punkte)

(1)

Bestimme die Wahrscheinlichkeit dafür, dass ein Spieler, der sein Spiel auf dem Feld $3$ beginnt, nach höchstens zehn Drehungen des Glücksrades das Spiel gewinnt.

(2)

Ermittle die Wahrscheinlichkeit dafür, dass das Spiel nach höchstens sieben Drehungen beendet ist, wenn der Spieler auf dem Feld $2$ beginnt.

(3)

Ermittle die Wahrscheinlichkeit dafür, dass das Spiel nach genau sieben Drehungen beendet ist, wenn der Spieler auf dem Feld $2$ beginnt.

(4)

Ein Spieler beginnt das Spiel auf einem bestimmten Startfeld. Der Spielbeginn wird durch den Vektor $\overrightarrow{s}$ beschrieben.

Für ein geeignetes $n \in \mathbb{N}$ gilt dann: $M^n \cdot \overrightarrow{s}= \pmatrix{\frac{48}{625}\\\frac{108}{625}\\\frac{156}{625}\\\frac{109}{625}\\\frac{204}{625}}=\pmatrix{0,0768\\0,1728\\0,2496\\0,1744\\0,3264}=\overrightarrow{v}.$

Untersuche, welches Startfeld und welcher Wert von $n$ zum Vektor $\overrightarrow{v}$ führen.

(4 + 4 + 5 + 5 Punkte)

Im Folgenden soll untersucht werden, mit welchen Wahrscheinlichkeiten $g_2$ , $g_3$ bzw. $g_4$ der Spieler das Spiel ausgehend von den Feldern $2,$ $3$ bzw. $4$ gewinnt. Diese Wahrscheinlichkeiten können mit dem folgenden linearen Gleichungssystem ermittelt werden:

$\begin{vmatrix}\text{I}&g_2&=&\dfrac{1}{5}\cdot g_2+\dfrac{3}{5}\cdot g_3\\\text{II}&g_3&=&\dfrac{2}{5}\cdot g_2+\dfrac{1}{5}\cdot g_3+\dfrac{2}{5}\cdot g_4\\\text{III}&g_4&=&\dfrac{3}{5}\cdot g_3+\dfrac{1}{5}\cdot g_4+\dfrac{1}{5}\end{vmatrix}$

(1)

Leite mithilfe der Übergangswahrscheinlichkeiten die Gleichung $\text{I}$ des linearen Gleichungssystems her.

(2)

Ermittle die Wahrscheinlichkeiten $g_2$ , $g_3$ und $g_4$ .

(3)

$v_2,$ $v_3$ bzw. $v_4$ sind die Wahrscheinlichkeiten, dass der Spieler ausgehend von den Feldern $2,$ $3$ bzw. $4$ verliert.

Stelle ein entsprechendes lineares Gleichungssystem für die Wahrscheinlichkeiten $v_2$ , $v_3$ und $v_4$ auf.

(4 + 4 + 3 Punkte)

(1)

Befindet sich die Figur auf dem Feld 2 (Zustand $Z_2$ ), ...

so wandert die Figur zum Feld 1 (Zustand $Z_1$ ), wenn bei der nächsten Drehung die Zahl 1 auftritt, was mit einer Wahrscheinlichkeit von $p=\dfrac{1}{5}$ passiert.
so bleibt die Figur auf dem Feld 2 (Zustand $Z_2$ ), wenn bei der nächsten Drehung die Zahl 2 auftritt, was mit einer Wahrscheinlichkeit von $p=\dfrac{1}{5}$ geschieht.
so wandert die Figur zum Feld 3 (Zustand $Z_3$ ), wenn bei der nächsten Drehung eine der Zahlen 3,4 oder 5 auftritt, was mit einer Wahrscheinlichkeit von $p=\dfrac{3}{5}$ passiert.

Es gibt keine Möglichkeit die Felder 4 und 5 (Zustände $Z_4$ und $Z_5$ ) von Feld 2 aus direkt zu erreichen.

(2)

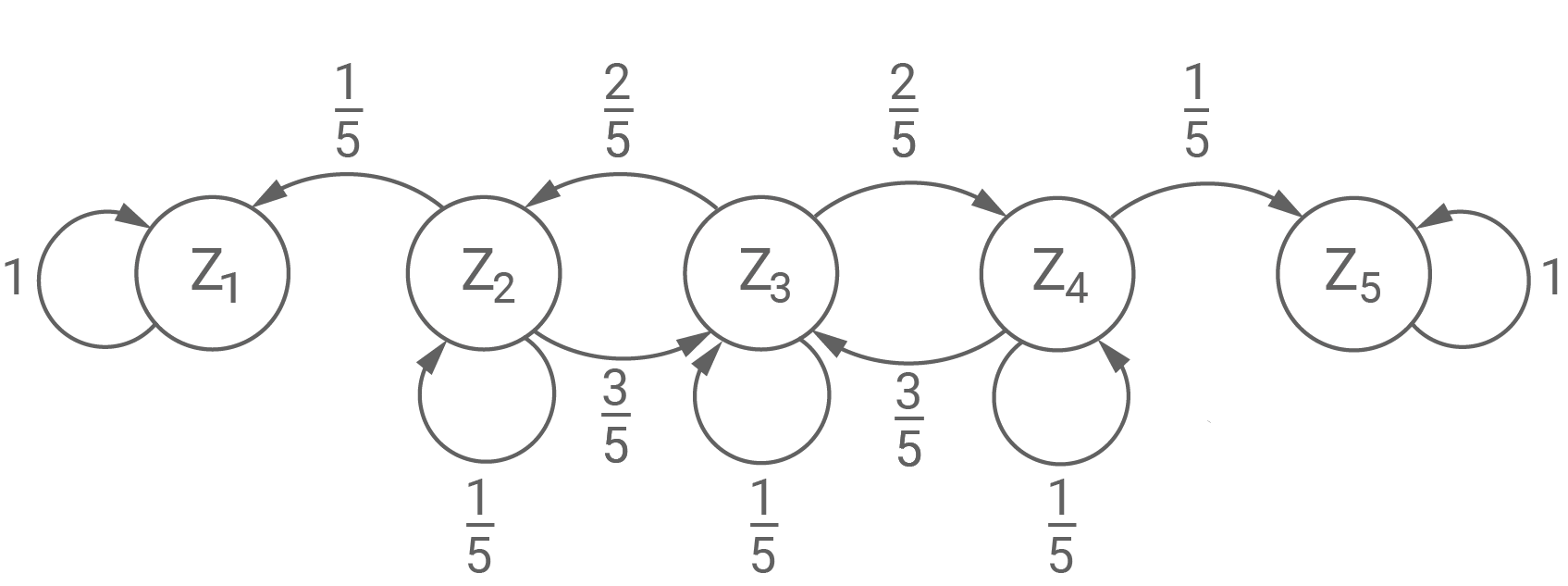
(3)

Von der Mitte des Spielfeldes aus gesehen stimmen die Wahrscheinlichkeiten, mit denen die Spielfigur nach links wandert, mit den Wahrscheinlichkeiten überein, mit denen die Spielfigur nach rechts wandert. Auch die Wahrscheinlichkeiten, von den Spielfeldern 2 und 4 wieder zur Mitte des Spielfeldes zu gelangen, stimmen überein.
Daher ist es vom Feld 3 aus gleich wahrscheinlich, die Felder 1 und 5 zu erreichen und damit zu verlieren beziehungsweise zu gewinnen.

(1)

Rechenweg anzeigen

$M^{10} \cdot \pmatrix{0\\0\\1\\0\\0}\approx \pmatrix{... \\ ...\\... \\... \\ 0,3267}$

Die Wahrscheinlichkeit dafür, dass ein Spieler, der sein Spiel auf dem Feld 3 beginnt, nach höchstens zehn Drehungen des Glücksrades das Spiel gewinnt, beträgt ungefähr $0,3267= 32,67\,\%.$

(2)

Rechenweg anzeigen

$M^{7} \cdot \pmatrix{0\\0\\1\\0\\0} \approx \pmatrix{ 0,4143\\... \\ ...\\... \\ 0,1643}$

Die Wahrscheinlichkeit dafür, dass das Spiel nach höchstens 7 Drehungen beendet ist, wenn der Spieler auf dem Feld 2 beginnt, beträgt ungefähr $0,4143 + 0,1643 = 0,5786 = 57,86\,\%.$

(3)

Rechenweg anzeigen

$M^{6} \cdot \pmatrix{0\\0\\1\\0\\0} \approx \pmatrix{ 0,3882\\ ...\\ ...\\... \\ 0,1382}$

Die Wahrscheinlichkeit dafür, dass das Spiel nach genau sieben Drehungen beendet ist, wenn der Spieler auf dem Feld 2 beginnt, beträgt ungefähr $0,5786-0,3882-0,1382 =5,22\,\%.$

(4)

Da im Vektor $\overrightarrow{v}$ die Wahrscheinlichkeit für den Zusatand $Z_5$ größer als die Wahrscheinlichkeit für den Zustand $Z_1$ , hat der Spieler das Spiel vermutlich auf Feld 4 begonnen, d.h. es gilt vermutlich $\overrightarrow{s}= \pmatrix{0\\0\\1\\0\\0}$ .

Der Vergleich des Nenners $625 (=5^4)$ , der in den Wahrscheinlichkeiten im Vektor $\overrightarrow{v}$ auftritt, mit dem Nenner 5, der in den Übergangswahrscheinlichkeiten in der Matrix $M$ auftritt, lässt vermuten, dass $n=4$ gilt.

$M^4 \cdot \pmatrix{0\\0\\1\\0\\0} = \pmatrix {\frac{48}{625} \\ \frac{108}{625}\\ \frac{156}{625}\\ \frac{109}{625}\\ \frac{204}{625} } = \pmatrix {0,0768\\0,1728\\0,2496\\0,1744\\0,3264}$ bestätigt diese Vermutungen.

(1)

Um vom Feld 2 aus zu gewinnen, gibt es zwei Möglichkeiten:

Man bleibt nach der ersten Umdrehung des Glücksrades zunächst auf dem Feld 2, dies geschieht mit der Wahrscheinlichkeit $\dfrac{1}{5}$ . Da man von dort mit der Wahrscheinlichkeit $g_2$ gewinnt, beträgt die Wahrscheinlichkeit, mit dieser Möglichkeit zu gewinnen, $\dfrac{1}{5} \cdot g_2.$
Man gelangt bei der nächsten Umdrehung des Glücksrades zunächst auf das Feld 3, dies geschieht mit der Wahrscheinlichkeit $\dfrac{3}{5}$ . Da man von dort mit der Wahrscheinlichkeit $g_3$ gewinnt, beträgt die Wahrscheinlichkeit, mit dieser Möglichkeit zu gewinnen, $\dfrac{3}{5} g_3$

Zusammen gilt die Gleichung $\text{I}: \dfrac{1}{5} g_2 + \dfrac{3}{5} \cdot g_3$

(2)

Mit dem Taschenrechner ergibt sich:

$\begin{array}{lrll} \text{I}\quad& g_2&=& \dfrac{1}{5} g_2 + \dfrac{3}{5} g_3 &\quad \scriptsize\\ \text{II}\quad& g_3&=& \dfrac{2}{5}g_2 + \dfrac{1}{5}g_3 + \dfrac{2}{5} g_4 &\quad \scriptsize\\ \text{III}\quad& g_4&=& \dfrac{3}{5}g_3 + \dfrac{1}{5}g_4 + \dfrac{1}{5} &\quad \\ \end{array}$

$\begin{array}[t]{rll} g_2&=& \dfrac{3}{8} =0,375 &\quad \scriptsize \; \\[5pt] g_3&=& \dfrac{1}{2} =0,5 &\quad \scriptsize \; \\[5pt] g_4&=& \dfrac{5}{8} =0,625 \end{array}$

(3)

$\begin{array}{lrll} \text{I}\quad&v_2&=& \dfrac{1}{5} +\dfrac{1}{5} \cdot v_2 + \dfrac{3}{5}v_3 &\quad \scriptsize\\ \text{II}\quad&v_3&=& \dfrac{2}{5} \cdot v_2 + \dfrac{1}{5} v_3 + \dfrac{2}{5} v_4 &\quad \scriptsize\\ \text{III}\quad&v_4&=& \dfrac{3}{5} v_3 + \dfrac{1}{5} v_4 &\quad \\ \end{array}$