Aufgabe 1

Die Funktion $f$ ist gegeben durch die Gleichung

$f(x)=\left(x^3-5\right) \cdot \mathrm e ^x, x \in \mathbb{R} .$

Der Graph von $f$ ist in Abbildung 1 dargestellt.

Abbildung 1

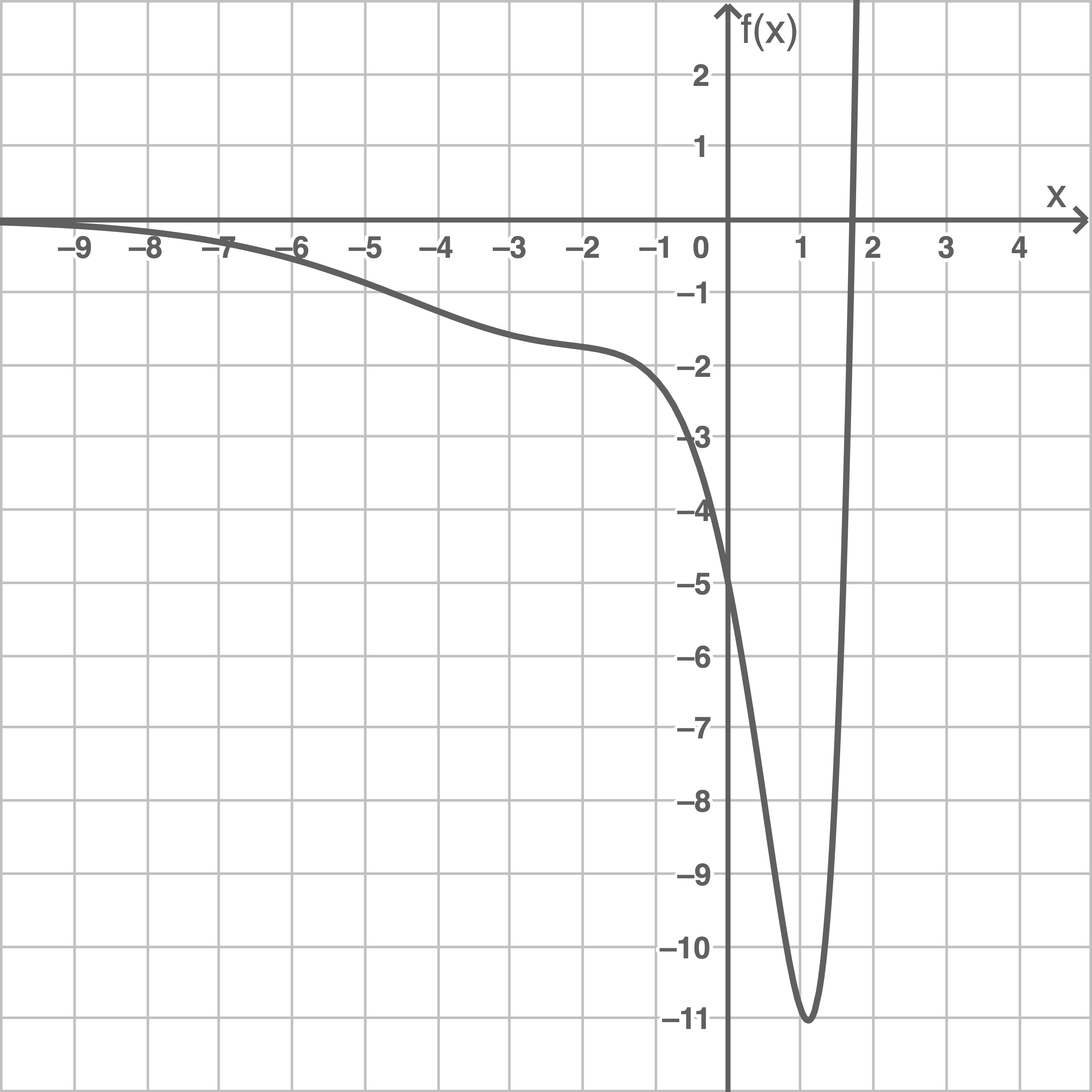
Im Folgenden darf ohne Nachweis verwendet werden: $f^{\prime}(x)=\left(x^3+3 x^2-5\right) \cdot \mathrm e ^x.$

(1)

Zeige: $f^{\prime \prime}(x)=\left(x^3+6 x^2+6 x-5\right) \cdot \mathrm e^x.$

Der Graph von $f$ besitzt genau eine Extremstelle und drei Wendestellen.

(2)

Berechne die Wendestellen der Funktion $f$ auf drei Nachkommastellen gerundet.

Für $z\gt 0$ ist $P_z(z \mid f(z))$ ein Punkt auf dem Graphen von $f.$ Er bildet zusammen mit dem Koordinatenursprung $O(0 \mid 0)$ und dem Punkt $Q_z(z \mid 0)$ ein Dreieck $O P_z Q_z.$

(3)

Bestimme den Flächeninhalt des Dreiecks $O P_z Q_z,$ wenn für $P_z$ der Tiefpunkt des Graphen von $f$ gewählt wird.

(3 + 3 + 3 Punkte)

(1)

Der folgende Ansatz eignet sich zur Bestimmung einer Stammfunktion $F$ von $f:$

$F(x)=\left(a \cdot x^3+b \cdot x^2+c \cdot x+d\right) \cdot \mathrm e ^x;$ $\quad a, b, c, d \in \mathbb{R},$ $\quad a \neq 0 .$

Berechne $F^{\prime}(x)$ und ermittle durch einen Vergleich mit $f(x)$ ein lineares Gleichungssystem für die Koeffizienten $a, b, c, d.$

[Die Berechnung der Koeffizienten ist nicht erforderlich.]

Die Gleichung einer Stammfunktion $F$ der Funktion $f$ lautet:

$F(x)=\left(x^3-3 x^2+6 x-11\right) \cdot \mathrm e ^x .$

(2)

Bestimme rechnerisch den Inhalt der Fläche, die vom Graphen der Funktion $f$ und den Koordinatenachsen im 4. Quadranten eingeschlossen wird.

(3)

Für $z \neq 0$ hat die Gleichung $\displaystyle\int_0^z f(x)\; \mathrm d x=0$ nur die Lösung $z \approx 2,271.$

Interpretiere die Lösung geometrisch.

(4)

Für $x \leq 0$ begrenzen die beiden Koordinatenachsen und der Graph von $f$ im 3. Quadranten eine Fläche mit endlichem Flächeninhalt, die nach links unendlich weit ausgedehnt ist.

Ermittle den Flächeninhalt dieser Fläche.

(5)

Die Punkte $O(0 \mid 0), N(-5 \mid 0), Y(0 \mid-5)$ bilden ein Dreieck $O N Y.$ Der Graph der Funktion $f$ verläuft teilweise innerhalb des Dreiecks und schließt mit der Seite $\overline{N Y}$ eine Fläche $A$ ein.

(i)

Zeichne die Fläche $A$ in Abbildung 1 ein.

(ii)

Bestimme den Flächeninhalt der Fläche $A.$

(5 + 3 + 3 + 3 + 6 Punkte)

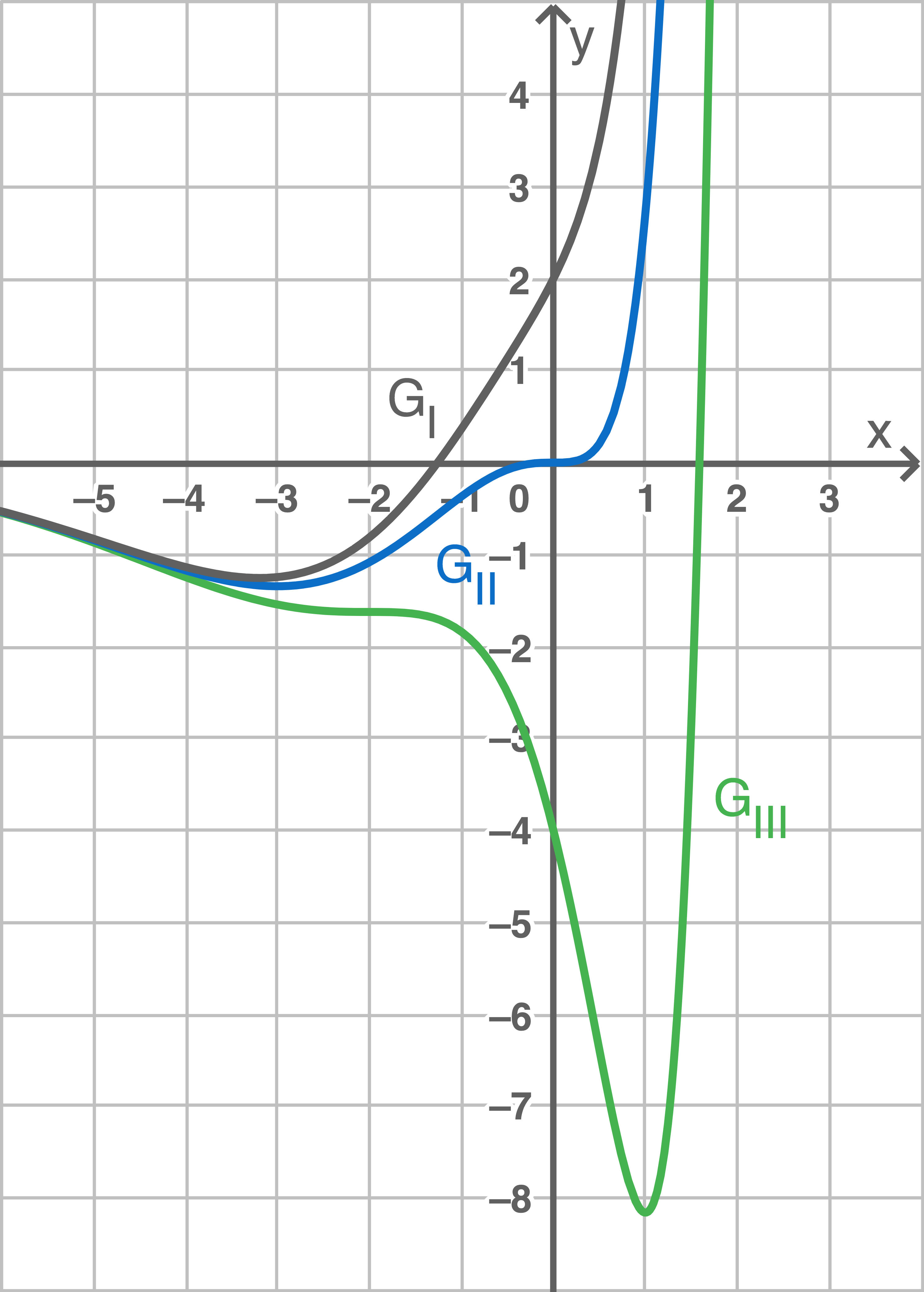
Gegeben ist die Schar der in $\mathbb{R}$ definierten Funktionen $f_k$ durch die Funktionsgleichung

$f_k(x)=\left(x^3+k\right) \cdot \mathrm e ^x$ mit $k \in \mathbb{R}.$

Die Funktion $f_{-5}$ stimmt mit der Funktion $f$ überein.

Die folgende Abbildung zeigt drei Graphen $G_I, G_{I I}, G_{I I I}$ der Schar für drei verschiedene Parameter $k_I, k_{I I}, k_{I I I}.$

Abbildung 2

(1)

Gib die zugehörigen Parameter an.

(2)

Begründe, dass jede Funktion $f_k$ der Schar genau eine Nullstelle hat.

Für die Ableitungsfunktion $f_k^{\prime}$ gilt:

$f_k^{\prime}(x)=\left(x^3+3 x^2+k\right) \cdot \mathrm e ^x,$ $\quad x \in \mathbb{R};$ $\quad k \in \mathbb{R}.$

(3)

Um die Abhängigkeit der Anzahl der Extremstellen der Funktion $f_k$ vom Parameter $k$ näher zu betrachten, wird die Funktion $h_k$ mit $h_k(x)=x^3+3 x^2+k$ auf Nullstellen untersucht.

Abbildung 3 zeigt den Graphen der Funktion $h_0$ $($ also $k=0).$

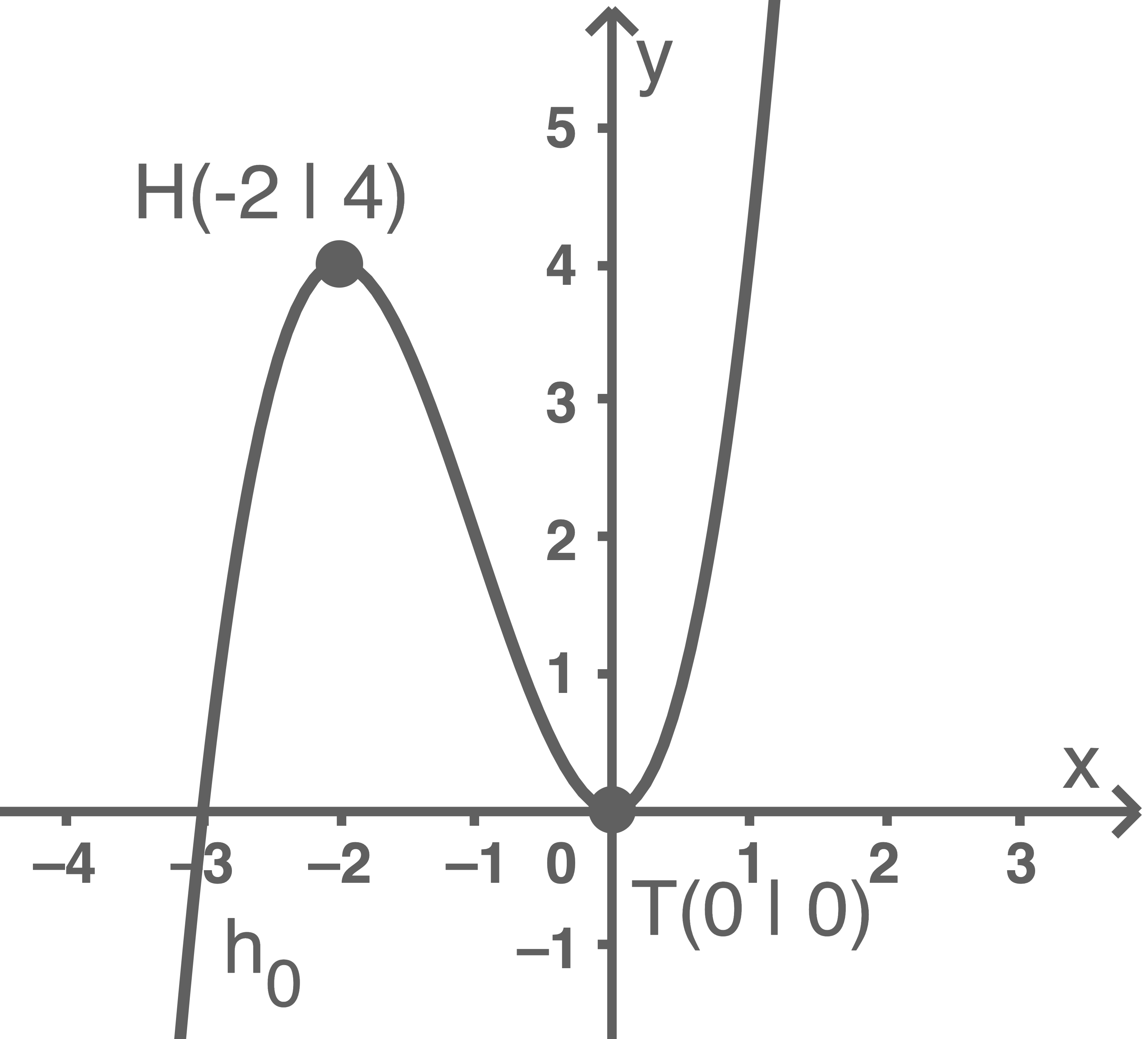
Abbildung 3

(i)

Gib anhand von Abbildung 3 die Anzahl der Nullstellen der Funktion $h_k$ in Abhängigkeit vom Parameter $k$ an.

(ii)

Begründe die Richtigkeit der folgenden drei Aussagen:

S1: Für jedes $k \gt 0$ hat die Funktion $f_k$ genau eine Extremstelle.

S2: Es gibt keine Funktion $f_k,$ die mehr als drei Extremstellen hat.

S3: Es gibt keine Funktion $f_k,$ die genau zwei Extremstellen hat.

(2 + 2 + 7 Punkte)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

(1)

$\(f$

Produktregel anwenden:

Rechenweg anzeigen

$\( f$

(2)

Notwendige Bedingung für Wendestellen:

$\(\begin{array}[t]{rll} f$

Mit dem solve-Befehl des GTRs ergeben sich:

$x_{W_1}\approx -4,361$

$x_{W_2}\approx -2,167$

$x_{W_3}\approx 0,529$

In der Aufgabenstellung ist die Existenz der Wendestellen gegeben, weshalb die hinreichende Bedingung für Wendestellen nicht mehr geprüft werden muss.

(3)

Mit der graphischen Analyse des GTRs werden die Koordinaten des Tiefpunkts ermittelt.

$T(1,1 \mid -11)$

Es gilt $z\approx 1,1$ und somit folgen die Koordinaten von $Q_z$ mit $Q_{1,1}(1,1 \mid 0).$

Hilfsskizze zum besseren Verständnis

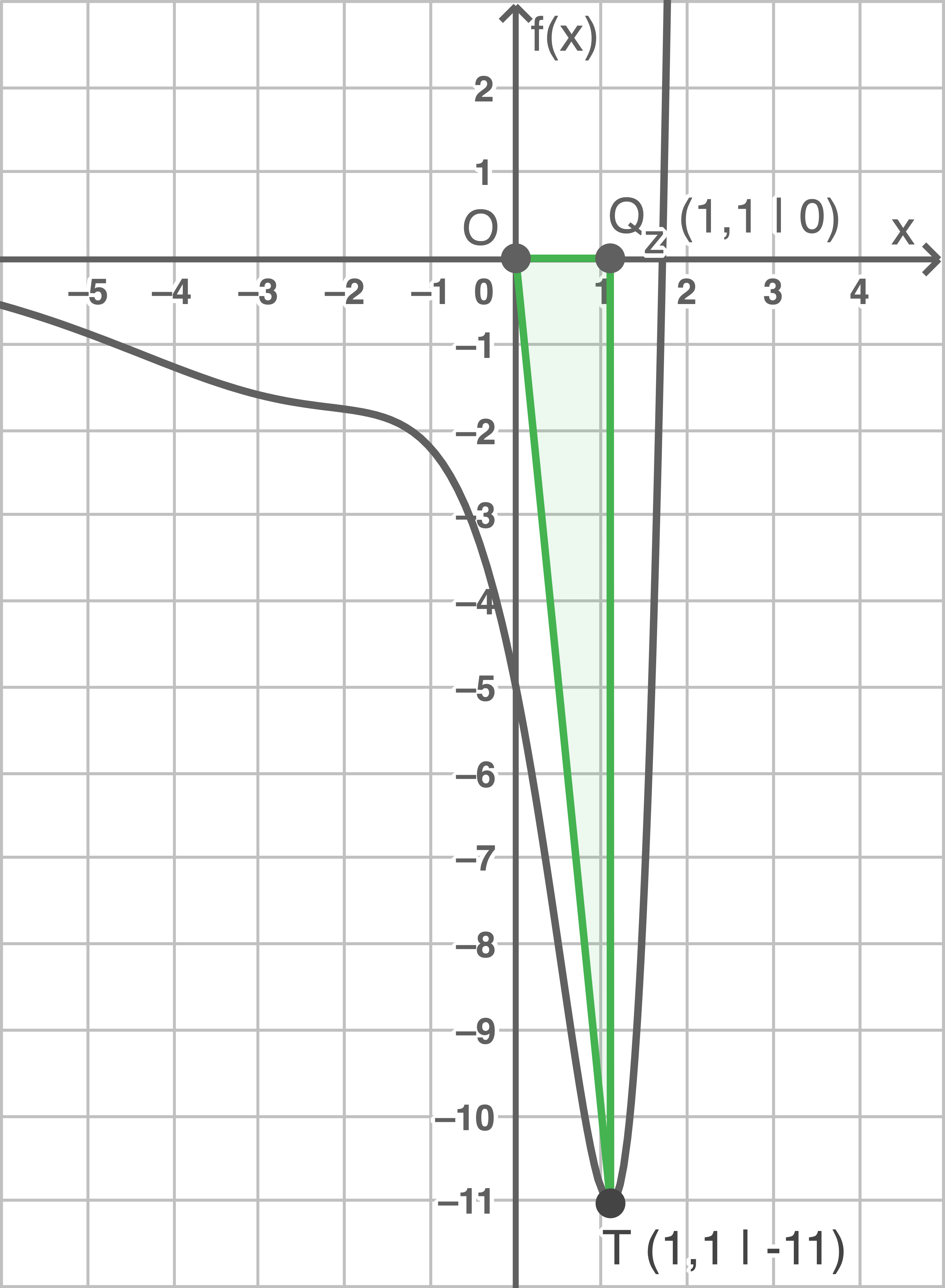Beim Dreieck $OP_{1,1}Q_{1,1}$ handelt es sich um ein rechtwinkliges Dreieck. Der Inhalt der Dreiecksfläche ergibt sich zu:

$A_D\approx \dfrac{1}{2}\cdot 1,1\cdot 11 = 6,05 \;\text{[FE]}$

(1)

$F(x)=(a\cdot x^3+b\cdot x^2+c\cdot x+d)\cdot \mathrm e^x$

$f(x)=(x^3-5)\cdot \mathrm e^x$

Ansatz ableiten mittels Produktregel und ausklammern ergibt:

Rechenweg anzeigen

$\( F$

Koeffizientenvergleich mit $f(x)$ ergibt:

$a=1$

$b+3a =0$

$c+2b =0$

$d+c=-5$

Daraus ergibt sich das LGS:

$\begin{vmatrix} a&=& 1 \\ b+3a&=& 0 \\ c+2b&=& 0 \\ d+c&=& -5 \end{vmatrix}$

(2)

Schnittstelle des Graphen von $f$ mit der $x$ -Achse bestimmen:

$f(x)=0$ wird mit dem solve-Befehl des GTRs gelöst. Es folgt $x= \sqrt[3]{5}.$

Alternativ kann auch die Nullstelle von $f$ mit der graphischen Analyse des GTRs bestimmt werden.

Der Inhalt der Fläche, die vom Graphen der Funktion $f$ und den Koordinatenachsen eingeschlossen wird, ergibt sich zu:

$\begin{array}[t]{rll} A_D&=& \displaystyle\int_0^{\sqrt[3]{5}} f(x) \; \mathrm d x \\[5pt] &=& F(\sqrt[3]{5})-F(0) \\[5pt] &\approx & -13,947 \end{array}$

Der Flächeninhalt beträgt ungefähr $13,947\,\text{FE}.$

(3)

Das Flächenstück, das der Graph von $f$ mit den Koordinatenachsen unterhalb der $x$ -Achse im 4. Quadranten einschließt, ist genauso groß wie das Flächenstück oberhalb der $x$ -Achse, das im Bereich von $x=\sqrt[3]{5}$ bis $x \approx 2,271$ zwischen dem Graphen von $f$ und der $x$ -Achse liegt.

(4)

Der gesuchte Flächeninhalt wird durch den Wert eines uneigentlichen Integrals beschrieben:

Rechenweg anzeigen

$\displaystyle\int_{-\infty}^0 f(x)\;\mathrm d x=...$

Der Flächeninhalt beträgt $11 \;\text{[FE]}.$

(5)

(i)

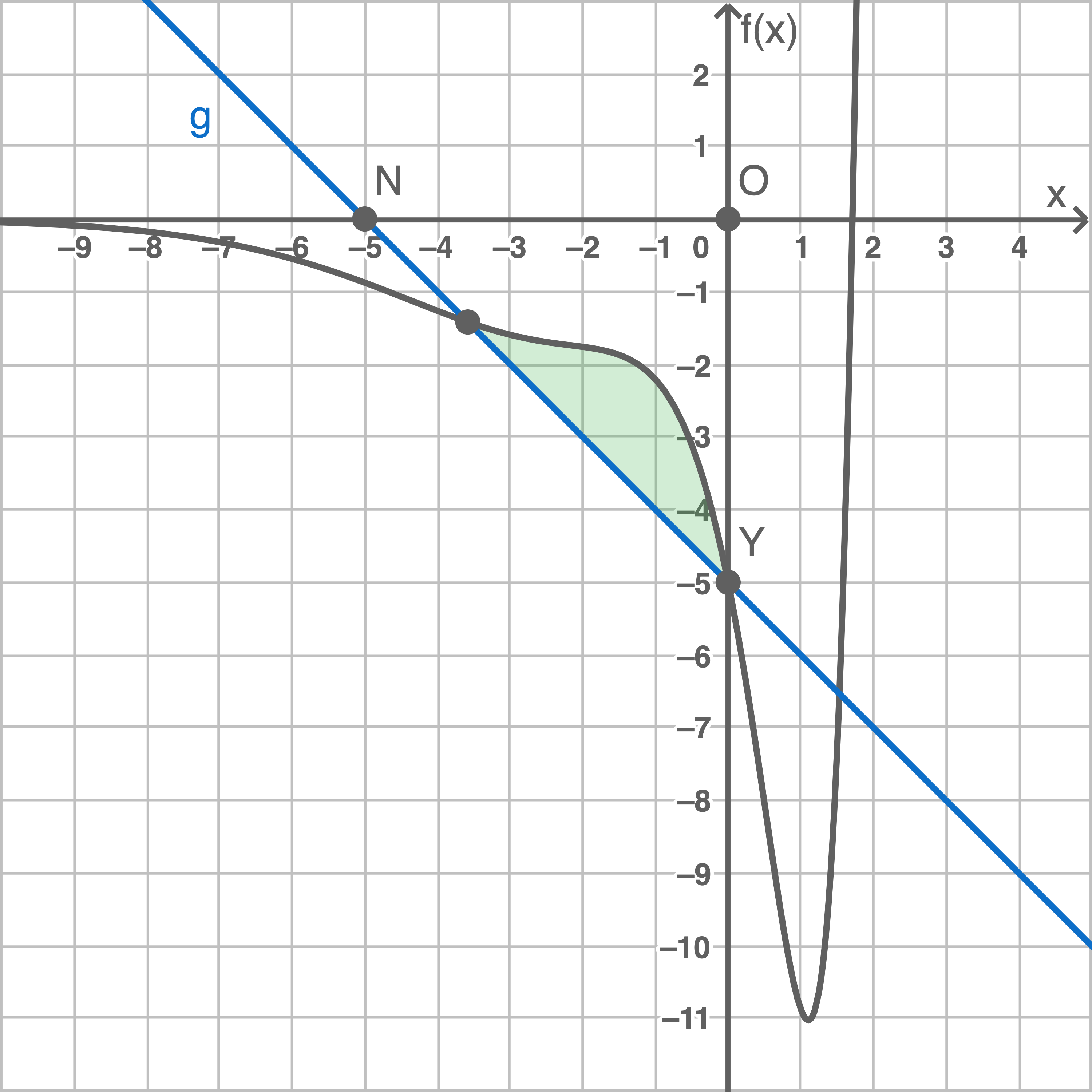
(ii)

Die Dreieckseite $\overline{N Y}$ ist Teil der Geraden mit der Gleichung $y_g=-x-5.$

Die Geradengleichung wird graphisch anhand der Abbildung bestimmt oder alternativ mit Hilfe des GTRs.

Schnittstelle von $g$ und $f$ bestimmen:

Mit dem GTR ergibt sich für $x\lt0:$ $x \approx-3,582.$

Der gesuchte Flächeninhalt lässt sich mit Hilfe eines Integrals bestimmen.

$\begin{array}[t]{rll} A&=&\displaystyle\int_{-3,582}^0(f(x)-y_g)\;\mathrm d x \\[5pt] &=&\displaystyle\int_{-3,582}^0(f(x)-(-x-5))\;\mathrm d x \end{array}$

Mit dem GTR ergibt sich $A\approx 3,748\,\text{[FE]}.$

(1)

$k_I=2, k_{I I}=0, k_{I I I}=-4$ .

(2)

$\begin{array}[t]{rll} f_k(x)&=& 0\\[5pt] (x^3+k)\cdot \mathrm e^x=& 0 \end{array}$

Da stets $\mathrm e^x \neq 0$ für alle $x \in \mathbb{R},$ muss $x^3+k=0$ sein.

Daraus folgt:

$\begin{array}[t]{rll} x^3+k&=&0 &\quad \scriptsize \mid\; -k\\[5pt] x^3&=& -k &\quad \scriptsize \mid\; \sqrt[3]{\;}\\[5pt] x&=&\sqrt[3]{-k} \end{array}$

Die Gleichung hat für alle $k \in \mathbb{R}$ genau eine Lösung: $x=-\sqrt[3]{k}$ für $k \geq 0$ bzw. $x=\sqrt[3]{-k}$ für $k \lt 0.$

(3)

(i)

Liegt der Hochpunkt oder der Tiefpunkt von $h_0$ auf der $x$ -Achse, gibt es genau zwei Nullstellen, nämlich für $k=0$ oder $k=-4.$

Es existiert genau eine Nullstelle für $k\gt 0$ oder $k\lt -4.$

Es existieren genau drei Nullstellen für $-4\lt k\lt 0.$

(ii)

Aussage S1: Für $k\gt 0$ hat die Funktion $h_k$ und damit auch die Funktion $f_k{ }^{\prime}$ genau eine Nullstelle mit Vorzeichenwechsel.
$f_k$ hat daher genau eine Extremstelle.

Aussage S2: Die Funktion $h_k$ kann als Polynomfunktion vom Grad 3 maximal drei Nullstellen haben. Wegen der notwendigen Bedingung $f_k{ }^{\prime}(x)=0$ für Extremstellen kann es nicht mehr als drei Extremstellen für die Funktion $f_k$ geben.

Aussage S3: Die Funktion $h_k$ hat nur für $k=0$ oder $k=4$ zwei Nullstellen. Dabei handelt es sich um eine Nullstelle mit und eine Nullstelle ohne Vorzeichenwechsel. Deshalb gibt es in diesen Fällen nur eine Extremstelle und eine Sattelstelle für die Funktion $f_k.$
[Aus der Abbildung ist ersichtlich, dass im Falle von genau drei Nullstellen jeweils ein Vorzeichenwechsel vorliegt und dann drei Extremstellen existieren.]

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?