Aufgabe 3

Das Gebäude eines Museums kann modellhaft durch den abgebildeten Körper $ABCDEFG$ dargestellt werden.
Die obere Etage des Museums entspricht dabei der Pyramide $DEFG,$ die untere Etage dem Körper $ABCDEF,$ der Teil der Pyramide $DEFS$ ist.
Die Ebene, in der das Dreieck $ABC$ liegt, beschreibt die horizontale Oberfläche des Untergrunds. Das Dreieck $DEF$ liegt parallel zu dieser Ebene.
In einem kartesischen Koordinatensystem gilt für die Lage einiger der genannten Punkte:

$A(-5\mid 5\mid 0),$ $B(-5\mid 25\mid 0),$ $D(0\mid 0\mid 15),$ $E(0\mid 30\mid 15),$ $F(-25\mid 5\mid 15)$ und $G(-10\mid 10\mid 35).$

Eine Längeneinheit im Koordinatensystem entspricht $1\,\text{m}$ in der Realität.

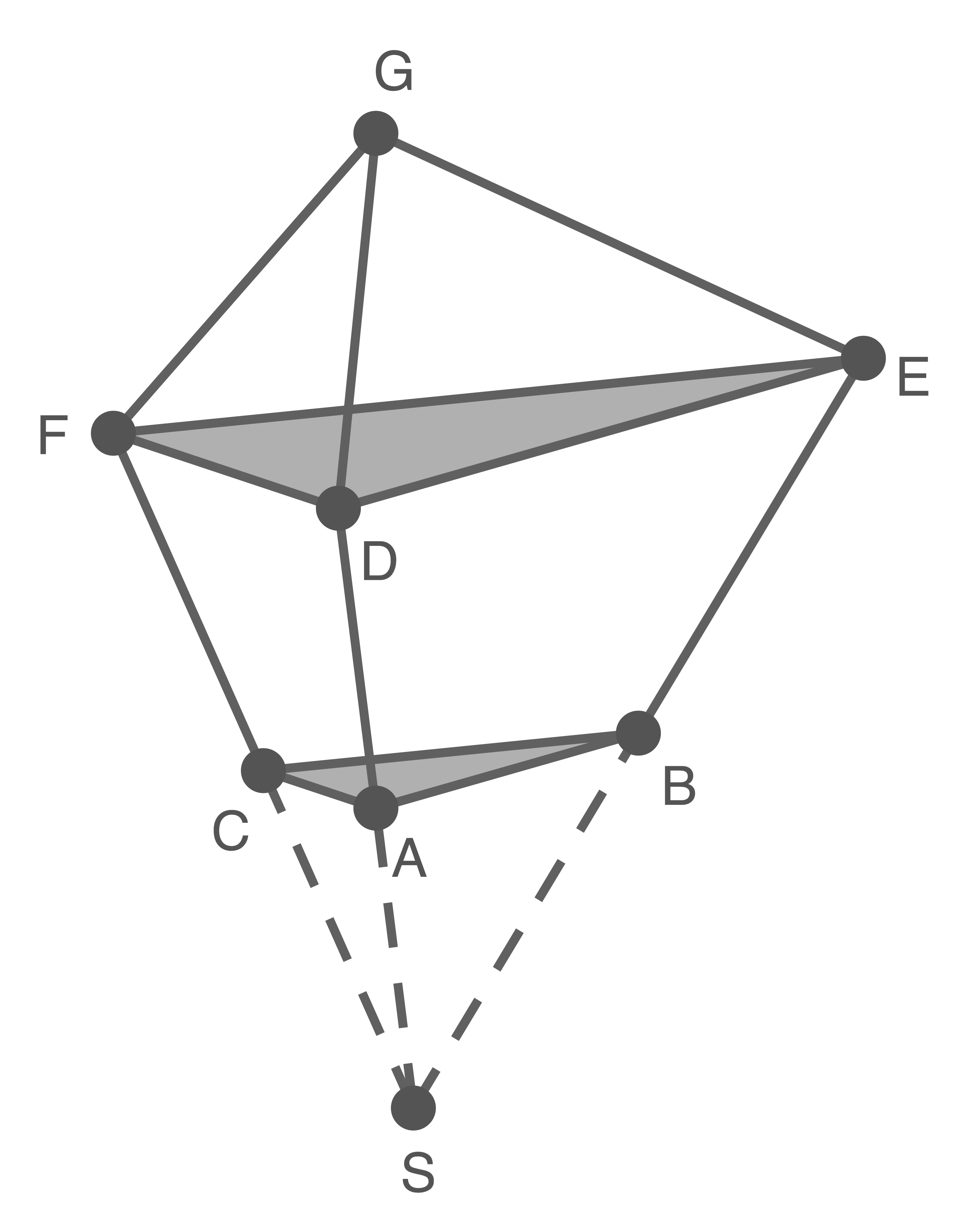
Abbildung 1

Die folgenden Rechnungen zeigen ein mögliches Vorgehen zur Ermittlung der Koordinaten von $S:$

$\pmatrix{0\\0\\15}+r \pmatrix{-5\\5\\-15} = \pmatrix{0\\30\\15} + s \pmatrix{-5\\-5\\-15} \Leftrightarrow r=s=3,$

$\pmatrix{0\\0\\15}+3 \pmatrix{-5\\5\\-15} = \pmatrix{-15\\15\\-30}$

d.h. $S(-15\mid 15\mid -30).$

Erläutere das dargestellte Vorgehen.

(5 Punkte)

(1)

Weise nach, dass die Bodenfläche der oberen Etage nicht rechtwinklig ist.

(2)

Bestimme für das Dreieck $DEF$ die Größe des Innenwinkels $\epsilon$ bei $E$ sowie die Länge der Höhe $h$ zur Seite $\overline{EF}.$
[Zur Kontrolle: $\epsilon = 45^{\circ};$ $h=15\sqrt{2}$ ]

(3)

Begründe, dass der Abstand des Punktes $G$ zur Ebene durch $DEF$ direkt aus den Koordinaten der entsprechenden Punkte ermittelt werden kann, und gib diesen Abstand an.

(4)

Für die obere Etage wird eine Anlage zur Entfeuchtung der Luft installiert, die für $100\,\text{m}^3$ Rauminhalt eine elektrische Leistung von $0,8$ Kilowatt benötigt.
Weise nach, dass für den Betrieb der Anlage eine Leistung von $25$ Kilowatt ausreichend ist.

(4 + 5 + 2 + 4 Punkte)

(1)

Weise nach, dass die Gerade $AG$ und die Ebene, in der das Dreieck $DEF$ liegt, sich im Punkt $R\left(-\dfrac{50}{7}\,\bigg \vert \, \dfrac{50}{7}\,\bigg \vert \, 15\right)$ schneiden.

(2)

Bestimme eine Koordinatenform der Ebene $U,$ in der das Dreieck $EFG$ liegt.
[Zur Kontrolle: $U:\, 2x_1-2x_2-x_3 = -75.$ ]

(3)

An einer Metallstange, die durch die Strecke $\overline{RG}$ dargestellt wird, ist im Punkt $Q$ ein Scheinwerfer befestigt, dessen Größe vernachlässigt werden soll. Der Scheinwerfer beleuchtet aus einer Entfernung von $5\,\text{m}$ diejenige Wand, die im Modell durch das Dreieck $EFG$ dargestellt wird.
Zeige, dass der Punkt $Q$ mit den Koordinaten $Q\left(-\dfrac{95}{11}\,\bigg \vert \, \dfrac{95}{11}\,\bigg \vert \, \dfrac{280}{11}\right)$ auf der Strecke $\overline{RG}$ liegt und einen Abstand von $5\,\text{m}$ zur Ebene $U$ hat.

(4 + 3 + 8 Punkte)

Der seitliche Eingang des Museums wird durch das Viereck $ABED$ modelliert. Der Architekt plant für diesen Bereich eine dreieckige Überdachung. Eine mögliche Überdachung wird durch das Dreieck $DHE$ modelliert. Diese Überdachung ist in der Abbildung 2, allerdings von einer anderen Seitenansicht als in der Abbildung 1, dargestellt.

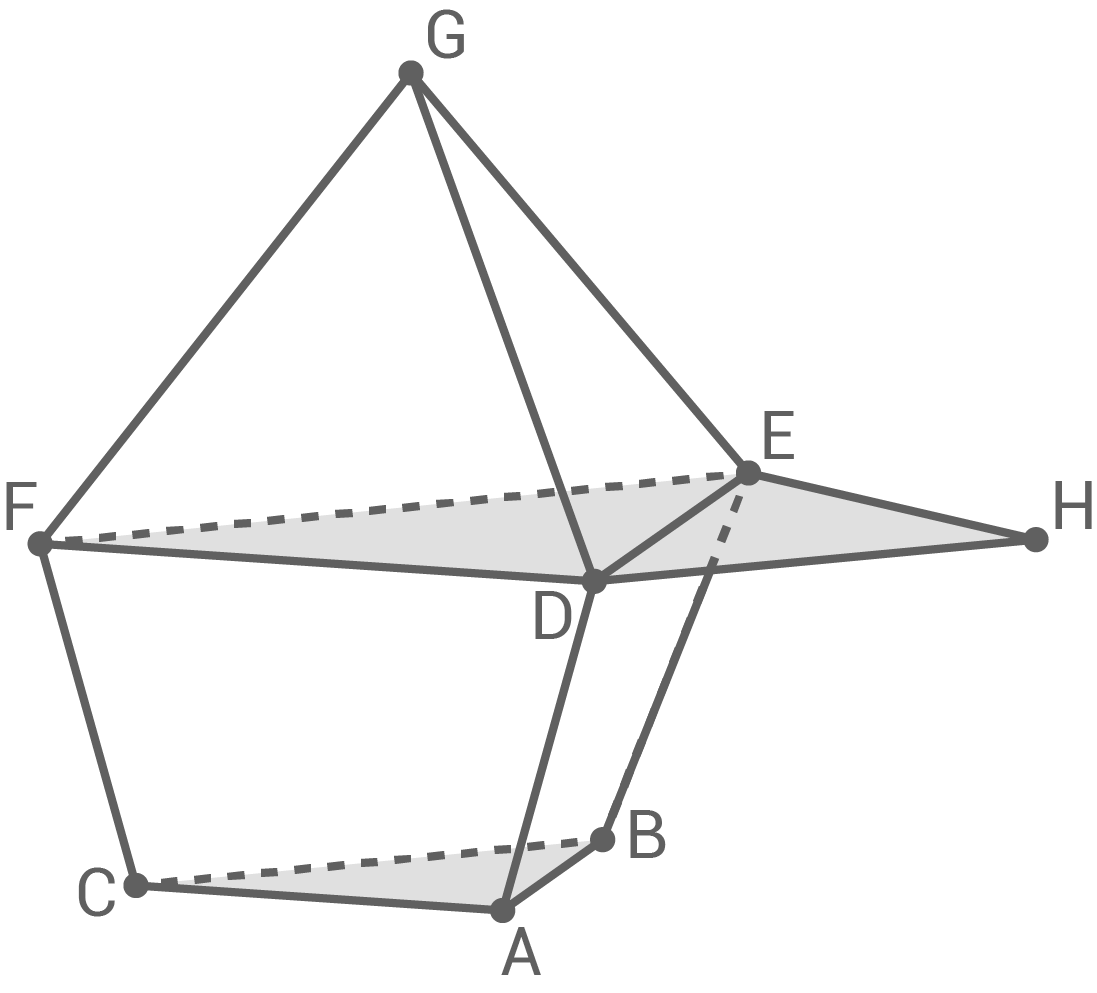
Abbildung 2

Die Planung sieht vor, dass das Dreieck $DEH$ in der gleichen Ebene wie das Dreieck $DEF$ liegt. Des Weiteren sollen die Koordinaten des Punktes $H$ so gewählt werden, dass das Dreieck $DEH$ ein gleichschenkliges Dreieck mit der Basis $\overline{DE}$ ist.
Beurteile die Aussage, dass der Ortsvektor des Punktes $H$ folgende Gleichung erfüllt:

$\overline{OH}$ $= \pmatrix{0\\15\\15} + a\cdot \pmatrix{1\\0\\0}$ $= \pmatrix{a\\15\\15};$ $a\in \mathbb{R}.$

(5 Punkte)

Der Punkt $S$ ist der Schnittpunkt der drei Geraden durch die Punkte $F$ und $C,$ $D$ und $A,$ $E$ und $B.$

Es genügt den Schnittpunkt zweier Geraden zu bestimmen. In der dargestellten Rechnung werden die beiden Parameterdarstellungen der Geraden durch die Punkte $D$ und $A$ mit dem Geradenparameter $r$ und durch die Punkte $E$ und $B$ mit dem Geradenparameter $s$ gleichgesetzt.
Diese Gleichung liefert eine Lösung für $r$ und $s.$ Der Wert für $r$ wird in die Geradengleichung durch die Punkte $D$ und $A$ eingesetzt und liefert den Ortsvektor des Schnittpunkts.
Daraus ergeben sich die Koordinaten des Punktes $S.$

(1)

$\begin{array}[t]{rll} \overrightarrow{DE}\circ \overrightarrow{DF}&=& \pmatrix{0\\30\\0} \circ \pmatrix{-25\\5\\0} \\[5pt] &=& 0\cdot (-25) + 30\cdot 5 + 0\cdot 0 \\[5pt] &=& 150 \neq 0 \\[10pt] \overrightarrow{DE}\circ \overrightarrow{EF}&=& \pmatrix{0\\30\\0} \circ \pmatrix{-25\\-25\\0} \\[5pt] &=& 0\cdot (-25) + 30\cdot (-25) + 0\cdot 0 \\[5pt] &=& -750 \neq 0 \\[10pt] \overrightarrow{DF}\circ \overrightarrow{EF}&=& \pmatrix{-25\\5\\0} \circ \pmatrix{-25\\-25\\0} \\[5pt] &=& (-25)\cdot (-25) + 5\cdot (-25) + 0\cdot 0 \\[5pt] &=& 500 \neq 0 \\[10pt] \end{array}$

Die Bodenfläche $DEF$ ist also nicht rechtwinklig.

(2)

Größe des Innenwinkels

$\begin{array}[t]{rll} \cos (\varepsilon) &=& \dfrac{\left|\overrightarrow{DE} \circ \overrightarrow{EF} \right|}{\left| \overrightarrow{DE}\right| \cdot \left|\overrightarrow{EF}\right|} \\[5pt] \cos (\varepsilon) &=& \dfrac{\left|\pmatrix{0\\30\\0} \circ \pmatrix{-25\\-25\\0} \right|}{\left| \pmatrix{0\\30\\0}\right| \cdot \left|\pmatrix{-25\\-25\\0} \right|} \\[5pt] \cos (\varepsilon) &=& \dfrac{750}{\sqrt{0^2 +30^2 +0^2 }\cdot \sqrt{(-25)^2 +(-25)^2 +0^2} } \\[5pt] \cos (\varepsilon)&=& \dfrac{750}{30\cdot \sqrt{1250}} \\[5pt] \varepsilon&=& 45^{\circ} \\[5pt] \end{array}$

Der Innenwinkel des Dreiecks $DEF$ bei $E$ ist $45^{\circ}$ groß.

Bezeichne mit $P$ den Punkt, in dem die Hhe $h$ auf die Seite $\overline{EF}$ trifft.
Zwei der Innenwinkel des Dreiecks $DEP$ sind bekannt:

Der Winkel $\varepsilon$ bei $E$ hat die Größe $45^{\circ}.$
Der Innenwinkel bei $P$ beträgt aufgrund der Eigenschaften der Höhe $90^{\circ}.$

Der dritte Winkel $\alpha$ bei $D$ muss also aufgrund der Winkelsumme $180^{\circ}$ eines Dreiecks folgende Größe haben:

$\alpha = 180^{\circ} - 90^{\circ}-45^{\circ} = 45^{\circ}$

Die beiden Innenwinkel bei $E$ und $D$ sind also gleichgroß, sodass es sich bei $DEP$ um ein gleichschenkliges Dreieck handelt. Dadurch sind auch die beiden Seiten $\overline{PE}$ und $\overline{PD}$ gleich lang: $h= \overline{PE}=\overline{PD}.$
Die Länge der Hypotenuse $\overline{DE}$ kannst du mit dem Vektorbetrag des zugehörigen Vebindungsvektors berechnen:

$\begin{array}[t]{rll} \overline{DE}&=& \left| \overrightarrow{DE}\right| \\[5pt] &=& \left| \pmatrix{ 0\\30\\0}\right| \\[5pt] &=& \sqrt{0^2+30^2 +0^2} \\[5pt] &=& 30 \end{array}$

Mit dem Satz des Pythagoras folgt dann aufgrund der Gleichschenkligkeit:

$\begin{array}[t]{rll} \overline{DE}&=& h^2+h^2 \\[5pt] 30^2&=& 2\cdot h^2&\quad \scriptsize \mid\;:2 \\[5pt] 450&=& h^2&\quad \scriptsize \mid\;\sqrt{\,} \\[5pt] 15\sqrt{2}&=& h \end{array}$

Die Höhe $h$ ist $15\sqrt{2}$ Längeneinheiten lang.

(3)

Die drei Punkte $D,$ $E$ und $F$ besitzen die gleiche $x_3$ -Koordinate. Da eine Ebene durch drei unterschiedliche Punkte bereits vollständig bestimmt ist, müssen alle Punkte in der Ebene die gleiche $x_3$ -Koordinate besitzen. Bei der Ebene durch die drei Punkte $D,$ $E$ und $F$ handelt es sich also um eine zur $x_1x_2$ -Ebene parallele Ebene.
Der Abstand eines Punkts zu dieser Ebene kann daher über die Differenz der $x_3$ -Koordinaten berechnet werden. Die $x_3$ -Koordinate von $G$ ist $35,$ die $x_3$ -Koordinate von $DEF$ ist $15.$

$d = 35 -15 = 20$

Der Abstand von $G$ zur Ebene durch $DEF$ beträgt also $20\,\text{LE}.$

(4)

Die obere Etage hat die Form einer Pyramide. Die Höhe der Pyramide entspricht dem Abstand von $G$ zur Ebene durch $DEF,$ welchen du eben berechnet hast:

$h_{\text{Pyramide}} = d = 20\,\text{m}$

1. Schritt: Inhalt der Bodenfläche berechnen

Die Bodenfläche der oberen Etage ist das Dreieck $DEF,$ dessen Höhe zur Seite $\overline{EF}$ du bereits berechnet hast:

$h = 15\sqrt{2}\,\text{m}$

Die Länge der Seite $\overline{EF}$ kannst du wieder über den Vektorbetrag berechnen.

$\begin{array}[t]{rll} \overline{EF}&=& \left|\overrightarrow{EF} \right| \\[5pt] &=& \left|\pmatrix{-25\\-25\\0} \right| \\[5pt] &=& \sqrt{(-25)^2 +(-25)^2 + 0^2} \\[5pt] &=& 25\sqrt{2} \\[5pt] \end{array}$

Für den Flächeninhalt der Bodenfläche gilt daher:

$\begin{array}[t]{rll} A &=& \frac{1}{2}\cdot 15\sqrt{2}\,\text{m} \cdot 25\sqrt{2}\,\text{m} \\[5pt] &=& 375\,\text{m}^2 \end{array}$

2. Schritt: Volumen berechnen

Mit der Formel für das Volumen einer Pyramide folgt:

$\begin{array}[t]{rll} V&=& \frac{1}{3}\cdot h_{\text{Pyramide}} \cdot A \\[5pt] &=& \frac{1}{3}\cdot 20\,\text{m} \cdot 375\,\text{m}^2 \\[5pt] &=& 2.500\,\text{m}^3 \\[5pt] \end{array}$

Das Volumen der oberen Etage beträgt $2.500\,\text{m}^3.$ Es werden demnach $25\cdot 0,8$ Kilowatt benötigt. $25$ Kilowatt reichen also aus.

(1)

Die Gerade $AG$ kann durch folgende Gleichung beschrieben werden:

$\begin{array}[t]{rll} AG:\quad \overrightarrow{x}&=& \overrightarrow{OA} + r\cdot \overrightarrow{AG} \\[5pt] &=& \pmatrix{-5\\5\\0} + r\cdot \pmatrix{-5\\5\\35} \end{array}$

Da das Dreieck $DEF$ in einer zur $x_1x_2$ -Ebene parallelen Ebene liegt und die Punkte $D,$ $E$ und $F$ alle die $x_3$ -Koordinate $15$ haben, kann die Ebene $E,$ in der das Dreieck $DEF$ liegt, durch folgende Gleichung beschrieben werden:

$E:\, x_3 = 15$

Die $x_3$ -Koordinate der Punkte auf der Geraden $AG$ ist $35r.$ Einsetzen in die Ebenengleichung liefert:

$\begin{array}[t]{rll} x_3&=& 15 &\quad \scriptsize \mid\;x_3 = 35r \\[5pt] 35r&=& 15 &\quad \scriptsize \mid\;:35 \\[5pt] r&=& \frac{3}{7} \end{array}$

Einsetzen in die Geradengleichung liefert den Ortsvektor des Schnittpunkts $R:$

$\begin{array}[t]{rll} \overrightarrow{OR}&=& \pmatrix{-5\\5\\0} + \frac{3}{7}\cdot \pmatrix{-5\\5\\35} \\[5pt] &=& \pmatrix{-\frac{50}{7}\\ \frac{50}{7}\\ 15} \\[5pt] \end{array}$

Die Koordinaten des Schnittpunkts der Geraden $AG$ und der Ebene, in der das Dreieck $DEF$ liegt, lauten $R\left(-\frac{50}{7}\mid \frac{50}{7}\mid 15\right).$

(2)

Ein Normalenvektor von $U$ kann über das Kreuzprodukt zweier Verbindungsvektoren der drei Punkte $E,$ $F$ und $G$ bestimmt werden:

$\begin{array}[t]{rll} \overrightarrow{n} &=& \overrightarrow{EF}\times \overrightarrow{EG} \\[5pt] &=& \pmatrix{-25\\-25\\0}\times \pmatrix{-10\\-20\\20} \\[5pt] &=& \pmatrix{-25\cdot 20 - 0\cdot (-20) \\ 0\cdot (-10) - (-25)\cdot 20 \\ (-25) \cdot (-20) - (-25)\cdot (-10)} \\[5pt] &=& \pmatrix{-500\\500\\250} \\[5pt] &=& -250\cdot \pmatrix{2\\-2\\-1} \\[5pt] \end{array}$

Für die Ebenengleichung kann nun sowohl der gekürzte Normalenvektor als auch der ursprüngliche verwendet werden. Mit einer Punktprobe mithilfe der Koordinaten eines der drei Punkte folgt:

$\begin{array}[t]{rll} U:\quad 2\cdot x_1 -2\cdot x_2 -1\cdot x_3 &=& d &\quad \scriptsize \mid\; E(0\mid 30\mid 15)\\[5pt] 2\cdot 0 -2\cdot 30 -1 \cdot 15 &=& d \\[5pt] -75&=& d \end{array}$

Eine Gleichung von $U$ in Koordinatenform lautet:

$U:\quad 2 x_1 -2 x_2 - x_3 = -75$

(3)

Die Strecke $\overline{RG}$ kann mit $t\in[0;1]$ durch folgende Gleichung beschrieben werden:

$\begin{array}[t]{rll} \overline{x}&=& \overrightarrow{OR} + t\cdot \overrightarrow{RG} \\[5pt] &=& \pmatrix{-\frac{50}{7}\\ \frac{50}{7}\\15} + t\cdot \pmatrix{-\frac{20}{7}\\ \frac{20}{7}\\ 20} \\[5pt] \end{array}$

Gleichsetzen mit dem Ortsvektor von $Q$ liefert:

$\begin{array}[t]{rll} \pmatrix{-\frac{95}{11}\\\frac{95}{11}\\\frac{280}{11}} &=& \pmatrix{-\frac{50}{7}\\ \frac{50}{7}\\15} + t\cdot \pmatrix{-\frac{20}{7}\\ \frac{20}{7}\\ 20} &\quad \scriptsize \mid\; - \pmatrix{-\frac{50}{7}\\ \frac{50}{7}\\15} \\[5pt] \pmatrix{-\frac{115}{77} \\\frac{115}{77} \\ \frac{115}{11} }&=& t\cdot \pmatrix{-\frac{20}{7}\\ \frac{20}{7}\\ 20} \\[5pt] \end{array}$

Für die erste Zeile dieser Gleichung gilt nun:

$\begin{array}[t]{rll} -\frac{115}{77} &=& -\frac{20}{7}t &\quad \scriptsize\mid \; :\left(-\frac{20}{7} \right) \\[5pt] \frac{23}{44}&=& t \\[5pt] \end{array}$

Durch eine Probe ergibt sich, dass die anderen beiden Zeilen für diesen Wert ebenfalls erfüllt sind. Es gilt also:

$\overrightarrow{OQ} = \overrightarrow{OR} + t\cdot \overrightarrow{RG}$ für $t = \frac{23}{44}.$ Da der Wert von $t$ größer als Null und kleiner als eins ist, muss $Q$ auf der Strecke $\overline{RG}$ liegen.

Der Abstand zwischen der Ebene $U$ und dem Punkt $Q$ kann mithilfe einer Hesseschen Normalenform von $U$ bestimmt werden:

$\begin{array}[t]{rll} U:\, \dfrac{2x_1 -2x_2 -x_3 +75}{\left|\pmatrix{2\\-2\\-1} \right|} &=& 0 \\[5pt] U:\, \dfrac{2x_1 -2x_2 -x_3 +75}{\sqrt{2^2+(-2)^2 +(-1)^2}} &=& 0 \\[5pt] U:\, \dfrac{2x_1 -2x_2 -x_3 +75}{3} &=& 0 \\[5pt] \end{array}$

Der Abstand eines Punkts $P(x_1 \mid x_2 \mid x_3)$ zu $U$ kann daher mit folgendem Term berechnet werden:

$d(P,U) = \dfrac{2x_1 -2x_2 -x_3 +75}{3}$

$\begin{array}[t]{rll} d(Q,U)&=& \dfrac{2\cdot \left(-\frac{95}{11} \right) -2\cdot \frac{95}{11} -\frac{280}{11} +75}{3} \\[5pt] &=& 5 \\[5pt] \end{array}$

Der Punkt $Q$ hat also den Abstand $5\,\text{m}$ zur Ebene $U.$

Der Punkt $H$ muss auf einer Geraden $h$ liegen, die wegen der Gleichschenkligkeit von $DEH$ senkrecht zur Strecke $\overline{DE}$ durch den Mittelpunkt $M$ der Strecke $\overline{DE}$ verläuft.
Da das Dreieck $DEH$ in der gleichen Ebene wie $DEF$ liegt, muss auch die Gerade $h$ in dieser Ebene liegen. Alle Punkte auf $h$ müssen also die $x_3$ -Koordinate $15$ besitzen.

1. Schritt: Stützvektor bestimmen

Als Stützvektor der Geraden $h$ kann der Ortsvektor von $M$ verwendet werden. Mit der entsprechenden Formel folgt:

$\overrightarrow{OM} = \frac{1}{2}\cdot \left(\overrightarrow{OD} +\overrightarrow{OE} \right) = \frac{1}{2}\cdot \left(\pmatrix{0\\0\\15} +\pmatrix{0\\30\\15} \right) = \pmatrix{0\\15\\15}$

2. Schritt: Richtungsvektor bestimmen

Da die Gerade $h$ in der Ebene $E$ mit der Gleichung $x_3=15$ liegen soll, muss auch für alle Punkte auf $h$ $x_3=15$ gelten. Der Richtungsvektor $\pmatrix{h_1\\h_2\\h_3}$ muss daher in der letzten Koordinate Null sein: $h_3 = 0,$ damit die $x_3$ -Koordinate unveränderlich ist.
Der Richtungsvektor $\pmatrix{h_1\\h_2\\0}$ muss senkrecht zu $\overline{DE}$ verlaufen, also muss das Skalarprodukt der beiden Vektoren Null ergeben:

$\begin{array}[t]{rll} \pmatrix{h_1\\h_2\\0}\circ \pmatrix{0\\30\\0}&=& 0 \\[5pt] 30h_2&=& 0 &\quad \scriptsize \mid\;:30 \\[5pt] h_2&=& 0 \end{array}$

$h_1$ kann also beliebig verändert werden. Daher liegt $H$ auf der Geraden mit der Gleichung:

$\begin{array}[t]{rll} h:\, \overrightarrow{x} &=& \overrightarrow{OM} + a\cdot \overrightarrow{h} \\[5pt] &=& \pmatrix{0\\15\\15}+ a\cdot \pmatrix{1\\0\\0} \\[5pt] &=& \pmatrix{a\\15\\15} \\[5pt] \end{array}$

Die angegebene Aussage stimmt also dahingehend, dass der Ortsvektor von $H$ die angegebene Gleichung für $a\in \mathbb{R}$ erfüllt. Allerdings läge die Überdachung betrachtet im Sachzusammenhang für $a\leq 0$ innerhalb oder zumindeste teilweise innerhalb des Gebäudes, was im Sachzusammenhang keinen Sinn ergibt.
Es sollte also auf $a \gt 0$ eingegrenzt werden.