Aufgabe 2
Aufgabenstellung
Eine Familie will ihren Bedarf an Wärmeenergie (thermischer Energie) für Heizung und Warmwasser teilweise durch eine thermische Solaranlage (kurz: Solaranlage) decken. Anhand der Angaben des Solaranlagenherstellers und der Verbrauchswerte der Familie aus dem letzten Kalenderjahr wurde das folgende Modell für ein beispielhaftes Kalenderjahr aufgestellt.
Die Leistung der Solaranlage wird durch die Funktion mit der Gleichung
mit der Gleichung
 ,
,  ,
und der thermische Leistungsbedarf der Familie (kurz: Leistungsbedarf) durch die Funktion
,
und der thermische Leistungsbedarf der Familie (kurz: Leistungsbedarf) durch die Funktion  mit der Gleichung
mit der Gleichung
 ,
,  ,
modelliert, und zwar für das Zeitintervall
,
modelliert, und zwar für das Zeitintervall ![\([0;12]\)](https://mathjax.schullv.de/5ba9b38204a320e9433651393178f89e741e0a72de8e09a0201574090d0733c6?color=5a5a5a) , das dem Kalenderjahr entspricht.
, das dem Kalenderjahr entspricht.
Dabei fasst man als Maßzahl zur Einheit
als Maßzahl zur Einheit  Monat und
Monat und  sowie
sowie  als Maßzahlen zur Einheit
als Maßzahlen zur Einheit  Kilowattstunde pro Monat [kWh/Monat] auf. (Im Modell umfasst jeder Monat
Kilowattstunde pro Monat [kWh/Monat] auf. (Im Modell umfasst jeder Monat  Tage.) Der Zeitpunkt
Tage.) Der Zeitpunkt  entspricht dem Beginn des Kalenderjahres.
entspricht dem Beginn des Kalenderjahres.
Die Graphen von und
und  sind in der Abbildung 1 unten dargestellt.
sind in der Abbildung 1 unten dargestellt.
 ist im Sachzusammenhang die aus der Solaranlage im Zeitintervall
ist im Sachzusammenhang die aus der Solaranlage im Zeitintervall ![\([a; b]\)](https://mathjax.schullv.de/55d9c86ce052c8cc565dcfb2a42d040a408cd01e6029a75d99c52b506b61c5b3?color=5a5a5a) abrufbare Energie und durch das Integral
abrufbare Energie und durch das Integral  der Energiebedarf der Familie im Zeitintervall
der Energiebedarf der Familie im Zeitintervall ![\([a; b]\)](https://mathjax.schullv.de/55d9c86ce052c8cc565dcfb2a42d040a408cd01e6029a75d99c52b506b61c5b3?color=5a5a5a) für
für  in Kilowattstunden [kWh] gegeben.
in Kilowattstunden [kWh] gegeben.
 ,
,  ,
,  ,
,
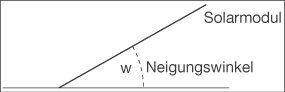
modelliert im Intervall [0;12] diese Leistung für ein Kalenderjahr, wobei der Parameter eine Kennzahl für die Neigung der Solarmodule ist. Jedem Wert des Parameters
eine Kennzahl für die Neigung der Solarmodule ist. Jedem Wert des Parameters  kann über die Gleichung
kann über die Gleichung  die Maßzahl für den entsprechenden Neigungswinkel in Grad zugeordnet werden.
die Maßzahl für den entsprechenden Neigungswinkel in Grad zugeordnet werden.
In der Abbildung 2 sind beispielhaft für zwei Werte von die Graphen der jeweils zugehörigen Funktion
die Graphen der jeweils zugehörigen Funktion  sowie der Graph von
sowie der Graph von  dargestellt.
dargestellt.
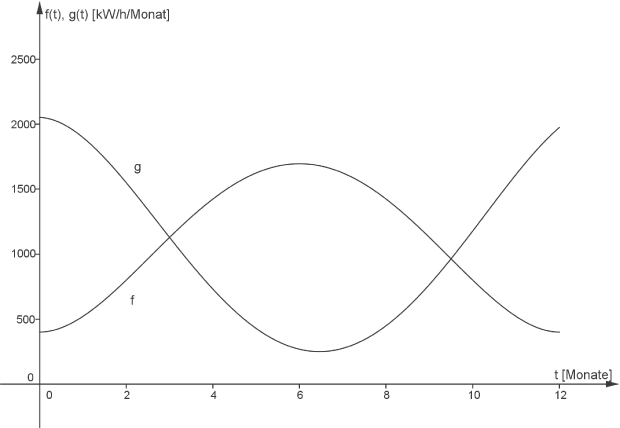 Abbildung 1
Abbildung 1
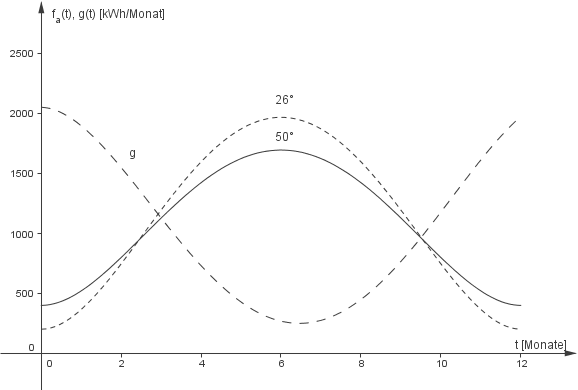 Abbildung 2
Abbildung 2
Die Leistung der Solaranlage wird durch die Funktion
Dabei fasst man
Die Graphen von
a) (1) Vergleiche die Graphen von  und
und  im Sachzusammenhang.
im Sachzusammenhang.
(5P)
(2) Bestimme den Zeitpunkt der maximalen Leistung der Solaranlage und berechne den Maximalwert.
(8P)
(3) Ermittle den Zeitpunkt im Intervall [ ], zu dem der durch
], zu dem der durch  beschriebene Leistungsbedarf der Familie innerhalb dieses Kalenderjahres am stärksten abnimmt.
beschriebene Leistungsbedarf der Familie innerhalb dieses Kalenderjahres am stärksten abnimmt.
(9P)
Durch das Integral
b) (1) Berechne den Energiebedarf der Familie für das Kalenderjahr.
(4P)
(2) Im Intervall [ ] wird der Leistungsbedarf der Familie zu jedem Zeitpunkt durch die Solaranlage gedeckt. Die den Bedarf übersteigende Leistung der Solaranlage soll in diesem Zeitraum zusätzlich zum Heizen eines Gartenpools genutzt werden.
] wird der Leistungsbedarf der Familie zu jedem Zeitpunkt durch die Solaranlage gedeckt. Die den Bedarf übersteigende Leistung der Solaranlage soll in diesem Zeitraum zusätzlich zum Heizen eines Gartenpools genutzt werden.
Ermittle die Energie, die zum Heizen des Gartenpools im Intervall [ ] zur Verfügung steht.
] zur Verfügung steht.
Ermittle die Energie, die zum Heizen des Gartenpools im Intervall [
(6P)
c) Die Leistung der Solaranlage ist abhängig von der Neigung der aufgestellten Solarmodule. Die Funktion  mit der Gleichung
mit der Gleichung

modelliert im Intervall [0;12] diese Leistung für ein Kalenderjahr, wobei der Parameter
In der Abbildung 2 sind beispielhaft für zwei Werte von
(1) Zeige, dass  eine der Funktionen
eine der Funktionen  ist, und berechne den zugehörigen Neigungswinkel
ist, und berechne den zugehörigen Neigungswinkel  der Solarmodule.
der Solarmodule.
(4P)
(2) Weise nach, dass die in einem Jahr aus der Solaranlage abrufbare Energie für  (d.h.
(d.h.  ) am größten ist.
) am größten ist.
(9P)
(3) Der Solaranlagenhersteller behauptet, dass eine Solaranlage mit einem Neigungswinkel von  den Leistungsbedarf der Familie (ohne Heizung des Gartenpools!) in dem Kalenderjahr besser deckt als eine Solaranlage mit einem Neigungswinkel von
den Leistungsbedarf der Familie (ohne Heizung des Gartenpools!) in dem Kalenderjahr besser deckt als eine Solaranlage mit einem Neigungswinkel von  .
.
Begründe diese Behauptung anhand der Graphen in Abbildung 2.
[Eine Rechnung wird hier nicht verlangt.]
Begründe diese Behauptung anhand der Graphen in Abbildung 2.
[Eine Rechnung wird hier nicht verlangt.]
(5P)
 Abbildung 1
Abbildung 1
 Abbildung 2
Abbildung 2
a)(1)
 Graphen von
Graphen von  und
und  im Sachzusammenhang vergleichen
Hier sollst du die Graphen von
im Sachzusammenhang vergleichen
Hier sollst du die Graphen von  und
und  im Sachzusammenhang vergleichen. Die Funktion
im Sachzusammenhang vergleichen. Die Funktion  modelliert die Leistung der Solaranlage, die Funktion
modelliert die Leistung der Solaranlage, die Funktion  den Leistungsbedarf der Familie. Du erkennst, dass in den Intervallen
den Leistungsbedarf der Familie. Du erkennst, dass in den Intervallen ![\(\left[0;3\right]\)](https://mathjax.schullv.de/e6ac5d60749307c17b05c9a262850c1a1312bb0bdac1077886594150a0f01657?color=5a5a5a) und
und ![\(\left[9,5;12\right]\)](https://mathjax.schullv.de/47d231a407dc5122a8184c20a6aacccc109aaeff05e0642aed51402f3d886a66?color=5a5a5a) der Graph der Funktion
der Graph der Funktion  oberhalb des Graphen von
oberhalb des Graphen von  liegt, im Intervall
liegt, im Intervall ![\(\left[3;9,5\right]\)](https://mathjax.schullv.de/a03ac5fe1f2ee83bfa4590b6a6c79fbf40a569515ebcc534bfeed1e72a1f310a?color=5a5a5a) ist es gerade andersrum und der Graph von
ist es gerade andersrum und der Graph von  liegt über dem Graphen von
liegt über dem Graphen von  . Die Graphen von
. Die Graphen von  und
und  verhalten sich gegenläufig um einen Mittelwert von ca. 1.000.
Im Sachzusammenhang lässt sich dies so deuten, dass im Winter (Intervalle
verhalten sich gegenläufig um einen Mittelwert von ca. 1.000.
Im Sachzusammenhang lässt sich dies so deuten, dass im Winter (Intervalle ![\(\left[0;3\right]\)](https://mathjax.schullv.de/e6ac5d60749307c17b05c9a262850c1a1312bb0bdac1077886594150a0f01657?color=5a5a5a) und
und ![\(\left[9,5;12\right]\)](https://mathjax.schullv.de/47d231a407dc5122a8184c20a6aacccc109aaeff05e0642aed51402f3d886a66?color=5a5a5a) ) weniger Energie produziert wird als benötigt wird und die Solaranlage den Energiebedarf nicht vollständig deckt. Im Sommer (Intervall
) weniger Energie produziert wird als benötigt wird und die Solaranlage den Energiebedarf nicht vollständig deckt. Im Sommer (Intervall ![\(\left[3;9,5\right]\)](https://mathjax.schullv.de/a03ac5fe1f2ee83bfa4590b6a6c79fbf40a569515ebcc534bfeed1e72a1f310a?color=5a5a5a) ) wird mehr Energie als benötigt produziert und der Energiebedarf wird vollständig gedeckt.
Um den Juni (
) wird mehr Energie als benötigt produziert und der Energiebedarf wird vollständig gedeckt.
Um den Juni ( ) ist die Leistung der Solaranlage maximal und der Leistungsbedarf minimal. Um den Jahreswechsel (
) ist die Leistung der Solaranlage maximal und der Leistungsbedarf minimal. Um den Jahreswechsel ( bzw.
bzw.  ) ist die Leistung der Solaranlage minimal und der Leistungsbedarf maximal.
a)(2)
) ist die Leistung der Solaranlage minimal und der Leistungsbedarf maximal.
a)(2)
 Zeitpunkt maximaler Leistung der Solaranlage und Maximalwert bestimmen
Um die maximale Leistung der Solaranlage und den Maximalwert zu bestimmen, kannst du den Graphen von
Zeitpunkt maximaler Leistung der Solaranlage und Maximalwert bestimmen
Um die maximale Leistung der Solaranlage und den Maximalwert zu bestimmen, kannst du den Graphen von  auf Hochpunkte per Hand oder mit deinem GTR untersuchen. Um einen Hochpunkt per Hand zu bestimmen, musst du Folgendes überprüfen:
auf Hochpunkte per Hand oder mit deinem GTR untersuchen. Um einen Hochpunkt per Hand zu bestimmen, musst du Folgendes überprüfen:
 einsetzt.
einsetzt.
 Lösungsweg A: Lösen per Hand
1. Schritt: 1. und 2. Ableitung von
Lösungsweg A: Lösen per Hand
1. Schritt: 1. und 2. Ableitung von  ermitteln
Das Polyom
ermitteln
Das Polyom  ist in der Aufgabenstellung gegeben. Daraus folgt für
ist in der Aufgabenstellung gegeben. Daraus folgt für  und
und  :
:

 2. Schritt: Notwendige Bedingung anwenden
Setze den Funktionsterm der
2. Schritt: Notwendige Bedingung anwenden
Setze den Funktionsterm der  Ableitung
Ableitung  gleich Null, um mögliche Nullstellen zu bestimmen:
$\begin{array}[t]{rll} f‘(t)\stackrel{!}=&0 & \scriptsize \mid\; \text{Funktionsterm von
gleich Null, um mögliche Nullstellen zu bestimmen:
$\begin{array}[t]{rll} f‘(t)\stackrel{!}=&0 & \scriptsize \mid\; \text{Funktionsterm von  einsetzen} \\[5pt] 4 \cdot t^3 - 72 \cdot t^2 +288 \cdot t=&0& \scriptsize \mid\; t \text{ ausklammern} \\[5pt] t \cdot ( 4 \cdot t^2 - 72 \cdot t +288)=&0 \end{array}$
Der Satz vom Nullprodukt liefert dir nun, dass das Produkt genau dann gleich Null ist, wenn einer der beiden Faktoren gleich Null ist. Damit hast du die erste Nullstelle
einsetzen} \\[5pt] 4 \cdot t^3 - 72 \cdot t^2 +288 \cdot t=&0& \scriptsize \mid\; t \text{ ausklammern} \\[5pt] t \cdot ( 4 \cdot t^2 - 72 \cdot t +288)=&0 \end{array}$
Der Satz vom Nullprodukt liefert dir nun, dass das Produkt genau dann gleich Null ist, wenn einer der beiden Faktoren gleich Null ist. Damit hast du die erste Nullstelle  bereits ermittelt. Betrachte nun den zweiten Faktor:
bereits ermittelt. Betrachte nun den zweiten Faktor:
![\(\begin{array}[t]{rll}
( 4 \cdot t^2 - 72 \cdot t +288)\stackrel{!}=&0 & \scriptsize \mid\; :4
\\[5pt]
t^2 - 18 \cdot t +72=&0
\end{array}\)](https://mathjax.schullv.de/48df86bf462208d531f178fb7b83ed977f05e29a6e8fab22fffe1ce1c91cbec4?color=5a5a5a) Du suchst nun die Nullstellen eines Polynoms
Du suchst nun die Nullstellen eines Polynoms  Grades. Dazu kannst du die PQ-Formel oder die Mitternachtsformel verwenden.
Grades. Dazu kannst du die PQ-Formel oder die Mitternachtsformel verwenden.
 Lösungsweg A: PQ-Formel
Mit
Lösungsweg A: PQ-Formel
Mit  und
und  hat dein Polynom die Form
hat dein Polynom die Form  . Also folgt für die Nullstellen:
. Also folgt für die Nullstellen:
![\(\begin{array}[t]{rll}
t_{2,3} =& - \dfrac{p}{2} \pm \sqrt {\left( {\frac{p}{2}} \right)^2 - q}
& \scriptsize \mid\; p \text{ und } q \text{ einsetzen}
\\[5pt]
t_{2,3} =& - \dfrac{-18}{2} \pm \sqrt {\left( {\frac{-18}{2}} \right)^2 - 72}
\\[5pt]
t_{2,3} =& 9 \pm \sqrt { 81 - 72}
\\[5pt]
t_{2,3} =& 9 \pm 3
\end{array}\)](https://mathjax.schullv.de/f9a8bea1ba268721e88a5e0735f3727201a0e949af33b0d30df21171d25484ca?color=5a5a5a) Damit erhältst du die weiteren Nullstellen
Damit erhältst du die weiteren Nullstellen  und
und  .
.
 Lösungsweg B: Mitternachtsformel
Du kannst die Mitternachtsformel hier direkt anwenden, wobei
Lösungsweg B: Mitternachtsformel
Du kannst die Mitternachtsformel hier direkt anwenden, wobei  ,
,  und
und  :
:
![\(\begin{array}[t]{rll}
t_{2,3} =& \dfrac{{ - (-72) \pm \sqrt {(-72)^2 - 4 \cdot 4 \cdot 288} }}{{2\cdot 4}}\\[5pt]
t_{2,3} =&\dfrac{{ 72 \pm \sqrt {5.184 - 4.608} }}{{8}}\\[5pt]
t_{2,3} =&9 \pm \dfrac{\sqrt{576}}{8} \\[5pt]
t_{2,3} =&9 \pm \dfrac{24}{8} \\[5pt]
t_{2,3} =& 9 \pm 3
\end{array}\)](https://mathjax.schullv.de/37cee6cb47d6f1083b3a660f8e223a26aaf0b650d117686af41b33976da8bffa?color=5a5a5a) Damit erhältst du die weiteren Nullstellen
Damit erhältst du die weiteren Nullstellen  und
und  .
3. Schritt: Hinreichende Bedingung überprüfen
Überprüfe nun das Vorzeichen von
.
3. Schritt: Hinreichende Bedingung überprüfen
Überprüfe nun das Vorzeichen von  an den gefundenen Nullstellen
an den gefundenen Nullstellen  und
und  . Daraus kannst du die Art der Extremstelle folgern.
. Daraus kannst du die Art der Extremstelle folgern.


 Also besitzt die Funktion
Also besitzt die Funktion  an der Stelle
an der Stelle  ein Maximum. Um die vollständigen Koordinaten des Hochpunkts
ein Maximum. Um die vollständigen Koordinaten des Hochpunkts  zu bestimmen, setzt du
zu bestimmen, setzt du  in
in  ein:
ein:
 4. Schritt: Randwerte überprüfen
Einsetzen der Randstellen
4. Schritt: Randwerte überprüfen
Einsetzen der Randstellen  und
und  ergibt:
ergibt:

 Damit besitzt der Graph von
Damit besitzt der Graph von  einen Hochpunkt mit den Koordinaten
einen Hochpunkt mit den Koordinaten  .
.
 (im Monat Juni) ist der Zeitpunkt der maximalen Leistung der Solaranlage und
(im Monat Juni) ist der Zeitpunkt der maximalen Leistung der Solaranlage und  der Maximalwert (in
der Maximalwert (in  ).
).
 Lösungsweg B: Lösen mit dem GTR
Wechsle mit deinem GTR in das GRAPH-Menü und speichere dort den Funktionsterm von
Lösungsweg B: Lösen mit dem GTR
Wechsle mit deinem GTR in das GRAPH-Menü und speichere dort den Funktionsterm von  . Hast du diesen dort eingegeben, dann stelle das Fenster so ein, dass du den gewünschten Bereich sehen kannst.
Wähle dann unter
. Hast du diesen dort eingegeben, dann stelle das Fenster so ein, dass du den gewünschten Bereich sehen kannst.
Wähle dann unter
 und
und  ein.
ein.
_2015_a2_loesung_a2_ti_nspire.png) Damit ist
Damit ist  (im Monat Juni) der Zeitpunkt der maximalen Leistung der Solaranlage und
(im Monat Juni) der Zeitpunkt der maximalen Leistung der Solaranlage und  der Maximalwert (in
der Maximalwert (in  ).
a)(3)
).
a)(3)
 Zeitpunkt der größten Abnahme des Leistungsbedarfs ermitteln
Gesucht ist der Zeitpunkt im Intervall
Zeitpunkt der größten Abnahme des Leistungsbedarfs ermitteln
Gesucht ist der Zeitpunkt im Intervall ![\([0;12]\)](https://mathjax.schullv.de/5ba9b38204a320e9433651393178f89e741e0a72de8e09a0201574090d0733c6?color=5a5a5a) , zu dem der durch
, zu dem der durch  beschriebene Leistungsbedarf am stärksten abnimmt. Die Änderungsrate
beschriebene Leistungsbedarf am stärksten abnimmt. Die Änderungsrate  beschreibt die Zu- oder Abnahme des Leistungsbedarf der Familie. Da der Zeitpunkt der stärksten Abnahme gesucht ist, erhältst du diesen durch das Bestimmen des Minimums der Änderungsrate
beschreibt die Zu- oder Abnahme des Leistungsbedarf der Familie. Da der Zeitpunkt der stärksten Abnahme gesucht ist, erhältst du diesen durch das Bestimmen des Minimums der Änderungsrate  . Dieses muss negativ sein, damit es sich um eine Abnahme handelt. Leite also
. Dieses muss negativ sein, damit es sich um eine Abnahme handelt. Leite also  ab und bestimme anschließend die Minimalstelle der Ableitung. Um eine Minimalstelle zu bestimmen, musst du Folgendes überprüfen:
ab und bestimme anschließend die Minimalstelle der Ableitung. Um eine Minimalstelle zu bestimmen, musst du Folgendes überprüfen:
 einsetzt.
einsetzt.
 Lösungsweg A: Lösen per Hand
1. Schritt:
Lösungsweg A: Lösen per Hand
1. Schritt:  ,
,  und
und  Ableitung von
Ableitung von  ermitteln
Das Polynom
ermitteln
Das Polynom  ist in der Aufgabenstellung gegeben. Damit folgt für die
ist in der Aufgabenstellung gegeben. Damit folgt für die  ,
,  und
und  Ableitung von
Ableitung von  :
:
![\(\begin{array}[t]{rll}
g(t)&=-t^4 + 26 \cdot t^3 - 167,5 \cdot t^2 -12,5 \cdot t + 2.053\\[10pt]
g‘(t)&=-\left(4\cdot t^3\right) + 26 \cdot \left(3 \cdot t^2\right) -167,5 \cdot \left(2 \cdot t\right) - 12,5\\[5pt]
&=-4\cdot t^3 + 78\cdot t^2 -335 \cdot t -12,5 \\[10pt]
g‘‘(t)&=-4\cdot \left(3\cdot t^2\right) + 78 \cdot \left(2\cdot t\right) - 335 \\[5pt]
&=-12 \cdot t^2 + 156 \cdot t -335 \\[10pt]
g‘‘‘(t)&=-12\cdot \left(2\cdot t\right) + 156 \\[5pt]
&=-24 \cdot t + 156
\end{array}\)](https://mathjax.schullv.de/4c6d6aefe249d3f3b46df1735b563c28e137c38c9f3cb4682f7eea596c8204eb?color=5a5a5a) 2. Schritt: Notwendige Bedingung anwenden
Da du das Minimum der Änderungsrate
2. Schritt: Notwendige Bedingung anwenden
Da du das Minimum der Änderungsrate  suchst, setzt du den Funktionsterm der
suchst, setzt du den Funktionsterm der  Ableitung
Ableitung  gleich Null, um mögliche Nullstellen zu bestimmen:
$\begin{array}[t]{rll} g‘‘(t)\stackrel{!}=&0 & \scriptsize \mid\; \text{Funktionsterm von
gleich Null, um mögliche Nullstellen zu bestimmen:
$\begin{array}[t]{rll} g‘‘(t)\stackrel{!}=&0 & \scriptsize \mid\; \text{Funktionsterm von  einsetzen} \\[5pt] - 12 \cdot t^2 + 156 \cdot t -335=&0& \scriptsize \mid\; :(-12) \\[5pt] t^2 - 13 \cdot t +\dfrac{335}{12}=&0 \end{array}$
Du suchst nun die Nullstellen eines Polynoms
einsetzen} \\[5pt] - 12 \cdot t^2 + 156 \cdot t -335=&0& \scriptsize \mid\; :(-12) \\[5pt] t^2 - 13 \cdot t +\dfrac{335}{12}=&0 \end{array}$
Du suchst nun die Nullstellen eines Polynoms  Grades. Dazu kannst du die PQ-Formel oder die Mitternachtsformel verwenden.
Grades. Dazu kannst du die PQ-Formel oder die Mitternachtsformel verwenden.
 Lösungsweg A: PQ-Formel
Mit
Lösungsweg A: PQ-Formel
Mit  und
und  hat dein Polynom die Form
hat dein Polynom die Form  . Also folgt für die Nullstellen:
. Also folgt für die Nullstellen:
![\(\begin{array}[t]{rll}
t_{1,2} =& - \dfrac{p}{2} \pm \sqrt {\left( {\frac{p}{2}} \right)^2 - q}
& \scriptsize \mid\; p \text{ und } q \text{ einsetzen}
\\[5pt]
t_{1,2} =& - \dfrac{-13}{2} \pm \sqrt {\left( {\dfrac{-13}{2}} \right)^2 -\dfrac{335}{12}}
\\[5pt]
t_{1,2} =& \dfrac{13}{2} \pm \sqrt { {\dfrac{169}{4}} -\dfrac{335}{12}}
\\[5pt]
t_{1,2} =& \dfrac{13}{2} \pm \sqrt { \dfrac{172}{12}}
\\[5pt]
t_{1,2} =& \dfrac{13}{2} \pm \sqrt { \dfrac{43}{3}}
\end{array}\)](https://mathjax.schullv.de/6d62eec857b216b93670b77704fdf24da3903ec2caeb7b9a4d77b2b1fe0aaa02?color=5a5a5a) Damit erhältst du die Nullstellen
Damit erhältst du die Nullstellen  und
und  .
.
 Lösungsweg B: Mitternachtsformel
Du kannst die Mitternachtsformel hier direkt anwenden, wobei
Lösungsweg B: Mitternachtsformel
Du kannst die Mitternachtsformel hier direkt anwenden, wobei  ,
,  und
und  :
:
![\(\begin{array}[t]{rll}
t_{1,2} =& \dfrac{{ - 156 \pm \sqrt {156^2 - 4 \cdot (-12) \cdot (-335)} }}{{2\cdot (-12)}}\\[5pt]
t_{1,2} =&\dfrac{{ 156 \pm \sqrt {24.336 - 16.080} }}{{24}}\\[5pt]
t_{1,2} =& \dfrac{13}{2} \pm \dfrac{\sqrt{8.256}}{24} \\[5pt]
t_{1,2} =& 6,5 \pm 3,79
\end{array}\)](https://mathjax.schullv.de/f485facef363dedddff554ae11d6b1fde8e71c81fc68de86f0a080318f34db8a?color=5a5a5a) Damit erhältst du die Nullstellen
Damit erhältst du die Nullstellen  und
und  .
3. Schritt: Hinreichende Bedingung überprüfen
Überprüfe nun das Vorzeichen von
.
3. Schritt: Hinreichende Bedingung überprüfen
Überprüfe nun das Vorzeichen von  an den gefundenen Nullstellen
an den gefundenen Nullstellen  und
und  . Daraus kannst du die Art der Extremstelle folgern.
. Daraus kannst du die Art der Extremstelle folgern.

 Also besitzt die Funktion
Also besitzt die Funktion  an der Stelle
an der Stelle  ein Minimum.
4. Schritt: Randwerte überprüfen
Einsetzen der Minimalstelle
ein Minimum.
4. Schritt: Randwerte überprüfen
Einsetzen der Minimalstelle  und der Randstellen
und der Randstellen  und
und  in
in  ergibt:
ergibt:


 Somit ist
Somit ist  der Zeitpunkt im Intervall
der Zeitpunkt im Intervall ![\([0;12]\)](https://mathjax.schullv.de/5ba9b38204a320e9433651393178f89e741e0a72de8e09a0201574090d0733c6?color=5a5a5a) , an dem der Leistungsbedarf der Familie innerhalb dieses Kalenderjahres am stärksten abnimmt.
, an dem der Leistungsbedarf der Familie innerhalb dieses Kalenderjahres am stärksten abnimmt.
 Lösungsweg B: Lösen mit dem GTR
Berechne wie im Lösungsweg A die erste Ableitung
Lösungsweg B: Lösen mit dem GTR
Berechne wie im Lösungsweg A die erste Ableitung  . Wechsle anschließend mit deinem GTR in das GRAPH-Menü und speichere dort den Funktionsterm von
. Wechsle anschließend mit deinem GTR in das GRAPH-Menü und speichere dort den Funktionsterm von  . Hast du diesen dort eingegeben, dann stelle das Fenster so ein, dass der gewünschte Bereich sichtbar ist.
Wähle dann unter
. Hast du diesen dort eingegeben, dann stelle das Fenster so ein, dass der gewünschte Bereich sichtbar ist.
Wähle dann unter
 und
und  ein.
ein.
_2015_a2_loesung_a3_ti_nspire.png) Also besitzt die Funktion
Also besitzt die Funktion  an der Stelle
an der Stelle  ein Minimum. Somit ist
ein Minimum. Somit ist  der Zeitpunkt im Intervall
der Zeitpunkt im Intervall ![\([0;12]\)](https://mathjax.schullv.de/5ba9b38204a320e9433651393178f89e741e0a72de8e09a0201574090d0733c6?color=5a5a5a) , an dem der Leistungsbedarf der Familie innerhalb dieses Kalenderjahres am stärksten abnimmt.
, an dem der Leistungsbedarf der Familie innerhalb dieses Kalenderjahres am stärksten abnimmt.
- Notwendige Bedingung:
- Hinreichende Bedingung:
6: Graph analysieren  3: Maximum
3: Maximum
den Befehl zum Bestimmen des Maximums aus und bestätige mit Enter. Gib anschließend deine Intervallgrenzen _2015_a2_loesung_a2_ti_nspire.png)
- Notwendige Bedingung:
- Hinreichende Bedingung:
6: Graph analysieren  2: Minimum
2: Minimum
den Befehl zum Bestimmen des Minimums aus und bestätige mit Enter. Gib anschließend deine Intervallgrenzen _2015_a2_loesung_a3_ti_nspire.png)
b)(1)
 Energiebedarf der Familie für das Kalenderjahr berechnen
Der Aufgabenstellung kannst du entnehmen, dass durch das Integral
Energiebedarf der Familie für das Kalenderjahr berechnen
Der Aufgabenstellung kannst du entnehmen, dass durch das Integral  der Energiebedarf der Familie im Zeitintervall
der Energiebedarf der Familie im Zeitintervall ![\([a;b]\)](https://mathjax.schullv.de/e84e12d6ffce2d83a82ceef8cfb5eb14688a4f4cce00a0d08d5357e2c6858142?color=5a5a5a) gegeben ist. Um den Energiebedarf für das Kalenderjahr zu berechnen, berechnest du das Integral mit den Grenzen
gegeben ist. Um den Energiebedarf für das Kalenderjahr zu berechnen, berechnest du das Integral mit den Grenzen  und
und  . Nutze dazu den Hauptsatz der Integralrechnung.
Setze die Grenzen in das Integral ein und berechne:
. Nutze dazu den Hauptsatz der Integralrechnung.
Setze die Grenzen in das Integral ein und berechne:
![\(\begin{array}[t]{rll}
\displaystyle\int_{0}^{12} g(t)\;\mathrm dt=&\displaystyle\int_{0}^{12} -t^4 + 26 \cdot t^3 -167,5 \cdot t^2 -12,5 \cdot t +2.053 \;\mathrm dt
\\[5pt]
=& \left[ - \dfrac{1}{5} \cdot t^5 + \dfrac{13}{2} \cdot t^4 -\dfrac{335}{6} \cdot t^3 -6,25 \cdot t^2 +2.053 \cdot t \right]_0^{12}
\\[5pt]
=&- \dfrac{1}{5} \cdot 12^5 + \dfrac{13}{2} \cdot 12^4 -\dfrac{335}{6} \cdot 12^3 -6,25 \cdot 12^2 +2.053 \cdot 12
\\[5pt]
=&-49.766,4 + 134.784 - 96.480 - 900 + 24.636
\\[5pt]
=& 12.273,6
\end{array}\)](https://mathjax.schullv.de/7c105122c81a23e288a2496d0b0590df4efda26434904bea11319f33aac75c00?color=5a5a5a) Also beträgt der Energiebedarf der Familie für das Kalenderjahr
Also beträgt der Energiebedarf der Familie für das Kalenderjahr  .
b)(2)
.
b)(2)
 Berechnen der Energie, die zum Heizen des Pools zur Verfügung steht
Der Pool wird mit der Energie geheizt, welche den Bedarf der Familie übersteigt. Diese Energie ist gerade die Differenz zwischen der von der Solaranlage erzeugten Energie und dem Energiebedarf der Familie. Zum Zeitpunkt
Berechnen der Energie, die zum Heizen des Pools zur Verfügung steht
Der Pool wird mit der Energie geheizt, welche den Bedarf der Familie übersteigt. Diese Energie ist gerade die Differenz zwischen der von der Solaranlage erzeugten Energie und dem Energiebedarf der Familie. Zum Zeitpunkt  ist diese Leistung somit durch
ist diese Leistung somit durch  gegeben. Für die überschüssige Energie im Intervall
gegeben. Für die überschüssige Energie im Intervall ![\(\left[3;9,5\right]\)](https://mathjax.schullv.de/a03ac5fe1f2ee83bfa4590b6a6c79fbf40a569515ebcc534bfeed1e72a1f310a?color=5a5a5a) berechne das Integral
berechne das Integral  . Berechne also zuerst
. Berechne also zuerst  . Danach kannst du per Hand oder mit deinem GTR weitermachen.
1. Schritt:
. Danach kannst du per Hand oder mit deinem GTR weitermachen.
1. Schritt:  berechnen
berechnen
![\(\begin{array}[t]{rll}
f(t)-g(t)&= \left(t^4-24 \cdot t^3 + 144 \cdot t^2 +400\right)-\left(-t^4 + 26 \cdot t^3 - 167,5 \cdot t^2 -12,5 \cdot t + 2.053\right) \\[5pt]
&=2\cdot t^4 - 50 \cdot t^3 + 311,5 \cdot t^2 +12,5 \cdot t -1.653
\end{array}\)](https://mathjax.schullv.de/f6eac637f555ff38ea83de9c273e93aba9395023388b03e70f09c825d19bf453?color=5a5a5a)
 Lösungsweg A: Per Hand
Bestimme nun eine Stammfunktion
Lösungsweg A: Per Hand
Bestimme nun eine Stammfunktion  und berechne damit das Integral
und berechne damit das Integral  .
2. Schritt: Stammfunktion
.
2. Schritt: Stammfunktion  bestimmen
bestimmen
![\(\begin{array}[t]{rll}
\displaystyle\int_{}^{} \left(f(t)-g(t)\right) \;\mathrm dt&=\displaystyle\int_{}^{}2\cdot t^4 - 50 \cdot t^3 + 311,5 \cdot t^2 +12,5 \cdot t -1.653 \;\mathrm dt\\[5pt]
&=\dfrac{1}{5}\cdot 2t^5-\dfrac{1}{4}\cdot 50t^4+ \dfrac{1}{3}\cdot 311,5t^3+\dfrac{1}{2}\cdot12,5t^2-1.653 t +c\\[5pt]
&=\dfrac{2}{5}t^5-\dfrac{25}{2}t^4+ \dfrac{623}{6}t^3 +\dfrac{25}{4}t^2-1.653 t +c
\end{array}\)](https://mathjax.schullv.de/254a2608a72d2a52686245f0652e715d8804574d5137d03f052bc76bb990cb20?color=5a5a5a) Wähle
Wähle  und damit ist
und damit ist  eine Stammfunktion von
eine Stammfunktion von  .
3. Schritt: Integral
.
3. Schritt: Integral  berechnen
berechnen
![\(\begin{array}[t]{rll}
\displaystyle\int_{3}^{9,5} \left(f(t)-g(t)\right) \;\mathrm dt&= (F-G)(9,5)-(F-G)(3)\\[5pt]
&=\left(\dfrac{2}{5}\cdot 9,5^5-\dfrac{25}{2}\cdot 9,5^4+ \dfrac{623}{6}\cdot 9,5^3+\dfrac{25}{4}\cdot 9,5^2-1.653 \cdot 9,5\right) \\[5pt]
&- \left(\dfrac{2}{5}\cdot 3^5-\dfrac{25}{2}\cdot 3^4+ \dfrac{623}{6}\cdot 3^3+\dfrac{25}{4}\cdot 3^2-1.653 \cdot 3\right)\\[5pt]
&= 3.022,62 - \left(-3014,55\right)\\[5pt]
&= 3.022,62 + 3014,55\\[5pt]
&= 6.037,173
\end{array}\)](https://mathjax.schullv.de/db79153c98144fa0d21114682e3004121eaf5e625746058eee33531f2ec70e75?color=5a5a5a) Der Familie stehen somit
Der Familie stehen somit  kWh Energie zum Heizen des Pools zur Verfügung.
kWh Energie zum Heizen des Pools zur Verfügung.
 Lösungsweg B: Lösen mit dem GTR
Wechsle mit deinem GTR in das GRAPH-Menü und speichere dort den Funktionsterm von
Lösungsweg B: Lösen mit dem GTR
Wechsle mit deinem GTR in das GRAPH-Menü und speichere dort den Funktionsterm von  . Hast du diesen dort eingegeben, dann stelle das Fenster so ein, dass der gewünschte Bereich sichtbar ist.
Bestimme dann über
. Hast du diesen dort eingegeben, dann stelle das Fenster so ein, dass der gewünschte Bereich sichtbar ist.
Bestimme dann über
 in den Grenzen des Intervalls
in den Grenzen des Intervalls ![\(\left[3;9,5\right]\)](https://mathjax.schullv.de/a03ac5fe1f2ee83bfa4590b6a6c79fbf40a569515ebcc534bfeed1e72a1f310a?color=5a5a5a) .
.
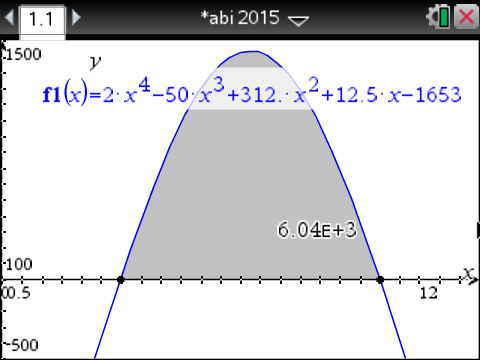 Der Familie stehen somit
Der Familie stehen somit  kWh Energie zum Heizen des Pools zur Verfügung.
kWh Energie zum Heizen des Pools zur Verfügung.
6: Graph analysieren  6: Integral
6: Integral
das Integral über 
c)(1)
 Zeigen, dass
Zeigen, dass  eine der Funktionen
eine der Funktionen  ist und zugehöriges
ist und zugehöriges  berechnen
Hier musst du ein
berechnen
Hier musst du ein ![\(a \in [0,5 1,5]\)](https://mathjax.schullv.de/b56df50ba3a9c59c14365fa29be93a514101a315c7da4bf0b8981756721496c0?color=5a5a5a) finden, sodass
finden, sodass  gilt. Schaue dir dazu die beiden Funktionsgleichungen an und leite anhand des Koeffizienten des Terms mit der höchsten Ordnung ein
gilt. Schaue dir dazu die beiden Funktionsgleichungen an und leite anhand des Koeffizienten des Terms mit der höchsten Ordnung ein  her, für das du die Behauptung überprüfst und das zugehörige
her, für das du die Behauptung überprüfst und das zugehörige  berechnest.
Da
berechnest.
Da  der Term der höchsten Ordnung von
der Term der höchsten Ordnung von  und
und  ist, wähle
ist, wähle  so, dass diese dieselben Koeffizienten besitzen, also
so, dass diese dieselben Koeffizienten besitzen, also  . Damit gilt:
. Damit gilt:
 Somit hast du die Behauptung nachgewiesen. Berechne nun das zugehörige
Somit hast du die Behauptung nachgewiesen. Berechne nun das zugehörige  :
:
![\(\begin{array}[t]{rll}
w=& 116 - 66 \cdot a & \scriptsize \mid\; a=1 \text{ einsetzen}
\\[5pt]
=& 116 - 66
\\[5pt]
=& 50
\end{array}\)](https://mathjax.schullv.de/6da9b39b204a7256db09b3d6b4313d2de40dc16b3ea036bef46aa16452195380?color=5a5a5a) Also beträgt der zugehörige Neigungswinkel
Also beträgt der zugehörige Neigungswinkel  .
c)(2)
.
c)(2)
 Maximale in einem Jahr aus der Solaranlage abrufbare Energie für
Maximale in einem Jahr aus der Solaranlage abrufbare Energie für  nachweisen
Berechne zunächst die für ein beliebiges
nachweisen
Berechne zunächst die für ein beliebiges  innerhalb eines Jahres abrufbare Energie durch das Integral
innerhalb eines Jahres abrufbare Energie durch das Integral  . Ermittle für die erhaltene, von
. Ermittle für die erhaltene, von  abhängige Funktion das Maximum über
abhängige Funktion das Maximum über  . Erhältst du daraus
. Erhältst du daraus  , hast du die Behauptung nachgewiesen.
1. Schritt: Integral
, hast du die Behauptung nachgewiesen.
1. Schritt: Integral  berechnen
Mit dem Hauptsatz der Integralrechnung ergibt sich:
berechnen
Mit dem Hauptsatz der Integralrechnung ergibt sich:
![\(\begin{array}[t]{rll}
\displaystyle\int_0^{12} f_a(t) \;\mathrm dt=& \displaystyle\int_0^{12} a \cdot \left(t^4-24 \cdot t^3 + 144 \cdot t^2 +400\right) - 400 \cdot \left(a^2 -1 \right) \;\mathrm dt
\\[5pt]
=&\left[a \cdot \left(\dfrac{1}{5} \cdot t^5 - 6 \cdot t^4 + 48 \cdot t^3 +400 \cdot t \right) - 400 \cdot \left(a^2 -1 \right) \cdot t \right]_0^{12}
\\[5pt]
=&a \cdot \left(\dfrac{1}{5} \cdot 12^5 - 6 \cdot 12^4 + 48 \cdot 12^3 +400 \cdot 12 \right) - 400 \cdot \left(a^2 -1 \right) \cdot 12
\\[5pt]
=& a \cdot \left( \dfrac{65.472}{5}\right) - 4.800 \cdot \left(a^2 -1 \right)
\\[5pt]
=&:E(a)
\end{array}\)](https://mathjax.schullv.de/df431607d71ee5e24e56ea62163aeeb7c54713e0b77980cc3ace6fecd39b19f9?color=5a5a5a) Die Funktion
Die Funktion  gibt dir nun die in einem Jahr aus der Solaranlage abrufbare Energie in Abhängigkeit von
gibt dir nun die in einem Jahr aus der Solaranlage abrufbare Energie in Abhängigkeit von  an. Ermittle also das Maximum von
an. Ermittle also das Maximum von  . Dies kannst du per Hand oder mit deinem GTR erledigen.
2. Schritt: Maximum von
. Dies kannst du per Hand oder mit deinem GTR erledigen.
2. Schritt: Maximum von  bestimmen
bestimmen
 Lösungsweg A: Per Hand
Bestimme das Maximum von
Lösungsweg A: Per Hand
Bestimme das Maximum von  , indem du zunächst die notwendige Bedingung anwendest. Bei der Funktion
, indem du zunächst die notwendige Bedingung anwendest. Bei der Funktion  handelt es sich um eine nach unten geöffnete Parabel. Somit fällt die Überprüfung der hinreichenden Bedingung weg und auch die Überprüfung der Randwerte ist hinfällig.
handelt es sich um eine nach unten geöffnete Parabel. Somit fällt die Überprüfung der hinreichenden Bedingung weg und auch die Überprüfung der Randwerte ist hinfällig.

 Ableitung von
Ableitung von  ermitteln
Leite
ermitteln
Leite  nach
nach  ab:
ab:

 Notwendige Bedingung anwenden
Setze den Funktionsterm der
Notwendige Bedingung anwenden
Setze den Funktionsterm der  Ableitung
Ableitung  gleich Null, um mögliche Nullstellen zu bestimmen:
gleich Null, um mögliche Nullstellen zu bestimmen:
![\(\begin{array}[t]{rll}
E‘(a)\stackrel{!}=&0&\scriptsize \mid\; E‘(a) \text{ einsetzen}
\\[5pt]
\dfrac{65.472}{5} - 9.600 \cdot a =&0&\scriptsize \mid\; +9.600 \cdot a
\\[5pt]
\dfrac{65.472}{5}=&9.600 \cdot a &\scriptsize \mid\; :9.600
\\[5pt]
\dfrac{341}{250}=&a
\\[5pt]
1,364=&a
\end{array}\)](https://mathjax.schullv.de/a3e46c7e5db14a8029404d4b26bb9bbc5acf5c667c206560e77ce23a671c9cde?color=5a5a5a) Damit kommt nur
Damit kommt nur  als Maximum in Frage. Aufgrund der Parabelform von
als Maximum in Frage. Aufgrund der Parabelform von  besitzt die Funktion an der Stelle
besitzt die Funktion an der Stelle  eine Maximalstelle.
Damit hast du nachgewiesen, dass die in einem Jahr aus der Solaranlage abrufbare Energie für
eine Maximalstelle.
Damit hast du nachgewiesen, dass die in einem Jahr aus der Solaranlage abrufbare Energie für 
 am größten ist.
am größten ist.
 Lösungsweg B: Lösen mit dem GTR
Wechsle mit deinem GTR in das GRAPH-Menü und speichere dort den Funktionsterm von
Lösungsweg B: Lösen mit dem GTR
Wechsle mit deinem GTR in das GRAPH-Menü und speichere dort den Funktionsterm von  . Hast du diesen dort eingegeben, dann stelle das Fenster so ein, dass du den gewünschten Bereich sehen kannst.
Wähle dann unter
. Hast du diesen dort eingegeben, dann stelle das Fenster so ein, dass du den gewünschten Bereich sehen kannst.
Wähle dann unter
 und
und  ein.
ein.
_2015_a2_loesung_c2_ti_nspire.png) Damit hast du nachgewiesen, dass die in einem Jahr aus der Solaranlage abrufbare Energie für
Damit hast du nachgewiesen, dass die in einem Jahr aus der Solaranlage abrufbare Energie für 
 am größten ist.
c)(3)
am größten ist.
c)(3)
 Behauptung des Solaranlagenherstellers begründen
Abbildung 2 liefert dir den Graphen
Behauptung des Solaranlagenherstellers begründen
Abbildung 2 liefert dir den Graphen  für den Neigungswinkel
für den Neigungswinkel  und den Graphen
und den Graphen  für
für  . Die von der Solaranlage mit dem entsprechenden Neigungswinkel bereitgestellte Energie wird durch die Flächen unterhalb der entsprechenden Graphen dargestellt. Zudem ist der Energiebedarf der Familie durch die Fläche unterhalb des Graphen der Funktion
. Die von der Solaranlage mit dem entsprechenden Neigungswinkel bereitgestellte Energie wird durch die Flächen unterhalb der entsprechenden Graphen dargestellt. Zudem ist der Energiebedarf der Familie durch die Fläche unterhalb des Graphen der Funktion  dargestellt.
Nun erkennst du anhand der Abbildung 2, dass die Fläche unterhalb des Graphen von
dargestellt.
Nun erkennst du anhand der Abbildung 2, dass die Fläche unterhalb des Graphen von  einen größeren Anteil an der Fläche unterhalb von
einen größeren Anteil an der Fläche unterhalb von  überdeckt als die Fläche unterhalb von
überdeckt als die Fläche unterhalb von  .
Damit deckt über das ganze Kalenderjahr die Solaranlage mit Neigungswinkel
.
Damit deckt über das ganze Kalenderjahr die Solaranlage mit Neigungswinkel  einen höheren Anteil am Leistungsbedarf der Familie als die Solaranlage mit Neigungswinkel
einen höheren Anteil am Leistungsbedarf der Familie als die Solaranlage mit Neigungswinkel  .
.
6: Graph analysieren  3: Maximum
3: Maximum
den Befehl zum Bestimmen des Maximums aus und bestätige mit Enter. Gib anschließend deine Intervallgrenzen _2015_a2_loesung_c2_ti_nspire.png)
a)(1)
 Graphen von
Graphen von  und
und  im Sachzusammenhang vergleichen
Hier sollst du die Graphen von
im Sachzusammenhang vergleichen
Hier sollst du die Graphen von  und
und  im Sachzusammenhang vergleichen. Die Funktion
im Sachzusammenhang vergleichen. Die Funktion  modelliert die Leistung der Solaranlage, die Funktion
modelliert die Leistung der Solaranlage, die Funktion  den Leistungsbedarf der Familie. Du erkennst, dass in den Intervallen
den Leistungsbedarf der Familie. Du erkennst, dass in den Intervallen ![\(\left[0;3\right]\)](https://mathjax.schullv.de/e6ac5d60749307c17b05c9a262850c1a1312bb0bdac1077886594150a0f01657?color=5a5a5a) und
und ![\(\left[9,5;12\right]\)](https://mathjax.schullv.de/47d231a407dc5122a8184c20a6aacccc109aaeff05e0642aed51402f3d886a66?color=5a5a5a) der Graph der Funktion
der Graph der Funktion  oberhalb des Graphen von
oberhalb des Graphen von  liegt, im Intervall
liegt, im Intervall ![\(\left[3;9,5\right]\)](https://mathjax.schullv.de/a03ac5fe1f2ee83bfa4590b6a6c79fbf40a569515ebcc534bfeed1e72a1f310a?color=5a5a5a) ist es gerade andersrum und der Graph von
ist es gerade andersrum und der Graph von  liegt über dem Graphen von
liegt über dem Graphen von  . Die Graphen von
. Die Graphen von  und
und  verhalten sich gegenläufig um einen Mittelwert von ca. 1.000.
Im Sachzusammenhang lässt sich dies so deuten, dass im Winter (Intervalle
verhalten sich gegenläufig um einen Mittelwert von ca. 1.000.
Im Sachzusammenhang lässt sich dies so deuten, dass im Winter (Intervalle ![\(\left[0;3\right]\)](https://mathjax.schullv.de/e6ac5d60749307c17b05c9a262850c1a1312bb0bdac1077886594150a0f01657?color=5a5a5a) und
und ![\(\left[9,5;12\right]\)](https://mathjax.schullv.de/47d231a407dc5122a8184c20a6aacccc109aaeff05e0642aed51402f3d886a66?color=5a5a5a) ) weniger Energie produziert wird als benötigt wird und die Solaranlage den Energiebedarf nicht vollständig deckt. Im Sommer (Intervall
) weniger Energie produziert wird als benötigt wird und die Solaranlage den Energiebedarf nicht vollständig deckt. Im Sommer (Intervall ![\(\left[3;9,5\right]\)](https://mathjax.schullv.de/a03ac5fe1f2ee83bfa4590b6a6c79fbf40a569515ebcc534bfeed1e72a1f310a?color=5a5a5a) ) wird mehr Energie als benötigt produziert und der Energiebedarf wird vollständig gedeckt.
Um den Juni (
) wird mehr Energie als benötigt produziert und der Energiebedarf wird vollständig gedeckt.
Um den Juni ( ) ist die Leistung der Solaranlage maximal und der Leistungsbedarf minimal. Um den Jahreswechsel (
) ist die Leistung der Solaranlage maximal und der Leistungsbedarf minimal. Um den Jahreswechsel ( bzw.
bzw.  ) ist die Leistung der Solaranlage minimal und der Leistungsbedarf maximal.
a)(2)
) ist die Leistung der Solaranlage minimal und der Leistungsbedarf maximal.
a)(2)
 Zeitpunkt maximaler Leistung der Solaranlage und Maximalwert bestimmen
Um die maximale Leistung der Solaranlage und den Maximalwert zu bestimmen, kannst du den Graphen von
Zeitpunkt maximaler Leistung der Solaranlage und Maximalwert bestimmen
Um die maximale Leistung der Solaranlage und den Maximalwert zu bestimmen, kannst du den Graphen von  auf Hochpunkte per Hand oder mit deinem GTR untersuchen. Um einen Hochpunkt per Hand zu bestimmen, musst du Folgendes überprüfen:
auf Hochpunkte per Hand oder mit deinem GTR untersuchen. Um einen Hochpunkt per Hand zu bestimmen, musst du Folgendes überprüfen:
 einsetzt.
einsetzt.
 Lösungsweg A: Lösen per Hand
1. Schritt: 1. und 2. Ableitung von
Lösungsweg A: Lösen per Hand
1. Schritt: 1. und 2. Ableitung von  ermitteln
Das Polyom
ermitteln
Das Polyom  ist in der Aufgabenstellung gegeben. Daraus folgt für
ist in der Aufgabenstellung gegeben. Daraus folgt für  und
und  :
:

 2. Schritt: Notwendige Bedingung anwenden
Setze den Funktionsterm der
2. Schritt: Notwendige Bedingung anwenden
Setze den Funktionsterm der  Ableitung
Ableitung  gleich Null, um mögliche Nullstellen zu bestimmen:
$\begin{array}[t]{rll} f‘(t)\stackrel{!}=&0 & \scriptsize \mid\; \text{Funktionsterm von
gleich Null, um mögliche Nullstellen zu bestimmen:
$\begin{array}[t]{rll} f‘(t)\stackrel{!}=&0 & \scriptsize \mid\; \text{Funktionsterm von  einsetzen} \\[5pt] 4 \cdot t^3 - 72 \cdot t^2 +288 \cdot t=&0& \scriptsize \mid\; t \text{ ausklammern} \\[5pt] t \cdot ( 4 \cdot t^2 - 72 \cdot t +288)=&0 \end{array}$
Der Satz vom Nullprodukt liefert dir nun, dass das Produkt genau dann gleich Null ist, wenn einer der beiden Faktoren gleich Null ist. Damit hast du die erste Nullstelle
einsetzen} \\[5pt] 4 \cdot t^3 - 72 \cdot t^2 +288 \cdot t=&0& \scriptsize \mid\; t \text{ ausklammern} \\[5pt] t \cdot ( 4 \cdot t^2 - 72 \cdot t +288)=&0 \end{array}$
Der Satz vom Nullprodukt liefert dir nun, dass das Produkt genau dann gleich Null ist, wenn einer der beiden Faktoren gleich Null ist. Damit hast du die erste Nullstelle  bereits ermittelt. Betrachte nun den zweiten Faktor:
bereits ermittelt. Betrachte nun den zweiten Faktor:
![\(\begin{array}[t]{rll}
( 4 \cdot t^2 - 72 \cdot t +288)\stackrel{!}=&0 & \scriptsize \mid\; :4
\\[5pt]
t^2 - 18 \cdot t +72=&0
\end{array}\)](https://mathjax.schullv.de/48df86bf462208d531f178fb7b83ed977f05e29a6e8fab22fffe1ce1c91cbec4?color=5a5a5a) Du suchst nun die Nullstellen eines Polynoms
Du suchst nun die Nullstellen eines Polynoms  Grades. Dazu kannst du die PQ-Formel oder die Mitternachtsformel verwenden.
Grades. Dazu kannst du die PQ-Formel oder die Mitternachtsformel verwenden.
 Lösungsweg A: PQ-Formel
Mit
Lösungsweg A: PQ-Formel
Mit  und
und  hat dein Polynom die Form
hat dein Polynom die Form  . Also folgt für die Nullstellen:
. Also folgt für die Nullstellen:
![\(\begin{array}[t]{rll}
t_{2,3} =& - \dfrac{p}{2} \pm \sqrt {\left( {\frac{p}{2}} \right)^2 - q}
& \scriptsize \mid\; p \text{ und } q \text{ einsetzen}
\\[5pt]
t_{2,3} =& - \dfrac{-18}{2} \pm \sqrt {\left( {\frac{-18}{2}} \right)^2 - 72}
\\[5pt]
t_{2,3} =& 9 \pm \sqrt { 81 - 72}
\\[5pt]
t_{2,3} =& 9 \pm 3
\end{array}\)](https://mathjax.schullv.de/f9a8bea1ba268721e88a5e0735f3727201a0e949af33b0d30df21171d25484ca?color=5a5a5a) Damit erhältst du die weiteren Nullstellen
Damit erhältst du die weiteren Nullstellen  und
und  .
.
 Lösungsweg B: Mitternachtsformel
Du kannst die Mitternachtsformel hier direkt anwenden, wobei
Lösungsweg B: Mitternachtsformel
Du kannst die Mitternachtsformel hier direkt anwenden, wobei  ,
,  und
und  :
:
![\(\begin{array}[t]{rll}
t_{2,3} =& \dfrac{{ - (-72) \pm \sqrt {(-72)^2 - 4 \cdot 4 \cdot 288} }}{{2\cdot 4}}\\[5pt]
t_{2,3} =&\dfrac{{ 72 \pm \sqrt {5.184 - 4.608} }}{{8}}\\[5pt]
t_{2,3} =&9 \pm \dfrac{\sqrt{576}}{8} \\[5pt]
t_{2,3} =&9 \pm \dfrac{24}{8} \\[5pt]
t_{2,3} =& 9 \pm 3
\end{array}\)](https://mathjax.schullv.de/37cee6cb47d6f1083b3a660f8e223a26aaf0b650d117686af41b33976da8bffa?color=5a5a5a) Damit erhältst du die weiteren Nullstellen
Damit erhältst du die weiteren Nullstellen  und
und  .
3. Schritt: Hinreichende Bedingung überprüfen
Überprüfe nun das Vorzeichen von
.
3. Schritt: Hinreichende Bedingung überprüfen
Überprüfe nun das Vorzeichen von  an den gefundenen Nullstellen
an den gefundenen Nullstellen  und
und  . Daraus kannst du die Art der Extremstelle folgern.
. Daraus kannst du die Art der Extremstelle folgern.


 Also besitzt die Funktion
Also besitzt die Funktion  an der Stelle
an der Stelle  ein Maximum. Um die vollständigen Koordinaten des Hochpunkts
ein Maximum. Um die vollständigen Koordinaten des Hochpunkts  zu bestimmen, setzt du
zu bestimmen, setzt du  in
in  ein:
ein:
 4. Schritt: Randwerte überprüfen
Einsetzen der Randstellen
4. Schritt: Randwerte überprüfen
Einsetzen der Randstellen  und
und  ergibt:
ergibt:

 Damit besitzt der Graph von
Damit besitzt der Graph von  einen Hochpunkt mit den Koordinaten
einen Hochpunkt mit den Koordinaten  .
.
 (im Monat Juni) ist der Zeitpunkt der maximalen Leistung der Solaranlage und
(im Monat Juni) ist der Zeitpunkt der maximalen Leistung der Solaranlage und  der Maximalwert (in
der Maximalwert (in  ).
).
 Lösungsweg B: Lösen mit dem GTR
Wechsle mit deinem GTR in den Graph-Modus und speichere dort den Funktionsterm von
Lösungsweg B: Lösen mit dem GTR
Wechsle mit deinem GTR in den Graph-Modus und speichere dort den Funktionsterm von  . Hast du diesen dort gespeichert, gib unter
. Hast du diesen dort gespeichert, gib unter
 und
und  ein. Wechsle wieder in das Y=-Menü und lass dir den zugehörigen Graph über DRAW anzeigen.
Wähle dann unter
ein. Wechsle wieder in das Y=-Menü und lass dir den zugehörigen Graph über DRAW anzeigen.
Wähle dann unter
_2015_a2_loesung_a2_casio.png) Damit ist
Damit ist  (im Monat Juni) der Zeitpunkt der maximalen Leistung der Solaranlage und
(im Monat Juni) der Zeitpunkt der maximalen Leistung der Solaranlage und  der Maximalwert (in
der Maximalwert (in  ).
a)(3)
).
a)(3)
 Zeitpunkt der größten Abnahme des Leistungsbedarfs ermitteln
Gesucht ist der Zeitpunkt im Intervall
Zeitpunkt der größten Abnahme des Leistungsbedarfs ermitteln
Gesucht ist der Zeitpunkt im Intervall ![\([0;12]\)](https://mathjax.schullv.de/5ba9b38204a320e9433651393178f89e741e0a72de8e09a0201574090d0733c6?color=5a5a5a) , zu dem der durch
, zu dem der durch  beschriebene Leistungsbedarf am stärksten abnimmt. Die Änderungsrate
beschriebene Leistungsbedarf am stärksten abnimmt. Die Änderungsrate  beschreibt die Zu- oder Abnahme des Leistungsbedarf der Familie. Da der Zeitpunkt der stärksten Abnahme gesucht ist, erhältst du diesen durch das Bestimmen des Minimums der Änderungsrate
beschreibt die Zu- oder Abnahme des Leistungsbedarf der Familie. Da der Zeitpunkt der stärksten Abnahme gesucht ist, erhältst du diesen durch das Bestimmen des Minimums der Änderungsrate  . Dieses muss negativ sein, damit es sich um eine Abnahme handelt. Leite also
. Dieses muss negativ sein, damit es sich um eine Abnahme handelt. Leite also  ab und bestimme anschließend die Minimalstelle der Ableitung. Um eine Minimalstelle zu bestimmen, musst du Folgendes überprüfen:
ab und bestimme anschließend die Minimalstelle der Ableitung. Um eine Minimalstelle zu bestimmen, musst du Folgendes überprüfen:
 einsetzt.
einsetzt.
 Lösungsweg A: Lösen per Hand
1. Schritt:
Lösungsweg A: Lösen per Hand
1. Schritt:  ,
,  und
und  Ableitung von
Ableitung von  ermitteln
Das Polynom
ermitteln
Das Polynom  ist in der Aufgabenstellung gegeben. Damit folgt für die
ist in der Aufgabenstellung gegeben. Damit folgt für die  ,
,  und
und  Ableitung von
Ableitung von  :
:
![\(\begin{array}[t]{rll}
g(t)&=-t^4 + 26 \cdot t^3 - 167,5 \cdot t^2 -12,5 \cdot t + 2.053\\[10pt]
g‘(t)&=-\left(4\cdot t^3\right) + 26 \cdot \left(3 \cdot t^2\right) -167,5 \cdot \left(2 \cdot t\right) - 12,5\\[5pt]
&=-4\cdot t^3 + 78\cdot t^2 -335 \cdot t -12,5 \\[10pt]
g‘‘(t)&=-4\cdot \left(3\cdot t^2\right) + 78 \cdot \left(2\cdot t\right) - 335 \\[5pt]
&=-12 \cdot t^2 + 156 \cdot t -335 \\[10pt]
g‘‘‘(t)&=-12\cdot \left(2\cdot t\right) + 156 \\[5pt]
&=-24 \cdot t + 156
\end{array}\)](https://mathjax.schullv.de/4c6d6aefe249d3f3b46df1735b563c28e137c38c9f3cb4682f7eea596c8204eb?color=5a5a5a) 2. Schritt: Notwendige Bedingung anwenden
Da du das Minimum der Änderungsrate
2. Schritt: Notwendige Bedingung anwenden
Da du das Minimum der Änderungsrate  suchst, setzt du den Funktionsterm der
suchst, setzt du den Funktionsterm der  Ableitung
Ableitung  gleich Null, um mögliche Nullstellen zu bestimmen:
$\begin{array}[t]{rll} g‘‘(t)\stackrel{!}=&0 & \scriptsize \mid\; \text{Funktionsterm von
gleich Null, um mögliche Nullstellen zu bestimmen:
$\begin{array}[t]{rll} g‘‘(t)\stackrel{!}=&0 & \scriptsize \mid\; \text{Funktionsterm von  einsetzen} \\[5pt] - 12 \cdot t^2 + 156 \cdot t -335=&0& \scriptsize \mid\; :(-12) \\[5pt] t^2 - 13 \cdot t +\dfrac{335}{12}=&0 \end{array}$
Du suchst nun die Nullstellen eines Polynoms
einsetzen} \\[5pt] - 12 \cdot t^2 + 156 \cdot t -335=&0& \scriptsize \mid\; :(-12) \\[5pt] t^2 - 13 \cdot t +\dfrac{335}{12}=&0 \end{array}$
Du suchst nun die Nullstellen eines Polynoms  Grades. Dazu kannst du die PQ-Formel oder die Mitternachtsformel verwenden.
Grades. Dazu kannst du die PQ-Formel oder die Mitternachtsformel verwenden.
 Lösungsweg A: PQ-Formel
Mit
Lösungsweg A: PQ-Formel
Mit  und
und  hat dein Polynom die Form
hat dein Polynom die Form  . Also folgt für die Nullstellen:
. Also folgt für die Nullstellen:
![\(\begin{array}[t]{rll}
t_{1,2} =& - \dfrac{p}{2} \pm \sqrt {\left( {\frac{p}{2}} \right)^2 - q}
& \scriptsize \mid\; p \text{ und } q \text{ einsetzen}
\\[5pt]
t_{1,2} =& - \dfrac{-13}{2} \pm \sqrt {\left( {\dfrac{-13}{2}} \right)^2 -\dfrac{335}{12}}
\\[5pt]
t_{1,2} =& \dfrac{13}{2} \pm \sqrt { {\dfrac{169}{4}} -\dfrac{335}{12}}
\\[5pt]
t_{1,2} =& \dfrac{13}{2} \pm \sqrt { \dfrac{172}{12}}
\\[5pt]
t_{1,2} =& \dfrac{13}{2} \pm \sqrt { \dfrac{43}{3}}
\end{array}\)](https://mathjax.schullv.de/6d62eec857b216b93670b77704fdf24da3903ec2caeb7b9a4d77b2b1fe0aaa02?color=5a5a5a) Damit erhältst du die Nullstellen
Damit erhältst du die Nullstellen  und
und  .
.
 Lösungsweg B: Mitternachtsformel
Du kannst die Mitternachtsformel hier direkt anwenden, wobei
Lösungsweg B: Mitternachtsformel
Du kannst die Mitternachtsformel hier direkt anwenden, wobei  ,
,  und
und  :
:
![\(\begin{array}[t]{rll}
t_{1,2} =& \dfrac{{ - 156 \pm \sqrt {156^2 - 4 \cdot (-12) \cdot (-335)} }}{{2\cdot (-12)}}\\[5pt]
t_{1,2} =&\dfrac{{ 156 \pm \sqrt {24.336 - 16.080} }}{{24}}\\[5pt]
t_{1,2} =& \dfrac{13}{2} \pm \dfrac{\sqrt{8.256}}{24} \\[5pt]
t_{1,2} =& 6,5 \pm 3,79
\end{array}\)](https://mathjax.schullv.de/f485facef363dedddff554ae11d6b1fde8e71c81fc68de86f0a080318f34db8a?color=5a5a5a) Damit erhältst du die Nullstellen
Damit erhältst du die Nullstellen  und
und  .
3. Schritt: Hinreichende Bedingung überprüfen
Überprüfe nun das Vorzeichen von
.
3. Schritt: Hinreichende Bedingung überprüfen
Überprüfe nun das Vorzeichen von  an den gefundenen Nullstellen
an den gefundenen Nullstellen  und
und  . Daraus kannst du die Art der Extremstelle folgern.
. Daraus kannst du die Art der Extremstelle folgern.

 Also besitzt die Funktion
Also besitzt die Funktion  an der Stelle
an der Stelle  ein Minimum.
4. Schritt: Randwerte überprüfen
Einsetzen der Randstellen der Minimalstelle
ein Minimum.
4. Schritt: Randwerte überprüfen
Einsetzen der Randstellen der Minimalstelle  und der Randstellen
und der Randstellen  und
und  in
in  ergibt:
ergibt:


 Somit ist
Somit ist  der Zeitpunkt im Intervall
der Zeitpunkt im Intervall ![\([0;12]\)](https://mathjax.schullv.de/5ba9b38204a320e9433651393178f89e741e0a72de8e09a0201574090d0733c6?color=5a5a5a) , an dem der Leistungsbedarf der Familie innerhalb dieses Kalenderjahres am stärksten abnimmt.
, an dem der Leistungsbedarf der Familie innerhalb dieses Kalenderjahres am stärksten abnimmt.
 Lösungsweg B: Lösen mit dem GTR
Berechne wie im Lösungsweg A die erste Ableitung
Lösungsweg B: Lösen mit dem GTR
Berechne wie im Lösungsweg A die erste Ableitung  . Wechsle anschließend mit deinem GTR in den Graph-Modus und speichere dort den Funktionsterm von
. Wechsle anschließend mit deinem GTR in den Graph-Modus und speichere dort den Funktionsterm von  . Hast du diesen dort gespeichert, gib unter
. Hast du diesen dort gespeichert, gib unter
 und
und  ein. Wechsle wieder in das Y=-Menü und lass dir den zugehörigen Graph über DRAW anzeigen.
Wähle dann unter
ein. Wechsle wieder in das Y=-Menü und lass dir den zugehörigen Graph über DRAW anzeigen.
Wähle dann unter
_2015_a2_loesung_a3_casio.png) Also besitzt die Funktion
Also besitzt die Funktion  an der Stelle
an der Stelle  ein Minimum. Somit ist
ein Minimum. Somit ist  der Zeitpunkt im Intervall
der Zeitpunkt im Intervall ![\([0;12]\)](https://mathjax.schullv.de/5ba9b38204a320e9433651393178f89e741e0a72de8e09a0201574090d0733c6?color=5a5a5a) , an dem der Leistungsbedarf der Familie innerhalb dieses Kalenderjahres am stärksten abnimmt.
, an dem der Leistungsbedarf der Familie innerhalb dieses Kalenderjahres am stärksten abnimmt.
- Notwendige Bedingung:
- Hinreichende Bedingung:
SHIFT  F3 (V-Window)
F3 (V-Window)
die Intervallgrenzen
SHIFT  F5 (G-Solv)
F5 (G-Solv)  F2 (MAX)
F2 (MAX)
den Befehl zum Bestimmen des Maximums aus.
_2015_a2_loesung_a2_casio.png)
- Notwendige Bedingung:
- Hinreichende Bedingung:
SHIFT  F3 (V-Window)
F3 (V-Window)
die Intervallgrenzen
SHIFT  F5 (G-Solv)
F5 (G-Solv)  F3 (MIN)
F3 (MIN)
den Befehl zum Bestimmen des Minimums aus.
_2015_a2_loesung_a3_casio.png)
b)(1)
 Energiebedarf der Familie für das Kalenderjahr berechnen
Der Aufgabenstellung kannst du entnehmen, dass durch das Integral
Energiebedarf der Familie für das Kalenderjahr berechnen
Der Aufgabenstellung kannst du entnehmen, dass durch das Integral  der Energiebedarf der Familie im Zeitintervall
der Energiebedarf der Familie im Zeitintervall ![\([a;b]\)](https://mathjax.schullv.de/e84e12d6ffce2d83a82ceef8cfb5eb14688a4f4cce00a0d08d5357e2c6858142?color=5a5a5a) gegeben ist. Um den Energiebedarf für das Kalenderjahr zu berechnen, berechnest du das Integral mit den Grenzen
gegeben ist. Um den Energiebedarf für das Kalenderjahr zu berechnen, berechnest du das Integral mit den Grenzen  und
und  . Nutze dazu den Hauptsatz der Integralrechnung.
Setze die Grenzen in das Integral ein und berechne:
. Nutze dazu den Hauptsatz der Integralrechnung.
Setze die Grenzen in das Integral ein und berechne:
![\(\begin{array}[t]{rll}
\displaystyle\int_{0}^{12} g(t)\;\mathrm dt=&\displaystyle\int_{0}^{12} -t^4 + 26 \cdot t^3 -167,5 \cdot t^2 -12,5 \cdot t +2.053 \;\mathrm dt
\\[5pt]
=& \left[ - \dfrac{1}{5} \cdot t^5 + \dfrac{13}{2} \cdot t^4 -\dfrac{335}{6} \cdot t^3 -6,25 \cdot t^2 +2.053 \cdot t \right]_0^{12}
\\[5pt]
=&- \dfrac{1}{5} \cdot 12^5 + \dfrac{13}{2} \cdot 12^4 -\dfrac{335}{6} \cdot 12^3 -6,25 \cdot 12^2 +2.053 \cdot 12
\\[5pt]
=&-49.766,4 + 134.784 - 96.480 - 900 + 24.636
\\[5pt]
=& 12.273,6
\end{array}\)](https://mathjax.schullv.de/7c105122c81a23e288a2496d0b0590df4efda26434904bea11319f33aac75c00?color=5a5a5a) Also beträgt der Energiebedarf der Familie für das Kalenderjahr
Also beträgt der Energiebedarf der Familie für das Kalenderjahr  .
b)(2)
.
b)(2)
 Berechnen der Energie, die zum Heizen des Pools zur Verfügung steht
Der Pool wird mit der Energie geheizt, welche den Bedarf der Familie übersteigt. Diese Energie ist gerade die Differenz zwischen der von der Solaranlage erzeugten Energie und dem Energiebedarf der Familie. Zum Zeitpunkt
Berechnen der Energie, die zum Heizen des Pools zur Verfügung steht
Der Pool wird mit der Energie geheizt, welche den Bedarf der Familie übersteigt. Diese Energie ist gerade die Differenz zwischen der von der Solaranlage erzeugten Energie und dem Energiebedarf der Familie. Zum Zeitpunkt  ist diese Leistung somit durch
ist diese Leistung somit durch  gegeben. Für die überschüssige Energie im Intervall
gegeben. Für die überschüssige Energie im Intervall ![\(\left[3;9,5\right]\)](https://mathjax.schullv.de/a03ac5fe1f2ee83bfa4590b6a6c79fbf40a569515ebcc534bfeed1e72a1f310a?color=5a5a5a) berechne das Integral
berechne das Integral  . Berechne also zuerst
. Berechne also zuerst  . Danach kannst du per Hand oder mit deinem GTR weitermachen.
1. Schritt:
. Danach kannst du per Hand oder mit deinem GTR weitermachen.
1. Schritt:  berechnen
berechnen
![\(\begin{array}[t]{rll}
f(t)-g(t)&= \left(t^4-24 \cdot t^3 + 144 \cdot t^2 +400\right)-\left(-t^4 + 26 \cdot t^3 - 167,5 \cdot t^2 -12,5 \cdot t + 2.053\right) \\[5pt]
&=2\cdot t^4 - 50 \cdot t^3 + 311,5 \cdot t^2 +12,5 \cdot t -1.653
\end{array}\)](https://mathjax.schullv.de/f6eac637f555ff38ea83de9c273e93aba9395023388b03e70f09c825d19bf453?color=5a5a5a)
 Lösungsweg A: Per Hand
Bestimme nun eine Stammfunktion
Lösungsweg A: Per Hand
Bestimme nun eine Stammfunktion  und berechne damit das Integral
und berechne damit das Integral  .
2. Schritt: Stammfunktion
.
2. Schritt: Stammfunktion  bestimmen
bestimmen
![\(\begin{array}[t]{rll}
\displaystyle\int_{}^{} \left(f(t)-g(t)\right) \;\mathrm dt&=\displaystyle\int_{}^{}2\cdot t^4 - 50 \cdot t^3 + 311,5 \cdot t^2 +12,5 \cdot t -1.653 \;\mathrm dt\\[5pt]
&=\dfrac{1}{5}\cdot 2t^5-\dfrac{1}{4}\cdot 50t^4+ \dfrac{1}{3}\cdot 311,5t^3+\dfrac{1}{2}\cdot12,5t^2-1.653 t +c\\[5pt]
&=\dfrac{2}{5}t^5-\dfrac{25}{2}t^4+ \dfrac{623}{6}t^3 +\dfrac{25}{4}t^2-1.653 t +c
\end{array}\)](https://mathjax.schullv.de/254a2608a72d2a52686245f0652e715d8804574d5137d03f052bc76bb990cb20?color=5a5a5a) Wähle
Wähle  und damit ist
und damit ist  eine Stammfunktion von
eine Stammfunktion von  .
3. Schritt: Integral
.
3. Schritt: Integral  berechnen
berechnen
![\(\begin{array}[t]{rll}
\displaystyle\int_{3}^{9,5} \left(f(t)-g(t)\right) \;\mathrm dt&= (F-G)(9,5)-(F-G)(3)\\[5pt]
&=\left(\dfrac{2}{5}\cdot 9,5^5-\dfrac{25}{2}\cdot 9,5^4+ \dfrac{623}{6}\cdot 9,5^3+\dfrac{25}{4}\cdot 9,5^2-1.653 \cdot 9,5\right) \\[5pt]
&- \left(\dfrac{2}{5}\cdot 3^5-\dfrac{25}{2}\cdot 3^4+ \dfrac{623}{6}\cdot 3^3+\dfrac{25}{4}\cdot 3^2-1.653 \cdot 3\right)\\[5pt]
&= 3.022,62 - \left(-3014,55\right)\\[5pt]
&= 3.022,62 + 3014,55\\[5pt]
&= 6.037,173
\end{array}\)](https://mathjax.schullv.de/db79153c98144fa0d21114682e3004121eaf5e625746058eee33531f2ec70e75?color=5a5a5a) Der Familie stehen somit
Der Familie stehen somit  kWh Energie zum Heizen des Pools zur Verfügung.
kWh Energie zum Heizen des Pools zur Verfügung.
 Lösungsweg B: Lösen mit dem GTR
Wechsle mit deinem GTR in den Graph-Modus und speichere dort den Funktionsterm von
Lösungsweg B: Lösen mit dem GTR
Wechsle mit deinem GTR in den Graph-Modus und speichere dort den Funktionsterm von  . Hast du diesen dort gespeichert, gib unter
. Hast du diesen dort gespeichert, gib unter
 und
und  ein. Wechsle wieder in das Y=-Menü und lass dir den zugehörigen Graph über DRAW anzeigen.
Wähle dann unter
ein. Wechsle wieder in das Y=-Menü und lass dir den zugehörigen Graph über DRAW anzeigen.
Wähle dann unter
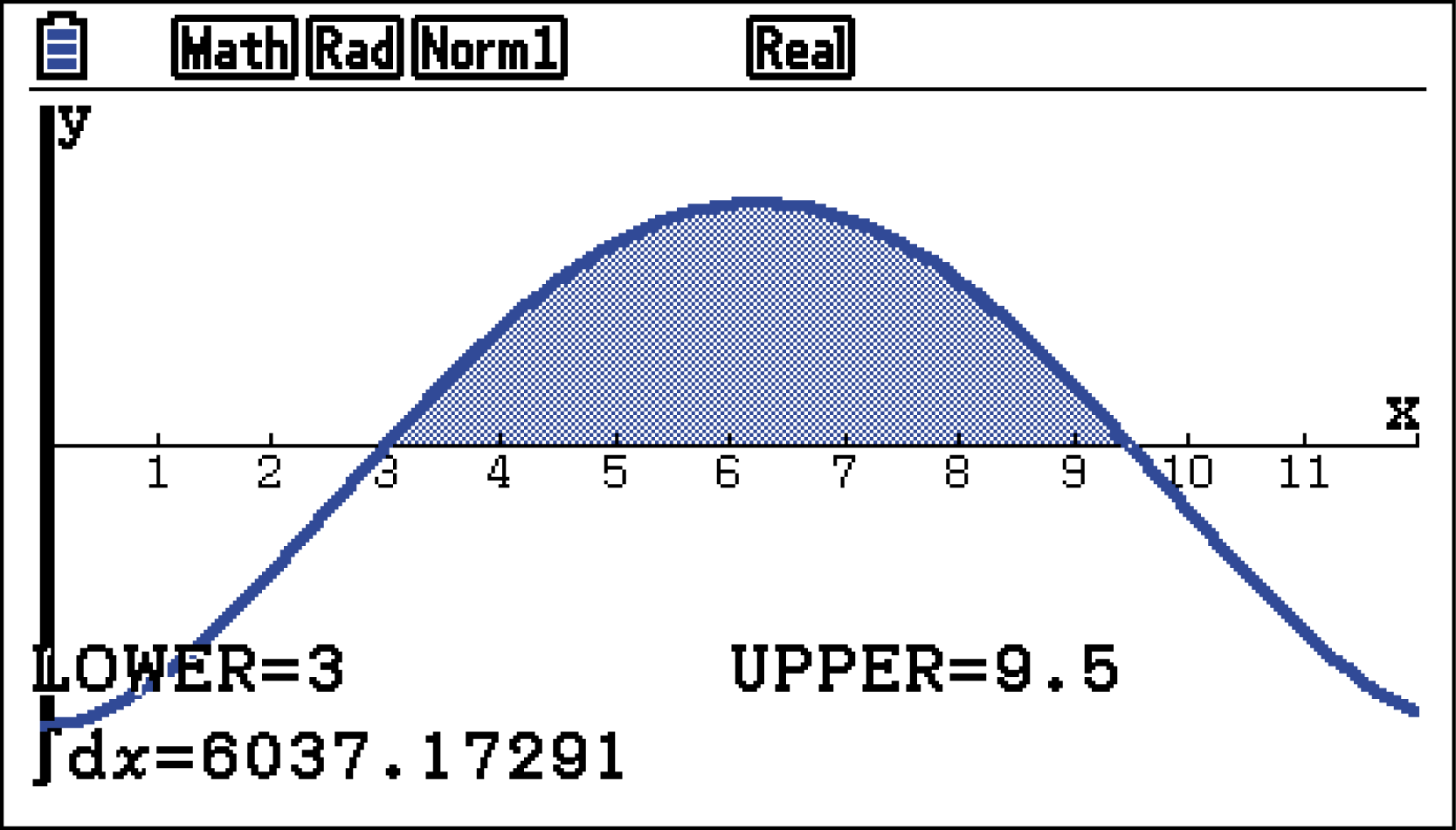 Der Familie stehen somit
Der Familie stehen somit  kWh Energie zum Heizen des Pools zur Verfügung.
kWh Energie zum Heizen des Pools zur Verfügung.
SHIFT  F3 (V-Window)
F3 (V-Window)
die Intervallgrenzen
SHIFT  F5 (G-Solv)
F5 (G-Solv)  F6
F6  F3 (
F3 ( dx)
dx)  F1 (
F1 ( dx)
dx)
den Befehl zum Berechnen des Integrals aus.

c)(1)
 Zeigen, dass
Zeigen, dass  eine der Funktionen
eine der Funktionen  ist und zugehöriges
ist und zugehöriges  berechnen
Hier musst du ein
berechnen
Hier musst du ein ![\(a \in [0,5 1,5]\)](https://mathjax.schullv.de/b56df50ba3a9c59c14365fa29be93a514101a315c7da4bf0b8981756721496c0?color=5a5a5a) finden, sodass
finden, sodass  gilt. Schaue dir dazu die beiden Funktionsgleichungen an und leite anhand des Koeffizienten des Terms mit der höchsten Ordnung ein
gilt. Schaue dir dazu die beiden Funktionsgleichungen an und leite anhand des Koeffizienten des Terms mit der höchsten Ordnung ein  her, für das du die Behauptung überprüfst und das zugehörige
her, für das du die Behauptung überprüfst und das zugehörige  berechnest.
Da
berechnest.
Da  der Term der höchsten Ordnung von
der Term der höchsten Ordnung von  und
und  ist, wähle
ist, wähle  so, dass diese dieselben Koeffizienten besitzen, also
so, dass diese dieselben Koeffizienten besitzen, also  . Damit gilt:
. Damit gilt:
 Somit hast du die Behauptung nachgewiesen. Berechne nun das zugehörige
Somit hast du die Behauptung nachgewiesen. Berechne nun das zugehörige  :
:
![\(\begin{array}[t]{rll}
w=& 116 - 66 \cdot a & \scriptsize \mid\; a=1 \text{ einsetzen}
\\[5pt]
=& 116 - 66
\\[5pt]
=& 50
\end{array}\)](https://mathjax.schullv.de/6da9b39b204a7256db09b3d6b4313d2de40dc16b3ea036bef46aa16452195380?color=5a5a5a) Also beträgt der zugehörige Neigungswinkel
Also beträgt der zugehörige Neigungswinkel  .
c)(2)
.
c)(2)
 Maximale in einem Jahr aus der Solaranlage abrufbare Energie für
Maximale in einem Jahr aus der Solaranlage abrufbare Energie für  nachweisen
Berechne zunächst die für ein beliebiges
nachweisen
Berechne zunächst die für ein beliebiges  innerhalb eines Jahres abrufbare Energie durch das Integral
innerhalb eines Jahres abrufbare Energie durch das Integral  . Ermittle für die erhaltene, von
. Ermittle für die erhaltene, von  abhängige Funktion das Maximum über
abhängige Funktion das Maximum über  . Erhältst du daraus
. Erhältst du daraus  , hast du die Behauptung nachgewiesen.
1. Schritt: Integral
, hast du die Behauptung nachgewiesen.
1. Schritt: Integral  berechnen
Mit dem Hauptsatz der Integralrechnung ergibt sich:
berechnen
Mit dem Hauptsatz der Integralrechnung ergibt sich:
![\(\begin{array}[t]{rll}
\displaystyle\int_0^{12} f_a(t) \;\mathrm dt=& \displaystyle\int_0^{12} a \cdot \left(t^4-24 \cdot t^3 + 144 \cdot t^2 +400\right) - 400 \cdot \left(a^2 -1 \right) \;\mathrm dt
\\[5pt]
=&\left[a \cdot \left(\dfrac{1}{5} \cdot t^5 - 6 \cdot t^4 + 48 \cdot t^3 +400 \cdot t \right) - 400 \cdot \left(a^2 -1 \right) \cdot t \right]_0^{12}
\\[5pt]
=&a \cdot \left(\dfrac{1}{5} \cdot 12^5 - 6 \cdot 12^4 + 48 \cdot 12^3 +400 \cdot 12 \right) - 400 \cdot \left(a^2 -1 \right) \cdot 12
\\[5pt]
=& a \cdot \left( \dfrac{65.472}{5}\right) - 4.800 \cdot \left(a^2 -1 \right)
\\[5pt]
=&:E(a)
\end{array}\)](https://mathjax.schullv.de/df431607d71ee5e24e56ea62163aeeb7c54713e0b77980cc3ace6fecd39b19f9?color=5a5a5a) Die Funktion
Die Funktion  gibt dir nun die in einem Jahr aus der Solaranlage abrufbare Energie in Abhängigkeit von
gibt dir nun die in einem Jahr aus der Solaranlage abrufbare Energie in Abhängigkeit von  an. Ermittle also das Maximum von
an. Ermittle also das Maximum von  . Dies kannst du per Hand oder mit deinem GTR erledigen.
2. Schritt: Maximum von
. Dies kannst du per Hand oder mit deinem GTR erledigen.
2. Schritt: Maximum von  bestimmen
bestimmen
 Lösungsweg A: Per Hand
Bestimme das Maximum von
Lösungsweg A: Per Hand
Bestimme das Maximum von  , indem du zunächst die notwendige Bedingung anwendest. Bei der Funktion
, indem du zunächst die notwendige Bedingung anwendest. Bei der Funktion  handelt es sich um eine nach unten geöffnete Parabel. Somit fällt die Überprüfung der hinreichenden Bedingung weg und auch die Überprüfung der Randwerte ist hinfällig.
handelt es sich um eine nach unten geöffnete Parabel. Somit fällt die Überprüfung der hinreichenden Bedingung weg und auch die Überprüfung der Randwerte ist hinfällig.

 Ableitung von
Ableitung von  ermitteln
Leite
ermitteln
Leite  nach
nach  ab:
ab:

 Notwendige Bedingung anwenden
Setze den Funktionsterm der
Notwendige Bedingung anwenden
Setze den Funktionsterm der  Ableitung
Ableitung  gleich Null, um mögliche Nullstellen zu bestimmen:
gleich Null, um mögliche Nullstellen zu bestimmen:
![\(\begin{array}[t]{rll}
E‘(a)\stackrel{!}=&0&\scriptsize \mid\; E‘(a) \text{ einsetzen}
\\[5pt]
\dfrac{65.472}{5} - 9.600 \cdot a =&0&\scriptsize \mid\; +9.600 \cdot a
\\[5pt]
\dfrac{65.472}{5}=&9.600 \cdot a &\scriptsize \mid\; :9.600
\\[5pt]
\dfrac{341}{250}=&a
\\[5pt]
1,364=&a
\end{array}\)](https://mathjax.schullv.de/a3e46c7e5db14a8029404d4b26bb9bbc5acf5c667c206560e77ce23a671c9cde?color=5a5a5a) Damit kommt nur
Damit kommt nur  als Maximum in Frage. Aufgrund der Parabelform von
als Maximum in Frage. Aufgrund der Parabelform von  besitzt die Funktion an der Stelle
besitzt die Funktion an der Stelle  eine Maximalstelle.
Damit hast du nachgewiesen, dass die in einem Jahr aus der Solaranlage abrufbare Energie für
eine Maximalstelle.
Damit hast du nachgewiesen, dass die in einem Jahr aus der Solaranlage abrufbare Energie für 
 am größten ist.
am größten ist.
 Lösungsweg B: Lösen mit dem GTR
Wechsle mit deinem GTR in das Y=-Menü und speichere dort den Funktionsterm von
Lösungsweg B: Lösen mit dem GTR
Wechsle mit deinem GTR in das Y=-Menü und speichere dort den Funktionsterm von  . Hast du diesen dort gespeichert, gib unter
. Hast du diesen dort gespeichert, gib unter
 und
und  ein. Wechsle wieder in das Y=-Menü und lass dir den zugehörigen Graph über DRAW anzeigen.
Wähle dann unter
ein. Wechsle wieder in das Y=-Menü und lass dir den zugehörigen Graph über DRAW anzeigen.
Wähle dann unter
_2015_a2_loesung_c2_casio.png) Damit hast du nachgewiesen, dass die in einem Jahr aus der Solaranlage abrufbare Energie für
Damit hast du nachgewiesen, dass die in einem Jahr aus der Solaranlage abrufbare Energie für 
 am größten ist.
c)(3)
am größten ist.
c)(3)
 Behauptung des Solaranlagenherstellers begründen
Abbildung 2 liefert dir den Graphen
Behauptung des Solaranlagenherstellers begründen
Abbildung 2 liefert dir den Graphen  für den Neigungswinkel
für den Neigungswinkel  und den Graphen
und den Graphen  für
für  . Die von der Solaranlage mit dem entsprechenden Neigungswinkel bereitgestellte Energie wird durch die Flächen unterhalb der entsprechenden Graphen dargestellt. Zudem ist der Energiebedarf der Familie durch die Fläche unterhalb des Graphen der Funktion
. Die von der Solaranlage mit dem entsprechenden Neigungswinkel bereitgestellte Energie wird durch die Flächen unterhalb der entsprechenden Graphen dargestellt. Zudem ist der Energiebedarf der Familie durch die Fläche unterhalb des Graphen der Funktion  dargestellt.
Nun erkennst du anhand der Abbildung 2, dass die Fläche unterhalb des Graphen von
dargestellt.
Nun erkennst du anhand der Abbildung 2, dass die Fläche unterhalb des Graphen von  einen größeren Anteil an der Fläche unterhalb von
einen größeren Anteil an der Fläche unterhalb von  überdeckt als die Fläche unterhalb von
überdeckt als die Fläche unterhalb von  .
Damit deckt über das ganze Kalenderjahr die Solaranlage mit Neigungswinkel
.
Damit deckt über das ganze Kalenderjahr die Solaranlage mit Neigungswinkel  einen höheren Anteil am Leistungsbedarf der Familie als die Solaranlage mit Neigungswinkel
einen höheren Anteil am Leistungsbedarf der Familie als die Solaranlage mit Neigungswinkel  .
.
SHIFT  F3 (V-Window)
F3 (V-Window)
die Intervallgrenzen
SHIFT  F5 (G-Solv)
F5 (G-Solv)  F2 (MAX)
F2 (MAX)
den Befehl zum Bestimmen des Maximums aus.
_2015_a2_loesung_c2_casio.png)