Aufgabe 3
Aufgabenstellung
Für jede von Null verschiedene reelle Zahl  ist
ist  die Funktion mit der Gleichung
die Funktion mit der Gleichung  ,
,  .
.
Für erhält man die Funktion
erhält man die Funktion  mit der Gleichung
mit der Gleichung  ,
,  und für
und für  die Funktion
die Funktion  mit der Gleichung
mit der Gleichung  ,
,  .
.
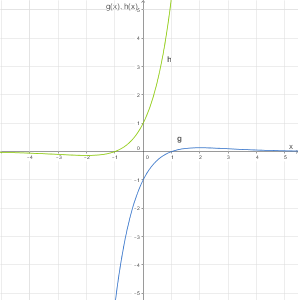
Die Graphen von und
und  sind in der Abbildung dargestellt.
sind in der Abbildung dargestellt.
Für
Die Graphen von
a)
(1)
Zeige, dass  die einzige Nullstelle von
die einzige Nullstelle von  ist.
ist.
(2P)
(2)
Bestimme in Abhängigkeit von  die Koordination der lokalen Extrem- und Wendepunkte des Graphen der Funktion
die Koordination der lokalen Extrem- und Wendepunkte des Graphen der Funktion  .
.
Gib die Art der Extrempunkte an.
[Zur Kontrolle: .]
.]
Gib die Art der Extrempunkte an.
[Zur Kontrolle:
(15P)
b)
(1)
Der Graph der Funktion  schneidet die
schneidet die  -Achse im Punkt
-Achse im Punkt  .
.
Gib die Koordinaten von an.
an.
Gib die Koordinaten von
(2P)
(2)
Bestimme eine Gleichung der Tangente  an den Graphen der Funktion
an den Graphen der Funktion  im Punkt
im Punkt  .
.
[Zur Kontrolle: ,
,  .]
.]
[Zur Kontrolle:
(2P)
(3)
Die Tangente  und die Koordinatenachsen bilden ein Dreieck.
und die Koordinatenachsen bilden ein Dreieck.
Berechne die Dreiecksfläche in Abhängigkeit von
in Abhängigkeit von  .
.
Berechne die Dreiecksfläche
(4P)
c)
(1)
Ermittle mit Hilfe von Integrationsverfahren eine Stammfunktion der Funktion  .
.
[Zur Kontrolle: Zum Beispiel ist die Funktion mit der Gleichung
mit der Gleichung  ,
,  , eine Stammfunktion von
, eine Stammfunktion von  .]
.]
[Zur Kontrolle: Zum Beispiel ist die Funktion
(4P)
(2)
Bestimme in Abhängigkeit von  den Inhalt
den Inhalt  der Fläche, die von dem Graphen der Funktion
der Fläche, die von dem Graphen der Funktion  und den beiden Koordinatenachsen eingeschlossen wird.
und den beiden Koordinatenachsen eingeschlossen wird.
Berechne alle , für die
, für die  gilt.
gilt.
 Zur Kontrolle:
Zur Kontrolle:  .
.![\(\big]\)](https://mathjax.schullv.de/0c6dff9ed6a80b0cc013679b53aff551dd11abb4691ba32076d10b15d6195a5d?color=5a5a5a)
Berechne alle
(5P)
d)
Betrachte nun die Funktionen  und
und  .
.
Bildnachweise [nach oben]
(1)
Weise nach, dass  für alle
für alle  gilt.
gilt.
Interpretiere diese Aussage geometrisch.
Interpretiere diese Aussage geometrisch.
(4P)
(2)
Beweise: Es gilt  für alle
für alle  .
.
(4P)
(3)
Für alle  sei
sei  die Parallele zur
die Parallele zur  -Achse durch den Punkt
-Achse durch den Punkt  .
.
Es sei der Inhalt der Fläche, die von den Graphen der Funktionen
der Inhalt der Fläche, die von den Graphen der Funktionen  und
und  , der
, der  -Achse und
-Achse und  eingeschlossen wird.
eingeschlossen wird.
Zeige: Es gilt ) für alle
) für alle  .
.
Begründe, dass die Funktion mit der Gleichung
mit der Gleichung  ),
),  streng monoton steigend ist.
streng monoton steigend ist.
Es sei
Zeige: Es gilt
Begründe, dass die Funktion
(8P)
© 2016 - SchulLV.
a)
(1)
(2)
- Notwendiges Kriterium:
- Hinreichendes Kriterium:
: Bei
liegt ein Hochpunkt.
: Bei
liegt ein Tiefpunkt.
- Bilde die ersten beiden Ableitungsfunktionen von
.
- Wende das notwendige Kriterium an, um mögliche Extremstellen zu bestimmen.
- Überprüfe das hinreichende Kriterium und bestimme so die Art der Extrempunkte.
- Berechne die vollständigen Koordinaten durch Einsetzen der Extremstellen in
.
- Notwendiges Kriterium:
- Hinreichendes Kriterium:
- Bilde die dritte Ableitung
.
- Bestimme mit dem notwendigen Kriterium mögliche Wendestellen von
.
- Überprüfe das hinreichende Kriterium.
- Berechne die zugehörigen
-Koordinaten.
b)
(1)
(2)
- Der Punkt
liegt auf
.
besitzt die gleiche Steigung wie der Graph von
im Punkt
.
(3)
Für die Berechnung des Flächeninhalts ist es hilfreich, das Dreieck in dem Schaubild zu skizzieren.
Das Dreieck wird vom Ursprung  und den Schnittpunkten der Tangente mit den Koordinatenachsen begrenzt. Da die Koordinatenachsen rechtwinklig zueinander stehen, kannst du den Flächeninhalt wie folgt berechnen:
und den Schnittpunkten der Tangente mit den Koordinatenachsen begrenzt. Da die Koordinatenachsen rechtwinklig zueinander stehen, kannst du den Flächeninhalt wie folgt berechnen:
 Die Längen der Strecken
Die Längen der Strecken  und
und  ergeben sich über den Betrag der
ergeben sich über den Betrag der  -Koordinate von
-Koordinate von  bzw. der
bzw. der  -Koordinate von
-Koordinate von  . Die Koordinaten von
. Die Koordinaten von  kennst du bereits, also ist
kennst du bereits, also ist  .
.
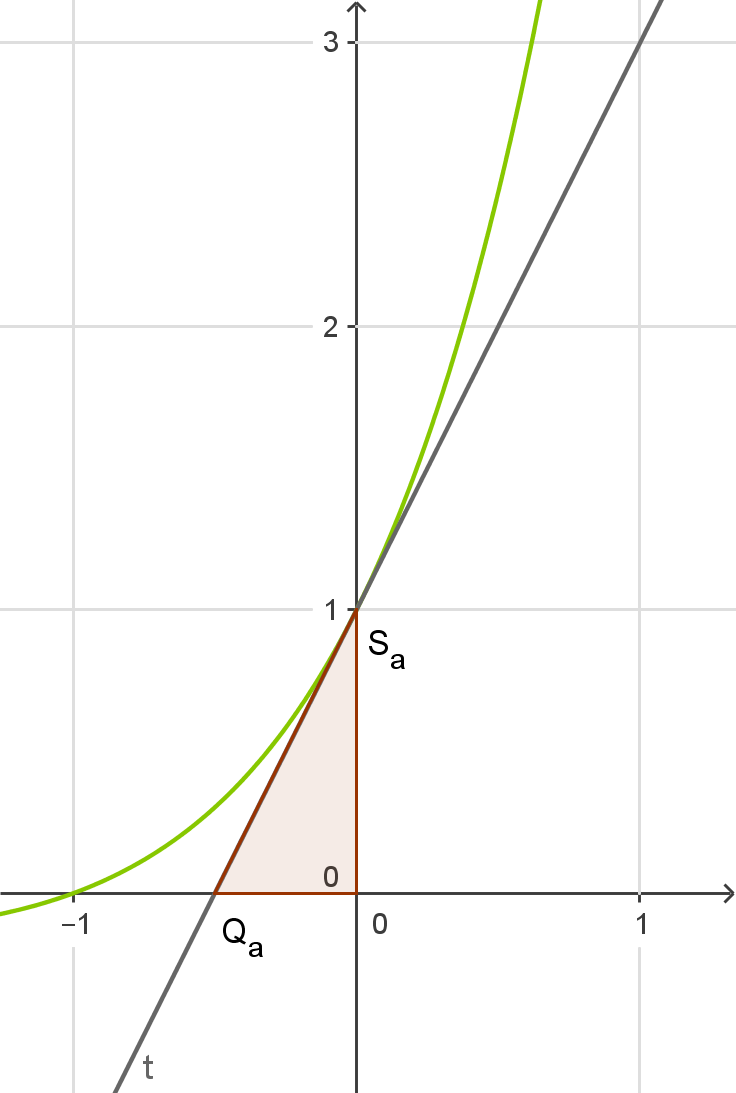 Abb. 1: Dreieck
Abb. 1: Dreieck
c)
(1)
(2)
Gesucht ist hier der Flächeninhalt zwischen dem Graphen von  und der
und der  -Achse. Nach links ist diese Fläche durch die Nullstelle
-Achse. Nach links ist diese Fläche durch die Nullstelle  von
von  begrenzt, nach rechts durch die
begrenzt, nach rechts durch die  -Achse. Du kannst den gesuchten Flächeninhalt daher über folgendes Integral berechnen:
-Achse. Du kannst den gesuchten Flächeninhalt daher über folgendes Integral berechnen:
 Zur Berechnung des Integrals kannst du die oben bestimmte Stammfunktion verwenden.
Zur Berechnung des Integrals kannst du die oben bestimmte Stammfunktion verwenden.
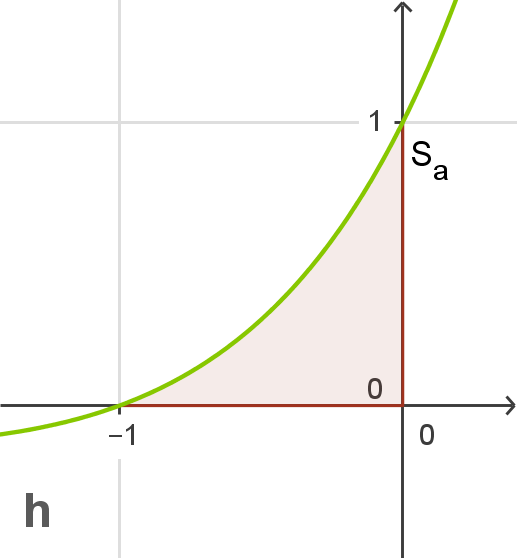 Abb. 2: Fläche unter dem Graphen
Abb. 2: Fläche unter dem Graphen
d)
(1)
(2)
(3)
Gesucht ist der Inhalt der Fläche zwischen den beiden Graphen von  und
und  , die nach links von der
, die nach links von der  -Achse und nach rechts durch die Parallele zur
-Achse und nach rechts durch die Parallele zur  -Achse durch den Punkt
-Achse durch den Punkt  begrenzt wird.
Den Inhalt einer Fläche zwischen zwei Graphen kannst du mit Hilfe eines Integrals über die Differenz dieser beiden Funktionen berechnen. Mit den Grenzen
begrenzt wird.
Den Inhalt einer Fläche zwischen zwei Graphen kannst du mit Hilfe eines Integrals über die Differenz dieser beiden Funktionen berechnen. Mit den Grenzen  und
und  ergibt sich daher folgendes Integral:
ergibt sich daher folgendes Integral:
 Da du oben gezeigt hast, dass
Da du oben gezeigt hast, dass  für alle
für alle  ist, weißt du, dass der Graph von
ist, weißt du, dass der Graph von  im betrachteten Intervall (
im betrachteten Intervall ( ) über dem von
) über dem von  liegt. Daher kannst du dieses Integral in zwei Integrale aufteilen.
liegt. Daher kannst du dieses Integral in zwei Integrale aufteilen.
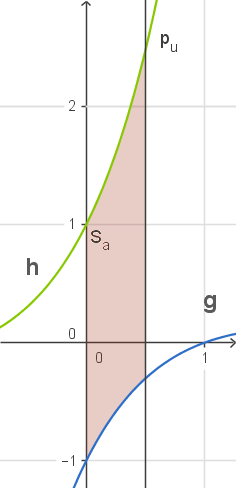 Abb. 3: Fläche zwischen den Graphen
Abb. 3: Fläche zwischen den Graphen
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
a)
(1)
(2)
- Notwendiges Kriterium:
- Hinreichendes Kriterium:
: Bei
liegt ein Hochpunkt.
: Bei
liegt ein Tiefpunkt.
- Bilde die ersten beiden Ableitungsfunktionen von
.
- Wende das notwendige Kriterium an, um mögliche Extremstellen zu bestimmen.
- Überprüfe das hinreichende Kriterium und bestimme so die Art der Extrempunkte.
- Berechne die vollständigen Koordinaten durch Einsetzen der Extremstellen in
.
- Notwendiges Kriterium:
- Hinreichendes Kriterium:
- Bilde die dritte Ableitung
.
- Bestimme mit dem notwendigen Kriterium mögliche Wendestellen von
.
- Überprüfe das hinreichende Kriterium.
- Berechne die zugehörigen
-Koordinaten.
b)
(1)
(2)
- Der Punkt
liegt auf
.
besitzt die gleiche Steigung wie der Graph von
im Punkt
.
(3)
Für die Berechnung des Flächeninhalts ist es hilfreich, das Dreieck in dem Schaubild zu skizzieren.
Das Dreieck wird vom Ursprung  und den Schnittpunkten der Tangente mit den Koordinatenachsen begrenzt. Da die Koordinatenachsen rechtwinklig zueinander stehen, kannst du den Flächeninhalt wie folgt berechnen:
und den Schnittpunkten der Tangente mit den Koordinatenachsen begrenzt. Da die Koordinatenachsen rechtwinklig zueinander stehen, kannst du den Flächeninhalt wie folgt berechnen:
 Die Längen der Strecken
Die Längen der Strecken  und
und  ergeben sich über den Betrag der
ergeben sich über den Betrag der  -Koordinate von
-Koordinate von  bzw. der
bzw. der  -Koordinate von
-Koordinate von  . Die Koordinaten von
. Die Koordinaten von  kennst du bereits, also ist
kennst du bereits, also ist  .
.
 Abb. 1: Dreieck
Abb. 1: Dreieck
c)
(1)
(2)
Gesucht ist hier der Flächeninhalt zwischen dem Graphen von  und der
und der  -Achse. Nach links ist diese Fläche durch die Nullstelle
-Achse. Nach links ist diese Fläche durch die Nullstelle  von
von  begrenzt, nach rechts durch die
begrenzt, nach rechts durch die  -Achse. Du kannst den gesuchten Flächeninhalt daher über folgendes Integral berechnen:
-Achse. Du kannst den gesuchten Flächeninhalt daher über folgendes Integral berechnen:
 Zur Berechnung des Integrals kannst du die oben bestimmte Stammfunktion verwenden.
Zur Berechnung des Integrals kannst du die oben bestimmte Stammfunktion verwenden.
 Abb. 2: Fläche unter dem Graphen
Abb. 2: Fläche unter dem Graphen
d)
(1)
(2)
(3)
Gesucht ist der Inhalt der Fläche zwischen den beiden Graphen von  und
und  , die nach links von der
, die nach links von der  -Achse und nach rechts durch die Parallele zur
-Achse und nach rechts durch die Parallele zur  -Achse durch den Punkt
-Achse durch den Punkt  begrenzt wird.
Den Inhalt einer Fläche zwischen zwei Graphen kannst du mit Hilfe eines Integrals über die Differenz dieser beiden Funktionen berechnen. Mit den Grenzen
begrenzt wird.
Den Inhalt einer Fläche zwischen zwei Graphen kannst du mit Hilfe eines Integrals über die Differenz dieser beiden Funktionen berechnen. Mit den Grenzen  und
und  ergibt sich daher folgendes Integral:
ergibt sich daher folgendes Integral:
 Da du oben gezeigt hast, dass
Da du oben gezeigt hast, dass  für alle
für alle  ist, weißt du, dass der Graph von
ist, weißt du, dass der Graph von  im betrachteten Intervall (
im betrachteten Intervall ( ) über dem von
) über dem von  liegt. Daher kannst du dieses Integral in zwei Integrale aufteilen.
liegt. Daher kannst du dieses Integral in zwei Integrale aufteilen.
 Abb. 3: Fläche zwischen den Graphen
Abb. 3: Fläche zwischen den Graphen
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.