Aufgabe 1
In einem Entwicklungslabor wird der Ladevorgang bei Akkus an verschiedenen Ladegeräten getestet. Der zeitliche Verlauf des Ladezustands für verschiedene Ladegeräte wird durch Funktionen  mit
mit 

 modelliert und ist für
modelliert und ist für 

 und
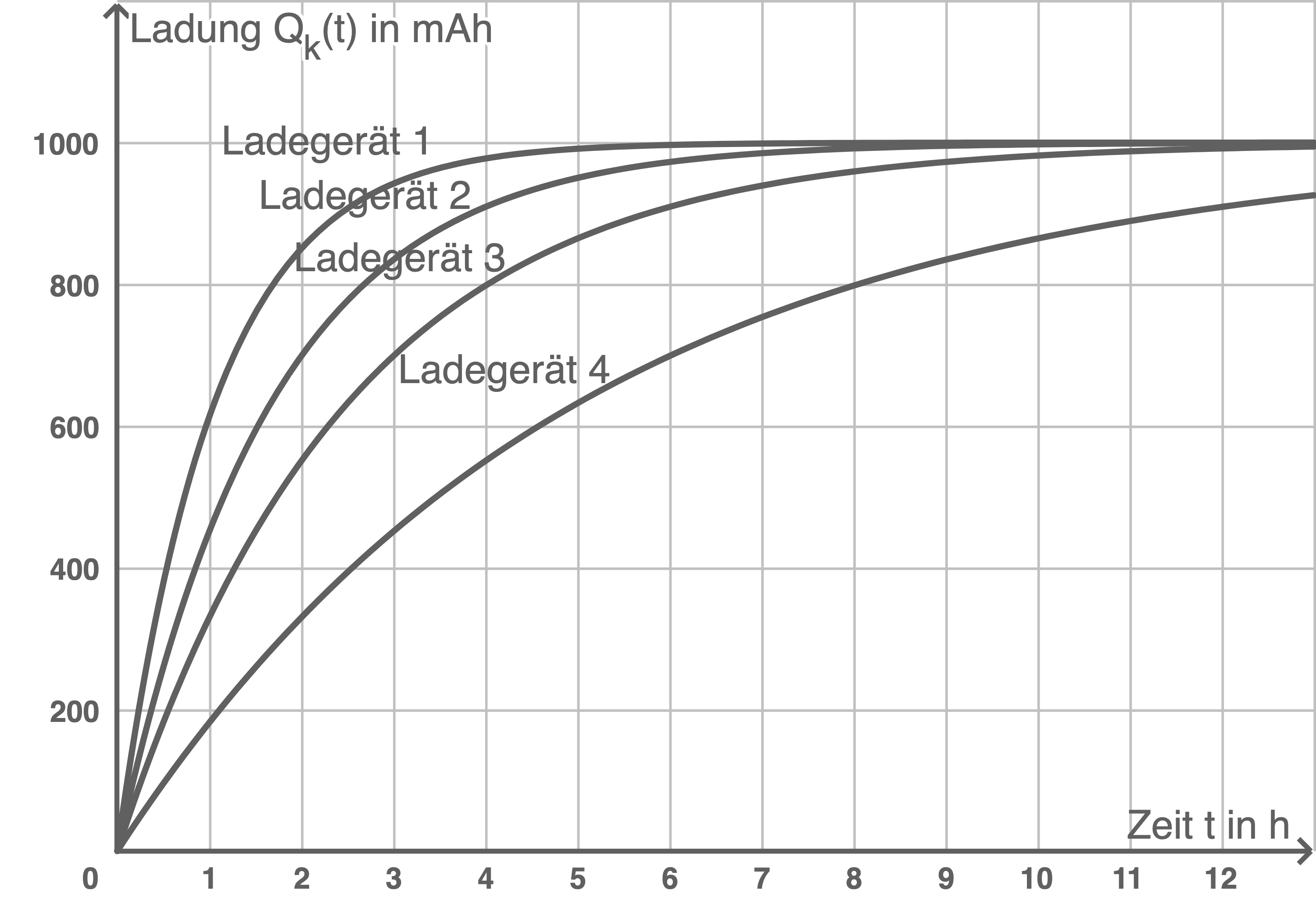
und  in Abbildung 1 dargestellt.
in Abbildung 1 dargestellt.
 Dabei gibt
Dabei gibt  die seit Beginn des Ladevorgangs vergangene Zeit in Stunden und
die seit Beginn des Ladevorgangs vergangene Zeit in Stunden und  die Ladung des Akkus zum Zeitpunkt
die Ladung des Akkus zum Zeitpunkt  (Einheit:
(Einheit:  ) an.
) an.
Der Ladevorgang beginnt im Folgenden stets zum Zeitpunkt und es gilt
und es gilt  d. h., in der Modellierung wird vereinfachend davon ausgegangen, dass die Ladung des Akkus zu Beginn immer den Wert
d. h., in der Modellierung wird vereinfachend davon ausgegangen, dass die Ladung des Akkus zu Beginn immer den Wert  hat.
hat.
 Eine Balkenanzeige am Ladegerät signalisiert während des Ladevorgangs den momentanen Ladezustand des Akkus mit folgenden Symbolen:
Die momentane Änderungsrate der Ladung
Eine Balkenanzeige am Ladegerät signalisiert während des Ladevorgangs den momentanen Ladezustand des Akkus mit folgenden Symbolen:
Die momentane Änderungsrate der Ladung  wird Ladestrom
wird Ladestrom  genannt (Einheit:
genannt (Einheit:  ).
).
Der Ladestrom wird zur Kontrolle des Ladungsvorgangs benutzt. In diesem Falle lautet also die Funktionsgleichung für den Ladestrom:

Abbildung 1
Der Ladevorgang beginnt im Folgenden stets zum Zeitpunkt
a)
(1)
Der Verlauf des Graphen legt die Vermutung nahe, dass sich die Funktionen  für große Werte von
für große Werte von  unabhängig von
unabhängig von  dem Wert
dem Wert  annähern und ihn nicht überschreiten. Entscheide begründet, ob diese Vermutung wahr ist.
annähern und ihn nicht überschreiten. Entscheide begründet, ob diese Vermutung wahr ist.
Die maximale Ladung, die ein Akku unter idealen Bedingungen aufnehmen kann, wird Kapazität genannt. Im Folgenden haben die betrachteten Akkus jeweils eine Kapazität von
kein Balken:
Die Ladung beträgt weniger als  der Kapazität.
der Kapazität.
ein Balken:
Die Ladung beträgt mindestens  und weniger als
und weniger als  der Kapazität.
der Kapazität.
zwei Balken:
Die Ladung beträgt mindestens  und weniger als
und weniger als  der Kapazität.
der Kapazität.
drei Balken:
Die Ladung beträgt mindestens  der Kapazität.
der Kapazität.
(2)
Bestimme in Abhängigkeit von  wie lange es ab dem Start des Ladevorgangs dauert, bis die Balkenanzeige den ersten Balken anzeigt. Begründe anschaulich, ggf. mit Abbildung 1, dass die Zeitdauer bis zum Erscheinen eines weiteren Balkens von Balken zu Balken immer größer wird.
wie lange es ab dem Start des Ladevorgangs dauert, bis die Balkenanzeige den ersten Balken anzeigt. Begründe anschaulich, ggf. mit Abbildung 1, dass die Zeitdauer bis zum Erscheinen eines weiteren Balkens von Balken zu Balken immer größer wird.
(3)
Beschreibe die Bedeutung größer werdender Werte für den Parameter  im Sachzusammenhang und gib begründet an, welcher Graph in Abbildung 1 zum Parameter
im Sachzusammenhang und gib begründet an, welcher Graph in Abbildung 1 zum Parameter  gehört.
gehört.
(3 + 5 + 3 Punkte)
Der Ladestrom wird zur Kontrolle des Ladungsvorgangs benutzt. In diesem Falle lautet also die Funktionsgleichung für den Ladestrom:
b)
(1)
Um den Akku zu schonen, soll der Ladestrom während des Ladevorgangs nicht zu groß werden.
Begründe, dass der Ladestrom in einem beliebigen Zeitintervall jeweils am Intervallrand maximal ist, und gib begründet an, an welchem der beiden Intervallränder das Maximum liegt.
Begründe, dass der Ladestrom in einem beliebigen Zeitintervall jeweils am Intervallrand maximal ist, und gib begründet an, an welchem der beiden Intervallränder das Maximum liegt.
(2)
Für den vorliegenden Akku soll der Ladestrom während des Ladevorgangs den Wert  zu keinem Zeitpunkt überschreiten.
zu keinem Zeitpunkt überschreiten.
Bestimme, für welche Werte von die Vorgabe eingehalten wird. Gib an, welche der Ladegeräte aus a) die Vorgabe nicht erfüllen.
die Vorgabe eingehalten wird. Gib an, welche der Ladegeräte aus a) die Vorgabe nicht erfüllen.
Bestimme, für welche Werte von
(3)
Der Ladevorgang wird abgeschaltet, wenn der Ladestrom  den Wert
den Wert  unterschreitet.
unterschreitet.
Bestimme die von abhängige Dauer eines solches Ladevorgangs. Zeige, dass die Abschaltbedingung bewirkt, dass der Ladevorgang unabhängig von
abhängige Dauer eines solches Ladevorgangs. Zeige, dass die Abschaltbedingung bewirkt, dass der Ladevorgang unabhängig von  immer in dem Moment abgeschaltet wird, wenn die Anzeige zum letzten Balken wechselt.
immer in dem Moment abgeschaltet wird, wenn die Anzeige zum letzten Balken wechselt.
Bestimme die von
(3+ 3+ 5 Punkte)
c)
Ein defektes Ladegerät steuert den Ladestrom fälschlicherweise nach der Funktionsvorschrift 
Nach Stunden wird der Ladevorgang an diesem Ladegerät abgebrochen.
Stunden wird der Ladevorgang an diesem Ladegerät abgebrochen.
Nach
(1)
Zeige rechnerisch, dass die Funktion  genau ein lokales Maximum besitzt.
genau ein lokales Maximum besitzt.
(2)
Begründe, dass der Ladestrom  während des Ladevorgangs den Wert
während des Ladevorgangs den Wert  nie überschreitet.
nie überschreitet.
(7 + 2 Punkte)
d)
Ein Powerladegerät soll den Akku schnell aufladen. Dazu wird der Akku zunächst mit einem konstanten Ladestrom von  geladen, bis der Akku eine Ladung von
geladen, bis der Akku eine Ladung von  erreicht hat. Ab diesem Zeitpunkt
erreicht hat. Ab diesem Zeitpunkt  wird der Ladestrom gemäß der Funktion
wird der Ladestrom gemäß der Funktion  mit
mit  verringert bis zum Zeitpunkt
verringert bis zum Zeitpunkt  wenn der Wert
wenn der Wert  erreicht wird und der Ladevorgang abgeschaltet wird. Ein solcher Ladevorgang ist in Abbildung 2 dargestellt.
erreicht wird und der Ladevorgang abgeschaltet wird. Ein solcher Ladevorgang ist in Abbildung 2 dargestellt.
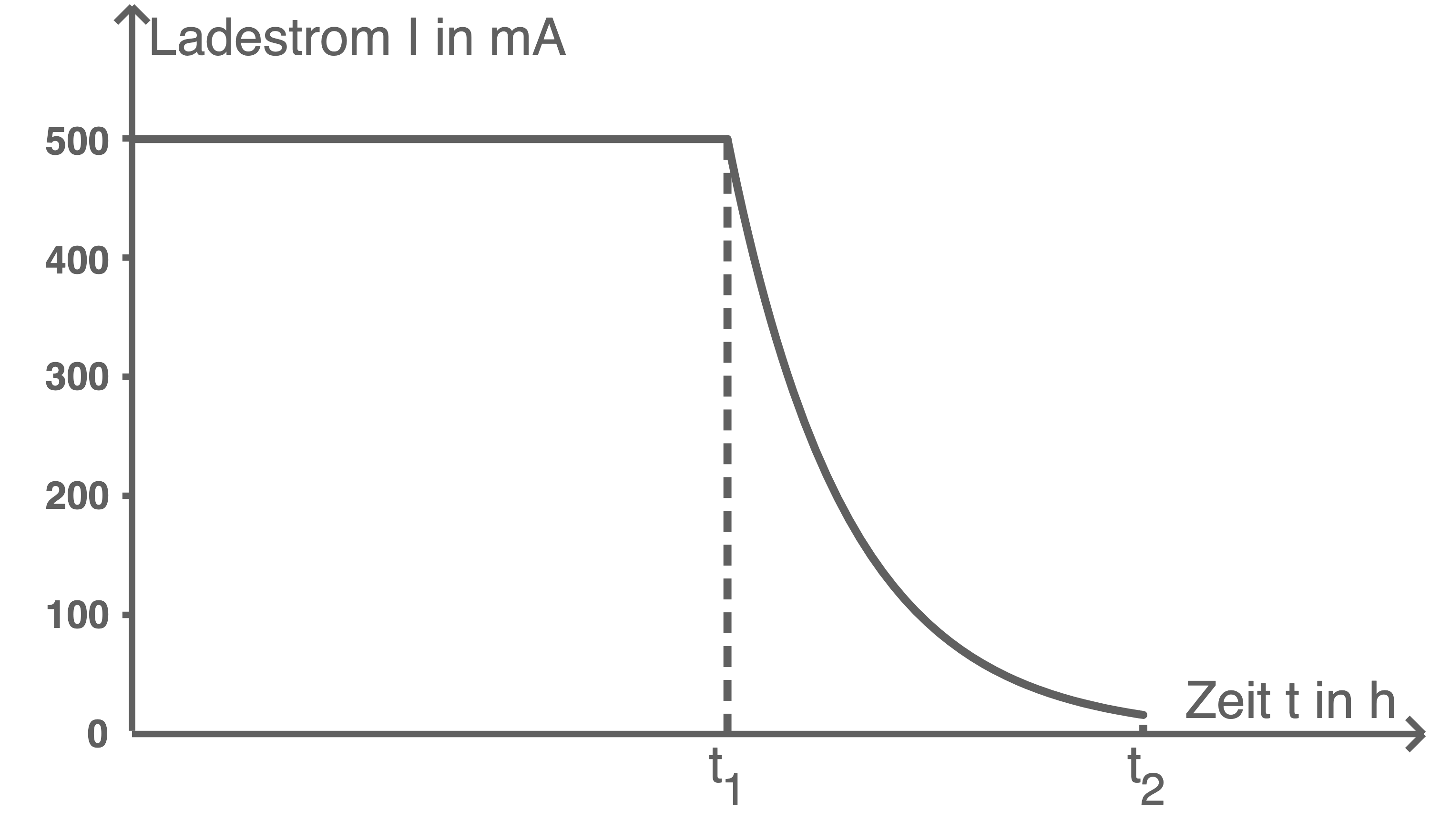

Abbildung 2
(1)
Bestimme die Dauer des gesamten Ladevorgangs.
 Zur Kontrolle: ca.
Zur Kontrolle: ca.  [Stunden]
[Stunden] ![\(\big]\)](https://mathjax.schullv.de/0c6dff9ed6a80b0cc013679b53aff551dd11abb4691ba32076d10b15d6195a5d?color=5a5a5a)
(2)
Bestimme die Gesamtladung  des Akkus am Ende des Ladevorgangs.
des Akkus am Ende des Ladevorgangs.
(4 + 5 Punkte)
a)
(1)
Es gilt:  Da
Da  folgt
folgt  Daraus folgt
Daraus folgt  woraus sich ergibt, dass
woraus sich ergibt, dass  Die Werte der Funktionen
Die Werte der Funktionen  überschreiten somit nie den Wert
überschreiten somit nie den Wert 
Die Vermutung ist also wahr.
Die Vermutung ist also wahr.
(2)
Der erste Balken erscheint, wenn mindestens  des Akkus geladen sind, wenn also die Ladung
des Akkus geladen sind, wenn also die Ladung  beträgt.
beträgt.
![\(\begin{array}[t]{rll}
Q_k(t) &=& 330 \\[5pt]
1000\cdot(1-\mathrm e^{-k\cdot t}) &=& 330 &\quad \scriptsize \mid\;:1.000 \\[5pt]
1-\mathrm e^{-k\cdot t}&=& 0,33 &\quad \scriptsize \mid\;-1 \\[5pt]
-\mathrm e^{-k\cdot t}&=& -0,67 &\quad \scriptsize \mid\; \cdot (-1)\\[5pt]
\mathrm e^{-k\cdot t}&=& 0,67 &\quad \scriptsize \mid\;\ln \\[5pt]
-k\cdot t&=& \ln (0,67)&\quad \scriptsize \mid\;:(-k) \\[5pt]
t&=& -\frac{\ln (0,67)}{k}
\end{array}\)](https://mathjax.schullv.de/a460a3a30f800488246356c20a84ec2abe7990a9aa42af5a9a9f851cb003687f?color=5a5a5a) Nach
Nach  Stunden zeigt die Balkenanzeige den ersten Balken.
In Abbildung 1 lässt sich erkennen, dass die Graphen von
Stunden zeigt die Balkenanzeige den ersten Balken.
In Abbildung 1 lässt sich erkennen, dass die Graphen von  mit größer werdenden Werten von
mit größer werdenden Werten von  immer weniger stark ansteigen, da sie sich der Asymptote
immer weniger stark ansteigen, da sie sich der Asymptote  annähern.
annähern.
Die Ladung des Akkus nimmt zu, je weiter der Akku schon geladen ist.
Da die Balken jeweils in einem konstanten Ladungsabstand von bzw.
bzw.  angezeigt werden, dauert es länger, bis der nächste Balken angezeigt wird.
angezeigt werden, dauert es länger, bis der nächste Balken angezeigt wird.
Die Ladung des Akkus nimmt zu, je weiter der Akku schon geladen ist.
Da die Balken jeweils in einem konstanten Ladungsabstand von
(3)
Je größer der Wert  ist, desto größer ist auch der Funktionswert
ist, desto größer ist auch der Funktionswert  an einer bestimmten Stelle
an einer bestimmten Stelle  Die Funktion steigt für einen größeren Wert von
Die Funktion steigt für einen größeren Wert von  folglich schneller an. Der Akku gewinnt dadurch schneller an Ladung und hat so schneller eine bestimmte Ladung erreicht.
folglich schneller an. Der Akku gewinnt dadurch schneller an Ladung und hat so schneller eine bestimmte Ladung erreicht.
Der Wert ist der drittgrößte der angegebenen Werte. Der Graph zu Ladegerät 3 gehört also zum Parameter
ist der drittgrößte der angegebenen Werte. Der Graph zu Ladegerät 3 gehört also zum Parameter 
Der Wert
b)
(1)
Der Ladestrom wird durch die Funktion  mit
mit  beschrieben.
beschrieben.
Für größer werdende Werte von wird
wird  immer kleiner, der Faktor
immer kleiner, der Faktor  bleibt dagegen konstant. Die Funktion
bleibt dagegen konstant. Die Funktion  ist für
ist für  streng monoton fallend. Der Ladestrom ist also immer zum Startzeitpunkt des Intervalls am größten.
streng monoton fallend. Der Ladestrom ist also immer zum Startzeitpunkt des Intervalls am größten.
Für größer werdende Werte von
(2)
(3)
c)
(1)
1. Schritt: Ableitungen bilden
Mit der Produkt- und der Kettenregel folgt:
![\(\begin{array}[t]{rll}
I_d(t) &=& (100t+50)\mathrm e^{-0,4\cdot t+0,1} \\[5pt]
I_d](https://mathjax.schullv.de/0b4749886d2309d1e54131825ade937a6cb2d0745bf156f7d8566958346c02e6?color=5a5a5a) 2. Schritt: Notwendiges Kriterium für Extremstellen anwenden
2. Schritt: Notwendiges Kriterium für Extremstellen anwenden
![\(\begin{array}[t]{rll}
I_d](https://mathjax.schullv.de/6a0ed8aae0dfbb3fabb825bec0ce647ff41df2d3c58473d4a12ce7ceb54ebcf5?color=5a5a5a) Die Funktion
Die Funktion  kann also höchstens ein lokales Maximum besitzen, da nur an der Stelle
kann also höchstens ein lokales Maximum besitzen, da nur an der Stelle  das notwendige Kriterium für lokale Extremstellen erfüllt ist.
3. Schritt: Hinreichendes Kriterium für Extremstellen anwenden
das notwendige Kriterium für lokale Extremstellen erfüllt ist.
3. Schritt: Hinreichendes Kriterium für Extremstellen anwenden
![\(\begin{array}[t]{rll}
I_d](https://mathjax.schullv.de/a18143d62a234e75e1f6f9df4ac64bd649c6c710896e9b57a51d3d96418b076f?color=5a5a5a) An der einzigen Stelle, an der das notwendige Kriterium für ein lokales Extremum erfüllt ist, besitzt
An der einzigen Stelle, an der das notwendige Kriterium für ein lokales Extremum erfüllt ist, besitzt  also ein Maximum.
also ein Maximum.  besitzt daher genau ein lokales Maximum.
besitzt daher genau ein lokales Maximum.
(2)
An der Stelle  hat
hat  laut d) (1) ein lokales Maximum. Der Funktionswert beträgt dort:
laut d) (1) ein lokales Maximum. Der Funktionswert beträgt dort:
 Da dies die einzige lokale Extremstelle von
Da dies die einzige lokale Extremstelle von  ist, kann es keine Randextrema geben. Der maximale Wert, den der Ladestrom annimmt, ist daher
ist, kann es keine Randextrema geben. Der maximale Wert, den der Ladestrom annimmt, ist daher  Er kann also den Wert
Er kann also den Wert  nie überschreiten.
nie überschreiten.
d)
(1)
Der Zeitpunkt  ist der Zeitpunkt, an dem der konstante Ladestrom mit
ist der Zeitpunkt, an dem der konstante Ladestrom mit  in den Ladestrom
in den Ladestrom  wechselt. Dies passiert, wenn die Ladung des Akkus
wechselt. Dies passiert, wenn die Ladung des Akkus  beträgt.
beträgt.
 Nach
Nach  Stunden hat der Akku also eine Ladung von
Stunden hat der Akku also eine Ladung von  erreicht und wechselt in den Ladestrom, der durch die Funktion
erreicht und wechselt in den Ladestrom, der durch die Funktion  beschrieben wird. Der Ladevorgang bricht dann ab, wenn dieser den Wert
beschrieben wird. Der Ladevorgang bricht dann ab, wenn dieser den Wert  erreicht.
erreicht.
![\(\begin{array}[t]{rll}
I(t_2)&=& 10 \\[5pt]
500\mathrm e^{-5(t_2-t_1)} &=& 10 \\[5pt]
500\mathrm e^{-5(t_2-1,8)} &=& 10 &\quad \scriptsize \mid\; :500\\[5pt]
\mathrm e^{-5(t_2-1,8)} &=& 0,02 &\quad \scriptsize \mid\;\ln \\[5pt]
-5(t_2-1,8)&=& \ln 0,02 &\quad \scriptsize \mid\; :-5 \\[5pt]
t_2-1,8&=& -\frac{\ln 0,02}{5} &\quad \scriptsize \mid\; :+1,8 \\[5pt]
t_2&=& -\frac{\ln 0,02}{5} +1,8\\[5pt]
&\approx& 2,58\\[5pt]
\end{array}\)](https://mathjax.schullv.de/36f81c32893ac36aee715614c0cc3673bb194d575fe6f8e18d5e13f09b318dfc?color=5a5a5a) Der Ladevorgang dauert ca.
Der Ladevorgang dauert ca.  Stunden.
Stunden.
(2)
Bekannt ist bereits, dass die Ladung des Akkus zum Zeitpunkt 
 beträgt. Es muss also noch die Ladung berechnet werden, die von
beträgt. Es muss also noch die Ladung berechnet werden, die von  bis
bis  dazukommt. Diese kann mit einem Integral über
dazukommt. Diese kann mit einem Integral über  berechnet werden. Der Wert des Integrals wird mit dem GTR bestimmt:
berechnet werden. Der Wert des Integrals wird mit dem GTR bestimmt:
 TI 84-PLUS
TI 84-PLUS
 Casio fx-CG
Am Ende des Ladevorgangs beträgt die Ladung also ca.
Casio fx-CG
Am Ende des Ladevorgangs beträgt die Ladung also ca. 
2nd  trace (calc)
trace (calc)  7:
7: 
F5 (G-Solv)  F6
F6  F3:
F3: 