Analysis 2
Gegeben ist die auf 
definierte Funktion 
mit 
.
Im Küstenschutz ist ein neuer Deich von Bedeutung: der Klimadeich. Der Querschnitt eines Klimadeichs wird durch die von dem Graphen der Funktion und der 
-Achse eingeschlossene Fläche modelliert. Dabei werden und 
in Metern 
angegeben.
an jeder Stelle eine vertikale Dicke von 
Der obere Rand des Querschnitts des Klimadeichs wird weiterhin durch beschrieben.
Gegeben ist die auf
definierte Funktionenschar 
mit 
.
Die Graphen von sollen für und 
den oberen Rand des Querschnitts des Sandkerns beschreiben.
Im Küstenschutz ist ein neuer Deich von Bedeutung: der Klimadeich. Der Querschnitt eines Klimadeichs wird durch die von dem Graphen der Funktion
a)
Die Abbildung zeigt den Graphen von . Markiere auf der -Achse das Intervall, in dem der Klimadeich mindestens 
hoch ist. Ein moderner Deich ist etwa fünfmal so breit wie er hoch ist. Entscheide, ob der Klimadeich diese Regel erfüllt. Begründe deine Entscheidung nur mit Hilfe der Abbildung.
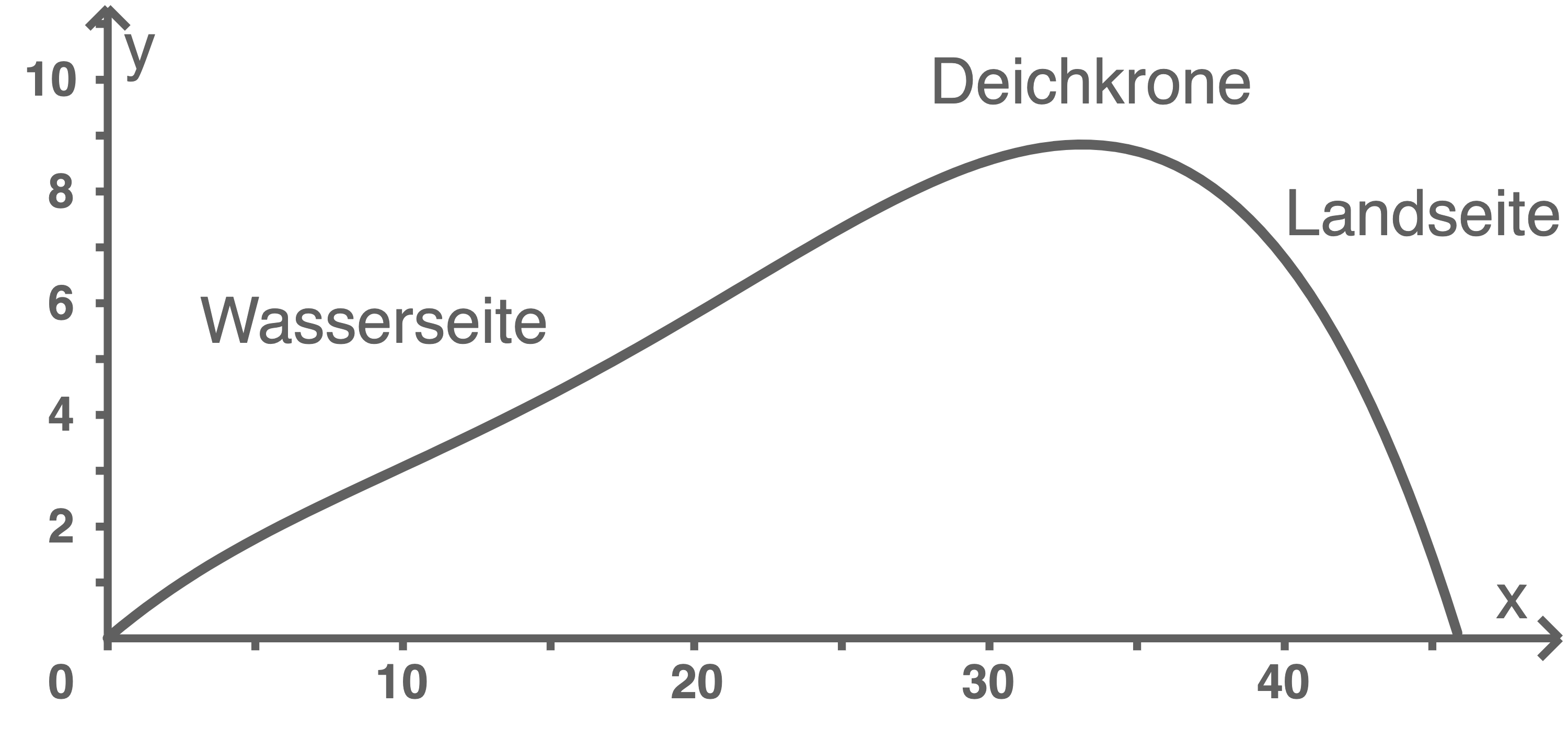
(3 Punkte)
b)
Die maximale Höhe des Klimadeichs ist 
höher als die des zuvor vorhandenen Deiches.
Berechne die maximale Höhe des früheren Deiches auf
genau.
Berechne die maximale Höhe des früheren Deiches auf
(4 Punkte)
c)
Berechne die durchschnittliche Steigung des Klimadeiches im Intervall ![\([0;30].\)](https://mathjax.schullv.de/ade4525d56dd628cc4fb46c822c7f7aeb3403a9ad2d38e0ae0ef0c41ddf0fd73?color=5a5a5a)
Berechne den Neigungswinkel des Klimadeichs an der Stelle
.
Der Klimadeich besteht aus einem Sandkern und einer Abdeckungsschicht aus Kleiboden. Im Querschnitt hat die Abdeckungsschicht aus Kleiboden im Bereich Berechne den Neigungswinkel des Klimadeichs an der Stelle
(5 Punkte)
d)
Erstelle eine Hilfsskizze.
(3 Punkte)
e)
Berechne den prozentualen Anteil des Sandkerns im Querschnitt im Bereich 
(5 Punkte)
f)
Begründe, dass im Bereich von 
bis 
mit 
der Inhalt des Querschnitts der Kleibodenschicht mit 
berechnet werden kann.
(4 Punkte)
g)
An der Stelle 
wird senkrecht zum oberen Rand des Querschnitts eine geradlinige Bohrung durchgeführt.
Berechne die Koordinaten des Punktes, in dem diese Bohrung den Sandkern erreicht.
Der obere Rand des Querschnitts des Sandkerns wird neu modelliert.
Berechne die Koordinaten des Punktes, in dem diese Bohrung den Sandkern erreicht.
(5 Punkte)
Der obere Rand des Querschnitts des Klimadeichs wird weiterhin durch
Gegeben ist die auf
Die Graphen von
h)
In der Abbildung sind die Graphen von zwei Vertretern von abgebildet. Gib für den Graph I und Graph II jeweils einen Näherungswert für 
an.
Begründe deine Angaben.
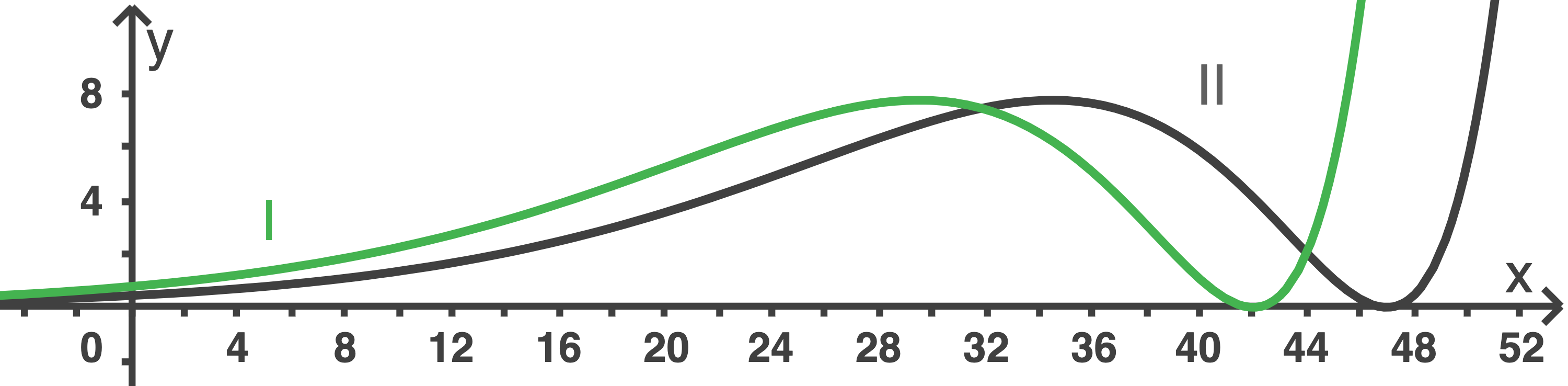
Begründe deine Angaben.
(4 Punkte)
i)
Die vertikale Dicke der Abdeckungsschicht aus Kleiboden soll
mit gibt, sodass beide Bedingungen gleichzeitig erfüllt sind.
an der Stelle
betragen und
- im Querschnitt im Bereich
betragen.
(7 Punkte)
(40 Punkte)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
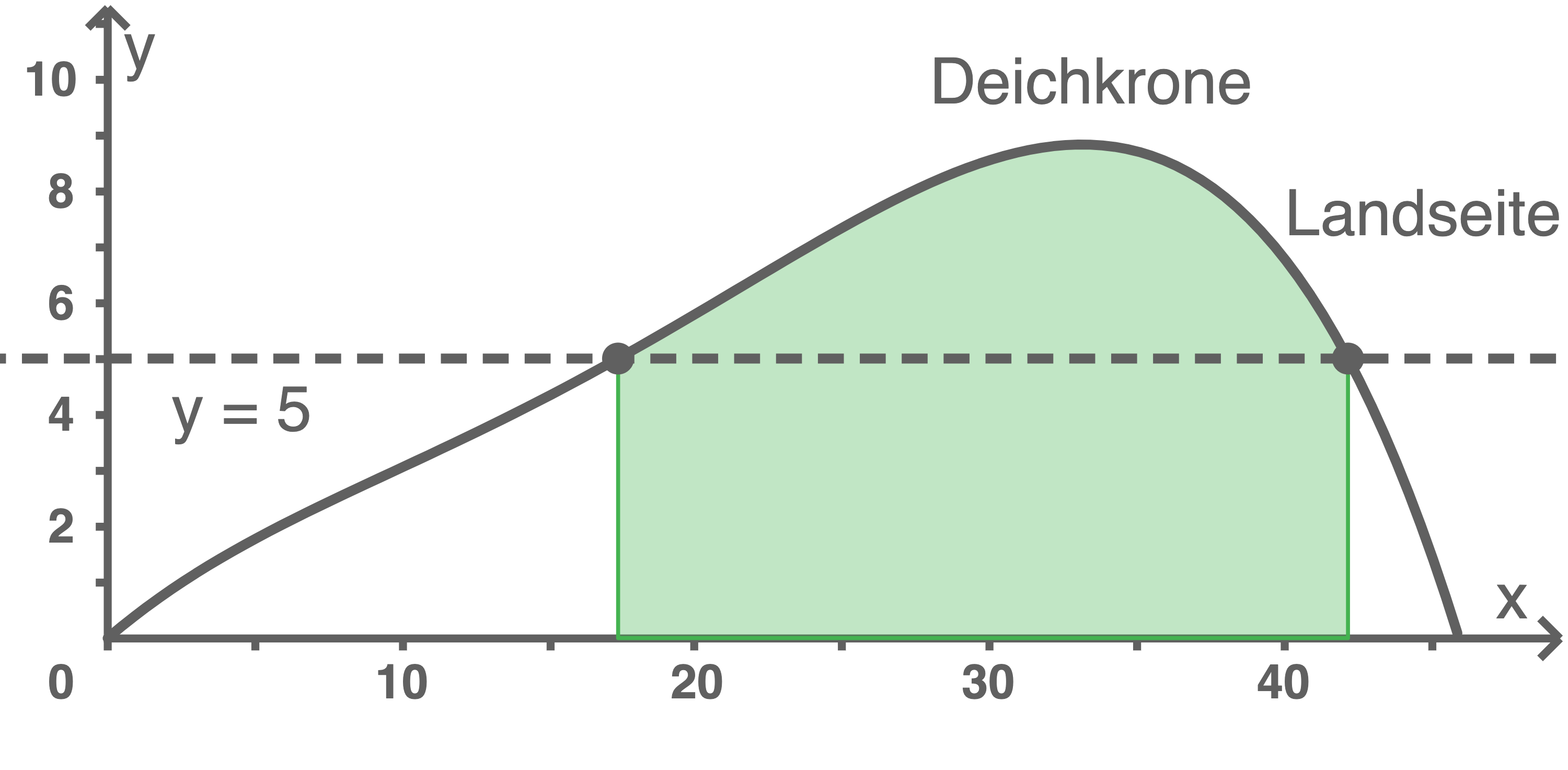
Es gilt
b)
Die 
-Koordinaten des Hochpunktes von geben die maximale Höhe des Klimadeichs an.
Es gilt:
Mit dem solve-Befehl des GTRs ergibt sich 
Auf die hinreichende Bedingung für Extremstellen kann verzichtet werden, da in der Aufgabenstellung gegeben ist, dass die maximale Höhe existiert. 
entspricht der -Koordinate des Hochpunktes.
Die maximale Höhe des Klimadeichs folgt mit:
Die Höhe des früheren Deiches ergibt sich zu 
c)
Durchschnittliche Steigung
Es ist 
und 
Die durchschnittliche Steigung im Intervall ![\([0;30]\)](https://mathjax.schullv.de/0341dfdd40253008b25ebe392a4b96edf71ca0e72677779399230fd16f9b7720?color=5a5a5a)
ist gegeben durch ![\(\dfrac{8,55-0}{30-0}=\dfrac{8,55}{30}=0,285 \;\text{[m]}.\)](https://mathjax.schullv.de/c095fdbdef64cfc7792f8c5353b16f72ea26d502c57c6ebe018259d24701c7a0?color=5a5a5a)
Neigungswinkel berechnen
Es gilt 
Steigung an der Stelle berechnen:
Der Neigungswinkel ergibt sich mit:
![\(\begin{array}[t]{rll}
\tan(\alpha)&=& 0,45&\quad \scriptsize \mid\; \tan^{-1} \\[5pt]
\alpha&\approx& 24,2^{\circ}
\end{array}\)](https://mathjax.schullv.de/5a36119d37bc079c2bca65a7d6c3de37ed97925f70b30d59c53d4735b9b9fe8b?color=5a5a5a)
d)
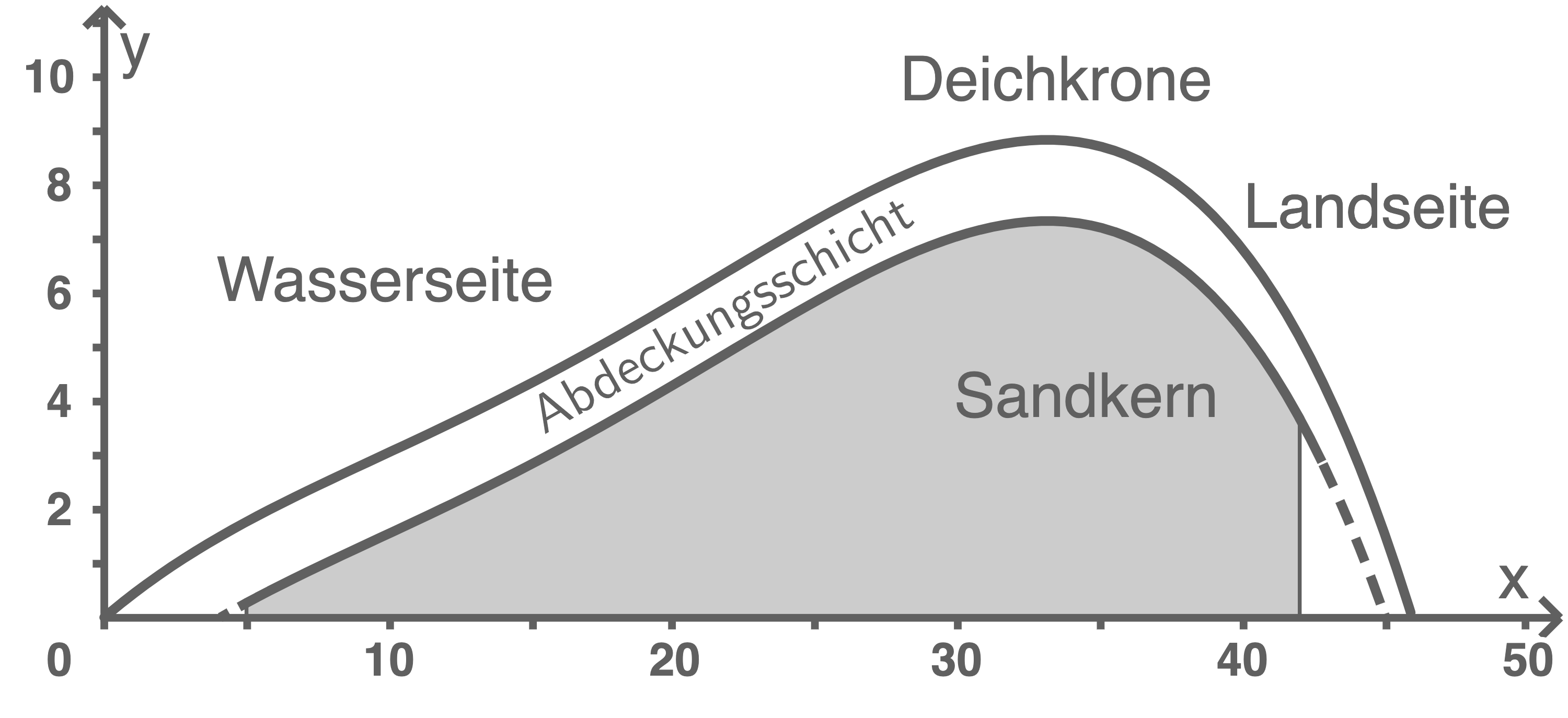
e)
1. Schritt: Inhalt der Querschnittsfläche bestimmen
Der Inhalt der Querschnittsfläche im Intervall ![\([5;42]\)](https://mathjax.schullv.de/d4c23eaef0d15108722382d7f930c3f812528fb359ffd6f9c7fa410c50eec359?color=5a5a5a)
ergibt sich mit:
2. Schritt: Inhalt der Fläche des Sandkernquerschnitts bestimmen
Der obere Randverlauf des Sandkerns wird durch die Funktion 
beschrieben.
Der Inhalt der Fläche des Sandkernquerschnitts im gesuchten Intervall folgt mit:
3. Schritt: Prozentualen Anteil bestimmen
![\(\dfrac{168,87\;\text{[m]}^2}{224,37\;\text{[m]}^2}\approx 0,75=75\%.\)](https://mathjax.schullv.de/817f4fa586b0cfc884560c6d05d74fea045200beb4e16731c4aa6ad66b6eeefc?color=5a5a5a)
f)
Der untere Randverlauf der Kleibodenschicht wird durch die Funktion 
beschrieben.
Der Flächeninhalt des Querschnitts der Kleibodenschicht im Bereich 
ist damit gegeben durch
g)
1. Schritt: Normale an die Funktion an der Stelle berechnen
Es gilt 
Damit ist die Normalengleichung an im Punkt 
an gegeben durch
2. Schritt: Abstand berechnen Die Stelle, an der die Normale die Funktion schneidet, ist gegeben durch die Lösung der Gleichung 
Mit dem GTR folgt: Der Schnittpunkt im gesuchten Intervall befindet sich an der Stelle 
Die Normale an im Punkt schneidet die obere Grenze des Sandkerns im Punkt 
2. Schritt: Abstand berechnen Die Stelle, an der die Normale die Funktion
Die Normale an
h)
Der Funktion kann entnommen werden, dass sich an der Stelle eine doppelte Nullstelle und damit eine Berührstelle des Graphen mit der 
Achse befindet.
Die Graphen 
und 
berühren die Achse an den Stellen 
und 
Dies sind damit die gesuchten Werte für 
i)
Die erste Bedingung liefert die Gleichung 
Die Gleichung im relevanten Bereich wird mit dem GTR gelöst und hat die Lösung 
Für die zweite Bedingung muss zusätzlich 
erfüllt sein.
Beispielsweise an der Stelle
gilt jedoch 
Damit können für keinen Wert von aus dem gegebenen Intervall beide Bedingungen gleichzeitig erfüllt sein.
Beispielsweise an der Stelle