Aufgabe 2
In ein Staubecken oberhalb eines Bergdorfes fließen zwei Bäche. Nach Regenfällen unterschiedlicher Dauer und Stärke können die momentanen 1 Zuflusssraten aus den beiden Bächen durch Funktionen  für den Bach 1 und
für den Bach 1 und  für den Bach 2 und die Gesamtzuflussrate aus den beiden Bächen durch eine Funktion
für den Bach 2 und die Gesamtzuflussrate aus den beiden Bächen durch eine Funktion  für einen bestimmten Beobachtungszeitraum modelliert werden. Gegeben sind für
für einen bestimmten Beobachtungszeitraum modelliert werden. Gegeben sind für  zunächst die Funktionsgleichungen
zunächst die Funktionsgleichungen

 Dabei fasst man
Dabei fasst man  als Maßzahl zur Einheit 1 h und
als Maßzahl zur Einheit 1 h und  ,
,  sowie
sowie  als Maßzahlen zur Einheit 1
als Maßzahlen zur Einheit 1  auf. Der Beobachtungszeitraum beginnt zum Zeitpunkt
auf. Der Beobachtungszeitraum beginnt zum Zeitpunkt  und endet zum Zeitpunkt
und endet zum Zeitpunkt  . Die Graphen von
. Die Graphen von  ,
,  und
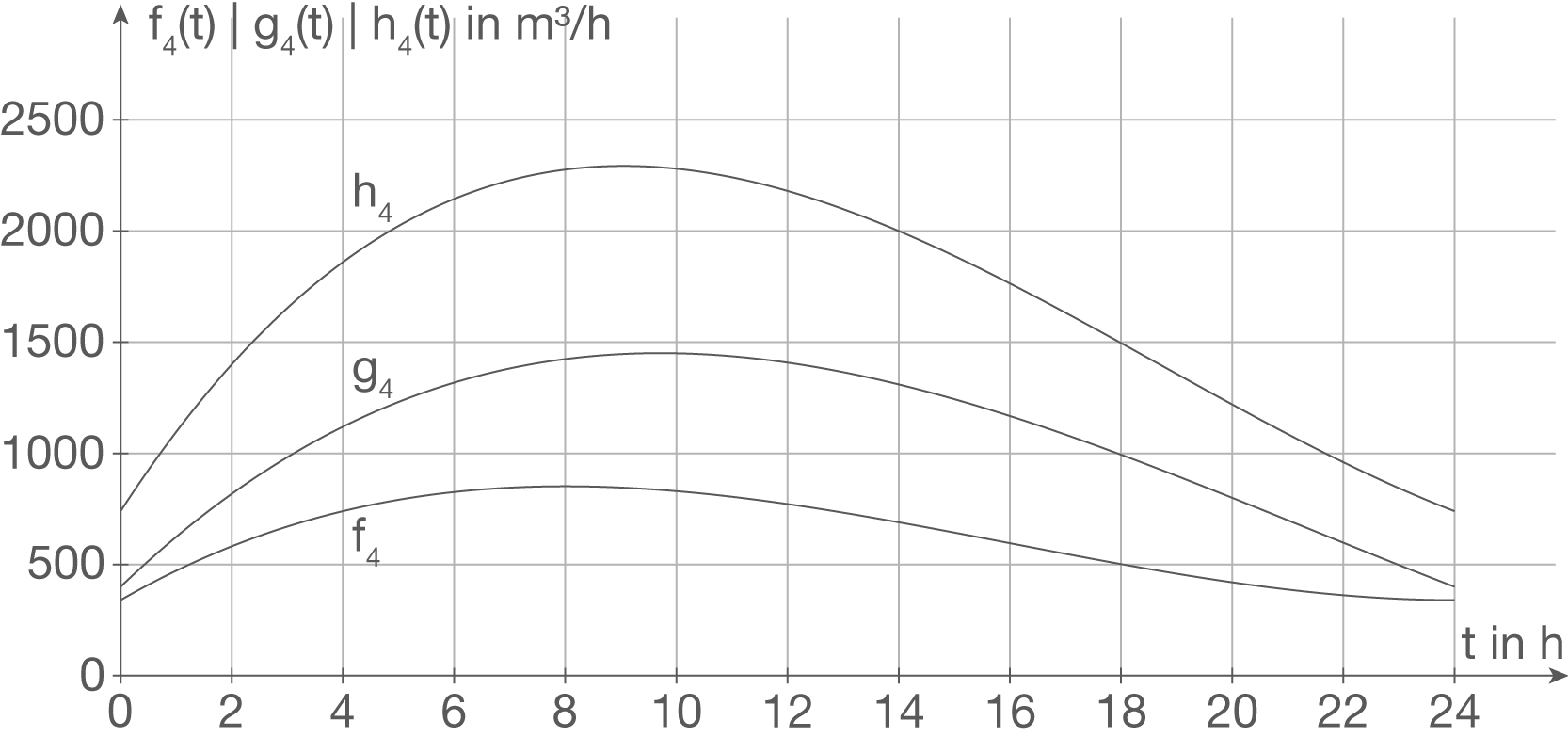
und  sind in der Abbildung dargestellt.
sind in der Abbildung dargestellt.
1Im Folgenden wird zur besseren Lesbarkeit nur der Begriff Zuflussrate verwendet; darunter ist stets die momentane Zuflussrate zu verstehen
a)
- Berechnen Sie die Gesamtzuflussrate aus den beiden Bächen zu Beginn und am Ende des Beobachtungszeitraums.
- Zeigen Sie, dass für die Funktion
, die die Zuflussrate aus Bach 2 beschreibt, gilt:\vspace{.2cm}
.
- Begründen Sie, dass unabhängig vom Parameter
die Zuflussrate aus Bach 2 für alle
größer ist als die Zuflussrate aus Bach 1.
- Bestimmen Sie in Abhängigkeit von
den Zeitpunkt
, zu dem die Gesamtzuflussrate ihr Maximum annimmt.
(3P + 2P + 8P + 8P)
b)
- Bestimmen Sie die Wendestelle der Funktion
.
- Bestimmen Sie den Zeitpunkt des Beobachtungszeitraums, zu dem sich die Gesamtzulaufrate am stärksten ändert.
- Geben Sie nun die Bedeutung der Wendestelle aus (1) im Sachzusammenhang an.
(6P + 6P + 3P)
c)
Im Folgenden sei ![\(a=4:h_{4}(t)=\frac{1}{2}t^{3}-28t^{2}+384t+740, t\in[0;24].\)](https://mathjax.schullv.de/7e82004dd6336d51877cd8dfcc408aa9f5b6856d55bc34b152c4f7838ad429d7?color=5a5a5a)
Zum Zeitpunkt kann das Staubecken noch 20.000m
kann das Staubecken noch 20.000m Wasser aufnehmen.
Wasser aufnehmen.
Zum Zeitpunkt
- Entscheiden Sie, ob das Staubecken das gesamte Wasser aus den beiden Bächen während der 24 Stunden des Beobachtungszeitraums aufnehmen könnte.
- Die Gleichung
hat die (positive) Lösung
Geben Sie die Bedeutung dieser Lösung im Sachzusammenhang an. - Um ein Überlaufen des Staubeckens zu verhindern, wird zum Zeitpunkt
ein vorher verschlossener Notablauf geöffnet. Durch diesen fließt Wasser mit einer konstanten Abflussrate von
aus dem Staubecken ab. Der Notablauf bleibt bis zum Ende des Beobachtungszeitraums geöffnet. Ohne Nachweis darf verwendet werden, dass die Gesamtzuflussrate für
größer und für
kleiner als
ist (vgl. Abbildung auf Seite 4).
Untersuchen Sie, ob das Staubecken innerhalb des Beobachtungszeitraums überläuft.
(4P + 2P + 8P)
a) (1)
 Berechnen der Gesamtzuflussrate zu Beginn und am Ende der Beobachtung
Der Aufgabenstellung kannst du entnehmen, dass in ein Staubecken zwei Bäche hineinfließen. Nach Regenfällen unterschiedlicher Dauer und Stärke können die momentanen Zuflussraten aus den beiden Bächen durch die Funktion
Berechnen der Gesamtzuflussrate zu Beginn und am Ende der Beobachtung
Der Aufgabenstellung kannst du entnehmen, dass in ein Staubecken zwei Bäche hineinfließen. Nach Regenfällen unterschiedlicher Dauer und Stärke können die momentanen Zuflussraten aus den beiden Bächen durch die Funktion  für Bach 1 und
für Bach 1 und  für Bach 2 für einen bestimmten Beobachtungszeitraum modelliert werden. Die Gesamtzuflussrate aus den beiden Bächen wird durch die Funktion
für Bach 2 für einen bestimmten Beobachtungszeitraum modelliert werden. Die Gesamtzuflussrate aus den beiden Bächen wird durch die Funktion  beschrieben.
beschrieben.
Die Funktionen und
und  sind für
sind für  und
und  wie folgt angegeben:
wie folgt angegeben:
 ist dabei in Stunden (h) angegeben. Die Funktionswerte
ist dabei in Stunden (h) angegeben. Die Funktionswerte  ,
,  und
und  beschreiben die Zuflussrate in
beschreiben die Zuflussrate in  . Der Beobachtungszeitraum beginnt beim Zeitpunkt
. Der Beobachtungszeitraum beginnt beim Zeitpunkt  und endet zum Zeitpunkt
und endet zum Zeitpunkt  .
.
Deine Aufgabe ist es nun, die Gesamtzuflussrate zu Beginn und am Ende des Beobachtungszeitraums zu bestimmen. Zu betrachten ist hier also Funktion , da diese die Gesamtzuflussrate in das Staubecken beschreibt. Von oben weißt du, dass die Beobachtung zum Zeitpunkt
, da diese die Gesamtzuflussrate in das Staubecken beschreibt. Von oben weißt du, dass die Beobachtung zum Zeitpunkt  startet und am Zeitpunkt
startet und am Zeitpunkt  endet.
endet.
Willst du diese Aufgabe lösen, so berechnest du die Funktionswerte von an diesen Zeitpunkten.
Gesamtzuflussrate am Beobachtungsbeginn
an diesen Zeitpunkten.
Gesamtzuflussrate am Beobachtungsbeginn  :
:
 .
Gesamtzuflussrate am Beobachtungsende
.
Gesamtzuflussrate am Beobachtungsende  :
:
 Die Gesamtzuflussrate ist zu Beginn und am Ende des Beobachtungszeitraums
Die Gesamtzuflussrate ist zu Beginn und am Ende des Beobachtungszeitraums  .
.
Die Funktionen
Deine Aufgabe ist es nun, die Gesamtzuflussrate zu Beginn und am Ende des Beobachtungszeitraums zu bestimmen. Zu betrachten ist hier also Funktion
Willst du diese Aufgabe lösen, so berechnest du die Funktionswerte von
(2)
 Zeigen, dass
Zeigen, dass  durch den Funktionsterm
durch den Funktionsterm  dargestellt werden kann
Nun sollst du zeigen, dass der Funktionsterm der Funktion
dargestellt werden kann
Nun sollst du zeigen, dass der Funktionsterm der Funktion  , die die Zuflussrate von Bach 2 in das Staubecken repräsentiert, durch den folgenden Funktionsterm beschrieben werden kann:
, die die Zuflussrate von Bach 2 in das Staubecken repräsentiert, durch den folgenden Funktionsterm beschrieben werden kann:
Willst du diesen Sachverhalt zeigen, so musst du hier Funktion  betrachten. Diese beschreibt die Gesamtzuflussrate in das Staubecken. Da außer Bach 1, beschrieben durch
betrachten. Diese beschreibt die Gesamtzuflussrate in das Staubecken. Da außer Bach 1, beschrieben durch  und Bach 2, beschrieben durch
und Bach 2, beschrieben durch  , kein weiterer Fluss in das Staubecken fließt, ergibt sich die Gesamtzuflussrate aus der Summe der Zuflussraten von Bach 1 und Bach 2.
Für den Funktionsterm von
, kein weiterer Fluss in das Staubecken fließt, ergibt sich die Gesamtzuflussrate aus der Summe der Zuflussraten von Bach 1 und Bach 2.
Für den Funktionsterm von  gilt also:
gilt also:
 Stelle nach
Stelle nach  um und setze ein, um den Sachverhalt hier zu zeigen:
um und setze ein, um den Sachverhalt hier zu zeigen:
 Da der berechnete und der gegebene Funktionsterm übereinstimmen, hast du die Aufgabe hier richtig gelöst.
Da der berechnete und der gegebene Funktionsterm übereinstimmen, hast du die Aufgabe hier richtig gelöst.
|
|
(3)
 Begründen, dass Zuflussrate aus Bach 2 größer ist als die von Bach 1
Nun ist es deine Aufgabe, zu begründen, dass unabhängig von Parameter
Begründen, dass Zuflussrate aus Bach 2 größer ist als die von Bach 1
Nun ist es deine Aufgabe, zu begründen, dass unabhängig von Parameter  , die Zuflussrate aus Bach 2 für alle
, die Zuflussrate aus Bach 2 für alle ![\(t \in \left[0;6a\right]\)](https://mathjax.schullv.de/db6125b4f8e52a1658217cff72567d2917947e05036bef65c36029c955127c99?color=5a5a5a) größer ist als die Zuflussrate aus Bach 1. Willst du zeigen, dass die Zuflussrate von Bach 2 im gesamten Beobachtungszeitraum größer als die Zuflussrate von Bach 1 ist, so musst du zeigen, dass der Graph von
größer ist als die Zuflussrate aus Bach 1. Willst du zeigen, dass die Zuflussrate von Bach 2 im gesamten Beobachtungszeitraum größer als die Zuflussrate von Bach 1 ist, so musst du zeigen, dass der Graph von  innerhalb des Beobachtungszeitraums oberhalb des Graphen von
innerhalb des Beobachtungszeitraums oberhalb des Graphen von  verläuft.
verläuft.
Willst du dies begründen, so betrachtest du hier die Differenz zwischen dem Graphen von und
und  . Diese Differenz kann durch die Differenzfunktion
. Diese Differenz kann durch die Differenzfunktion  beschrieben werden, welche sich wie folgt berechnen lässt:
beschrieben werden, welche sich wie folgt berechnen lässt:
Willst du zeigen, dass die Zuflussrate aus Bach 2 immer größer ist als die Zuflussrate aus Bach 1, so zeigst du hier, dass die Differenz zwischen diesen Funktionen unabhängig von  immer größer gleich Null ist. Bezogen auf
immer größer gleich Null ist. Bezogen auf  und den Beobachtungszeitraum gilt also:
und den Beobachtungszeitraum gilt also:
Bilde also zunächst die Funktion  und zeige das Folgendes für diese gilt:
und zeige das Folgendes für diese gilt:
 Berechne die oben angegebene Differenz, um
Berechne die oben angegebene Differenz, um  zu erhalten:
zu erhalten:
 2. Schritt: Untersuchen der Randstellen des Intervalls
Zeige nun, durch Berechnen der Funktionswerte von
2. Schritt: Untersuchen der Randstellen des Intervalls
Zeige nun, durch Berechnen der Funktionswerte von  an den Randstellen
an den Randstellen  und
und  des Intervalls, dass
des Intervalls, dass  unabhängig von
unabhängig von  an diesen Stellen einen Wert größer Null annimmt:
an diesen Stellen einen Wert größer Null annimmt:

 So hast du also gezeigt, dass Funktion
So hast du also gezeigt, dass Funktion  an den Randstellen
an den Randstellen  und
und  des Intervalls unabhängig von
des Intervalls unabhängig von  , oberhalb der Funktion
, oberhalb der Funktion  verläuft.
3. Schritt: Untersuchen des Verhaltens des Graphen von
verläuft.
3. Schritt: Untersuchen des Verhaltens des Graphen von  im Intervall
Untersuche nun das Verhalten des Graphen von
im Intervall
Untersuche nun das Verhalten des Graphen von  innerhalb der Intervallsgrenzen. Um zu zeigen, dass
innerhalb der Intervallsgrenzen. Um zu zeigen, dass  im gesamten Intervall oberhalb von
im gesamten Intervall oberhalb von  verläuft, musst du hier zeigen, dass
verläuft, musst du hier zeigen, dass  innerhalb des Intervalls nur Werte größer Null annimmt.
innerhalb des Intervalls nur Werte größer Null annimmt.
Betrachte dazu den Funktionsterm von :
:
 Da
Da  gilt, handelt es sich hier um eine nach unten geöffnete Parabel. Da diese an den Randstellen
gilt, handelt es sich hier um eine nach unten geöffnete Parabel. Da diese an den Randstellen  und
und  unabhängig von
unabhängig von  Werte größer Null annimmt, muss diese im Intervall
Werte größer Null annimmt, muss diese im Intervall ![\(\left[0;6 \cdot a\right]\)](https://mathjax.schullv.de/e02627b3d24cbaf4002540ab999a6efcd4f13a153ed93465efc9c596c81ef1af?color=5a5a5a) oberhalb der
oberhalb der  -Achse verlaufen. Da die Differenz zwischen
-Achse verlaufen. Da die Differenz zwischen  und
und  im betrachteten Intervall unabhängig von
im betrachteten Intervall unabhängig von  größer Null ist, hast du gezeigt, dass die Zuflussrate von Bach 2 im gesamt betrachteten Zeitraum größer als die Zuflussrate von Bach 1 ist.
größer Null ist, hast du gezeigt, dass die Zuflussrate von Bach 2 im gesamt betrachteten Zeitraum größer als die Zuflussrate von Bach 1 ist.
Willst du dies begründen, so betrachtest du hier die Differenz zwischen dem Graphen von
|
|
|
|
- Zeige, dass
an den Randstellen des betrachteten Intervalls Werte größer Null annimmt.
- Zeige, der Graph von
zwischen den Randstellen oberhalb der
-Achse verläuft.
Betrachte dazu den Funktionsterm von
(4)
 Bestimmen des Zeitpunkts, an dem die Gesamtzuflussrate maximal ist
Zuletzt sollst du hier jenen Zeitpunkt im Beobachtungszeitraum bestimmen, bei dem die Gesamtzuflussrate ihr Maximum annimmt. Du untersuchst also
Bestimmen des Zeitpunkts, an dem die Gesamtzuflussrate maximal ist
Zuletzt sollst du hier jenen Zeitpunkt im Beobachtungszeitraum bestimmen, bei dem die Gesamtzuflussrate ihr Maximum annimmt. Du untersuchst also  auf Maximalstellen.
auf Maximalstellen.
Du weißt, an einer bestimmten Stelle liegt genau dann ein Maximum vor, wenn folgende Bedingungen an dieser erfüllt sind:
liegt genau dann ein Maximum vor, wenn folgende Bedingungen an dieser erfüllt sind:
 und ermittle über Auswerten der oben gegebenen Bedingungen die gesuchte Maximalstelle im Intervall.
und ermittle über Auswerten der oben gegebenen Bedingungen die gesuchte Maximalstelle im Intervall.
Da hier aber ein abgeschlossenes Intervall angegeben ist, musst du hier die Randstellen von und
und  untersuchen, um das globale Maximum im gegebenen Intervall zu ermitteln. Vergleiche dazu die Funktionswerte von
untersuchen, um das globale Maximum im gegebenen Intervall zu ermitteln. Vergleiche dazu die Funktionswerte von  an den Randstellen und beim ermittelten Maximum.
an den Randstellen und beim ermittelten Maximum.
Gehe beim Lösen der Aufgabe also so vor: und
und  ergibt sich hier:
ergibt sich hier:

 2. Schritt: Maximalstellen von
2. Schritt: Maximalstellen von  bestimmen
Bestimme zunächst die Nullstellen von
bestimmen
Bestimme zunächst die Nullstellen von  , um die potentiellen Extremstellen von
, um die potentiellen Extremstellen von  in Abhängigkeit von
in Abhängigkeit von  zu bestimmen:
zu bestimmen:
 Hier liegt eine quadratische Gleichung löse diese mit Hilfe der
Hier liegt eine quadratische Gleichung löse diese mit Hilfe der  -
- - oder der Mitternachtsformel.
- oder der Mitternachtsformel.
 -
- -Formel:
-Formel:
 Mitternachtsformel:
Mitternachtsformel:
 Als potentielle Extremstellen ergeben sich also
Als potentielle Extremstellen ergeben sich also  und
und  . Da für
. Da für 

gilt und diese Extremstelle damit nicht mehr im betrachteten Intervall liegt, wird hier im Folgenden nur noch betrachtet.
Überprüfe nun die hinreichende Bedingung bei
betrachtet.
Überprüfe nun die hinreichende Bedingung bei  , um festzustellen, ob an dieser Stelle eine Maximalstelle vorliegt. Beachte dabei, dass auch hier
, um festzustellen, ob an dieser Stelle eine Maximalstelle vorliegt. Beachte dabei, dass auch hier  gilt.
gilt.
 Bei
Bei  liegt also eine Maximalstelle der Funktion
liegt also eine Maximalstelle der Funktion  vor.
3. Schritt: Überprüfen der Randstellen des Intervalls
Im ersten Aufgabenteil dieser Teilaufgabe hast du bestimmt, dass für die Funktionswerte von
vor.
3. Schritt: Überprüfen der Randstellen des Intervalls
Im ersten Aufgabenteil dieser Teilaufgabe hast du bestimmt, dass für die Funktionswerte von  an den Randstellen, unabhängig von
an den Randstellen, unabhängig von  , folgendes gilt:
, folgendes gilt:
 .
Überprüfe nun den Funktionswert bei
.
Überprüfe nun den Funktionswert bei  , um zu überprüfen, ob an dieser Stelle auch ein globales Maximum vorliegt:
, um zu überprüfen, ob an dieser Stelle auch ein globales Maximum vorliegt:
 Da
Da  gilt, gilt
gilt, gilt  und
und  weshalb bei
weshalb bei  ein globales Maximum vorliegt.
ein globales Maximum vorliegt.
Die hier gesuchte Maximalstelle liegt also bei . Weiterhin wurde gezeigt, dass dieses Maximum ein globales ist.
. Weiterhin wurde gezeigt, dass dieses Maximum ein globales ist.
Du weißt, an einer bestimmten Stelle
- Notwendige Bedingung:
- Hinreichende Bedingung:
Da hier aber ein abgeschlossenes Intervall angegeben ist, musst du hier die Randstellen von
Gehe beim Lösen der Aufgabe also so vor:
- Bestimme die benötigten Ableitungsfunktionen
und
.
- Bestimme über die notwendige und hinreichende Bedingung die Maximalstellen von
.
- Untersuche die Funktionswerte an den Rand- und Maximalstellen.
gilt und diese Extremstelle damit nicht mehr im betrachteten Intervall liegt, wird hier im Folgenden nur noch
Die hier gesuchte Maximalstelle liegt also bei
b) (1)
 Bestimmen der Wendestelle von
Bestimmen der Wendestelle von  Hier ist es deine Aufgabe die Wendestelle der Funktion
Hier ist es deine Aufgabe die Wendestelle der Funktion  zu bestimmen. Da eine Wendestelle einem Extremum der ersten Ableitung der betrachteten Funktion entspricht, müssen hier die ersten drei Ableitungen von
zu bestimmen. Da eine Wendestelle einem Extremum der ersten Ableitung der betrachteten Funktion entspricht, müssen hier die ersten drei Ableitungen von  betrachtet werden.
betrachtet werden.
Beachte dabei, dass du die ersten beiden Ableitungen und
und  bereits im vorhergegangenen Aufgabenteil bestimmt hast. Liegt dann an einer bestimmten Stelle
bereits im vorhergegangenen Aufgabenteil bestimmt hast. Liegt dann an einer bestimmten Stelle  von
von  eine Wendestelle vor, so sind an dieser Stelle folgende Bedingungen erfüllt:
eine Wendestelle vor, so sind an dieser Stelle folgende Bedingungen erfüllt:
 zu bestimmen.
1. Schritt: Bestimmen der dritten Ableitungsfunktion von
zu bestimmen.
1. Schritt: Bestimmen der dritten Ableitungsfunktion von  1cm
Mit Hilfe der zweiten Ableitungsfunktion von
1cm
Mit Hilfe der zweiten Ableitungsfunktion von  , welche du im vorherigen Aufgabenteil bestimmt hast, ergibt sich
, welche du im vorherigen Aufgabenteil bestimmt hast, ergibt sich  zu:
zu:
 2. Schritt: Bestimmen der Wendestelle von
2. Schritt: Bestimmen der Wendestelle von  Bestimme nun die Wendestelle von
Bestimme nun die Wendestelle von  , indem du zunächst die Nullstellen (notwendige Bedingung) von
, indem du zunächst die Nullstellen (notwendige Bedingung) von  bestimmst:
bestimmst:
 Da für
Da für  :
:

für alle gilt, liegt eine Wendestelle der Funktion
gilt, liegt eine Wendestelle der Funktion  bei
bei  vor.
vor.
Beachte dabei, dass du die ersten beiden Ableitungen
- Notwendige Bedingung:
- Hinreichende Bedingung:
für alle
(2) + (3)
 Zeitpunkt an dem sich die Gesamtzuflussrate am stärksten ändert
Nun sollst du jenen Zeitpunkt im Beobachtungszeitraums bestimmen, zu dem sich die Gesamtzuflussrate am stärksten ändert. Der Zeitpunkt, an dem sich die Gesamtzuflussrate am stärksten ändert ist ein Punkt mit extremaler Steigung.
Rein intuitiv würde man sagen, dieser Punkt ist schon gefunden und entspricht dem Wendepunkt der Funktion
Zeitpunkt an dem sich die Gesamtzuflussrate am stärksten ändert
Nun sollst du jenen Zeitpunkt im Beobachtungszeitraums bestimmen, zu dem sich die Gesamtzuflussrate am stärksten ändert. Der Zeitpunkt, an dem sich die Gesamtzuflussrate am stärksten ändert ist ein Punkt mit extremaler Steigung.
Rein intuitiv würde man sagen, dieser Punkt ist schon gefunden und entspricht dem Wendepunkt der Funktion  . Da
. Da  hier jedoch auf einem abgeschlossenen Intervall untersucht wird, müssen hier, wie auch schon zu vor, die Randstellen des Intervalls untersucht werden.
hier jedoch auf einem abgeschlossenen Intervall untersucht wird, müssen hier, wie auch schon zu vor, die Randstellen des Intervalls untersucht werden.
Willst du also die den Zeitpunkt bestimmen, an dem sich die Gesamtzuflussrate im Zeitraum am stärksten ändert, so gehe hier so vor: ,
,  und
und  in
in  ein, um die Steigung der Gesamtzuflussraten an diesen Zeitpunkten zu bestimmen:
ein, um die Steigung der Gesamtzuflussraten an diesen Zeitpunkten zu bestimmen:
 2. Schritt: Bestimmen der Stelle mit betragsmäßig größter Steigung
Um nun die Stelle mit der betragsmäßig größten Steigung zu berechnen, musst du dir die oben berechneten Steigungen noch einmal etwas genauer ansehen. Du siehst, dass die Steigung an der Wendestelle
2. Schritt: Bestimmen der Stelle mit betragsmäßig größter Steigung
Um nun die Stelle mit der betragsmäßig größten Steigung zu berechnen, musst du dir die oben berechneten Steigungen noch einmal etwas genauer ansehen. Du siehst, dass die Steigung an der Wendestelle  für jedes
für jedes  betragsmäßig kleiner ist wie die Steigungen bei
betragsmäßig kleiner ist wie die Steigungen bei  . Die Steigung bei
. Die Steigung bei  ist sogar betragsmäßig kleiner als bei
ist sogar betragsmäßig kleiner als bei  und
und  .
.
Es folgt also, dass für der Zeitpunkt an dem sich die Gesamtzuflussrate am stärksten ändert bei
der Zeitpunkt an dem sich die Gesamtzuflussrate am stärksten ändert bei  liegt.
liegt.
 Bedeutung der Wendestelle aus (1) im Zusammenhang angeben
Der Zeitpunkt an dem sich die Gesamtzuflussrate lokal am stärksten ändert ist der Wendepunkt. Das heißt dieser Zeitpunkt liegt bei
Bedeutung der Wendestelle aus (1) im Zusammenhang angeben
Der Zeitpunkt an dem sich die Gesamtzuflussrate lokal am stärksten ändert ist der Wendepunkt. Das heißt dieser Zeitpunkt liegt bei  vor, mit
vor, mit  . Die Wendestelle entspricht also jener Stelle, an dem sich die Gesamtzuflussrate lokal am stärksten innerhalb des Betrachtungszeitraums
. Die Wendestelle entspricht also jener Stelle, an dem sich die Gesamtzuflussrate lokal am stärksten innerhalb des Betrachtungszeitraums  ändert.
ändert.
Willst du also die den Zeitpunkt bestimmen, an dem sich die Gesamtzuflussrate im Zeitraum am stärksten ändert, so gehe hier so vor:
- Bestimme die Steigung im Wendepunkt
- Bestimme die Steigung an den Randstellen
und
- Vergleiche die Steigungen und bestimme das globale Extremum der Steigung. Diese liegt dann in dem Punkt, mit dem betragsmäßig größten Steigung
Es folgt also, dass für
c) (1)
 Entscheiden, ob das Staubecken das gesamte Wasser aufnehmen kann
Nun wird
Entscheiden, ob das Staubecken das gesamte Wasser aufnehmen kann
Nun wird  für
für  mit
mit
betrachtet. Weiterhin weißt du, dass das Staubecken zum Zeitpunkt  noch 20.000\,m
noch 20.000\,m Wasser aufnehmen kann. Deine Aufgabe ist es nun, zu entscheiden, ob das Staubecken das gesamte Wasser aus den beiden Bächen während der 24 Stunden des Beobachtungszeitraums aufnehmen könnte.
Wasser aufnehmen kann. Deine Aufgabe ist es nun, zu entscheiden, ob das Staubecken das gesamte Wasser aus den beiden Bächen während der 24 Stunden des Beobachtungszeitraums aufnehmen könnte.
Da Funktion die Gesamtzuflussrate beschreibt, repräsentiert das Integral über diese Funktion, das Volumen des Wassers, welches nach
die Gesamtzuflussrate beschreibt, repräsentiert das Integral über diese Funktion, das Volumen des Wassers, welches nach  in das Staubecken fließt. Willst du hier bestimmen, welches Volumen das Wasser besitzt, welches nach
in das Staubecken fließt. Willst du hier bestimmen, welches Volumen das Wasser besitzt, welches nach  in das Staubecken fließt, so musst du hier über
in das Staubecken fließt, so musst du hier über  über den gesamten Beobachtungszeitraum (
über den gesamten Beobachtungszeitraum (![\(t \in \left[0;24\right]\)](https://mathjax.schullv.de/ae8655d10c72de999b0574df7147ab659e2429f487aef39b9e199fa49df0159e?color=5a5a5a) ) integrieren.
) integrieren.
Dabei gibt es zwei Lösungswege. Die Lösung von Hand und die Lösung mit deinem GTR. Beachte beim Lösen von Hand, dass zum Zeitpunkt noch kein Wasser in das Staubecken geflossen ist und die berechnete Stammfunktion dementsprechend anpassen musst.
noch kein Wasser in das Staubecken geflossen ist und die berechnete Stammfunktion dementsprechend anpassen musst.
 Lösungsweg A: Lösen von Hand
Bestimme das unbestimmte Integral über
Lösungsweg A: Lösen von Hand
Bestimme das unbestimmte Integral über  , um eine Stammfunktion
, um eine Stammfunktion  zu ermitteln:
zu ermitteln:
 Bestimme nun die Integrationskonstante
Bestimme nun die Integrationskonstante  so, dass zum Zeitpunkt
so, dass zum Zeitpunkt  noch kein Wasser ins Staubecken geflossen ist. Setze also
noch kein Wasser ins Staubecken geflossen ist. Setze also  :
:
 Die hier zu betrachtende Stammfunktion von
Die hier zu betrachtende Stammfunktion von  ist also:
ist also:
 .
Integriere nun über den Beobachtungszeitraum, um entscheiden zu können, ob das Staubecken das Wasser aufnehmen kann. Setze dazu die Grenzen der Integration auf
.
Integriere nun über den Beobachtungszeitraum, um entscheiden zu können, ob das Staubecken das Wasser aufnehmen kann. Setze dazu die Grenzen der Integration auf  und
und  :
:
![\(\begin{array}{r@{ = }l@{\hspace{1cm}}l}
I=&\displaystyle\int_{t_1}^{t_2} \left(h_4(t)\right)\mathrm dt = \left[H_4(t)\right]_0^{24} = H_4(24) - H_4(0)\\
=&\frac{1}{8} \cdot 24^4 - \frac{28}{3} \cdot 24^3 + 192 \cdot 24^2 + 740 \cdot 24 - \left(\frac{1}{8} \cdot 0^4 - \frac{28}{3} \cdot 0^3 + 192 \cdot 0^2 + 740 \cdot 0\right)\\
=&41.472 - 129.024 + 110.592 + 17.760\\
=&40.800\\
\end{array}\)](https://mathjax.schullv.de/ba30eb74417bbcdc0dd0ee5392bfcd8ec50248eba861338974f3cf00ee3ac301?color=5a5a5a) Innerhalb des Beobachtungszeitraums fließen 40.800 m
Innerhalb des Beobachtungszeitraums fließen 40.800 m Wasser in das Staubecken. Das Staubecken kann als das nach fließende Wasser nicht aufnehmen.
Wasser in das Staubecken. Das Staubecken kann als das nach fließende Wasser nicht aufnehmen.
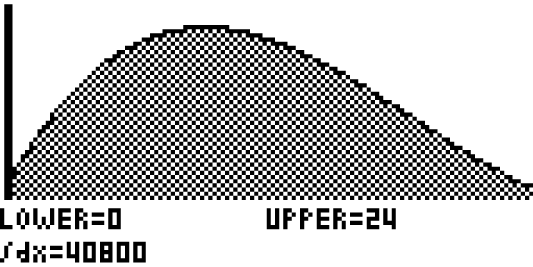
 Lösungsweg B: Lösen mit dem GTR
Wechsle mit deinem GTR in den Y=-Editor und speichere dort den Funktionsterm von
Lösungsweg B: Lösen mit dem GTR
Wechsle mit deinem GTR in den Y=-Editor und speichere dort den Funktionsterm von  . Hast du diesen dort gespeichert, dann lass dir den zugehörigen Graph über GRAPH anzeigen.
. Hast du diesen dort gespeichert, dann lass dir den zugehörigen Graph über GRAPH anzeigen.
Bestimme dann über
das Integral über  in den Grenzen des Beobachtungsintervalls.
in den Grenzen des Beobachtungsintervalls.
![Grafik einer mathematischen Funktion mit Integralberechnung im Intervall [0, 24] auf einem Taschenrechner-Display.](https://www.schullv.de/resources/images/mathe/desktop/interval_ti.png) Innerhalb des Beobachtungszeitraums fließen 40.800 m
Innerhalb des Beobachtungszeitraums fließen 40.800 m Wasser in das Staubecken. Das Staubecken kann als das nach fließende Wasser nicht aufnehmen.
Wasser in das Staubecken. Das Staubecken kann als das nach fließende Wasser nicht aufnehmen.
|
|
Da Funktion
Dabei gibt es zwei Lösungswege. Die Lösung von Hand und die Lösung mit deinem GTR. Beachte beim Lösen von Hand, dass zum Zeitpunkt
Bestimme dann über
|
2nd |
![Grafik einer mathematischen Funktion mit Integralberechnung im Intervall [0, 24] auf einem Taschenrechner-Display.](https://www.schullv.de/resources/images/mathe/desktop/interval_ti.png)
(2)
 Angeben der Bedeutung der Lösung im Sachzusammenhang
In dieser Teilaufgabe hast du die die Gleichung
Angeben der Bedeutung der Lösung im Sachzusammenhang
In dieser Teilaufgabe hast du die die Gleichung
mit der positiven Lösung  gegeben. Deine Aufgabe ist es dabei, die Bedeutung dieser Lösung im Sachzusammenhang anzugeben.
gegeben. Deine Aufgabe ist es dabei, die Bedeutung dieser Lösung im Sachzusammenhang anzugeben.
Mach dir dazu zunächst klar, was die Gleichung ausdrückt: erreicht. Das heißt, ab dem Zeitpunkt
erreicht. Das heißt, ab dem Zeitpunkt  ist das Staubecken am überlaufen.
ist das Staubecken am überlaufen.
|
|
Mach dir dazu zunächst klar, was die Gleichung ausdrückt:
- Es wird wieder über die Funktion
integriert.
- Die untere Grenze entspricht dem Anfang des Beobachtungszeitraums.
- Als obere Grenze des Integrals ergibt sich
.
- Die rechte Seite der Gleichung repräsentiert das Volumen, dass das Staubecken noch aufnehmen kann.
(3)
 Untersuchen, ob das Staubecken im Beobachtungszeitraum überläuft
Der Aufgabenstellung kannst du entnehmen, dass zum Zeitpunkt
Untersuchen, ob das Staubecken im Beobachtungszeitraum überläuft
Der Aufgabenstellung kannst du entnehmen, dass zum Zeitpunkt  ein vorher verschlossener Notablauf geöffnet wird. Durch diesen Notablauf fließt Wasser mit einer konstanten Abflussrate von 2.000
ein vorher verschlossener Notablauf geöffnet wird. Durch diesen Notablauf fließt Wasser mit einer konstanten Abflussrate von 2.000  aus dem Becken ab. Der Notablauf bleibt dabei bis zum Ende des Beobachtungszeitraums geöffnet.
aus dem Becken ab. Der Notablauf bleibt dabei bis zum Ende des Beobachtungszeitraums geöffnet.
Ohne Nachweis darf dabei verwendet werden, dass die Gesamtzuflussrate für größer und für
größer und für  kleiner als 2.000
kleiner als 2.000  ist.
ist.
Du sollst nun untersuchen, ob das Staubecken innerhalb des Beobachtungszeitraums überläuft.
Willst du untersuchen, ob das Staubecken überläuft, so benötigst du zunächst eine Funktion, welche dir das Volumen des Wassers im Staubecken nach dem Zeitpunkt angibt. Verwende dazu wie oben unter anderem die Stammfunktion
angibt. Verwende dazu wie oben unter anderem die Stammfunktion  .
.
Von oben und dem gegebenen Schaubild weißt du, dass die Funktion im Intervall
im Intervall
 oberhalb von 2.000
oberhalb von 2.000  und im Intervall
und im Intervall  unterhalb von 2.000
unterhalb von 2.000  . Subtrahierst du nun in diesem Bereich die 2.000
. Subtrahierst du nun in diesem Bereich die 2.000  pro Stunde, so besitzt die veränderte Funktion
pro Stunde, so besitzt die veränderte Funktion  in diesem Bereich eine Nullstelle, mit einem Vorzeichenwechsel von
in diesem Bereich eine Nullstelle, mit einem Vorzeichenwechsel von  zu
zu  . Die zu
. Die zu  zugehörige Stammfunktion besitzt also in diesem Intervall ein Maximum.
zugehörige Stammfunktion besitzt also in diesem Intervall ein Maximum.
Die für zu betrachtende Funktion
zu betrachtende Funktion  ergibt sich nach der Subtraktion von 2.000
ergibt sich nach der Subtraktion von 2.000  zu:
zu:
Bestimme mit dieser Funktion die Maximalstelle von  . Liegt das Wasservolumen an der bestimmten Maximalstelle dann unter 20.000 m
. Liegt das Wasservolumen an der bestimmten Maximalstelle dann unter 20.000 m , dann läuft das Staubecken nicht über.
, dann läuft das Staubecken nicht über.
Gehe beim Lösen dieser Aufgabe also so vor: der ersten Ableitung von
der ersten Ableitung von  bestimmst du zunächst die Nullstellen dieser Funktion. Nutze dazu deinen GTR und übertrage zunächst den Funktionsterm von
bestimmst du zunächst die Nullstellen dieser Funktion. Nutze dazu deinen GTR und übertrage zunächst den Funktionsterm von  in den Y=-Editor deines GTR. Lasse dir anschließend mit GRAPH den Graphen der Funktion
in den Y=-Editor deines GTR. Lasse dir anschließend mit GRAPH den Graphen der Funktion  anzeigen und bestimme über
anzeigen und bestimme über
die Nullstellen.
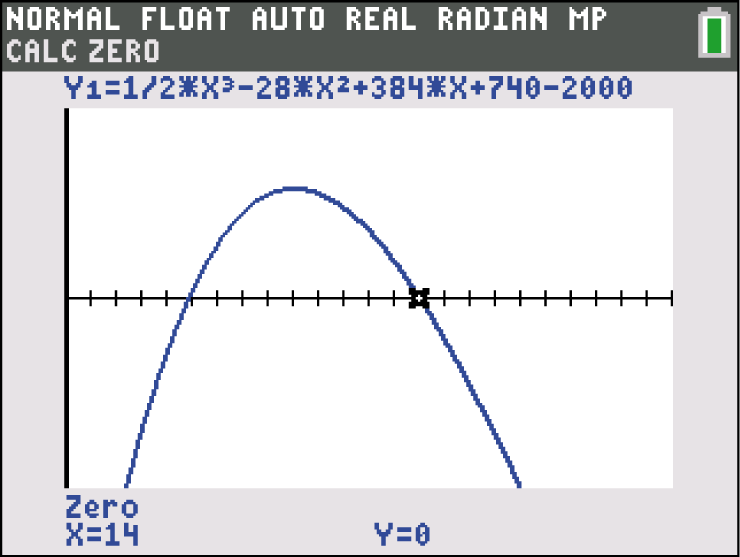 Die Nullstellen von
Die Nullstellen von  liegen also bei
liegen also bei  und
und  . Da
. Da  außerhalb des betrachteten Bereichs liegt und bei
außerhalb des betrachteten Bereichs liegt und bei  offensichtlich ein Vorzeichenwechsel von
offensichtlich ein Vorzeichenwechsel von  zu
zu  vorliegt, handelt es sich bei
vorliegt, handelt es sich bei  um die hier gesuchte Maximalstelle.
2. Schritt: Berechnen des Wasservolumen an der Maximalstelle
Das Wasservolumen an der Maximalstelle
um die hier gesuchte Maximalstelle.
2. Schritt: Berechnen des Wasservolumen an der Maximalstelle
Das Wasservolumen an der Maximalstelle  berechnest du nun, indem du diesen Wert in den Funktionsterm einer Stammfunktion von
berechnest du nun, indem du diesen Wert in den Funktionsterm einer Stammfunktion von  einsetzt. Die Stammfunktion
einsetzt. Die Stammfunktion  von
von  hast du bereits im vorhergegangenen Aufgabenteil berechnet. Subtrahiere von dieser Funktion die Abflussrate um eine Stammfunktion von
hast du bereits im vorhergegangenen Aufgabenteil berechnet. Subtrahiere von dieser Funktion die Abflussrate um eine Stammfunktion von  bestimmt zu haben. Beachte dabei, dass erst ab dem Zeitpunkt
bestimmt zu haben. Beachte dabei, dass erst ab dem Zeitpunkt  die Abflussrate von
die Abflussrate von  m
m pro Stunde vorliegt.
pro Stunde vorliegt.
 Setze nun
Setze nun  ein, um das Wasservolumen zum Zeitpunkt des Maximums zu bestimmen:
ein, um das Wasservolumen zum Zeitpunkt des Maximums zu bestimmen:
 Es befinden sich also maximal 19.183,3 m
Es befinden sich also maximal 19.183,3 m Wasser im Staubecken. Da dieser Wert unter der Grenze von 20.000 m
Wasser im Staubecken. Da dieser Wert unter der Grenze von 20.000 m liegt, ist das Staubecken nicht am überlaufen.
liegt, ist das Staubecken nicht am überlaufen.
Ohne Nachweis darf dabei verwendet werden, dass die Gesamtzuflussrate für
Du sollst nun untersuchen, ob das Staubecken innerhalb des Beobachtungszeitraums überläuft.
Willst du untersuchen, ob das Staubecken überläuft, so benötigst du zunächst eine Funktion, welche dir das Volumen des Wassers im Staubecken nach dem Zeitpunkt
Von oben und dem gegebenen Schaubild weißt du, dass die Funktion
Die für
|
|
Gehe beim Lösen dieser Aufgabe also so vor:
- Bestimme die Maximalstelle von
über die notwendige und hinreichende Bedingung für Maxima.
- Berechne das Wasservolumen an der Maximalstelle.
- Vergleiche berechneten mit gegebenen Wert.
|
2nd |

a) (1)
 Berechnen der Gesamtzuflussrate zu Beginn und am Ende der Beobachtung
Der Aufgabenstellung kannst du entnehmen, dass in ein Staubecken zwei Bäche hineinfließen. Nach Regenfällen unterschiedlicher Dauer und Stärke können die momentanen Zuflussraten aus den beiden Bächen durch die Funktion
Berechnen der Gesamtzuflussrate zu Beginn und am Ende der Beobachtung
Der Aufgabenstellung kannst du entnehmen, dass in ein Staubecken zwei Bäche hineinfließen. Nach Regenfällen unterschiedlicher Dauer und Stärke können die momentanen Zuflussraten aus den beiden Bächen durch die Funktion  für Bach 1 und
für Bach 1 und  für Bach 2 für einen bestimmten Beobachtungszeitraum modelliert werden. Die Gesamtzuflussrate aus den beiden Bächen wird durch die Funktion
für Bach 2 für einen bestimmten Beobachtungszeitraum modelliert werden. Die Gesamtzuflussrate aus den beiden Bächen wird durch die Funktion  beschrieben.
beschrieben.
Die Funktionen und
und  sind für
sind für  und
und  wie folgt angegeben:
wie folgt angegeben:
 ist dabei in Stunden (h) angegeben. Die Funktionswerte
ist dabei in Stunden (h) angegeben. Die Funktionswerte  ,
,  und
und  beschreiben die Zuflussrate in
beschreiben die Zuflussrate in  . Der Beobachtungszeitraum beginnt beim Zeitpunkt
. Der Beobachtungszeitraum beginnt beim Zeitpunkt  und endet zum Zeitpunkt
und endet zum Zeitpunkt  .
.
Deine Aufgabe ist es nun, die Gesamtzuflussrate zu Beginn und am Ende des Beobachtungszeitraums zu bestimmen. Zu betrachten ist hier also Funktion , da diese die Gesamtzuflussrate in das Staubecken beschreibt. Von oben weißt du, dass die Beobachtung zum Zeitpunkt
, da diese die Gesamtzuflussrate in das Staubecken beschreibt. Von oben weißt du, dass die Beobachtung zum Zeitpunkt  startet und am Zeitpunkt
startet und am Zeitpunkt  endet.
endet.
Willst du diese Aufgabe lösen, so berechnest du die Funktionswerte von an diesen Zeitpunkten.
Gesamtzuflussrate am Beobachtungsbeginn
an diesen Zeitpunkten.
Gesamtzuflussrate am Beobachtungsbeginn  :
:
 .
Gesamtzuflussrate am Beobachtungsende
.
Gesamtzuflussrate am Beobachtungsende  :
:
 Die Gesamtzuflussrate ist zu Beginn und am Ende des Beobachtungszeitraums
Die Gesamtzuflussrate ist zu Beginn und am Ende des Beobachtungszeitraums  .
.
Die Funktionen
Deine Aufgabe ist es nun, die Gesamtzuflussrate zu Beginn und am Ende des Beobachtungszeitraums zu bestimmen. Zu betrachten ist hier also Funktion
Willst du diese Aufgabe lösen, so berechnest du die Funktionswerte von
(2)
 Zeigen, dass
Zeigen, dass  durch den Funktionsterm
durch den Funktionsterm  dargestellt werden kann
Nun sollst du zeigen, dass der Funktionsterm der Funktion
dargestellt werden kann
Nun sollst du zeigen, dass der Funktionsterm der Funktion  , die die Zuflussrate von Bach 2 in das Staubecken repräsentiert, durch den folgenden Funktionsterm beschrieben werden kann:
, die die Zuflussrate von Bach 2 in das Staubecken repräsentiert, durch den folgenden Funktionsterm beschrieben werden kann:
Willst du diesen Sachverhalt zeigen, so musst du hier Funktion  betrachten. Diese beschreibt die Gesamtzuflussrate in das Staubecken. Da außer Bach 1, beschrieben durch
betrachten. Diese beschreibt die Gesamtzuflussrate in das Staubecken. Da außer Bach 1, beschrieben durch  und Bach 2, beschrieben durch
und Bach 2, beschrieben durch  , kein weiterer Fluss in das Staubecken fließt, ergibt sich die Gesamtzuflussrate aus der Summe der Zuflussraten von Bach 1 und Bach 2.
Für den Funktionsterm von
, kein weiterer Fluss in das Staubecken fließt, ergibt sich die Gesamtzuflussrate aus der Summe der Zuflussraten von Bach 1 und Bach 2.
Für den Funktionsterm von  gilt also:
gilt also:
 Stelle nach
Stelle nach  um und setze ein, um den Sachverhalt hier zu zeigen:
um und setze ein, um den Sachverhalt hier zu zeigen:
 Da der berechnete und der gegebene Funktionsterm übereinstimmen, hast du die Aufgabe hier richtig gelöst.
Da der berechnete und der gegebene Funktionsterm übereinstimmen, hast du die Aufgabe hier richtig gelöst.
|
|
(3)
 Begründen, dass Zuflussrate aus Bach 2 größer ist als die von Bach 1
Nun ist es deine Aufgabe, zu begründen, dass unabhängig von Parameter
Begründen, dass Zuflussrate aus Bach 2 größer ist als die von Bach 1
Nun ist es deine Aufgabe, zu begründen, dass unabhängig von Parameter  , die Zuflussrate aus Bach 2 für alle
, die Zuflussrate aus Bach 2 für alle ![\(t \in \left[0;6a\right]\)](https://mathjax.schullv.de/db6125b4f8e52a1658217cff72567d2917947e05036bef65c36029c955127c99?color=5a5a5a) größer ist als die Zuflussrate aus Bach 1. Willst du zeigen, dass die Zuflussrate von Bach 2 im gesamten Beobachtungszeitraum größer als die Zuflussrate von Bach 1 ist, so musst du zeigen, dass der Graph von
größer ist als die Zuflussrate aus Bach 1. Willst du zeigen, dass die Zuflussrate von Bach 2 im gesamten Beobachtungszeitraum größer als die Zuflussrate von Bach 1 ist, so musst du zeigen, dass der Graph von  innerhalb des Beobachtungszeitraums oberhalb des Graphen von
innerhalb des Beobachtungszeitraums oberhalb des Graphen von  verläuft.
verläuft.
Willst du dies begründen, so betrachtest du hier die Differenz zwischen dem Graphen von und
und  . Diese Differenz kann durch die Differenzfunktion
. Diese Differenz kann durch die Differenzfunktion  beschrieben werden, welche sich wie folgt berechnen lässt:
beschrieben werden, welche sich wie folgt berechnen lässt:
Willst du zeigen, dass die Zuflussrate aus Bach 2 immer größer ist als die Zuflussrate aus Bach 1, so zeigst du hier, dass die Differenz zwischen diesen Funktionen unabhängig von  immer größer gleich Null ist. Bezogen auf
immer größer gleich Null ist. Bezogen auf  und den Beobachtungszeitraum gilt also:
und den Beobachtungszeitraum gilt also:
Bilde also zunächst die Funktion  und zeige das Folgendes für diese gilt:
und zeige das Folgendes für diese gilt:
 Berechne die oben angegebene Differenz, um
Berechne die oben angegebene Differenz, um  zu erhalten:
zu erhalten:
 2. Schritt: Untersuchen der Randstellen des Intervalls
Zeige nun, durch Berechnen der Funktionswerte von
2. Schritt: Untersuchen der Randstellen des Intervalls
Zeige nun, durch Berechnen der Funktionswerte von  an den Randstellen
an den Randstellen  und
und  des Intervalls, dass
des Intervalls, dass  unabhängig von
unabhängig von  an diesen Stellen einen Wert größer Null annimmt:
an diesen Stellen einen Wert größer Null annimmt:

 So hast du also gezeigt, dass Funktion
So hast du also gezeigt, dass Funktion  an den Randstellen
an den Randstellen  und
und  des Intervalls unabhängig von
des Intervalls unabhängig von  , oberhalb der Funktion
, oberhalb der Funktion  verläuft.
3. Schritt: Untersuchen des Verhaltens des Graphen von
verläuft.
3. Schritt: Untersuchen des Verhaltens des Graphen von  im Intervall
Untersuche nun das Verhalten des Graphen von
im Intervall
Untersuche nun das Verhalten des Graphen von  innerhalb der Intervallsgrenzen. Um zu zeigen, dass
innerhalb der Intervallsgrenzen. Um zu zeigen, dass  im gesamten Intervall oberhalb von
im gesamten Intervall oberhalb von  verläuft, musst du hier zeigen, dass
verläuft, musst du hier zeigen, dass  innerhalb des Intervalls nur Werte größer Null annimmt.
innerhalb des Intervalls nur Werte größer Null annimmt.
Betrachte dazu den Funktionsterm von :
:
 Da
Da  gilt, handelt es sich hier um eine nach unten geöffnete Parabel. Da diese an den Randstellen
gilt, handelt es sich hier um eine nach unten geöffnete Parabel. Da diese an den Randstellen  und
und  unabhängig von
unabhängig von  Werte größer Null annimmt, muss diese im Intervall
Werte größer Null annimmt, muss diese im Intervall ![\(\left[0;6 \cdot a\right]\)](https://mathjax.schullv.de/e02627b3d24cbaf4002540ab999a6efcd4f13a153ed93465efc9c596c81ef1af?color=5a5a5a) oberhalb der
oberhalb der  -Achse verlaufen. Da die Differenz zwischen
-Achse verlaufen. Da die Differenz zwischen  und
und  im betrachteten Intervall unabhängig von
im betrachteten Intervall unabhängig von  größer Null ist, hast du gezeigt, dass die Zuflussrate von Bach 2 im gesamt betrachteten Zeitraum größer als die Zuflussrate von Bach 1 ist.
größer Null ist, hast du gezeigt, dass die Zuflussrate von Bach 2 im gesamt betrachteten Zeitraum größer als die Zuflussrate von Bach 1 ist.
Willst du dies begründen, so betrachtest du hier die Differenz zwischen dem Graphen von
|
|
|
|
- Zeige, dass
an den Randstellen des betrachteten Intervalls Werte größer Null annimmt.
- Zeige, der Graph von
zwischen den Randstellen oberhalb der
-Achse verläuft.
Betrachte dazu den Funktionsterm von
(4)
 Bestimmen des Zeitpunkts, an dem die Gesamtzuflussrate maximal ist
Zuletzt sollst du hier jenen Zeitpunkt im Beobachtungszeitraum bestimmen, bei dem die Gesamtzuflussrate ihr Maximum annimmt. Du untersuchst also
Bestimmen des Zeitpunkts, an dem die Gesamtzuflussrate maximal ist
Zuletzt sollst du hier jenen Zeitpunkt im Beobachtungszeitraum bestimmen, bei dem die Gesamtzuflussrate ihr Maximum annimmt. Du untersuchst also  auf Maximalstellen.
auf Maximalstellen.
Du weißt, an einer bestimmten Stelle liegt genau dann ein Maximum vor, wenn folgende Bedingungen an dieser erfüllt sind:
liegt genau dann ein Maximum vor, wenn folgende Bedingungen an dieser erfüllt sind:
 und ermittle über Auswerten der oben gegebenen Bedingungen die gesuchte Maximalstelle im Intervall.
und ermittle über Auswerten der oben gegebenen Bedingungen die gesuchte Maximalstelle im Intervall.
Da hier aber ein abgeschlossenes Intervall angegeben ist, musst du hier die Randstellen von und
und  untersuchen, um das globale Maximum im gegebenen Intervall zu ermitteln. Vergleiche dazu die Funktionswerte von
untersuchen, um das globale Maximum im gegebenen Intervall zu ermitteln. Vergleiche dazu die Funktionswerte von  an den Randstellen und beim ermittelten Maximum.
an den Randstellen und beim ermittelten Maximum.
Gehe beim Lösen der Aufgabe also so vor: und
und  ergibt sich hier:
ergibt sich hier:

 2. Schritt: Maximalstellen von
2. Schritt: Maximalstellen von  bestimmen
Bestimme zunächst die Nullstellen von
bestimmen
Bestimme zunächst die Nullstellen von  , um die potentiellen Extremstellen von
, um die potentiellen Extremstellen von  in Abhängigkeit von
in Abhängigkeit von  zu bestimmen:
zu bestimmen:
 Hier liegt eine quadratische Gleichung löse diese mit Hilfe der
Hier liegt eine quadratische Gleichung löse diese mit Hilfe der  -
- - oder der Mitternachtsformel.
- oder der Mitternachtsformel.
 -
- -Formel:
-Formel:
 Mitternachtsformel:
Mitternachtsformel:
 Als potentielle Extremstellen ergeben sich also
Als potentielle Extremstellen ergeben sich also  und
und  . Da für
. Da für 

gilt und diese Extremstelle damit nicht mehr im betrachteten Intervall liegt, wird hier im Folgenden nur noch betrachtet.
Überprüfe nun die hinreichende Bedingung bei
betrachtet.
Überprüfe nun die hinreichende Bedingung bei  , um festzustellen, ob an dieser Stelle eine Maximalstelle vorliegt. Beachte dabei, dass auch hier
, um festzustellen, ob an dieser Stelle eine Maximalstelle vorliegt. Beachte dabei, dass auch hier  gilt.
gilt.
 Bei
Bei  liegt also eine Maximalstelle der Funktion
liegt also eine Maximalstelle der Funktion  vor.
3. Schritt: Überprüfen der Randstellen des Intervalls
Im ersten Aufgabenteil dieser Teilaufgabe hast du bestimmt, dass für die Funktionswerte von
vor.
3. Schritt: Überprüfen der Randstellen des Intervalls
Im ersten Aufgabenteil dieser Teilaufgabe hast du bestimmt, dass für die Funktionswerte von  an den Randstellen, unabhängig von
an den Randstellen, unabhängig von  , folgendes gilt:
, folgendes gilt:
 .
Überprüfe nun den Funktionswert bei
.
Überprüfe nun den Funktionswert bei  , um zu überprüfen, ob an dieser Stelle auch ein globales Maximum vorliegt:
, um zu überprüfen, ob an dieser Stelle auch ein globales Maximum vorliegt:
 Da
Da  gilt, gilt
gilt, gilt  und
und  weshalb bei
weshalb bei  ein globales Maximum vorliegt.
ein globales Maximum vorliegt.
Die hier gesuchte Maximalstelle liegt also bei . Weiterhin wurde gezeigt, dass dieses Maximum ein globales ist.
. Weiterhin wurde gezeigt, dass dieses Maximum ein globales ist.
Du weißt, an einer bestimmten Stelle
- Notwendige Bedingung:
- Hinreichende Bedingung:
Da hier aber ein abgeschlossenes Intervall angegeben ist, musst du hier die Randstellen von
Gehe beim Lösen der Aufgabe also so vor:
- Bestimme die benötigten Ableitungsfunktionen
und
.
- Bestimme über die notwendige und hinreichende Bedingung die Maximalstellen von
.
- Untersuche die Funktionswerte an den Rand- und Maximalstellen.
gilt und diese Extremstelle damit nicht mehr im betrachteten Intervall liegt, wird hier im Folgenden nur noch
Die hier gesuchte Maximalstelle liegt also bei
b) (1)
 Bestimmen der Wendestelle von
Bestimmen der Wendestelle von  Hier ist es deine Aufgabe die Wendestelle der Funktion
Hier ist es deine Aufgabe die Wendestelle der Funktion  zu bestimmen. Da eine Wendestelle einem Extremum der ersten Ableitung der betrachteten Funktion entspricht, müssen hier die ersten drei Ableitungen von
zu bestimmen. Da eine Wendestelle einem Extremum der ersten Ableitung der betrachteten Funktion entspricht, müssen hier die ersten drei Ableitungen von  betrachtet werden.
betrachtet werden.
Beachte dabei, dass du die ersten beiden Ableitungen und
und  bereits im vorhergegangenen Aufgabenteil bestimmt hast. Liegt dann an einer bestimmten Stelle
bereits im vorhergegangenen Aufgabenteil bestimmt hast. Liegt dann an einer bestimmten Stelle  von
von  eine Wendestelle vor, so sind an dieser Stelle folgende Bedingungen erfüllt:
eine Wendestelle vor, so sind an dieser Stelle folgende Bedingungen erfüllt:
 zu bestimmen.
1. Schritt: Bestimmen der dritten Ableitungsfunktion von
zu bestimmen.
1. Schritt: Bestimmen der dritten Ableitungsfunktion von  1cm
Mit Hilfe der zweiten Ableitungsfunktion von
1cm
Mit Hilfe der zweiten Ableitungsfunktion von  , welche du im vorherigen Aufgabenteil bestimmt hast, ergibt sich
, welche du im vorherigen Aufgabenteil bestimmt hast, ergibt sich  zu:
zu:
 2. Schritt: Bestimmen der Wendestelle von
2. Schritt: Bestimmen der Wendestelle von  Bestimme nun die Wendestelle von
Bestimme nun die Wendestelle von  , indem du zunächst die Nullstellen (notwendige Bedingung) von
, indem du zunächst die Nullstellen (notwendige Bedingung) von  bestimmst:
bestimmst:
 Da für
Da für  :
:

für alle gilt, liegt eine Wendestelle der Funktion
gilt, liegt eine Wendestelle der Funktion  bei
bei  vor.
vor.
Beachte dabei, dass du die ersten beiden Ableitungen
- Notwendige Bedingung:
- Hinreichende Bedingung:
für alle
(2) + (3)
 Zeitpunkt an dem sich die Gesamtzuflussrate am stärksten ändert
Nun sollst du jenen Zeitpunkt im Beobachtungszeitraums bestimmen, zu dem sich die Gesamtzuflussrate am stärksten ändert. Der Zeitpunkt, an dem sich die Gesamtzuflussrate am stärksten ändert ist ein Punkt mit extremaler Steigung.
Rein intuitiv würde man sagen, dieser Punkt ist schon gefunden und entspricht dem Wendepunkt der Funktion
Zeitpunkt an dem sich die Gesamtzuflussrate am stärksten ändert
Nun sollst du jenen Zeitpunkt im Beobachtungszeitraums bestimmen, zu dem sich die Gesamtzuflussrate am stärksten ändert. Der Zeitpunkt, an dem sich die Gesamtzuflussrate am stärksten ändert ist ein Punkt mit extremaler Steigung.
Rein intuitiv würde man sagen, dieser Punkt ist schon gefunden und entspricht dem Wendepunkt der Funktion  . Da
. Da  hier jedoch auf einem abgeschlossenen Intervall untersucht wird, müssen hier, wie auch schon zu vor, die Randstellen des Intervalls untersucht werden.
hier jedoch auf einem abgeschlossenen Intervall untersucht wird, müssen hier, wie auch schon zu vor, die Randstellen des Intervalls untersucht werden.
Willst du also die den Zeitpunkt bestimmen, an dem sich die Gesamtzuflussrate im Zeitraum am stärksten ändert, so gehe hier so vor: ,
,  und
und  in
in  ein, um die Steigung der Gesamtzuflussraten an diesen Zeitpunkten zu bestimmen:
ein, um die Steigung der Gesamtzuflussraten an diesen Zeitpunkten zu bestimmen:
 2. Schritt: Bestimmen der Stelle mit betragsmäßig größter Steigung
Um nun die Stelle mit der betragsmäßig größten Steigung zu berechnen, musst du dir die oben berechneten Steigungen noch einmal etwas genauer ansehen. Du siehst, dass die Steigung an der Wendestelle
2. Schritt: Bestimmen der Stelle mit betragsmäßig größter Steigung
Um nun die Stelle mit der betragsmäßig größten Steigung zu berechnen, musst du dir die oben berechneten Steigungen noch einmal etwas genauer ansehen. Du siehst, dass die Steigung an der Wendestelle  für jedes
für jedes  betragsmäßig kleiner ist wie die Steigungen bei
betragsmäßig kleiner ist wie die Steigungen bei  . Die Steigung bei
. Die Steigung bei  ist sogar betragsmäßig kleiner als bei
ist sogar betragsmäßig kleiner als bei  und
und  .
.
Es folgt also, dass für der Zeitpunkt an dem sich die Gesamtzuflussrate am stärksten ändert bei
der Zeitpunkt an dem sich die Gesamtzuflussrate am stärksten ändert bei  liegt.
liegt.
 Bedeutung der Wendestelle aus (1) im Zusammenhang angeben
Der Zeitpunkt an dem sich die Gesamtzuflussrate lokal am stärksten ändert ist der Wendepunkt. Das heißt dieser Zeitpunkt liegt bei
Bedeutung der Wendestelle aus (1) im Zusammenhang angeben
Der Zeitpunkt an dem sich die Gesamtzuflussrate lokal am stärksten ändert ist der Wendepunkt. Das heißt dieser Zeitpunkt liegt bei  vor, mit
vor, mit  . Die Wendestelle entspricht also jener Stelle, an dem sich die Gesamtzuflussrate lokal am stärksten innerhalb des Betrachtungszeitraums
. Die Wendestelle entspricht also jener Stelle, an dem sich die Gesamtzuflussrate lokal am stärksten innerhalb des Betrachtungszeitraums  ändert.
ändert.
Willst du also die den Zeitpunkt bestimmen, an dem sich die Gesamtzuflussrate im Zeitraum am stärksten ändert, so gehe hier so vor:
- Bestimme die Steigung im Wendepunkt
- Bestimme die Steigung an den Randstellen
und
- Vergleiche die Steigungen und bestimme das globale Extremum der Steigung. Diese liegt dann in dem Punkt, mit dem betragsmäßig größten Steigung
Es folgt also, dass für
c) (1)
 Entscheiden, ob das Staubecken das gesamte Wasser aufnehmen kann
Nun wird
Entscheiden, ob das Staubecken das gesamte Wasser aufnehmen kann
Nun wird  für
für  mit
mit
betrachtet. Weiterhin weißt du, dass das Staubecken zum Zeitpunkt  noch 20.000\,m
noch 20.000\,m Wasser aufnehmen kann. Deine Aufgabe ist es nun, zu entscheiden, ob das Staubecken das gesamte Wasser aus den beiden Bächen während der 24 Stunden des Beobachtungszeitraums aufnehmen könnte.
Wasser aufnehmen kann. Deine Aufgabe ist es nun, zu entscheiden, ob das Staubecken das gesamte Wasser aus den beiden Bächen während der 24 Stunden des Beobachtungszeitraums aufnehmen könnte.
Da Funktion die Gesamtzuflussrate beschreibt, repräsentiert das Integral über diese Funktion, das Volumen des Wassers, welches nach
die Gesamtzuflussrate beschreibt, repräsentiert das Integral über diese Funktion, das Volumen des Wassers, welches nach  in das Staubecken fließt. Willst du hier bestimmen, welches Volumen das Wasser besitzt, welches nach
in das Staubecken fließt. Willst du hier bestimmen, welches Volumen das Wasser besitzt, welches nach  in das Staubecken fließt, so musst du hier über
in das Staubecken fließt, so musst du hier über  über den gesamten Beobachtungszeitraum (
über den gesamten Beobachtungszeitraum (![\(t \in \left[0;24\right]\)](https://mathjax.schullv.de/ae8655d10c72de999b0574df7147ab659e2429f487aef39b9e199fa49df0159e?color=5a5a5a) ) integrieren.
) integrieren.
Dabei gibt es zwei Lösungswege. Die Lösung von Hand und die Lösung mit deinem GTR. Beachte beim Lösen von Hand, dass zum Zeitpunkt noch kein Wasser in das Staubecken geflossen ist und die berechnete Stammfunktion dementsprechend anpassen musst.
noch kein Wasser in das Staubecken geflossen ist und die berechnete Stammfunktion dementsprechend anpassen musst.
 Lösungsweg A: Lösen von Hand
Bestimme das unbestimmte Integral über
Lösungsweg A: Lösen von Hand
Bestimme das unbestimmte Integral über  , um eine Stammfunktion
, um eine Stammfunktion  zu ermitteln:
zu ermitteln:
 Bestimme nun die Integrationskonstante
Bestimme nun die Integrationskonstante  so, dass zum Zeitpunkt
so, dass zum Zeitpunkt  noch kein Wasser ins Staubecken geflossen ist. Setze also
noch kein Wasser ins Staubecken geflossen ist. Setze also  :
:
 Die hier zu betrachtende Stammfunktion von
Die hier zu betrachtende Stammfunktion von  ist also:
ist also:
 .
Integriere nun über den Beobachtungszeitraum, um entscheiden zu können, ob das Staubecken das Wasser aufnehmen kann. Setze dazu die Grenzen der Integration auf
.
Integriere nun über den Beobachtungszeitraum, um entscheiden zu können, ob das Staubecken das Wasser aufnehmen kann. Setze dazu die Grenzen der Integration auf  und
und  :
:
![\(\begin{array}{r@{ = }l@{\hspace{1cm}}l}
I=&\displaystyle\int_{t_1}^{t_2} \left(h_4(t)\right)\mathrm dt = \left[H_4(t)\right]_0^{24} = H_4(24) - H_4(0)\\
=&\frac{1}{8} \cdot 24^4 - \frac{28}{3} \cdot 24^3 + 192 \cdot 24^2 + 740 \cdot 24 - \left(\frac{1}{8} \cdot 0^4 - \frac{28}{3} \cdot 0^3 + 192 \cdot 0^2 + 740 \cdot 0\right)\\
=&41.472 - 129.024 + 110.592 + 17.760\\
=&40.800\\
\end{array}\)](https://mathjax.schullv.de/ba30eb74417bbcdc0dd0ee5392bfcd8ec50248eba861338974f3cf00ee3ac301?color=5a5a5a) Innerhalb des Beobachtungszeitraums fließen 40.800 m
Innerhalb des Beobachtungszeitraums fließen 40.800 m Wasser in das Staubecken. Das Staubecken kann als das nach fließende Wasser nicht aufnehmen.
Wasser in das Staubecken. Das Staubecken kann als das nach fließende Wasser nicht aufnehmen.
 Lösungsweg B: Lösen mit dem GTR
Wechsle mit deinem GTR in das Graphs-Menü und speichere dort den Funktionsterm von
Lösungsweg B: Lösen mit dem GTR
Wechsle mit deinem GTR in das Graphs-Menü und speichere dort den Funktionsterm von  . Hast du diesen dort gespeichert, dann lass dir den zugehörigen Graph über EXE anzeigen.
. Hast du diesen dort gespeichert, dann lass dir den zugehörigen Graph über EXE anzeigen.
Bestimme dann über
das Integral über  in den Grenzen des Beobachtungsintervalls.
in den Grenzen des Beobachtungsintervalls.
 Innerhalb des Beobachtungszeitraums fließen 40.800 m
Innerhalb des Beobachtungszeitraums fließen 40.800 m Wasser in das Staubecken. Das Staubecken kann als das nach fließende Wasser nicht aufnehmen.
Wasser in das Staubecken. Das Staubecken kann als das nach fließende Wasser nicht aufnehmen.
|
|
Da Funktion
Dabei gibt es zwei Lösungswege. Die Lösung von Hand und die Lösung mit deinem GTR. Beachte beim Lösen von Hand, dass zum Zeitpunkt
Bestimme dann über
|
SHIFT |

(2)
 Angeben der Bedeutung der Lösung im Sachzusammenhang
In dieser Teilaufgabe hast du die die Gleichung
Angeben der Bedeutung der Lösung im Sachzusammenhang
In dieser Teilaufgabe hast du die die Gleichung
mit der positiven Lösung  gegeben. Deine Aufgabe ist es dabei, die Bedeutung dieser Lösung im Sachzusammenhang anzugeben.
gegeben. Deine Aufgabe ist es dabei, die Bedeutung dieser Lösung im Sachzusammenhang anzugeben.
Mach dir dazu zunächst klar, was die Gleichung ausdrückt: erreicht. Das heißt, ab dem Zeitpunkt
erreicht. Das heißt, ab dem Zeitpunkt  ist das Staubecken am überlaufen.
ist das Staubecken am überlaufen.
|
|
Mach dir dazu zunächst klar, was die Gleichung ausdrückt:
- Es wird wieder über die Funktion
integriert.
- Die untere Grenze entspricht dem Anfang des Beobachtungszeitraums.
- Als obere Grenze des Integrals ergibt sich
.
- Die rechte Seite der Gleichung repräsentiert das Volumen, dass das Staubecken noch aufnehmen kann.
(3)
 Untersuchen, ob das Staubecken im Beobachtungszeitraum überläuft
Der Aufgabenstellung kannst du entnehmen, dass zum Zeitpunkt
Untersuchen, ob das Staubecken im Beobachtungszeitraum überläuft
Der Aufgabenstellung kannst du entnehmen, dass zum Zeitpunkt  ein vorher verschlossener Notablauf geöffnet wird. Durch diesen Notablauf fließt Wasser mit einer konstanten Abflussrate von 2.000
ein vorher verschlossener Notablauf geöffnet wird. Durch diesen Notablauf fließt Wasser mit einer konstanten Abflussrate von 2.000  aus dem Becken ab. Der Notablauf bleibt dabei bis zum Ende des Beobachtungszeitraums geöffnet.
aus dem Becken ab. Der Notablauf bleibt dabei bis zum Ende des Beobachtungszeitraums geöffnet.
Ohne Nachweis darf dabei verwendet werden, dass die Gesamtzuflussrate für größer und für
größer und für  kleiner als 2.000
kleiner als 2.000  ist.
ist.
Du sollst nun untersuchen, ob das Staubecken innerhalb des Beobachtungszeitraums überläuft.
Willst du untersuchen, ob das Staubecken überläuft, so benötigst du zunächst eine Funktion, welche dir das Volumen des Wassers im Staubecken nach dem Zeitpunkt angibt. Verwende dazu wie oben unter anderem die Stammfunktion
angibt. Verwende dazu wie oben unter anderem die Stammfunktion  .
.
Von oben und dem gegebenen Schaubild weißt du, dass die Funktion im Intervall
im Intervall
 oberhalb von 2.000
oberhalb von 2.000  und im Intervall
und im Intervall  unterhalb von 2.000
unterhalb von 2.000  . Subtrahierst du nun in diesem Bereich die 2.000
. Subtrahierst du nun in diesem Bereich die 2.000  pro Stunde, so besitzt die veränderte Funktion
pro Stunde, so besitzt die veränderte Funktion  in diesem Bereich eine Nullstelle, mit einem Vorzeichenwechsel von
in diesem Bereich eine Nullstelle, mit einem Vorzeichenwechsel von  zu
zu  . Die zu
. Die zu  zugehörige Stammfunktion besitzt also in diesem Intervall ein Maximum.
zugehörige Stammfunktion besitzt also in diesem Intervall ein Maximum.
Die für zu betrachtende Funktion
zu betrachtende Funktion  ergibt sich nach der Subtraktion von 2.000
ergibt sich nach der Subtraktion von 2.000  zu:
zu:
Bestimme mit dieser Funktion die Maximalstelle von  . Liegt das Wasservolumen an der bestimmten Maximalstelle dann unter 20.000 m
. Liegt das Wasservolumen an der bestimmten Maximalstelle dann unter 20.000 m , dann läuft das Staubecken nicht über.
, dann läuft das Staubecken nicht über.
Gehe beim Lösen dieser Aufgabe also so vor: der ersten Ableitung von
der ersten Ableitung von  bestimmst du zunächst die Nullstellen dieser Funktion. Nutze dazu deinen GTR und übertrage zunächst den Funktionsterm von
bestimmst du zunächst die Nullstellen dieser Funktion. Nutze dazu deinen GTR und übertrage zunächst den Funktionsterm von  in das Graphs-Menü deines GTR. Lasse dir anschließend mit EXE den Graphen der Funktion
in das Graphs-Menü deines GTR. Lasse dir anschließend mit EXE den Graphen der Funktion  anzeigen und bestimme über
anzeigen und bestimme über
die Nullstellen.
 Die Nullstellen von
Die Nullstellen von  liegen also bei
liegen also bei  und
und  . Da
. Da  außerhalb des betrachteten Bereichs liegt und bei
außerhalb des betrachteten Bereichs liegt und bei  offensichtlich ein Vorzeichenwechsel von
offensichtlich ein Vorzeichenwechsel von  zu
zu  vorliegt, handelt es sich bei
vorliegt, handelt es sich bei  um die hier gesuchte Maximalstelle.
2. Schritt: Berechnen des Wasservolumen an der Maximalstelle
Das Wasservolumen an der Maximalstelle
um die hier gesuchte Maximalstelle.
2. Schritt: Berechnen des Wasservolumen an der Maximalstelle
Das Wasservolumen an der Maximalstelle  berechnest du nun, indem du diesen Wert in den Funktionsterm einer Stammfunktion von
berechnest du nun, indem du diesen Wert in den Funktionsterm einer Stammfunktion von  einsetzt. Die Stammfunktion
einsetzt. Die Stammfunktion  von
von  hast du bereits im vorhergegangenen Aufgabenteil berechnet. Subtrahiere von dieser Funktion die Abflussrate um eine Stammfunktion von
hast du bereits im vorhergegangenen Aufgabenteil berechnet. Subtrahiere von dieser Funktion die Abflussrate um eine Stammfunktion von  bestimmt zu haben. Beachte dabei, dass erst ab dem Zeitpunkt
bestimmt zu haben. Beachte dabei, dass erst ab dem Zeitpunkt  die Abflussrate von
die Abflussrate von  m
m pro Stunde vorliegt.
pro Stunde vorliegt.
 Setze nun
Setze nun  ein, um das Wasservolumen zum Zeitpunkt des Maximums zu bestimmen:
ein, um das Wasservolumen zum Zeitpunkt des Maximums zu bestimmen:
 Es befinden sich also maximal 19.183,3 m
Es befinden sich also maximal 19.183,3 m Wasser im Staubecken. Da dieser Wert unter der Grenze von 20.000 m
Wasser im Staubecken. Da dieser Wert unter der Grenze von 20.000 m liegt, ist das Staubecken nicht am überlaufen.
liegt, ist das Staubecken nicht am überlaufen.
Ohne Nachweis darf dabei verwendet werden, dass die Gesamtzuflussrate für
Du sollst nun untersuchen, ob das Staubecken innerhalb des Beobachtungszeitraums überläuft.
Willst du untersuchen, ob das Staubecken überläuft, so benötigst du zunächst eine Funktion, welche dir das Volumen des Wassers im Staubecken nach dem Zeitpunkt
Von oben und dem gegebenen Schaubild weißt du, dass die Funktion
Die für
|
|
Gehe beim Lösen dieser Aufgabe also so vor:
- Bestimme die Maximalstelle von
über die notwendige und hinreichende Bedingung für Maxima.
- Berechne das Wasservolumen an der Maximalstelle.
- Vergleiche berechneten mit gegebenen Wert.
|
SHIFT |
