Wahlplichtteil
Aufgabe 1 – Analysis
Gegeben ist die in
a)
Berechne den Wert von  für den
für den  eine Nullstelle von
eine Nullstelle von  ist.
ist.
b)
Alle Graphen von  haben einen von
haben einen von  abhängigen Extrempunkt. Alle diese Extrempunkte liegen auf dem Graphen der Ortskurve
abhängigen Extrempunkt. Alle diese Extrempunkte liegen auf dem Graphen der Ortskurve  Bestimme eine Gleichung der Ortskurve
Bestimme eine Gleichung der Ortskurve 
(1 + 4 Punkte)
Aufgabe 2 – Analysis
Gegeben ist die in
a)
Zeige, dass  die erste Ableitung von
die erste Ableitung von  ist.
ist.
b)
Untersuche, für welche Werte des Parameters  der Graph von
der Graph von  eine waagerechte Tangente besitzt.
eine waagerechte Tangente besitzt.
(2 + 3 Punkte)
Aufgabe 3 – Vektorielle Geometrie
Gegeben ist die Ebenenschar
a)
Prüfe, ob  zur Ebenenschar
zur Ebenenschar  gehört.
gehört.
b)
Ermittle eine Gleichung für die Geradenschar  die die Schnittgeraden der Ebenen
die die Schnittgeraden der Ebenen  mit der
mit der  -Ebene enthält.
-Ebene enthält.
(2 + 3 Punkte)
Aufgabe 4 – Vektorielle Geometrie
Wird der Punkt
a)
Bestimme eine Gleichung von  in Koordinatenform.
in Koordinatenform.
b)
Auf der Gerade durch  und
und  liegen die Punkte
liegen die Punkte  und
und  symmetrisch bezüglich
symmetrisch bezüglich  ; dabei liegt
; dabei liegt  bezüglich
bezüglich  auf der gleichen Seite wie
auf der gleichen Seite wie  . Der Abstand von
. Der Abstand von  und
und  ist doppelt so groß wie der Abstand von
ist doppelt so groß wie der Abstand von  und
und  . Bestimme die Koordinaten von
. Bestimme die Koordinaten von  .
.
(3 + 2 Punkte)
Aufgabe 5 – Stochastik
In einem Behälter befinden sich Gummibärchen.
a)
Es befinden sich  rote und
rote und  grüne Gummibärchen im Behälter. Paula nimmt zufällig drei Gummibärchen heraus und isst sie auf. Berechne die Wahrscheinlichkeit, dass sie dabei mindestens zwei rote Gummibärchen isst.
grüne Gummibärchen im Behälter. Paula nimmt zufällig drei Gummibärchen heraus und isst sie auf. Berechne die Wahrscheinlichkeit, dass sie dabei mindestens zwei rote Gummibärchen isst.
b)
Es befinden sich  Gummibärchen im Behälter, von denen genau eines orange ist. Max nimmt zufällig zwei Gummibärchen heraus und isst sie auf. Die Wahrscheinlichkeit, dass er dabei das orangefarbene Gummibärchen isst, beträgt
Gummibärchen im Behälter, von denen genau eines orange ist. Max nimmt zufällig zwei Gummibärchen heraus und isst sie auf. Die Wahrscheinlichkeit, dass er dabei das orangefarbene Gummibärchen isst, beträgt  . Ermittle die Anzahl
. Ermittle die Anzahl  der Gummibärchen im Behälter.
der Gummibärchen im Behälter.
(2 + 3 Punkte)
Aufgabe 6 – Stochastik
Gegeben sind die im Folgenden beschriebenen Zufallsgrößen
a)
Begründe, dass die Wahrscheinlichkeit  mit der Wahrscheinlichkeit
mit der Wahrscheinlichkeit  übereinstimmt.
übereinstimmt.
b)
Die Wahrscheinlichkeitsverteilungen von  und
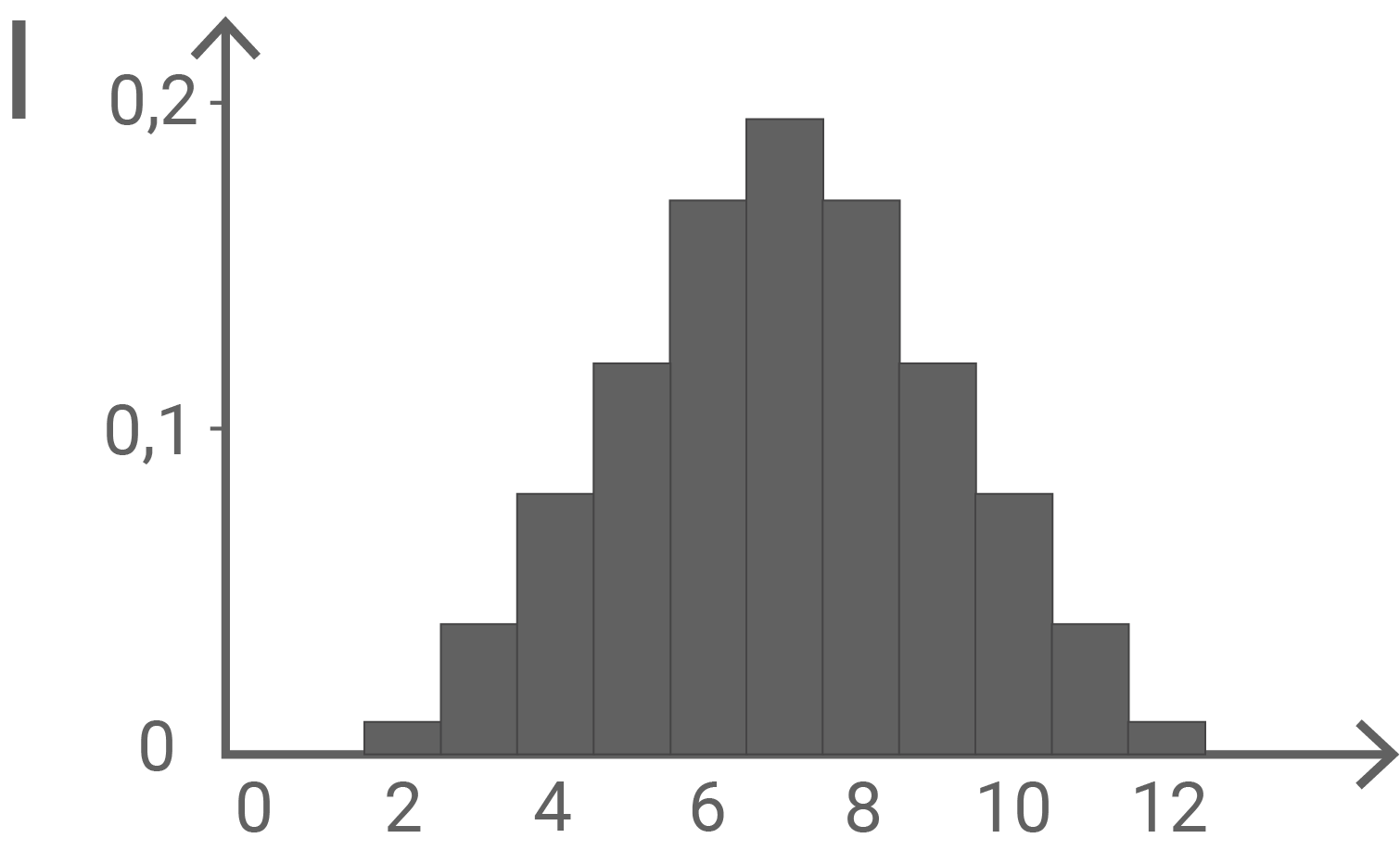
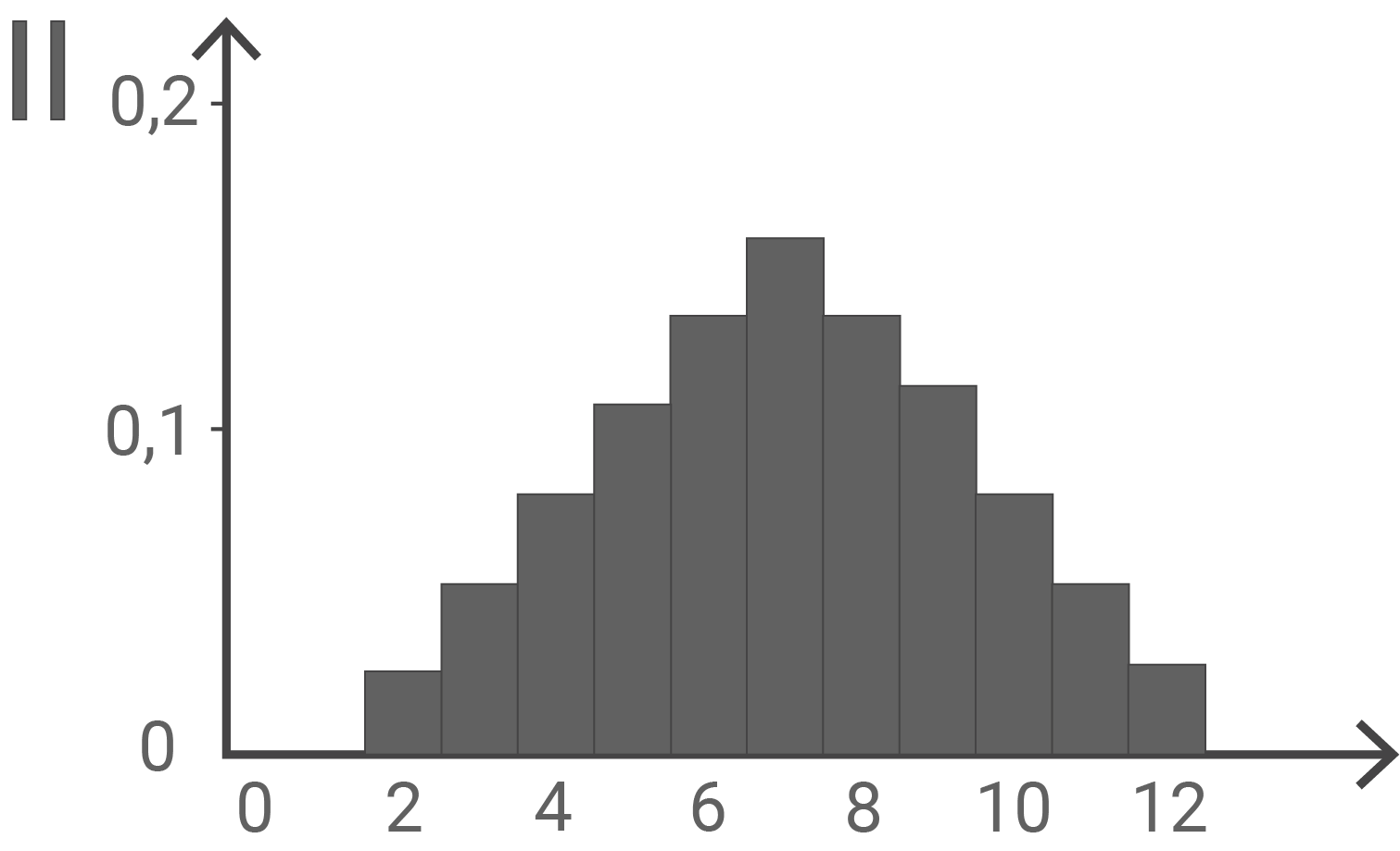
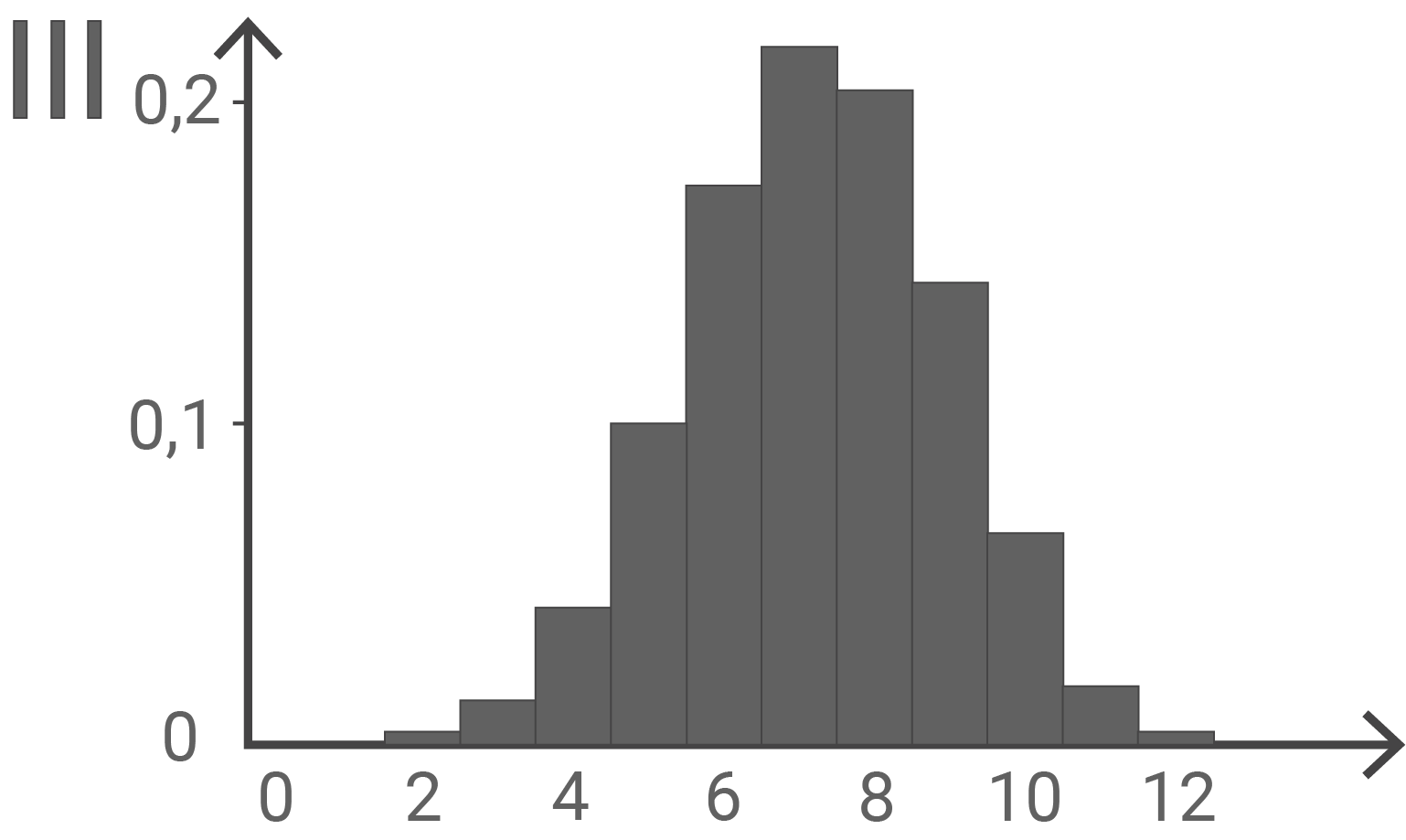
und  werden jeweils durch eines der folgenden Diagramme I, II und III dargestellt. Ordne
werden jeweils durch eines der folgenden Diagramme I, II und III dargestellt. Ordne  und
und  jeweils dem passenden Diagramm zu und begründe deine Zuordnung.
jeweils dem passenden Diagramm zu und begründe deine Zuordnung.
(2 + 3 Punkte)
(10 Punkte)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung 1 – Analysis
a)
b)
1. Schritt: Extremstelle bestimmen
Es gilt:  Notwendige Bedingung für Extremstellen anwenden
Notwendige Bedingung für Extremstellen anwenden
![\(\begin{array}[t]{rll}
f_a](https://mathjax.schullv.de/44324cea77d5e06dfc78d35b89cf6e3aa282f12a1fb60a413261425b9a8fe025?color=5a5a5a) Anwendung des Satzes vom Nullprodukt ergibt
Anwendung des Satzes vom Nullprodukt ergibt  oder
oder 
 ist keine Lösung, da dies für
ist keine Lösung, da dies für  zu einer Ungeleichung führen würde.
Da
zu einer Ungeleichung führen würde.
Da  gilt, folgt:
gilt, folgt:
![\(\begin{array}[t]{rll}
ax+3&=& 0 &\quad \scriptsize \mid\;-3 \;\mid\;:a \\[5pt]
x&=& -\dfrac{3}{a}
\end{array}\)](https://mathjax.schullv.de/622c6b56e687db15828a77ef83ec60aa0a4096eb4c193fa6ef2f3926f7b1591e?color=5a5a5a) Auf die Anwendung der hinreichenden Bedingung für Extremstellen kann verzichtet werden, da in der Aufgabenstellung gegeben ist, dass alle Graphen von
Auf die Anwendung der hinreichenden Bedingung für Extremstellen kann verzichtet werden, da in der Aufgabenstellung gegeben ist, dass alle Graphen von  einen von
einen von  abhängigen Extrempunkt haben.
Der von
abhängigen Extrempunkt haben.
Der von  abhängige Extrempunkt liegt also an der Stelle
abhängige Extrempunkt liegt also an der Stelle  2. Schritt: Ortskurve
2. Schritt: Ortskurve  bestimmen
Um die Ortskurve zu berechnen, muss der
bestimmen
Um die Ortskurve zu berechnen, muss der  -Wert nach
-Wert nach  umgestellt und in
umgestellt und in  eingesetzt werden:
eingesetzt werden:
![\(\begin{array}[t]{rll}
x&=& -\dfrac{3}{a} \quad \scriptsize \mid\; \cdot a \\[5pt]
ax&=& -3 \quad \scriptsize \mid\; :x \\[5pt]
a&=& -\dfrac{3}{x}
\end{array}\)](https://mathjax.schullv.de/85838ee71cd5126d853f2cb6b4d1213eadf5c14f4f5178f7131b4d3ede8cde38?color=5a5a5a) Einsetzen in
Einsetzen in  liefert:
Die Gleichung der Ortskurve ist gegeben durch
liefert:
Die Gleichung der Ortskurve ist gegeben durch 
Lösung 2 – Analysis
a)
Anwendung der Produktregel:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/ff41f6445901bbd845c20a2708f1f88385eb76e0e79ca1dd8579769da6941a71?color=5a5a5a)
b)
Damit der Graph von  eine waagrechte Tangente besitzt, muss
eine waagrechte Tangente besitzt, muss  gelten.
gelten.
![\(\begin{array}[t]{rll}
f_a](https://mathjax.schullv.de/10716733d7388322d0ff35d08bae30e7ec649db11e1f6db95754ea31c0f73ed4?color=5a5a5a) Nach dem Satz vom Nullprodukt ist die Gleichung genau dann erfüllt, wenn einer der beiden Faktoren gleich null ist. Da
Nach dem Satz vom Nullprodukt ist die Gleichung genau dann erfüllt, wenn einer der beiden Faktoren gleich null ist. Da  für alle
für alle  muss gelten:
muss gelten:
![\(\begin{array}[t]{rll}
1-ax-a&=& 0 \quad \scriptsize \mid\; +ax \\[5pt]
1-a&=& ax \quad \scriptsize \mid\; :a \\[5pt]
\dfrac{1-a}{a} &=& x \\[5pt]
x &=& \dfrac{1-a}{a}
\end{array}\)](https://mathjax.schullv.de/92181974ca5818663e06167dd03cabf405cf2c3485bbd57bc903c44d2916d024?color=5a5a5a) Der Term ist für
Der Term ist für  nicht definiert. Der Graph von
nicht definiert. Der Graph von  besitzt also für alle
besitzt also für alle  eine waagrechte Tangente.
eine waagrechte Tangente.
Lösung 3 – Vektorielle Geometrie
a)
Der Vergleich der Koeffizienten von  ergibt:
ergibt:
![\(\begin{array}[t]{rll}
2a-1&=& 3 &\quad \scriptsize \mid\; +1 \\[5pt]
2a&=& 4 &\quad \scriptsize \mid\; :2 \\[5pt]
a &=& 2
\end{array}\)](https://mathjax.schullv.de/3a7be027eb950aa95010779babb5f7916a3ca72a1e4f9eb927213a7a8d03f0ad?color=5a5a5a) Der Koeffizientenvergleich von
Der Koeffizientenvergleich von  ergibt sofort
ergibt sofort  Diese Werte in
Diese Werte in  eingesetzt, ergeben:
eingesetzt, ergeben:
![\(\begin{array}[t]{rll}
(2\cdot 2-1)x+3y-z&=& 1 \\[5pt]
3x+3y-z&=& 1 \quad \scriptsize \mid\; +z \\[5pt]
3x+3y &=& 1+z
\end{array}\)](https://mathjax.schullv.de/b646000f9dee7856cc5bb73d8ede93cf75e79435e3bf97e08a323fce2dc8d569?color=5a5a5a) Dies entspricht der Ebenengleichung von
Dies entspricht der Ebenengleichung von  Damit gehört
Damit gehört  zur Ebenenschar
zur Ebenenschar 
b)
Für die  -Ebene gilt:
-Ebene gilt:  Für die Schnittgeraden muss daher gelten:
Für die Schnittgeraden muss daher gelten:  und
und  Zum Beispiel mit
Zum Beispiel mit  folgt:
folgt: 
 ist eine Gleichung der Geradenschar.
ist eine Gleichung der Geradenschar.
Lösung 4 – Vektorielle Geometrie
a)
1. Schritt: Einen Normalenvektor von  bestimmen
Ein Normalenvektor von
bestimmen
Ein Normalenvektor von  ist gegeben durch
ist gegeben durch 
 2. Schritt: Punkt aus
2. Schritt: Punkt aus  ermitteln
Der Mittelpunkt
ermitteln
Der Mittelpunkt  der Strecke
der Strecke  liegt in der Ebene
liegt in der Ebene 
![\(\begin{array}[t]{rll}
\overrightarrow{OM}&=&\overrightarrow{OP}+\dfrac{1}{2}\cdot \overrightarrow{PQ} & \\[5pt]
&=&\pmatrix{1\\2\\3}+\dfrac{1}{2}\cdot \pmatrix{6\\0\\8} & \\[5pt]
&=&\pmatrix{4\\2\\7}
\end{array}\)](https://mathjax.schullv.de/de42f0308592c2f9444b185dabde40a002f206b75e2a1441c46561dc31332e0b?color=5a5a5a) 3. Schritt:
3. Schritt:  in
in  einsetzen
einsetzen
![\(\begin{array}[t]{rll}
E: 6\cdot x_1+8\cdot x_3&=&c & \\[5pt]
6\cdot 4+8\cdot 7&=&c & \\[5pt]
80&=&c
\end{array}\)](https://mathjax.schullv.de/8050a57ed532b06c9b0eba69d227a47f5011f7d32a42383a98862b771a71bea6?color=5a5a5a) Eine Gleichung für
Eine Gleichung für  ist somit gegeben durch:
ist somit gegeben durch:

b)
Lösung 5 – Stochastik
a)
Für den Fall, dass Paula mindestens zwei rote Gummibärchen isst, gibt es 4 Möglichkeiten:
 rotes Gummibärchen
rotes Gummibärchen
 grünes Gummibärchen
grünes Gummibärchen



 Somit ergibt sich für das Ereignis folgende Wahrscheinlichkeit:
Somit ergibt sich für das Ereignis folgende Wahrscheinlichkeit:

b)
Ereignis  : orangenes Gummibärchen wird zuerst gezogen
: orangenes Gummibärchen wird zuerst gezogen
 Ereignis
Ereignis  : orangenes Gummibärchen wird als zweites gezogen
: orangenes Gummibärchen wird als zweites gezogen
 Anzahl
Anzahl  der Gummibärchen bestimmen:
Es befinden sich somit
der Gummibärchen bestimmen:
Es befinden sich somit  Gummibärchen im Behälter.
Gummibärchen im Behälter.
Lösung 6 – Stochastik
a)
b)
Wahrscheinlichkeitsverteilung  Diagramm III
Da in dem Behälter mehr schwarze als weiße Kugeln enthalten sind, muss die Verteilung asymmetrisch sein. Dies ist nur im Diagramm III der Fall.
Wahrscheinlichkeitsverteilung
Diagramm III
Da in dem Behälter mehr schwarze als weiße Kugeln enthalten sind, muss die Verteilung asymmetrisch sein. Dies ist nur im Diagramm III der Fall.
Wahrscheinlichkeitsverteilung  Diagramm II
Betrachten eines Beispielwertes:
Diagramm II
Betrachten eines Beispielwertes:
![\(\begin{array}[t]{rll}
P(X=3)&=& P({(1;2),(2;1)}) & \\[5pt]
&=& \dfrac{2}{36}
\end{array}\)](https://mathjax.schullv.de/63726b7c760df8f2f106062238b36307677878a0d732b18d80972ba6dd2c66bd?color=5a5a5a) Da die Wahrscheinlichkeit
Da die Wahrscheinlichkeit  (in
(in  berechnet) nicht doppelt so groß wie
berechnet) nicht doppelt so groß wie  ist, kann das Diagramm I ausgeschlossen werden. Die Wahrscheinlichkeitsverteilung von
ist, kann das Diagramm I ausgeschlossen werden. Die Wahrscheinlichkeitsverteilung von  wird dementsprechend im Diagramm II dargestellt.
wird dementsprechend im Diagramm II dargestellt.