Aufgabe 1
Aufgabenstellung:
In einer Studie zum Spracherwerb von Kindern ist untersucht worden, wie sich die Länge gesprochener Sätze (kurz: Satzlänge) mit dem Alter der Kinder entwickelt.
Ein Sprachforscher modelliert mit einer Funktion die momentane Änderungsrate, mit der sich die durchschnittliche Satzlänge
die momentane Änderungsrate, mit der sich die durchschnittliche Satzlänge der Kinder, die an der Studie teilgenommen haben, im Alter von
der Kinder, die an der Studie teilgenommen haben, im Alter von  Jahren bis
Jahren bis  Jahren verändert. Dazu verwendet er für
Jahren verändert. Dazu verwendet er für  die Gleichung
die Gleichung
 ,
, 
Dabei wird als Maßzahl zur Maßeinheit
als Maßzahl zur Maßeinheit  Jahr und
Jahr und  als Maßzahl zur Maßeinheit
als Maßzahl zur Maßeinheit  Wort pro Jahr aufgefasst.
Wort pro Jahr aufgefasst.
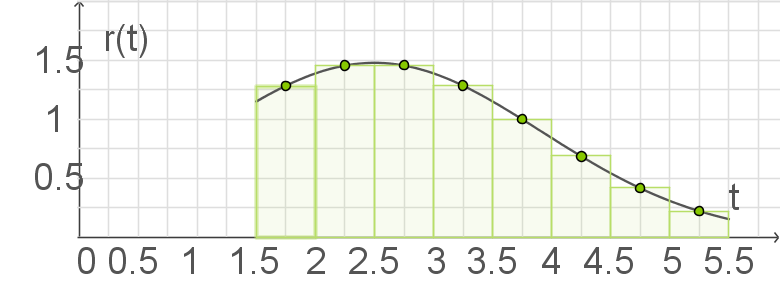
Der Graph von im Bereich
im Bereich  ist in Abbildung 1 dargestellt.
ist in Abbildung 1 dargestellt.
 Im Folgenden wird die durchschnittliche Satzlänge der Kinder, die an der Studie teilgenommen haben, kurz als Satzlänge bezeichnet.
Im Folgenden wird die durchschnittliche Satzlänge der Kinder, die an der Studie teilgenommen haben, kurz als Satzlänge bezeichnet.













 Bildnachweise [nach oben]
Bildnachweise [nach oben]
Ein Sprachforscher modelliert mit einer Funktion
Dabei wird
Der Graph von
a)
(1)
Berechne den Funktionswert von  an der Stelle
an der Stelle  und interpretiere diesen Wert im Sachzusammenhang.
und interpretiere diesen Wert im Sachzusammenhang.
(2P)
(2)
Für die Funktion  gilt die Aussage:
gilt die Aussage:
 für alle
für alle  .
Interpretiere die Bedeutung dieser Aussage im Sachzusammenhang.
.
Interpretiere die Bedeutung dieser Aussage im Sachzusammenhang.
(3P)
(3)
Weise rechnerisch nach, dass im gegebenen Modell im Alter von  Jahren die größte momentane Änderungsrate der Satzlänge vorliegt.
Jahren die größte momentane Änderungsrate der Satzlänge vorliegt.
(6P)
(4)
Ermittle das Alter zwischen  und
und  Jahren, in dem die momentane Änderungsrate der Satzlänge am schnellsten abnimmt.
Jahren, in dem die momentane Änderungsrate der Satzlänge am schnellsten abnimmt.
(7P)
b)
In der Studie ist bei Kindern im Alter von  Jahren eine Satzlänge von
Jahren eine Satzlänge von  Wörtern beobachtet worden.
Wörtern beobachtet worden.
(1)
Interpretiere die Bedeutung der Terme  und
und  im Sachzusammenhang.
im Sachzusammenhang.
(4P)
Die konkrete Ermittlung eines Funktionsterms einer Stammfunktion von  mit Hilfe eines Integrationsverfahrens ist nicht möglich. Daher wird der Wert des Integrals
mit Hilfe eines Integrationsverfahrens ist nicht möglich. Daher wird der Wert des Integrals  durch ein numerisches Verfahren bestimmt. In Abbildung 2 ist dieses Verfahren veranschaulicht.
durch ein numerisches Verfahren bestimmt. In Abbildung 2 ist dieses Verfahren veranschaulicht.
(2)
Beschreibe kurz das Vorgehen bei diesem numerischen Verfahren.
(4P)
(3)
Berechne mit diesem numerischen Verfahren einen Nährungswert für den Term  .
.
(5P)
c)
Für  ist die Funktion
ist die Funktion  definiert durch die Gleichung
definiert durch die Gleichung  .
.
(1)
Interpretiere, welche Bedeutung die Funktion  im Sachzusammenhang hat.
im Sachzusammenhang hat.
(2P)
(2)
Begründe, warum für die Ableitung der Funktion  mit
mit  gilt:
gilt:
 [Du kannst davon ausgehen, dass es eine Stammfunktion
[Du kannst davon ausgehen, dass es eine Stammfunktion  von
von  gibt. Wie bereits in b) angegeben, ist die konkrete Ermittlung eines Funktionsterms von
gibt. Wie bereits in b) angegeben, ist die konkrete Ermittlung eines Funktionsterms von  mit Hilfe eines Integrationsverfahrens aber nicht möglich.]
mit Hilfe eines Integrationsverfahrens aber nicht möglich.]
(3P)
Für die Funktion  wird folgende Berechnung durchgeführt, die von dir in der Teilaufgabe (3) interpretiert werden soll:
I
wird folgende Berechnung durchgeführt, die von dir in der Teilaufgabe (3) interpretiert werden soll:
I 

 .
.
II .
.
II
(3)
Interpretiere die Lösung  der Gleichung
der Gleichung  (siehe I) unter Berücksichtigung von II im Sachzusammenhang.
(siehe I) unter Berücksichtigung von II im Sachzusammenhang.
(3P)
d)
Einige Forscher gehen davon aus, dass bei zweisprachig aufwachsenden Kindern eine verzögerte Sprachentwicklung auftritt.
Zur Modellierung der durchschnittlichen Satzlänge von zweisprachig aufwachsenden Kindern im Alter von Jahren bis
Jahren bis  Jahren verwendet der Sprachforscher für
Jahren verwendet der Sprachforscher für  die Funktion
die Funktion  mit der Gleichung
mit der Gleichung
 ,
,  .
.
Zur Modellierung der durchschnittlichen Satzlänge von zweisprachig aufwachsenden Kindern im Alter von
(1)
Der Graph der Funktion  geht durch eine Verschiebung aus dem Graphen der Funktion
geht durch eine Verschiebung aus dem Graphen der Funktion  hervor.
hervor.
Zeichne in Abbildung 1 den Graphen von ein und ermittle anhand deiner Zeichnung die Verschiebung.
ein und ermittle anhand deiner Zeichnung die Verschiebung.
Zeichne in Abbildung 1 den Graphen von
(5P)
(2)
Prüfe nun rechnerisch, ob sich bei der von dir ermittelten Verschiebung der Funktionsterm von  aus dem Funktionsterm von
aus dem Funktionsterm von  ergibt.
ergibt.
(2P)
(3)
Für die zweisprachig aufwachsenden Kinder geht der Sprachforscher davon aus, dass die durchschnittliche Satzlänge von  Wörtern statt im Alter von
Wörtern statt im Alter von  Jahren erst im Alter von
Jahren erst im Alter von  Jahren vorliegt.
Jahren vorliegt.
Ermittle unter dieser Voraussetzung, welcher Unterschied im Alter von Jahren zwischen der Satzlänge der Kinder, die an der Studie teilgenommen haben, und der Satzlänge der zweisprachig aufgewachsenen Kinder besteht.
Jahren zwischen der Satzlänge der Kinder, die an der Studie teilgenommen haben, und der Satzlänge der zweisprachig aufgewachsenen Kinder besteht.
Ermittle unter dieser Voraussetzung, welcher Unterschied im Alter von
(4P)
© 2016 - SchulLV.
© 2016 - SchulLV.
a)
(1)
(2)
(3)
- Notwendige Bedingung:
- Hinreichende Bedingung:
- Bilde die erste und zweite Ableitung von
- Prüfe die notwendige Bedingung
- Prüfe die hinreichende Bedingung
(4)
- Notwendige Bedingung:
- Hinreichende Bedingung:
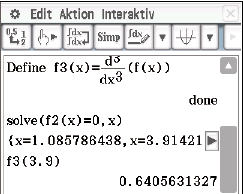
- Definiere die Funktion
und die zweite und dritte Ableitung in dem CAS
- Prüfe die notwendige und die hinreichende Bedingung
 Abb. 1: Funktionen definieren.
Abb. 1: Funktionen definieren.
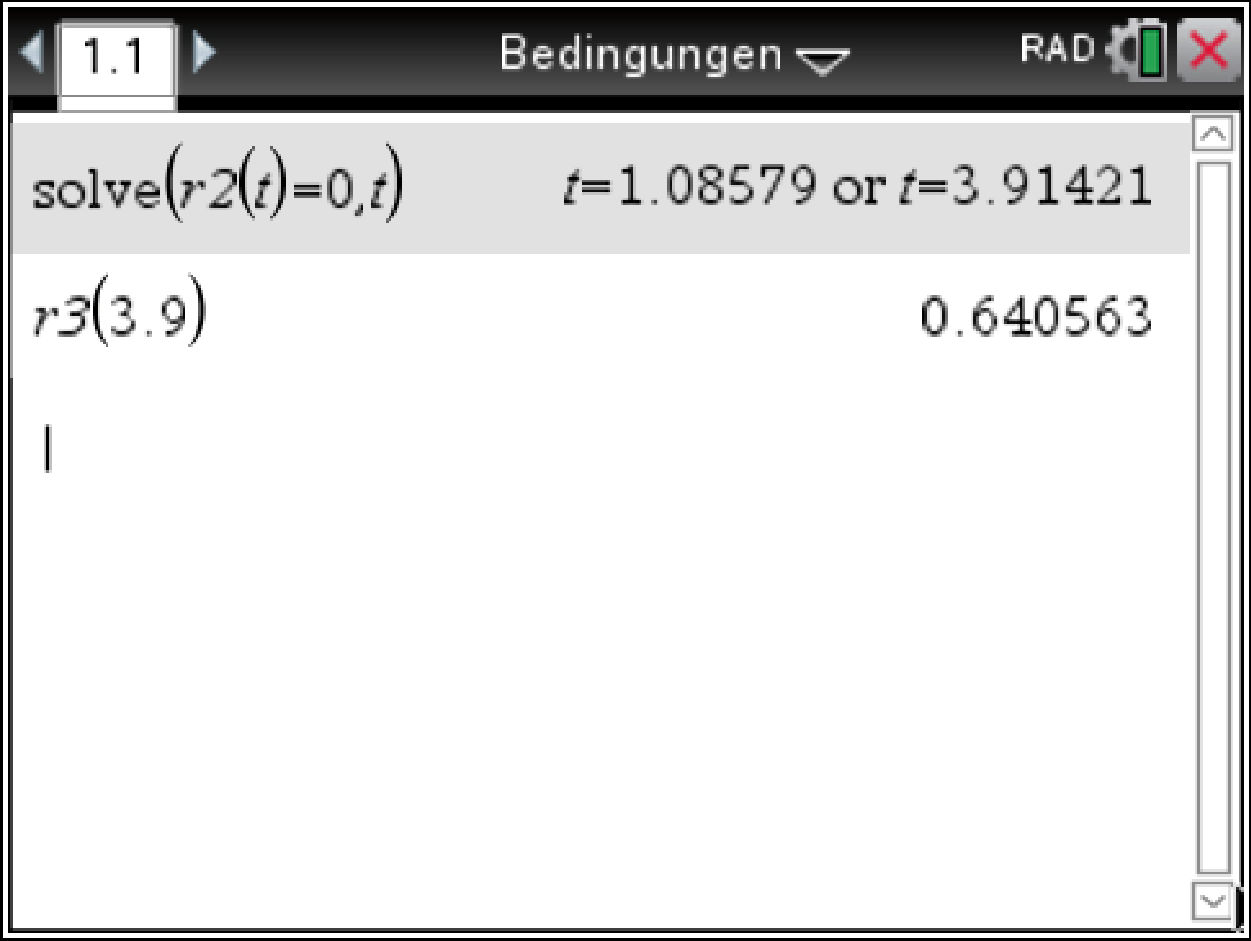
Du erhältst als Lösung die Werte  und
und  . Der Wert von
. Der Wert von  liegt nicht in dem Intervall
liegt nicht in dem Intervall ![\([1,5;5,5]\)](https://mathjax.schullv.de/97784ff3cf62ca6b596d294d32c9917c7dae1c2ed954f9ccada05f21941ef066?color=5a5a5a) . Somit liegt die gesuchte potentielle Wendestelle an der Stelle
. Somit liegt die gesuchte potentielle Wendestelle an der Stelle  . Setze diesen Wert in die dritte Ableitung von
. Setze diesen Wert in die dritte Ableitung von  ein, um die hinreichende Bedingung zu prüfen.
Die dritte Ableitung
ein, um die hinreichende Bedingung zu prüfen.
Die dritte Ableitung  ist an der Stelle
ist an der Stelle  ungleich Null. Die Funktion
ungleich Null. Die Funktion  hat daher an der Stelle
hat daher an der Stelle  eine Wendestelle.
eine Wendestelle.
b)
(1)
(2)
(3)
c)
(1)
(2)
(3)
d)
(1)
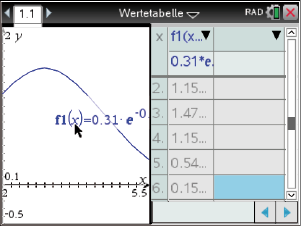 Abb. 3: Wertetabelle.
Abb. 3: Wertetabelle.
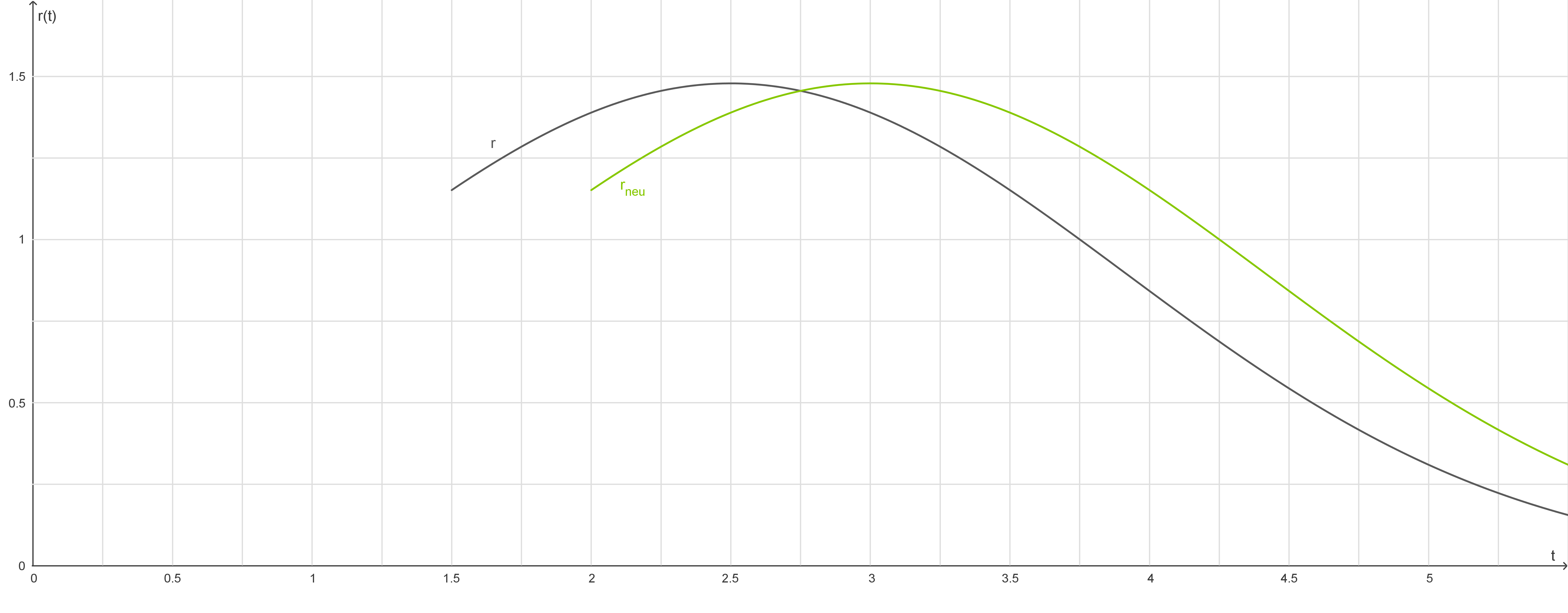 Abb. 4: Abbildung der Graphen.
Abb. 4: Abbildung der Graphen.
(2)
(3)
 Abb. 5: Unterschied der Satzlänge.
Abb. 5: Unterschied der Satzlänge.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
a)
(1)
(2)
(3)
- Notwendige Bedingung:
- Hinreichende Bedingung:
- Bilde die erste und zweite Ableitung von
- Prüfe die notwendige Bedingung
- Prüfe die hinreichende Bedingung
(4)
- Notwendige Bedingung:
- Hinreichende Bedingung:
- Definiere die Funktion
und die zweite und dritte Ableitung in dem CAS
- Prüfe die notwendige und die hinreichende Bedingung
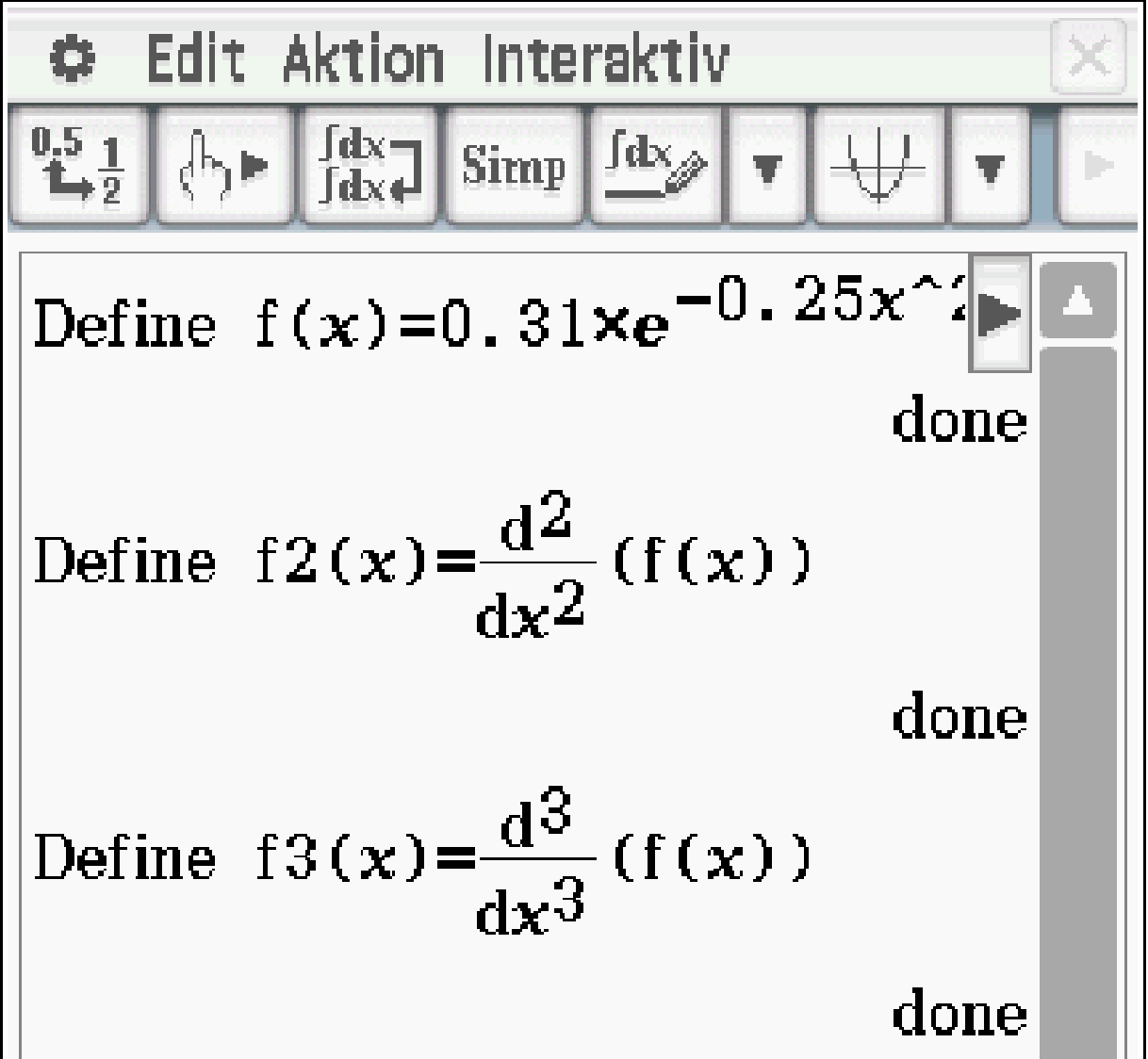 Abb. 1: Funktionen definieren.
Abb. 1: Funktionen definieren.
b)
(1)
(2)
(3)
c)
(1)
(2)
(3)
d)
(1)
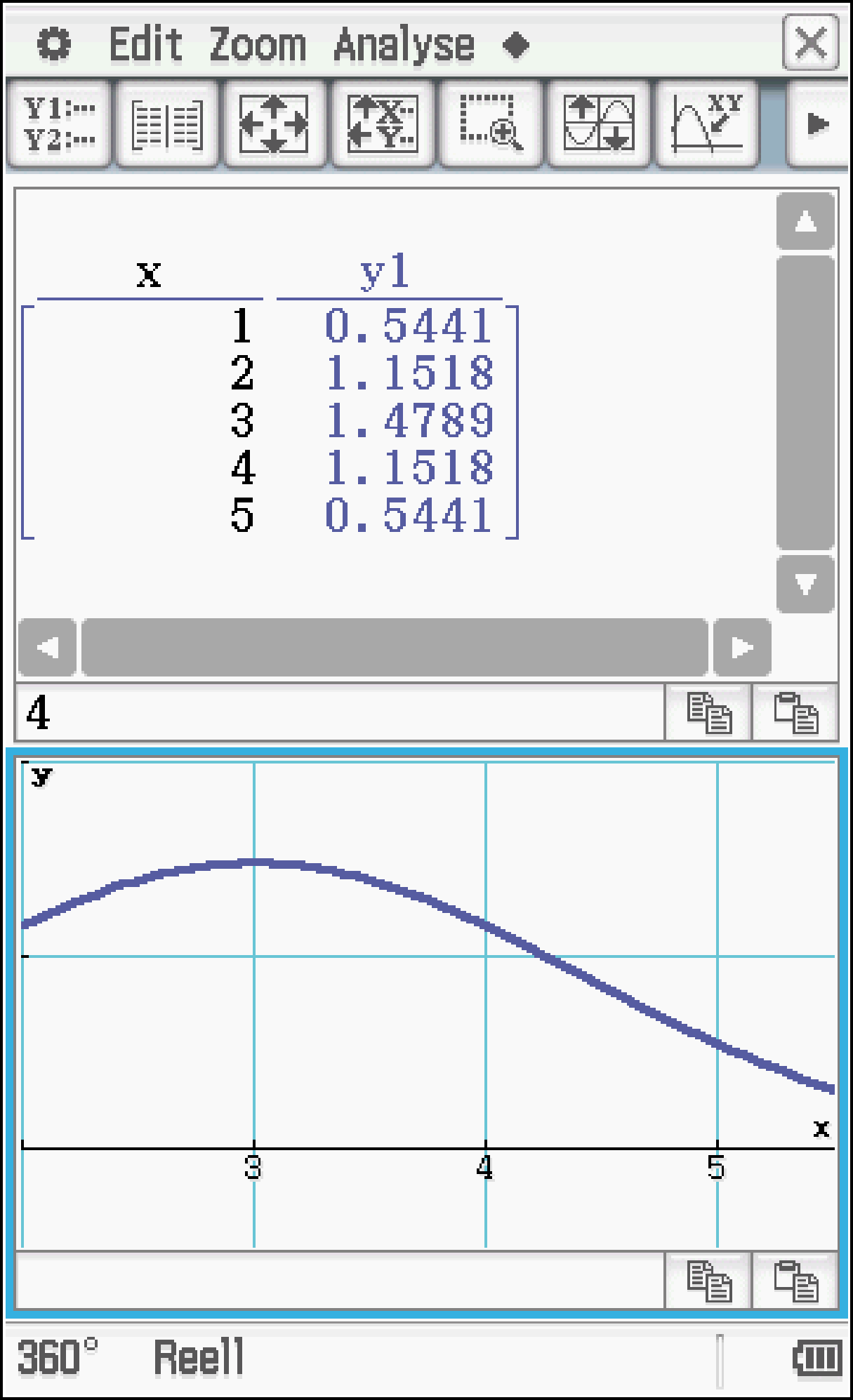 Abb. 3: Wertetabelle.
Abb. 3: Wertetabelle.
 Abb. 4: Abbildung der Graphen.
Abb. 4: Abbildung der Graphen.
(2)
(3)
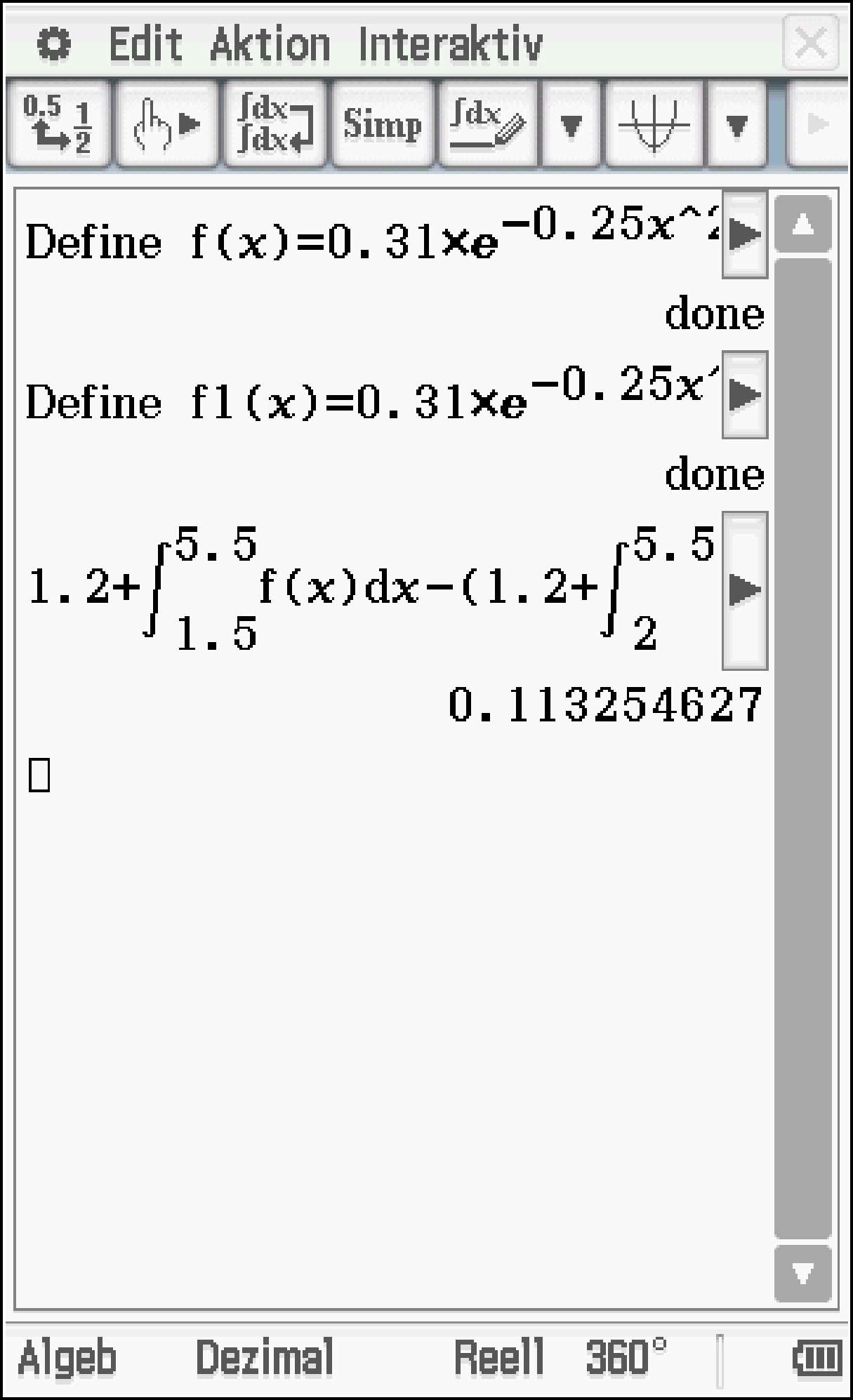 Abb. 5: Unterschied der Satzlänge.
Abb. 5: Unterschied der Satzlänge.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.