Aufgabe 5

Ein Unternehmen stellt Kunststoffteile her. Erfahrungsgemäß sind $4\,\%$ der hergestellten Teile fehlerhaft. Die Anzahl fehlerhafter Teile unter zufällig ausgewählten kann als binomialverteilt angenommen werden.

$\,$

(1)

$800$ Kunststoffteile werden zufällig ausgewählt.
Bestimme für die folgenden Ereignisse jeweils die Wahrscheinlichkeit:

$A:$

"Genau $30$ der Teile sind fehlerhaft."

$B:$

"Mindestens $5\,\%$ der Teile sind fehlerhaft."

(5 Punkte)

$\,$

(2)

Ermittle, wie viele Kunststoffteile mindestens zufällig ausgewählt werden müssen, damit davon mit einer Wahrscheinlichkeit von mindestens $95\,\%$ mindestens $100$ Teile keinen Fehler haben.

(5 Punkte)

$\,$

Die Kunststoffteile werden aus Kunststoffgranulat hergestellt. Nach einem Wechsel des Granulats vermutet der Produktionsleiter, dass sich der Anteil der fehlerhaften Teile reduziert hat. Um einen Anhaltspunkt dafür zu gewinnen, ob die Vermutung gerechtfertigt ist, soll die Nullhypothese "Der Anteil der fehlerhaften Teile beträgt mindestens $4\,\%$ " auf der Grundlage einer Stichprobe von $500$ Teilen auf einem Signifikanzniveau von $5\,\%$ getestet werden.

$\,$

(3)

Bestimme die zugehörige Entscheidungsregel.

(6 Punkte)

$\,$

(4)

Das neue Granulat ist teurer als das vorherige.
Gib an, welche Überlegung zur Wahl der Nullhypothese geführt haben könnte, und begründe deine Angabe.

(4 Punkte)

$\,$

(5)

Interpretiere den Fehler 2. Art im Sachzusammenhang und bestimme seine Wahrscheinlichkeit, wenn in Wirklichkeit nur $2\,\%$ der Teile fehlerhaft sind.

(5 Punkte)

Für ein Spiel wird ein Glücksrad verwendet, das drei farbige Sektoren hat. Der Tabelle können die Farben der Sektoren und die Größen der zugehörigen Mittelpunktswinkel entnommen werden.

Farbe	Mittelpunktswinkel
Blau	$180^{\circ}$
Rot	$120^{\circ}$
Grün	$60^{\circ}$

Für einen Einsatz von $5$ Euro darf ein Spieler das Glücksrad dreimal drehen. Erzielt der Spieler dreimal die gleiche Farbe, werden ihm $10$ Euro ausgezahlt.
Erzielt er drei verschiedene Farben, wird ein anderer Betrag ausgezahlt. In allen anderen Fällen erfolgt keine Auszahlung.

Die Wahrscheinlichkeit dafür, dass dreimal die gleiche Farbe erzielt wird, ist $\dfrac{1}{6}.$

$\,$

(1)

Zeige, dass die Wahrscheinlichkeit dafür, dass drei verschiedene Farben erzielt werden, ebenfalls $\dfrac{1}{6}$ beträgt.

(4 Punkte)

$\,$

(2)

Bei dem Spiel ist zu erwarten, dass sich die Einsätze der Spieler und die Auszahlungen auf lange Sicht ausgleichen.
Bestimme den Betrag, der ausgezahlt wird, wenn drei verschiedene Farben erscheinen.

(5 Punkte)

$\,$

(3)

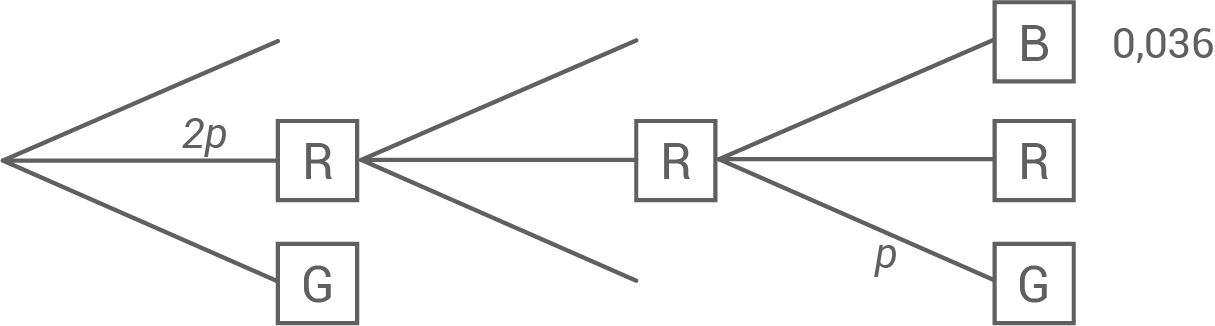
Die Größen der Sektoren werden geändert. Dabei wird der blaue Sektor vergrößert. Die Abbildung zeigt einen Teil eines Baumdiagramms, das für das geänderte Glücksrad die drei Drehungen beschreibt. Ergänzend ist für einen Pfad die zugehörige Wahrscheinlichkeit angegeben.

Abbildung 1

Bestimme die Größe des zum blauen Sektor gehörenden Mittelpunktswinkels.

(6 Punkte)

(1)

$\blacktriangleright$ Wahrscheinlichkeiten bestimmen

Betrachtet wird die Zufallsgröße $X,$ die die Anzahl der fehlerhaften Teile in einer zufälligen Stichprobe von $800$ Kunststoffteilen beschreibt. Diese kann laut Aufgabenstellung als binomialverteilt mit $n=800$ und $p=0,04$ angenommen werden.

Mithilfe des CAS kann dann die gesuchte Wahrscheinlichkeit mit dem binomPdf- bzw. binomCdf-Befehl bestimmt werden.

$\blacktriangleright$ TI nspire CAS

menu $\to$ 5 $\to$ 5 $\to$ D: Binomial Pdf / E: Binomial Cdf

$\blacktriangleright$ Casio Classpad II

Interaktiv $\to$ Verteilungsfunktionen $\to$ Diskret $\to$ binomial PDf / binomial CDf

Für Ereignis $A$ ergibt sich mit dem Binomial Pdf-Befehl:

$P(A)\approx 6,93\,\%$

Vollständige Lösung anzeigen

Für Ereignis $B$ muss zuerst berechnet werden, wie viel $5\,\%$ sind:

$0,05 \cdot 800 = 40$

Mit dem Binomial Cdf-Befehl folgt daher:

$P(B)\approx 9,12\,\%$

Vollständige Lösung anzeigen

$\,$

(2)

$\blacktriangleright$ Mindestanzahl berechnen

Betrachtet wird die Zufallsgröße $X_n,$ die die Anzahl der fehlerfreien Teile in einer zufälligen Stichprobe von $n$ Kunststoffteilen beschreibt. Diese kann laut Aufgabenstellung als binomialverteilt mit unbekanntem $n$ und $p=0,96$ angenommen werden.
Gesucht ist dann das kleinste $n,$ sodass gerade noch $P(X_n \geq 100) \geq 0,95$ gilt.

Berechne dazu für verschiedene $n\geq 100$ den Wert $P(X_n \geq 100).$
Mit dem CAS erhältst du:

$\begin{array}[t]{rll} P(X_{107}\geq 100)&\approx& 0,93 \\[5pt] P(X_{108}\geq 100)&\approx& 0,97 \\[5pt] \end{array}$

Es müssen also mindestens $108$ Kunststoffteile ausgewählt werden, um mit einer Wahrscheinlichkeit von mindestens $95\,\%$ mindestens $100$ fehlerfreie zu erhalten.

$\,$

(3)

$\blacktriangleright$ Entscheidungsregel bestimmen

Betrachtet wird die Zufallsgröße $X_p,$ die die Anzahl der fehlerhaften Teile in einer zufälligen Stichprobe von $500$ Kunststoffteilen beschreibt. Diese kann als binomialverteilt mit $n=500$ und unbekanntem $p$ angenommen werden.

Getestet wird die Nullhypothese $H_0:\quad p \geq 0,04$

mit der Gegenhypothese $H_1:\quad p \lt 0,04$

auf einem Signifikanzniveau von $5\,\%.$

Trifft die Nullhypothese im Extremfall zu, ist $p=0,04.$ Gesucht ist nun die größte Anzahl fehlerhafter Teile $k,$ die in der Stichprobe gefunden werden darf, sodass die Nullhypothese gerade noch abgelehnt wird.
Mit dem Signifikanzniveau ergibt sich die Gleichung:

$P(X_{0,04} \leq k) \leq 0,05$

Mit deinem CAS erhältst du durch systematisches Probieren oder das Anlegen einer Tabelle für verschiedene Werte von $k$ folgende Wahrscheinlichkeiten:

$\begin{array}[t]{rll} P(X_{0,04}\leq 12)&\approx& 0,036 \\[5pt] P(X_{0,04}\leq 13)&\approx& 0,062 \\[5pt] \end{array}$

Sind also von den $500$ Teilen höchstens $12$ fehlerhaft, wird die Nullhypothese verworfen und man kann auf dem Signifikanzniveau von $5\,\%$ davon ausgehen, dass sich der Anteil der fehlerhaften Teile durch das neue Granulat verbessert hat.

$\,$

(4)

$\blacktriangleright$ Hintergrund der Hypothese angeben

Durch die Wahl der Nullhypothese $H_0: p\geq 0,04$ und des Signifikanzniveaus von $5\,\%$ wird die Wahrscheinlichkeit dafür, dass man fälschlicherweise davon ausgeht, dass das neue Granulat besser ist, obwohl es eigentlich eine schlechtere oder gleichschlechte Fehlerquote hat wie das alte, auf maximal $5\,\%$ begrenzt.
Das Unternehmen möchte also möglichst verhindern, dass das alte Granulat durch das neue teurere ausgetauscht wird, obwohl die Fehlerquote nicht geringer ist. In dem Fall, würde sich die Qualität der Produktion nicht verbessern, aber die Kosten würden ansteigen.

$\,$

(5)

$\blacktriangleright$ Fehler interpretieren

Der Fehler 2. Art wird begangen, wenn die Nullhypothese fälschlicherweise nicht abgelehnt wird, obwohl in Wirklichkeit eine andere, der Gegenhypothese entsprechende, Wahrscheinlichkeit gilt.
Beim vorliegenden Test lautet die Nullhypothese „Der Anteil der fehlerhaften Teile beträgt nach dem Wechsel des Granulats mindestens $4\,\%.$ “.
Hierbei bedeutet der Fehler 2. Art also, fälschlicherweise davon auszugehen, dass das neue Granulat eine mindestens genauso hohe Fehlerquote aufweist wie das alte, obwohl sich der Anteil der fehlerhaften Teile mit dem neuen Granulat in der Wirklichkeit eigentlich reduziert hat.

$\blacktriangleright$ Wahrscheinlichkeit bestimmen

Betrachtet wird die Zufallsvariable $X_{0,02},$ die die Anzahl der fehlerhaften Teile unter $500$ zufällig ausgewählten Teilen beschreibt, die mit dem neuen Granulat hergestellt wurden. Beträgt der Anteil der fehlerhaften Teile in Wirklichkeit nur $2\,\%,$ ist $X_{0,02}$ binomialverteilt mit $n=500$ und $p = 0,02.$
Die Nullhypothese wird trotzdem nicht abgelehnt, wenn $X_{0,02} \gt 12$ ist. Mit dem Gegenereignis und dem CAS ergibt sich:

$P(X_{0,02} \gt 12)\approx 0,2065$

Vollständige Lösung anzeigen

Beträgt die Wahrscheinlichkeit für ein fehlerhaftes Teil bei dem neuen Granulat tatsächlich nur $2\,\%,$ ist die Wahrscheinlichkeit für den Fehler 2. Art ca. $20,65\,\%.$

(1)

$\blacktriangleright$ Wahrscheinlichkeit für drei verschiedene Farben nachweisen

Die Wahrscheinlichkeiten für die einzelnen Farben sind:

$\begin{array}[t]{rll} P(\text{Blau})&=& \dfrac{180^{\circ}}{360^{\circ}} \\[5pt] &=& \frac{1}{2} \\[10pt] P(\text{Rot})&=& \dfrac{120^{\circ}}{360^{\circ}} \\[5pt] &=& \frac{1}{3} \\[10pt] P(\text{Grün})&=& \dfrac{60^{\circ}}{360^{\circ}} \\[5pt] &=& \frac{1}{6} \\[10pt] \end{array}$

Jede Farbe soll genau einmal gedreht werden. Das Experiment kann mit dem Ziehen mit Zurücklegen verglichen werden. Verwende die Pfadregeln. Die Anzahl der Pfade entspricht der Anzahl der möglichen Permutationen von drei Elementen, kann also mithilfe der Fakultät berechnet werden.

$... = \frac{1}{6}$

Vollständige Lösung anzeigen

$\,$

(2)

$\blacktriangleright$ Auszahlung berechnen

Der erwartete Gewinn soll auf Null herauskommen. Betrachtet wird die Zufallsgröße $G,$ die den zufälligen Gewinn des Spielers beschreibt. Mit $a$ wird der Betrag bezeichnet, der ausgezahlt wird, wenn drei verschiedene Farben erscheinen.

$a= 20\,€$

Vollständige Lösung anzeigen

Wenn drei verschiedene Farben erscheinen, werden $20\,€$ ausgezahlt.

$\,$

(3)

$\blacktriangleright$ Die Weite des Mittelpunktswinkels bestimmen

Für die Wahrscheinlichkeiten der drei Sektoren gilt laut Baumdiagramm:

grün: $p$
rot: $2p$
blau: $1-p-2p = 1-3p$

Mit der Pfadmultiplikationsregel folgt aus der angegebenen Pfadwahrscheinlichkeit eine Gleichung. Diese kannst du mit dem solve-Befehl deines CAS lösen.

$\begin{array}[t]{rll} p_1&\approx& -0,085 \\[5pt] p_2&\approx& 0,118 \\[5pt] p_3&=& 0,3 \end{array}$

Vollständige Lösung anzeigen

$p_1$ ist negativ und kommt daher nicht infrage.
Für $p_2$ folgt für die Wahrscheinlichkeit von blau: $1-3p_2 \approx 0,646.$
Für $p_3$ folgt entsprechend für die Wahrscheinlichkeit von blau: $1-3p_3 = 0,1$

Da der Mittelpunktswinkel des blauen Sektors vergrößert werden soll, muss die Wahrscheinlichkeit von blau größer als $0,5$ sein. Die einzige mögliche Lösung ist also $p_2 \approx 0,118$ mit der Wahrscheinlichkeit $0,646$ für blau. Der zugehörige Mittelpunktswinkel ist dann:

$360^{\circ}\cdot 0,646 = 232,56^{\circ}$

Der Mittelpunktswinkel des blauen Sektors hat die Weite $232,56^{\circ}.$