Aufgabe 2
a)
Auf einer Autobahn entsteht morgens an einer Baustelle häufig ein Stau. An einem bestimmten Tag entsteht der Stau um 06:00 Uhr und löst sich bis 10:00 Uhr vollständig auf. Für diesen Tag kann die momentane Änderungsrate der Staulänge von der Entstehung bis zur Auflösung des Staus mithilfe der in  definierten Funktion
definierten Funktion  mit
mit
 beschrieben werden. Dabei gibt
beschrieben werden. Dabei gibt  die nach 06:00 Uhr vergangene Zeit in Stunden und
die nach 06:00 Uhr vergangene Zeit in Stunden und  die momentane Änderungsrate der Staulänge in Kilometer pro Stunde an.
die momentane Änderungsrate der Staulänge in Kilometer pro Stunde an.
 die in
die in  definierte Funktion
definierte Funktion  mit
mit
 von Bedeutung.
von Bedeutung.
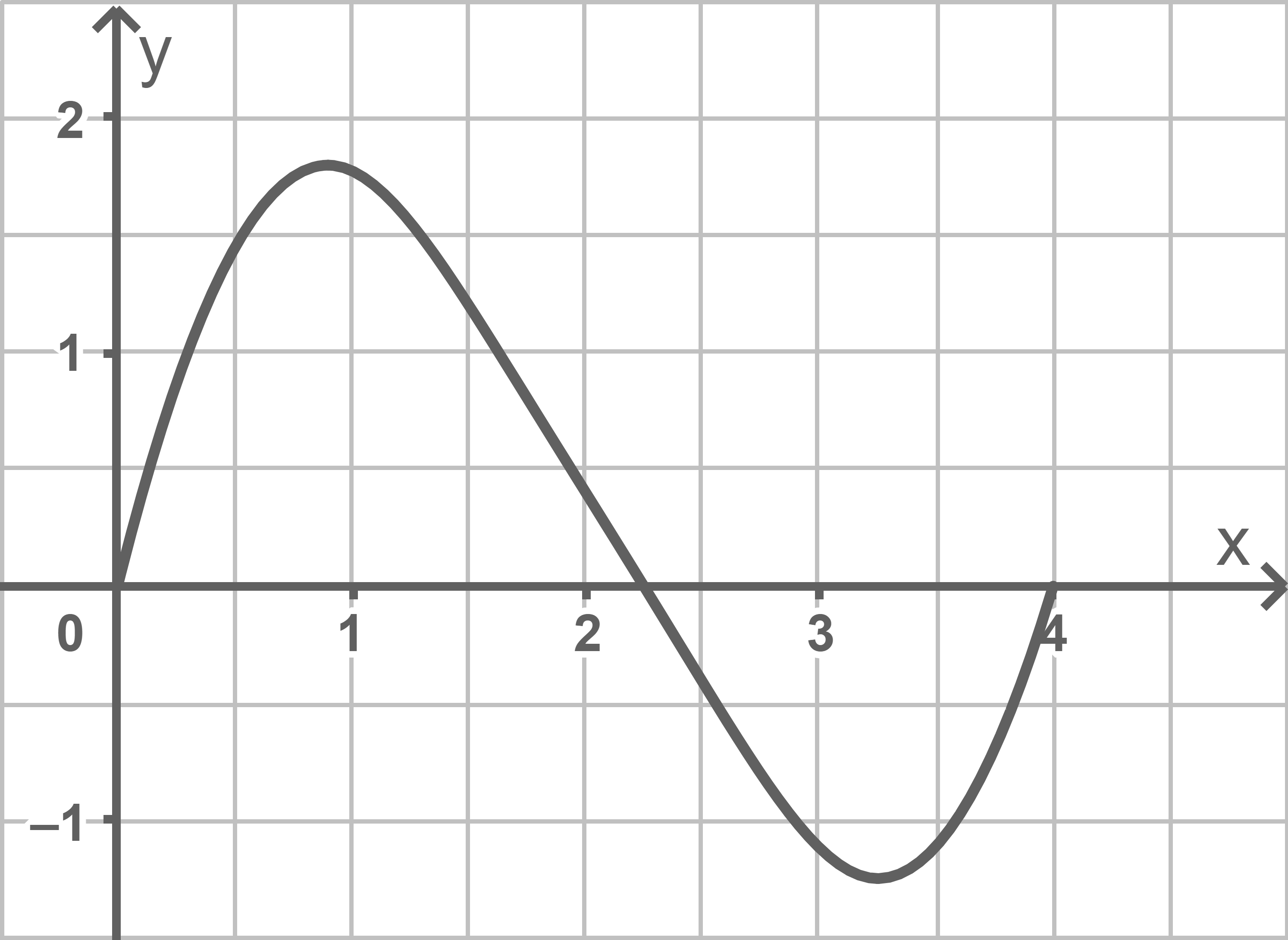 Um 07:30 Uhr hat der Stau eine bestimmte Länge. Es gibt einen anderen Zeitpunkt, zu dem der Stau die gleiche Länge hat.
Markiere diesen Zeitpunkt näherungsweise in der Abbildung 1 und begründe dein Vorgehen.
Um 07:30 Uhr hat der Stau eine bestimmte Länge. Es gibt einen anderen Zeitpunkt, zu dem der Stau die gleiche Länge hat.
Markiere diesen Zeitpunkt näherungsweise in der Abbildung 1 und begründe dein Vorgehen.
(1)
Nenne die Zeitpunkte, zu denen die momentane Änderungsrate der Staulänge den Wert null hat, und begründe anhand der Struktur des Funktionsterms von  dass es keine weiteren solcher Zeitpunkte gibt.
dass es keine weiteren solcher Zeitpunkte gibt.
(2)
Es gilt 
Gib die Bedeutung dieser Tatsache im Sachzusammenhang an.
Gib die Bedeutung dieser Tatsache im Sachzusammenhang an.
(3)
Bestimme den Zeitpunkt, zu dem die Staulänge am stärksten zunimmt.
Zeige, dass der zugehörige Wert der momentanen Änderungsrate zwischen  und
und  liegt.
liegt.
(4)
Gib den Zeitpunkt an, zu dem der Stau am längsten ist. Begründe deine Angabe.
Im Sachzusammenhang ist neben der Funktion
(5)
Begründe, dass die folgende Aussage richtig ist:
Die Staulänge in Kilometern kann für jeden Zeitpunkt von 06:00 Uhr bis 10:00 Uhr durch die Funktion  angegeben werden.
Bestätige rechnerisch, dass sich der Stau um 10:00 Uhr vollständig aufgelöst hat.
angegeben werden.
Bestätige rechnerisch, dass sich der Stau um 10:00 Uhr vollständig aufgelöst hat.
(6)
Berechne die Zunahme der Staulänge von 06:30 Uhr bis 08:00 Uhr und bestimme für diesen Zeitraum die durchschnittliche Änderungsrate der Staulänge.
(7)
Bestimme denjenigen Zeitpunkt zwischen 06:00 Uhr und 10:00 Uhr, zu dem die Staulänge  geringer ist als eine Stunde vorher.
geringer ist als eine Stunde vorher.
(8)
Für einen anderen Tag wird die momentane Änderungsrate der Staulänge für den Zeitraum von 06:00 Uhr bis 10:00 Uhr durch den in der Abbildung 1 gezeigten Graphen dargestellt. Dabei ist  die nach 06:00 Uhr vergangene Zeit in Stunden und
die nach 06:00 Uhr vergangene Zeit in Stunden und  die momentane Änderungsrate in Kilometer pro Stunde.
die momentane Änderungsrate in Kilometer pro Stunde.

Abbildung 1
(3 + 1 + 3 + 2 + 4 + 3 + 3 + 3 Punkte)
b)
Betrachtet wird die Schar der in  definierten Funktionen
definierten Funktionen  mit
mit
 und
und 


 . Dabei gibt
. Dabei gibt  mit
mit  die vergangene Zeit in Stunden ab der Entstehung des Staus und
die vergangene Zeit in Stunden ab der Entstehung des Staus und  die Staulänge in Kilometer an.
die Staulänge in Kilometer an.
 und
und 
(1)
Bestimme die lokalen Extremstellen von  und die Art dieser Extremstellen in Abhängigkeit von
und die Art dieser Extremstellen in Abhängigkeit von 
 Zur Kontrolle: Der einzige lokale Hochpunkt des Graphen von
Zur Kontrolle: Der einzige lokale Hochpunkt des Graphen von  befindet sich an der Stelle
befindet sich an der Stelle ![\(x=0,4 \cdot b .\big]\)](https://mathjax.schullv.de/1f7fead6bc542c63ba3d3baeeec0f4d355e97a990c208ce9b97c76b5c9bb189e?color=5a5a5a)
(2)
Für geeignete Parameter  und
und  ist die Funktion
ist die Funktion  identisch mit der Funktion
identisch mit der Funktion  (aus Aufgabenteil a)).
Bestimme die Parameter
(aus Aufgabenteil a)).
Bestimme die Parameter  und
und 
Eine Verkehrszentrale überwacht den Autobahnverkehr in der Umgebung. Die Computersysteme der Verkehrszentrale erhalten ständig Daten von Sensoren und Kameras, die von einer Software verarbeitet werden.
Die Software modelliert Staulängen mit den Funktionen
(3)
Auf einem Display wird ein Stau angezeigt, der um 06:00 Uhr entstanden ist. Für die Modellierung dieses Staus verwendet die Software die Parameter  und
und  Berechne den Zeitpunkt, zu dem die vorhergesagte Staulänge erstmals nach der Entstehung 10 Kilometer beträgt.
Berechne den Zeitpunkt, zu dem die vorhergesagte Staulänge erstmals nach der Entstehung 10 Kilometer beträgt.
Um 06:40 Uhr schaltet eine Mitarbeiterin der Verkehrszentrale eine Reihe von computergesteuerten Verkehrszeichen - ein sogenanntes Leitsystem - ein, die bei der Reduzierung des Staus helfen sollen. Dadurch ändern sich die Parameter der Modellierung für die Zeit nach 06:40 Uhr auf
(4)
Berechne, um wie viel Prozent die vorausgesagte maximale Staulänge durch das Einschalten des Leitsystems reduziert wird.
(5)
Zusätzlich zum Leitsystem soll ein Polizeieinsatz bei der Reduzierung des Staus helfen. Die Polizei will dafür sorgen, dass die Staulänge ab 11:00 Uhr konstant mit der Änderungsrate abnimmt, die die Software für 11:00 Uhr vorhersagt.
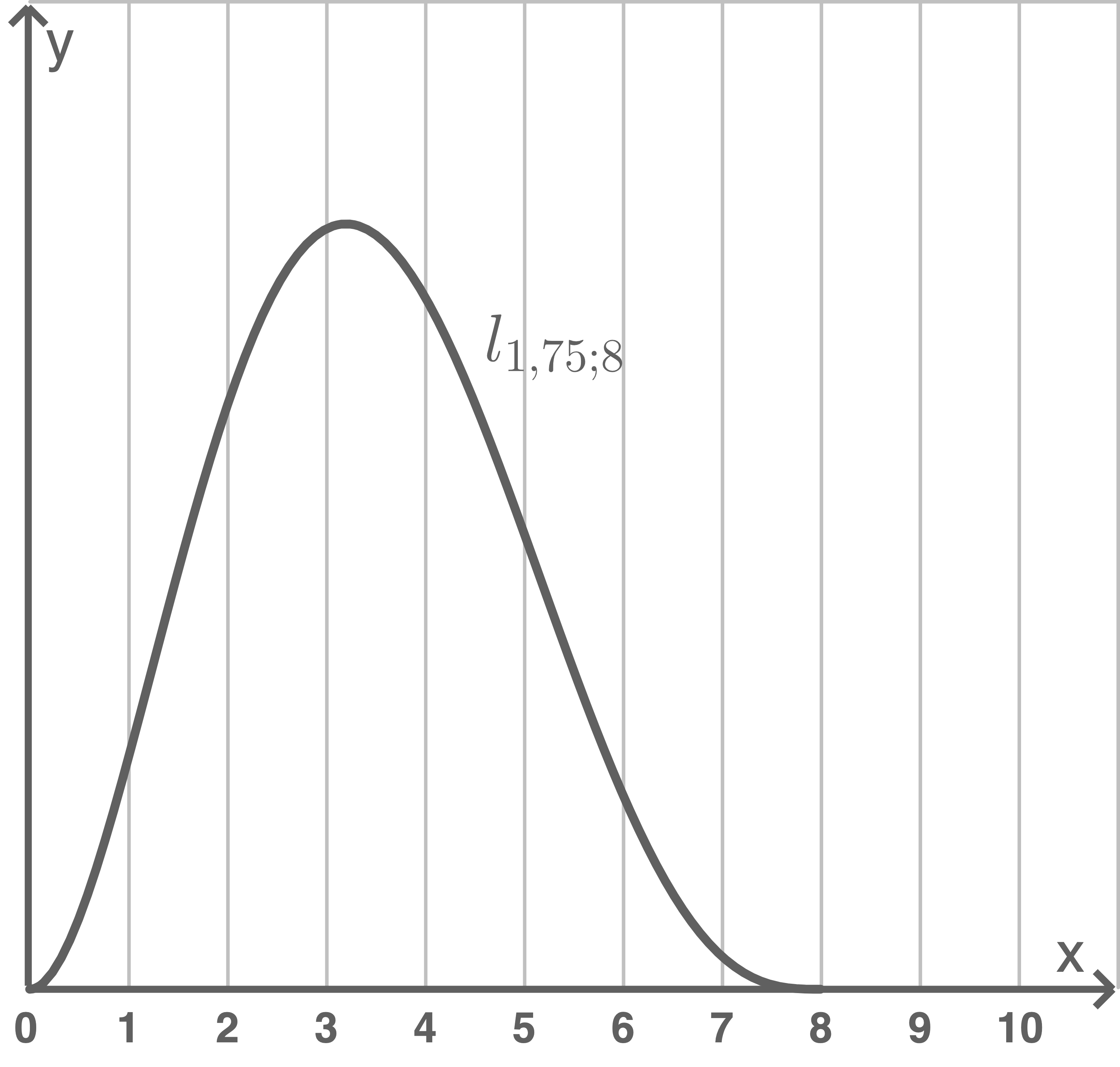
(i)
Ermittle unter diesen Voraussetzungen grafisch anhand von Abbildung 2, wann sich der Stau aufgelöst haben wird.
(ii)
Überprüfe dein Ergebnis aus (i) durch eine geeignete Rechnung.

Abbildung 2
(4 + 2 + 2 + 4 + 6 Punkte)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
(1)
Aus  folgt:
folgt:

 und
und  Dies entspricht den Zeitpunkten 06:00 Uhr, 07:36 Uhr und 10:00 Uhr.
Der Funktionsterm von
Dies entspricht den Zeitpunkten 06:00 Uhr, 07:36 Uhr und 10:00 Uhr.
Der Funktionsterm von  besteht aus vier Linearfaktoren, von denen zwei übereinstimmen. Damit kann
besteht aus vier Linearfaktoren, von denen zwei übereinstimmen. Damit kann  maximal drei Nullstellen besitzen und es gibt daher nur die oben genannten drei Zeitpunkte, zu denen die momentane Änderungsrate der Staulänge den Wert null hat.
maximal drei Nullstellen besitzen und es gibt daher nur die oben genannten drei Zeitpunkte, zu denen die momentane Änderungsrate der Staulänge den Wert null hat.
(2)
Um 08:00 Uhr nimmt die Staulänge ab.
(3)
Zeitpunkt mit der stärksten Zunahme bestimmen
Mit dem CAS wird das Maximum der Funktion  im Intervall
im Intervall ![\([0;4]\)](https://mathjax.schullv.de/1560f98ba45b1bf50e4254268fc3492c704d99f31b7a236afb4a70174b7d628e?color=5a5a5a) bestimmt. Daraus ergibt sich, dass das Maximum für
bestimmt. Daraus ergibt sich, dass das Maximum für  mit ca.
mit ca.  angenommen wird.
Die Staulänge nimmt also ca. 0,62 Stunden nach 06:00 Uhr am stärksten zu.
angenommen wird.
Die Staulänge nimmt also ca. 0,62 Stunden nach 06:00 Uhr am stärksten zu.
![\(0,62\cdot 60 = 37,2\;[\text{min}] \)](https://mathjax.schullv.de/7cc0bf1b36f83e50564a606fd199ce03cae831be45057fc6eca45122fb9732aa?color=5a5a5a) Um ca. 06:37 Uhr nimmt die Staulänge am stärksten zu.
Zeigen, dass
Um ca. 06:37 Uhr nimmt die Staulänge am stärksten zu.
Zeigen, dass  gilt
gilt





![\( \approx 2,17\;\left[\frac{\text{km}}{\text{h}}\right]\)](https://mathjax.schullv.de/a190c7a76daafd77d08047e5748678149f61333de573675639e983b331deecba?color=5a5a5a) Damit liegt die momentane Änderungsrate also zwischen
Damit liegt die momentane Änderungsrate also zwischen  und
und 
(4)
Der Stau ist um 07:36 Uhr am längsten.
Die Länge des Staus nimmt genau dann zu, wenn 
Dies ist zwischen der ersten und zweiten Nullstelle der Fall. Bis 07:36 Uhr nimmt die Staulänge daher zu und ab 07:36 Uhr bis 10:00 Uhr nimmt sie dann wieder ab.
Dies ist zwischen der ersten und zweiten Nullstelle der Fall. Bis 07:36 Uhr nimmt die Staulänge daher zu und ab 07:36 Uhr bis 10:00 Uhr nimmt sie dann wieder ab.
(5)
Aussage begründen
Die Funktion  modelliert die Änderungsrate der Staulänge im Zeitraum von 06:00 Uhr bis 10:00 Uhr. Die Staulänge wird also durch die Stammfunktion von
modelliert die Änderungsrate der Staulänge im Zeitraum von 06:00 Uhr bis 10:00 Uhr. Die Staulänge wird also durch die Stammfunktion von  beschrieben, die für
beschrieben, die für  den Wert null annimmt.
den Wert null annimmt.
![\(\begin{array}[t]{rll}
s](https://mathjax.schullv.de/9129ff06d2fa6dcf278b2640140061720bb3e33e0cb69fa1fecc33336cbb13bf?color=5a5a5a) Zudem gilt
Zudem gilt 


 Somit kann die Staulänge zu jedem Zeitpunkt von 06:00 Uhr bis 10:00 Uhr durch die Funktion
Somit kann die Staulänge zu jedem Zeitpunkt von 06:00 Uhr bis 10:00 Uhr durch die Funktion  angegeben werden.
Auflösung des Staus
Vier Stunden nach Entstehung des Staus ist es 10:00 Uhr, daraus folgt:
angegeben werden.
Auflösung des Staus
Vier Stunden nach Entstehung des Staus ist es 10:00 Uhr, daraus folgt:





![\( = 0 \;\text{[km]}\)](https://mathjax.schullv.de/bfbd87420b9cfc5ee4ed39c3365b5ca7ddb49bf10982a4aa0993866fd40abc93?color=5a5a5a)
(6)
Zunahme der Staulänge berechnen
![\(s(2)-s(0,5)\approx 2\;[\text{km}] - 0,7\;[\text{km}]\)](https://mathjax.schullv.de/7e91deeb9a850cf8b3f9e350b4d98a5d9be14b3ee62864240cd91b7067c0baf1?color=5a5a5a)
![\(= 1,3 \;[\text{km}]\)](https://mathjax.schullv.de/7cbaa96c2829949158409eea2754566735e1a3e20d194d7faa8b02e3758295da?color=5a5a5a) Die Länge des Staus hat zwischen 06:30 Uhr und 08:00 Uhr damit um ca.
Die Länge des Staus hat zwischen 06:30 Uhr und 08:00 Uhr damit um ca. ![\(1,3\;[\text{km}]\)](https://mathjax.schullv.de/f642c82c29c4e4c865267a3b221a6b763814b538ae339f62939adaa6f9c06896?color=5a5a5a) zugenommen.
Durchschnittliche Änderungsrate bestimmen
zugenommen.
Durchschnittliche Änderungsrate bestimmen

(7)
Gesucht ist der Zeitpunkt  mit
mit  Eingabe dieser Gleichung in den CAS und nach
Eingabe dieser Gleichung in den CAS und nach  auflösen liefert im Intervall
auflösen liefert im Intervall ![\([0;4]:\)](https://mathjax.schullv.de/3bf9f92bfa4fde4be89bcbe27e823c05dc63de560acef5998fc939adeb69093a?color=5a5a5a)

 Da
Da  und der Stau erst um 06:00 Uhr entsteht, ist
und der Stau erst um 06:00 Uhr entsteht, ist  der gesuchte Wert für
der gesuchte Wert für  Mit
Mit ![\(0,32\cdot60=19,2 \;[\text{min}]\)](https://mathjax.schullv.de/68f9f8044908d5254d4e9ba278f218ccbf5e7724cbf697e6fad53c415db4b3d3?color=5a5a5a) ist der gesuchte Zeitpunkt ca. 08:19 Uhr.
ist der gesuchte Zeitpunkt ca. 08:19 Uhr.
(8)
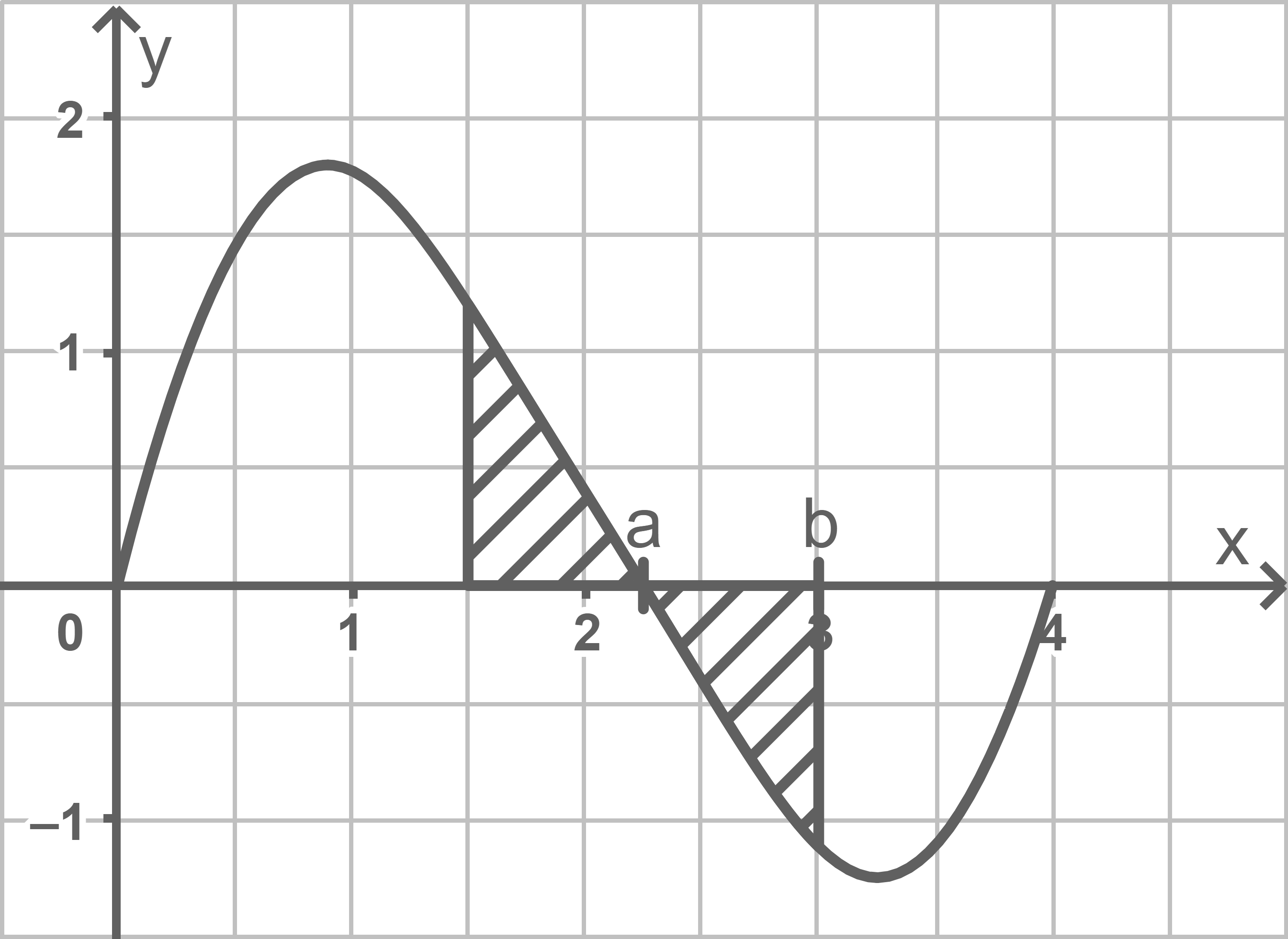
b)
(1)
1. Schritt: Notwendige Bedingung für Extremstellen anwenden
Mit dem CAS lässt sich die erste Ableitungsfunktion von  bestimmen und mit Null gleichsetzen:
bestimmen und mit Null gleichsetzen:
![\(\begin{array}[t]{rll}
l_{a;b}](https://mathjax.schullv.de/3cdf6d5f2baca6704e21e4d915104b0e70fe1892a8ddbdfdb0dc79051880f0cb?color=5a5a5a) 2. Schritt: Hinreichendes Kriterium für Extremstellen überprüfen
Mit dem CAS und mit
2. Schritt: Hinreichendes Kriterium für Extremstellen überprüfen
Mit dem CAS und mit  und
und  ergibt sich:
ergibt sich:


 3. Schritt: Art der Extremstellen ermitteln
Somit verfügt der Graph von
3. Schritt: Art der Extremstellen ermitteln
Somit verfügt der Graph von  an der Stelle
an der Stelle  über einen Tiefpunkt, an der Stelle
über einen Tiefpunkt, an der Stelle  über einen Hochpunkt und an der Stelle
über einen Hochpunkt und an der Stelle  über einen Sattelpunkt.
über einen Sattelpunkt.
(2)
Es ist  Daraus lassen sich die Nullstellen
Daraus lassen sich die Nullstellen  und
und  ablesen.
Die Nullstellen von
ablesen.
Die Nullstellen von  lassen sich ebenfalls mit dem Satz vom Nullprodukt bestimmen:
Es gilt
lassen sich ebenfalls mit dem Satz vom Nullprodukt bestimmen:
Es gilt 
![\(\begin{array}[t]{rll}
1- \dfrac{x}{b}&=& 0&\quad \scriptsize \mid\; -1 \\[5pt]
- \dfrac{x}{b}&=& -1&\quad \scriptsize \mid\; \cdot (-b)\\[5pt]
x_2 &=& b
\end{array}\)](https://mathjax.schullv.de/322bf819d4b415f685694b91196a0286376b82feb48705e43e78ed49c142741e?color=5a5a5a) Durch den Vergleich der beiden Nullstellen ergibt sich also
Durch den Vergleich der beiden Nullstellen ergibt sich also 
![\(\begin{array}[t]{rll}
0,4 \cdot b_s&=& 1,6&\quad \scriptsize \mid\;:0,4 \\[5pt]
b_s&=& 4
\end{array}\)](https://mathjax.schullv.de/ba38664da448bf3b444cee188182b60481f79ba81ddb1a244d368bab030bf8aa?color=5a5a5a) Gleichsetzen der Funktionsterme liefert mit dem CAS:
Gleichsetzen der Funktionsterme liefert mit dem CAS:
(3)
(4)
Mit den Parametern  und
und  und dem CAS ergibt sich das Maximum von
und dem CAS ergibt sich das Maximum von  zu ca.
zu ca.  Die vorhergesagte maximale Staulänge beträgt vor dem Einschalten des Leitsystems also ca. 15,9 Kilometer.
Für
Die vorhergesagte maximale Staulänge beträgt vor dem Einschalten des Leitsystems also ca. 15,9 Kilometer.
Für  und
und  ergibt sich ebenfalls mit Hilfe des CAS eine vorhergesagte maximale Staulänge von ca. 7,7 Kilometern.
ergibt sich ebenfalls mit Hilfe des CAS eine vorhergesagte maximale Staulänge von ca. 7,7 Kilometern.
 Die von der Software vorhergesagte Staulänge reduziert sich durch den Einsatz des Leitsystems um ca.
Die von der Software vorhergesagte Staulänge reduziert sich durch den Einsatz des Leitsystems um ca. 
(5)
(i)
Tangente an der Stelle  einzeichnen:
einzeichnen:
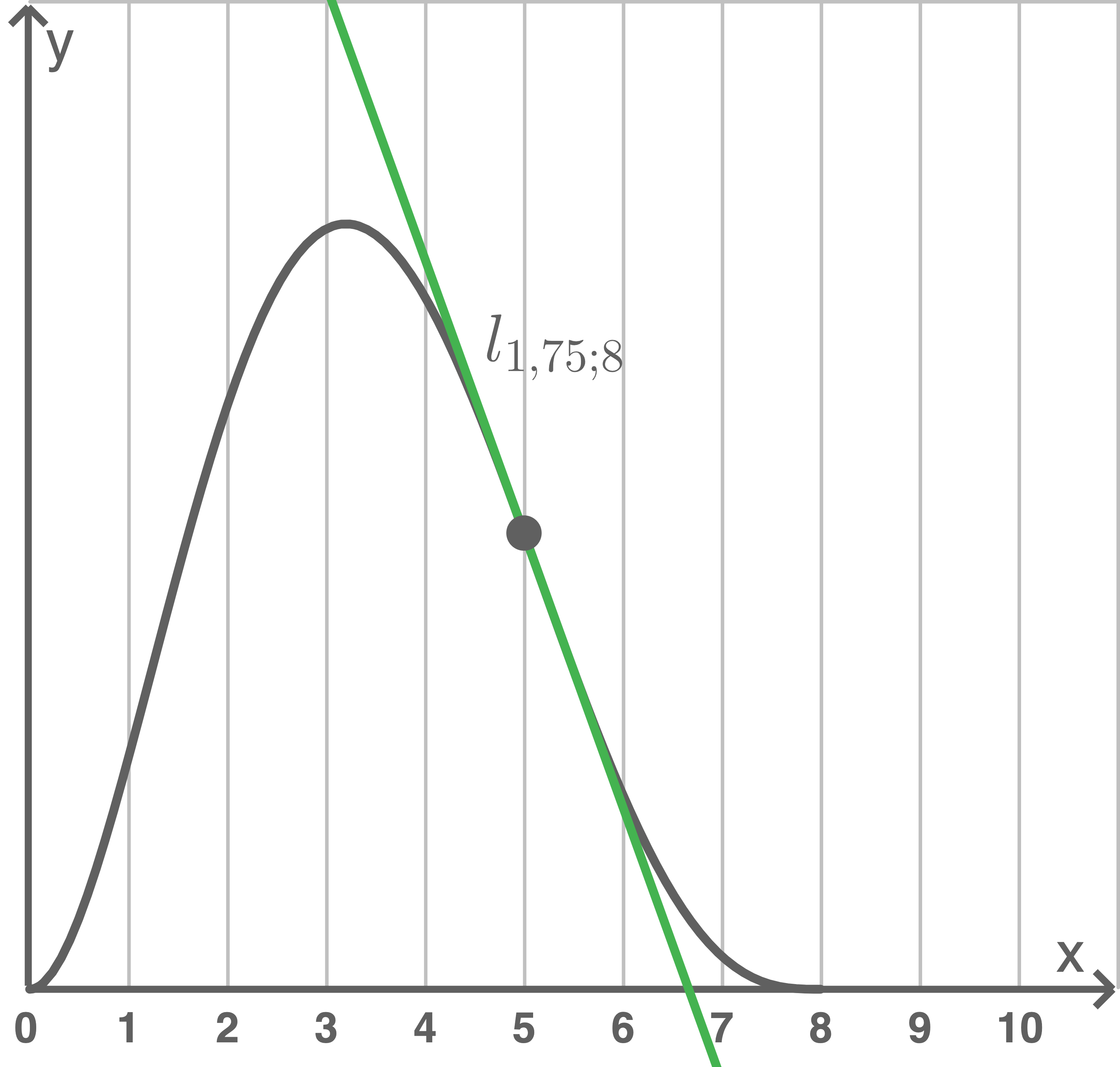 Nullstelle der Tangente:
Nullstelle der Tangente:  Folglich wird sich der Stau ca. gegen 12:40 Uhr aufgelöst haben.
Folglich wird sich der Stau ca. gegen 12:40 Uhr aufgelöst haben.

(ii)
Es gilt:

 Tangentengleichung aufstellen:
Tangentengleichung aufstellen:
![\(\begin{array}[t]{rll}
y_t&=&m\cdot x +b \\[5pt]
\dfrac{4725}{1024}&=&-\dfrac{2835}{1024}\cdot 5+b
\end{array}\)](https://mathjax.schullv.de/479ec83127f1623fb50fa67bc7f0c6969a0de36730e8e24cceb7409d8d5bc7f3?color=5a5a5a) Mit dem solve-Befehl des CAS ergibt sich
Mit dem solve-Befehl des CAS ergibt sich  Darus folgt
Darus folgt  Mit dem CAS folgt für
Mit dem CAS folgt für  dass die Tangente die
dass die Tangente die  -Achse bei
-Achse bei  schneidet.
Die Rechnung bestätigt, dass sich der Stau gegen 12:40 Uhr aufgelöst haben wird.
schneidet.
Die Rechnung bestätigt, dass sich der Stau gegen 12:40 Uhr aufgelöst haben wird.