A1
a)
Gegeben ist eine in  definierte Funktion
definierte Funktion  mit
mit  wobei
wobei  eine positive reelle Zahl ist. Abbildung 1 zeigt den Graphen von
eine positive reelle Zahl ist. Abbildung 1 zeigt den Graphen von 
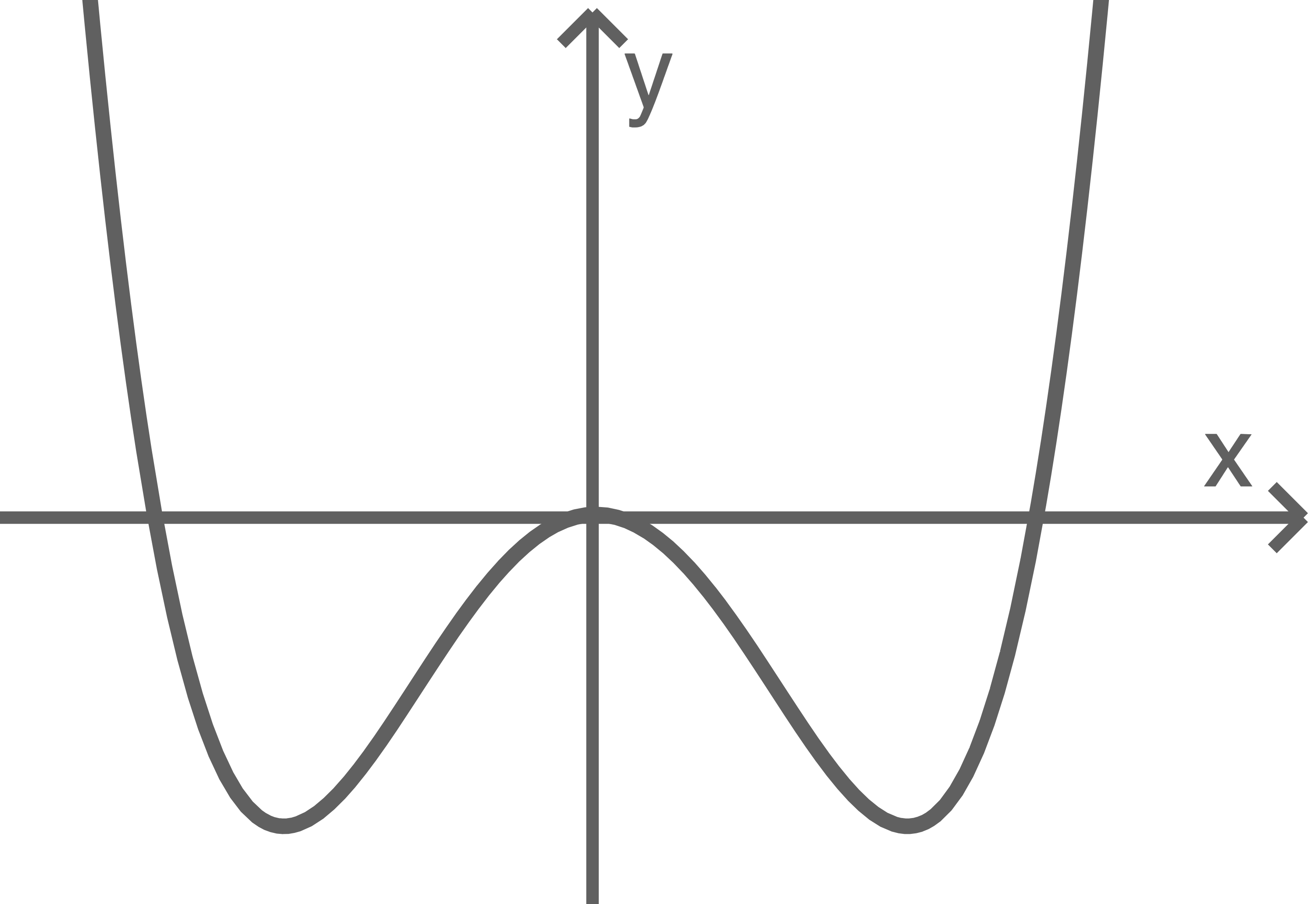

Abbildung 1
(1)
Zeige, dass  eine Gleichung der ersten Ableitungsfunktion von
eine Gleichung der ersten Ableitungsfunktion von  ist.
ist.
(2)
Die beiden Tiefpunkte des Graphen von  haben jeweils die
haben jeweils die  -Koordinate
-Koordinate  .
.
Ermittle den Wert von
Ermittle den Wert von
(1 + 4 Punkte)
b)
Die Funktion  ist gegeben durch
ist gegeben durch 
 Die Funktion
Die Funktion  ist eine Stammfunktion zur Funktion
ist eine Stammfunktion zur Funktion  Der Graph von
Der Graph von  ist in Abbildung 2 dargestellt.
ist in Abbildung 2 dargestellt.
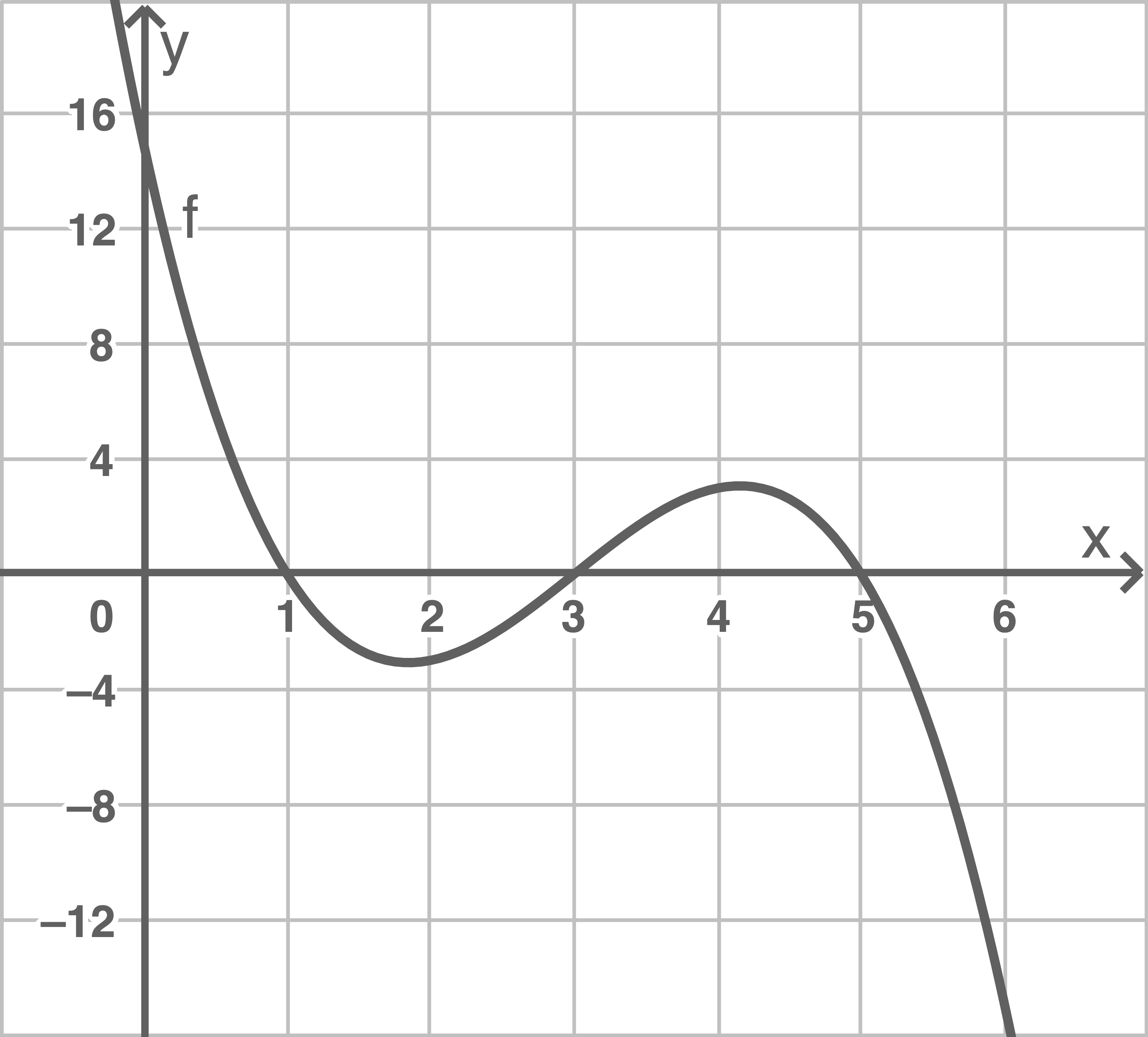

Abbildung 2
(1)
Interpretiere die Aussage  in Bezug auf den Graphen von
in Bezug auf den Graphen von 
(2)
Berechne 
(2 + 3 Punkte)
c)
Gegeben ist die Funktion  mit
mit  mit
mit 
Der Graph von ist in Abbildung 3 dargestellt.
ist in Abbildung 3 dargestellt.
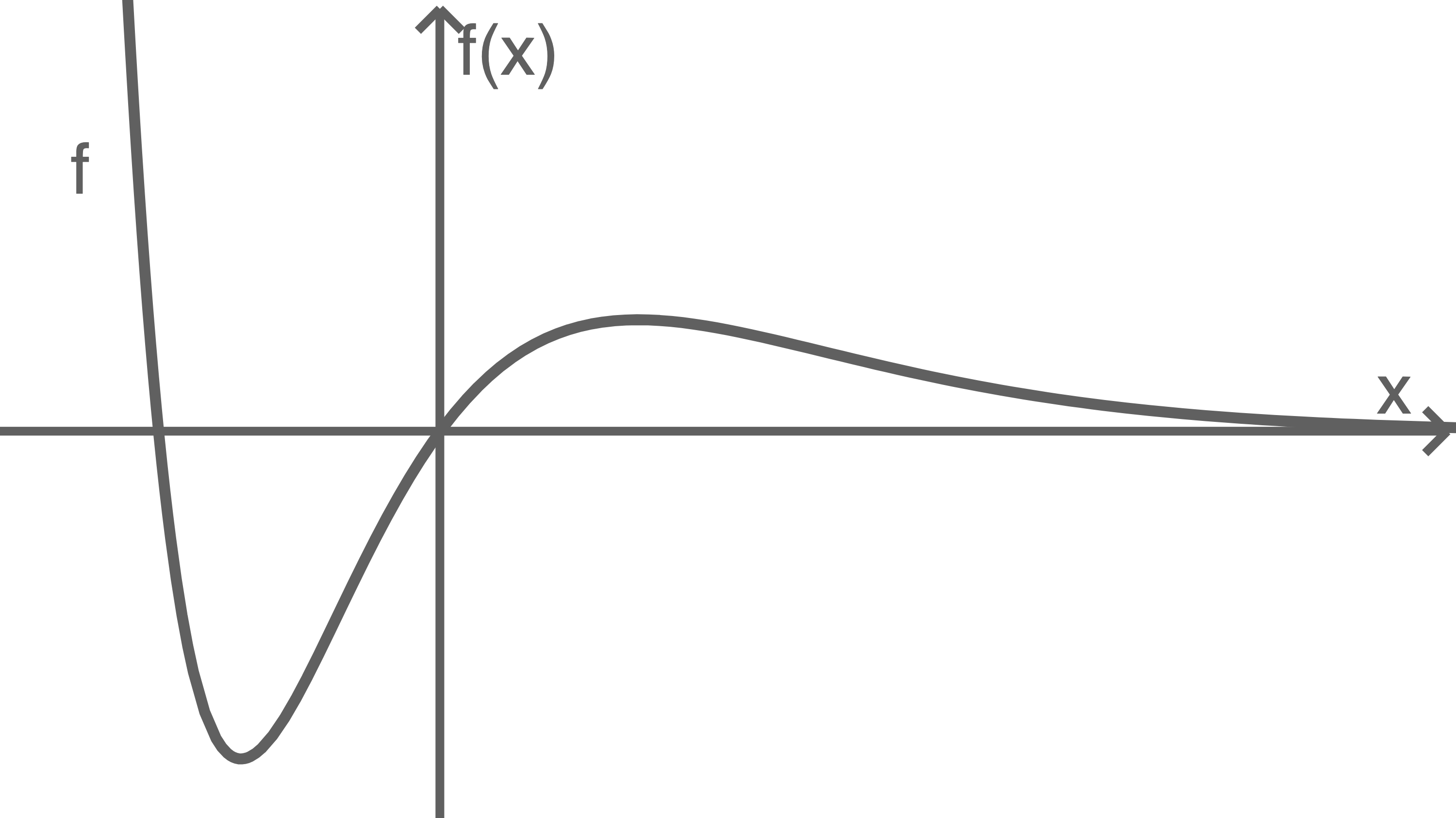
Der Graph von

Abbildung 3
(1)
Die Funktion  besitzt genau zwei Extremstellen.
besitzt genau zwei Extremstellen.
Ermittle die beiden Extremstellen von
Hinweis: Ein Nachweis der hinreichenden Bedingung ist nicht erforderlich.
Ermittle die beiden Extremstellen von
Hinweis: Ein Nachweis der hinreichenden Bedingung ist nicht erforderlich.
(2)
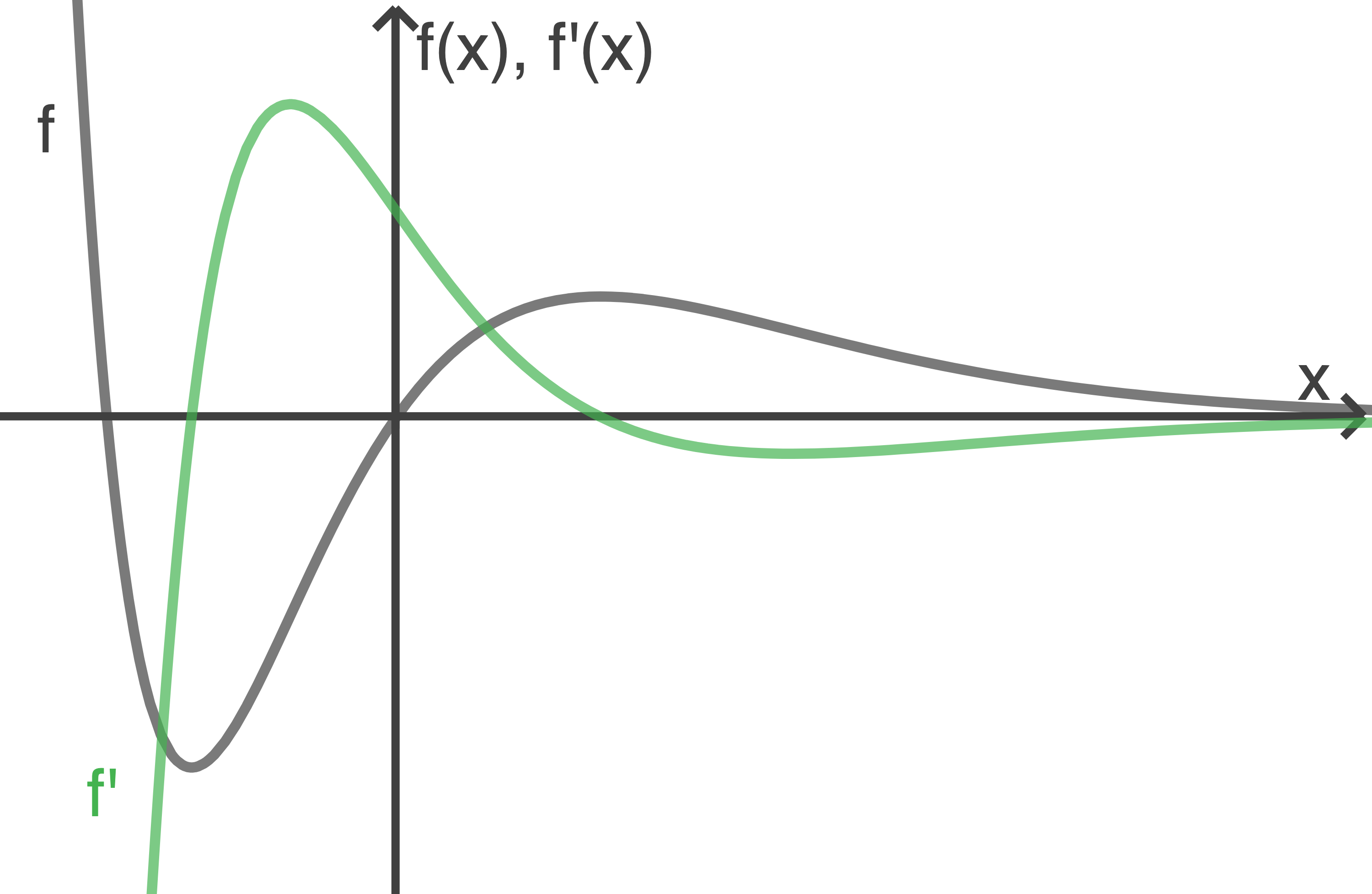
Skizziere in Abbildung 3 den Graphen der ersten Ableitungsfunktion von 
Hinweis: Die Größe der -Werte kann dabei unberücksichtigt bleiben.
-Werte kann dabei unberücksichtigt bleiben.
Hinweis: Die Größe der
(3 + 2 Punkte)
d)
Für jedes  ist durch die Gleichung
ist durch die Gleichung
 eine Funktion
eine Funktion  gegeben.
In Abbildung 4 ist der Graph der Funktion
gegeben.
In Abbildung 4 ist der Graph der Funktion  für
für  abgebildet.
abgebildet.
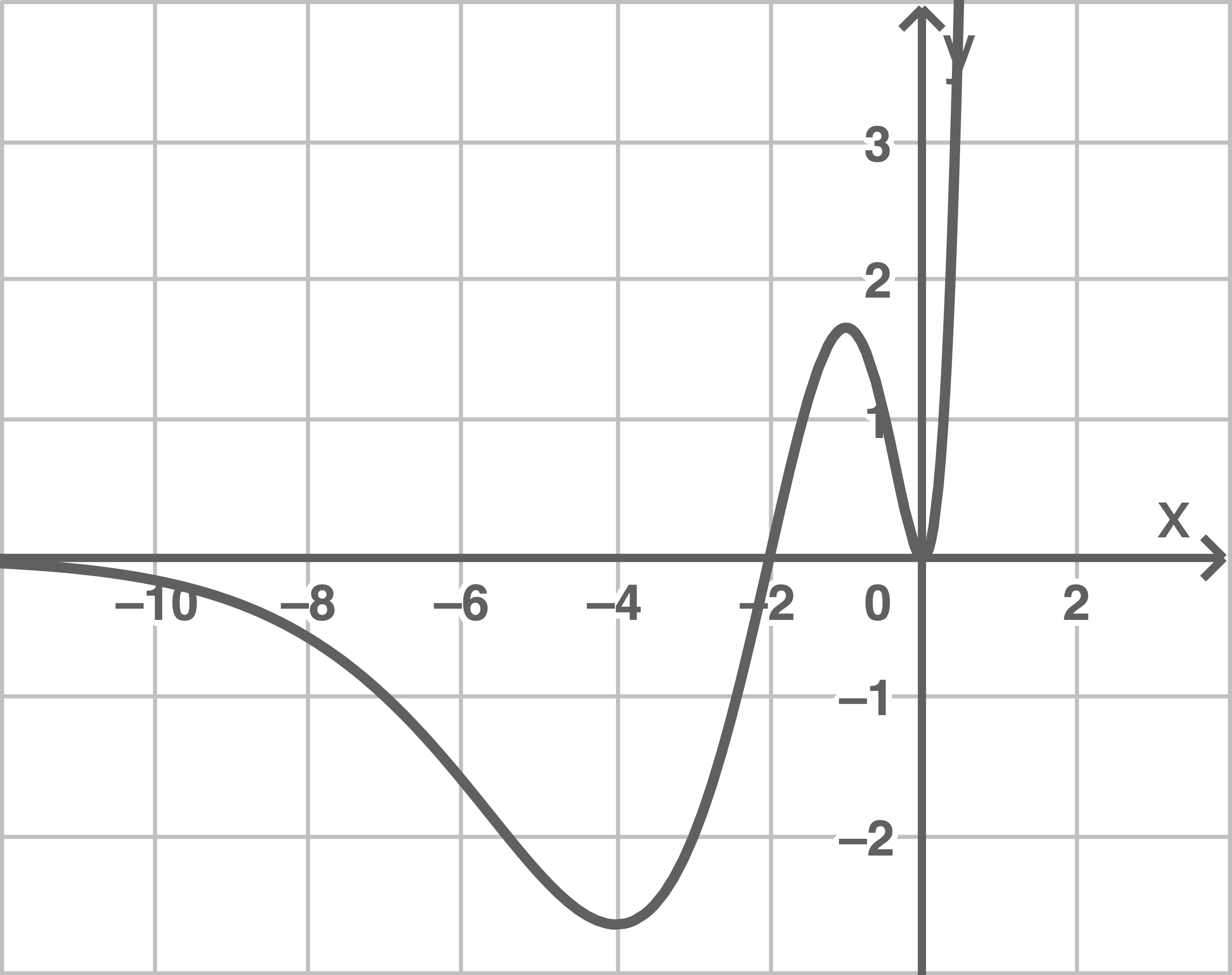

Abbildung 4
(1)
Es gibt genau einen Wert von  sodass die Funktion
sodass die Funktion  nur eine Nullstelle besitzt.
nur eine Nullstelle besitzt.
Ermittle diesen Wert von
Ermittle diesen Wert von
(2)
Ermittle, für welche Werte von  der Punkt
der Punkt  auf dem Graphen der Funktion
auf dem Graphen der Funktion  liegt.
liegt.
(2 + 3 Punkte)
e)
Betrachtet werden die Ebene  und für
und für  die Gerade
die Gerade  mit
mit 
(1)
Bestimme, denjenigen Wert von  für den die Gerade
für den die Gerade  senkrecht zu
senkrecht zu  steht.
steht.
(2)
Untersuche, ob es einen Wert von  gibt, für den die Gerade
gibt, für den die Gerade  in
in  liegt.
liegt.
(2 + 3 Punkte)
f)
Gegeben sind die Punkte  und
und 
(1)
Begründe, dass die Gerade durch  und
und  parallel zur
parallel zur  -Achse verläuft.
-Achse verläuft.
(2)
Der Punkt  liegt auf der
liegt auf der  -Achse. Die Gerade durch
-Achse. Die Gerade durch  und
und  steht senkrecht zur Geraden durch
steht senkrecht zur Geraden durch  und
und  Bestimme die Koordinaten aller Punkte, die die beschriebenen Eigenschaften des Punktes
Bestimme die Koordinaten aller Punkte, die die beschriebenen Eigenschaften des Punktes  haben.
haben.
(1 + 4 Punkte)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
(1)
(2)
Mit der notwendigen Bedingung für Extremstellen folgt:
![\(\begin{array}[t]{rlll}
f](https://mathjax.schullv.de/1af6f04ded1a895f0219b488904d2d8146ce8dadc2eb0fa1c263dfaa84e59cb4?color=5a5a5a) Mit dem Satz vom Nullprodukt folgt
Mit dem Satz vom Nullprodukt folgt  oder
oder 
![\(\begin{array}[t]{rll}
2x^2-k &= & 0 \quad \scriptsize \mid +k \mid :2\\[5pt]
x^2 &= & \frac{k}{2} \quad \scriptsize \mid \sqrt{\,\,} \\[5pt]
x_{2/3} &= & \pm \sqrt{\frac{k}{2}}& \quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/a3d588cb5dd0f67b2c73c3616d5abc0323849359d89ac7157f8521e07ac2e9eb?color=5a5a5a) Auf die hinreichende Bedingung kann verzichtet werden, weil aus der Aufgabe bekannt ist, dass es genau zwei Tiefpunkte gibt. Da nicht zwei Tiefpunkte aufeinander folgen können, muss bei
Auf die hinreichende Bedingung kann verzichtet werden, weil aus der Aufgabe bekannt ist, dass es genau zwei Tiefpunkte gibt. Da nicht zwei Tiefpunkte aufeinander folgen können, muss bei  ein Hochpunkt liegen und zwei Tiefpunkte bei
ein Hochpunkt liegen und zwei Tiefpunkte bei  liegen.
Es soll gelten
liegen.
Es soll gelten  und
und 
Für ergibt sich ebenfalls
ergibt sich ebenfalls  Da
Da  eine positive reelle Zahl sein soll, folgt
eine positive reelle Zahl sein soll, folgt 
Für
b)
(1)
Der Flächeninhalt der Fläche, die der Graph von  und die
und die  Achse im Intervall
Achse im Intervall ![\([1;3]\)](https://mathjax.schullv.de/4c871f3c45250ceb60647b58544ce3c3596fbc24341f187d6b6947c96521272c?color=5a5a5a) einschließt, ist genauso groß wie der Flächeninhalt der Fläche, die der Graph von
einschließt, ist genauso groß wie der Flächeninhalt der Fläche, die der Graph von  und die
und die  Achse im Intervall
Achse im Intervall ![\([3;5]\)](https://mathjax.schullv.de/9b74aa626c8d7e31a85e07aab7436e3c3c0ef3498047b88831b04d1ff79420d3?color=5a5a5a) einschließt.
einschließt.
(2)
c)
(1)
Mit der Produktregel folgt:


 Mit der notwendigen Bedingung für Extremstellen folgt:
Mit der notwendigen Bedingung für Extremstellen folgt:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/55d5f5177523770ba532807dd93c9276dfa26c35512511fa4c4325c04b1e7987?color=5a5a5a) Da
Da  ist, muss
ist, muss  gelten. Damit folgt:
gelten. Damit folgt:
![\(\begin{array}[t]{rll}
2-x^2&=& 0 \quad \scriptsize \mid \,+x^2\\[5pt]
2&=& x^2 \quad \scriptsize \\[5pt]
x^2&=& 2 \quad \scriptsize \mid \,\sqrt{\, \,}\\[5pt]
x_{1/2} &=& \pm \sqrt{2} & \quad \scriptsize\\[5pt]
\end{array}\)](https://mathjax.schullv.de/37d3f0fba8a35f2c3c7023273be86ebb24c40d8ac4917c4fe0944beeff9854db?color=5a5a5a) Die Extremstellen sind:
Die Extremstellen sind:  und
und 
(2)
d)
(1)
(2)
e)
(1)
(2)
f)
(1)
(2)
Für die Koordinaten eines Punktes  gilt
gilt  da
da  auf der
auf der  -Achse liegt. Da die Gerade durch
-Achse liegt. Da die Gerade durch  und
und  senkrecht zur Geraden durch
senkrecht zur Geraden durch  und
und  verläuft, muss folgendes gelten:
Die Koordinaten der Punkte, die die Eigenschaften des Punktes
verläuft, muss folgendes gelten:
Die Koordinaten der Punkte, die die Eigenschaften des Punktes  haben, sind
haben, sind  und
und 