Aufgabe 2
Aufgabenstellung
Eine Familie will ihren Bedarf an Wärmeenergie (thermischer Energie) für Heizung und Warmwasser teilweise durch eine thermische Solaranlage (kurz: Solaranlage) decken. Anhand der Angaben des Solaranlagenherstellers und der Verbrauchswerte der Familie aus dem letzten Kalenderjahr wurde das folgende Modell für ein beispielhaftes Kalenderjahr aufgestellt.
Die Leistung der Solaranlage wird durch die Funktion mit der Gleichung
mit der Gleichung
 ,
,  ,
und der thermische Leistungsbedarf der Familie (kurz: Leistungsbedarf) durch die Funktion
,
und der thermische Leistungsbedarf der Familie (kurz: Leistungsbedarf) durch die Funktion  mit der Gleichung
mit der Gleichung
 ,
,  ,
modelliert, und zwar für das Zeitintervall
,
modelliert, und zwar für das Zeitintervall ![\([0;12]\)](https://mathjax.schullv.de/5ba9b38204a320e9433651393178f89e741e0a72de8e09a0201574090d0733c6?color=5a5a5a) , das dem Kalenderjahr entspricht.
, das dem Kalenderjahr entspricht.
Dabei fasst man als Maßzahl zur Einheit
als Maßzahl zur Einheit  Monat und
Monat und  sowie
sowie  als Maßzahlen zur Einheit
als Maßzahlen zur Einheit  Kilowattstunde pro Monat [kWh/Monat] auf. (Im Modell umfasst jeder Monat
Kilowattstunde pro Monat [kWh/Monat] auf. (Im Modell umfasst jeder Monat  Tage.) Der Zeitpunkt
Tage.) Der Zeitpunkt  entspricht dem Beginn des Kalenderjahres.
entspricht dem Beginn des Kalenderjahres.
Die Graphen von und
und  sind in der Abbildung 1 unten dargestellt.
sind in der Abbildung 1 unten dargestellt.
 ist im Sachzusammenhang die aus der Solaranlage im Zeitintervall
ist im Sachzusammenhang die aus der Solaranlage im Zeitintervall ![\([a; b]\)](https://mathjax.schullv.de/55d9c86ce052c8cc565dcfb2a42d040a408cd01e6029a75d99c52b506b61c5b3?color=5a5a5a) abrufbare Energie und durch das Integral
abrufbare Energie und durch das Integral  der Energiebedarf der Familie im Zeitintervall
der Energiebedarf der Familie im Zeitintervall ![\([a; b]\)](https://mathjax.schullv.de/55d9c86ce052c8cc565dcfb2a42d040a408cd01e6029a75d99c52b506b61c5b3?color=5a5a5a) für
für  in Kilowattstunden [kWh] gegeben.
in Kilowattstunden [kWh] gegeben.

 ,
,  ,
,  ,
,
modelliert im Intervall [0;12] diese Leistung für ein Kalenderjahr, wobei der Parameter eine Kennzahl für die Neigung der Solarmodule ist. Jedem Wert des Parameters
eine Kennzahl für die Neigung der Solarmodule ist. Jedem Wert des Parameters  kann über die Gleichung
kann über die Gleichung  die Maßzahl für den entsprechenden Neigungswinkel in Grad zugeordnet werden.
die Maßzahl für den entsprechenden Neigungswinkel in Grad zugeordnet werden.
In der Abbildung 2 sind beispielhaft für zwei Werte von die Graphen der jeweils zugehörigen Funktion
die Graphen der jeweils zugehörigen Funktion  sowie der Graph von
sowie der Graph von  dargestellt.
dargestellt.
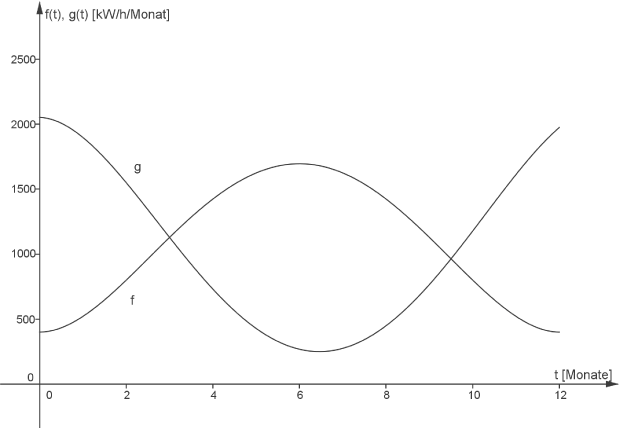 Abbildung 1
Abbildung 1
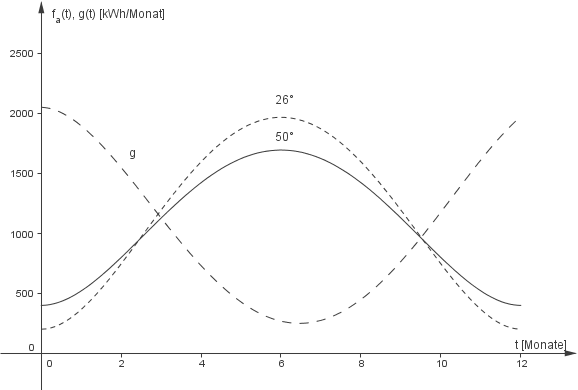 Abbildung 2
Abbildung 2
Die Leistung der Solaranlage wird durch die Funktion
Dabei fasst man
Die Graphen von
a) (1) Vergleiche die Graphen von  und
und  im Sachzusammenhang.
im Sachzusammenhang.
(5P)
(2) Bestimme den Zeitpunkt der maximalen Leistung der Solaranlage und berechne den Maximalwert.
(7P)
(3) Ermittle den Zeitpunkt im Intervall [ ], zu dem der durch
], zu dem der durch  beschriebene Leistungsbedarf der Familie innerhalb dieses Kalenderjahres am stärksten abnimmt.
beschriebene Leistungsbedarf der Familie innerhalb dieses Kalenderjahres am stärksten abnimmt.
(8P)
Durch das Integral
b) (1) Berechne den Energiebedarf der Familie für das Kalenderjahr.
(4P)
(2) Zu jedem Zeitpunkt, zu dem die Leistung der Solaranlage größer ist als der Leistungsbedarf der Familie, soll die „überschüssige“ Leistung zusätzlich zum Heizen eines Gartenpools genutzt werden.
Ermittle die Energie, die zum Heizen des Gartenpools in dem Kalenderjahr zur Verfügung steht.
(6P)
c) Die Leistung der Solaranlage ist abhängig von der Neigung der aufgestellten Solarmodule. Die Funktion  mit der Gleichung
mit der Gleichung

modelliert im Intervall [0;12] diese Leistung für ein Kalenderjahr, wobei der Parameter
In der Abbildung 2 sind beispielhaft für zwei Werte von
(1) Die Funktion  ist eine der Funktionen
ist eine der Funktionen  .
.
Ermittle für den zugehörigen Neigungswinkel
den zugehörigen Neigungswinkel  der Solarmodule.
der Solarmodule.
Ermittle für
(3P)
(2) Zeige, dass der Neigungswinkel stets einen Einfluss auf die Leistung der Solaranlage hat, d. h. dass es keinen Zeitpunkt  gibt, zu dem die Gleichung
gibt, zu dem die Gleichung  unabhängig vom Parameter
unabhängig vom Parameter  gilt.
gilt.
(5P)
(3) Weise nach, dass die in einem Jahr aus der Solaranlage abrufbare Energie für  (d.h.
(d.h.  ) am größten ist.
) am größten ist.
(6P)
(4) Der Solaranlagenhersteller behauptet, dass eine Solaranlage mit der Kennzahl  den Energiebedarf der Familie (ohne Heizung des Gartenpools!) in dem Kalenderjahr besser deckt als eine Solaranlage mit der Kennzahl
den Energiebedarf der Familie (ohne Heizung des Gartenpools!) in dem Kalenderjahr besser deckt als eine Solaranlage mit der Kennzahl  (vgl. Abbildung 2).
Überprüfe die Aussage rechnerisch.
(vgl. Abbildung 2).
Überprüfe die Aussage rechnerisch.
(6P)
 Abbildung 1
Abbildung 1
 Abbildung 2
Abbildung 2
a)(1)
 Graphen von
Graphen von  und
und  im Sachzusammenhang vergleichen
Hier sollst du die Graphen von
im Sachzusammenhang vergleichen
Hier sollst du die Graphen von  und
und  im Sachzusammenhang vergleichen. Die Funktion
im Sachzusammenhang vergleichen. Die Funktion  modelliert die Leistung der Solaranlage, die Funktion
modelliert die Leistung der Solaranlage, die Funktion  den Leistungsbedarf der Familie. Du erkennst, dass in den Intervallen
den Leistungsbedarf der Familie. Du erkennst, dass in den Intervallen ![\(\left[0;3\right]\)](https://mathjax.schullv.de/e6ac5d60749307c17b05c9a262850c1a1312bb0bdac1077886594150a0f01657?color=5a5a5a) und
und ![\(\left[9,5;12\right]\)](https://mathjax.schullv.de/47d231a407dc5122a8184c20a6aacccc109aaeff05e0642aed51402f3d886a66?color=5a5a5a) der Graph der Funktion
der Graph der Funktion  oberhalb des Graphen von
oberhalb des Graphen von  liegt, im Intervall
liegt, im Intervall ![\(\left[3;9,5\right]\)](https://mathjax.schullv.de/a03ac5fe1f2ee83bfa4590b6a6c79fbf40a569515ebcc534bfeed1e72a1f310a?color=5a5a5a) ist es gerade andersrum und der Graph von
ist es gerade andersrum und der Graph von  liegt über dem Graphen von
liegt über dem Graphen von  . Die Graphen von
. Die Graphen von  und
und  verhalten sich gegenläufig um einen Mittelwert von ca. 1.000.
Im Sachzusammenhang lässt sich dies so deuten, dass im Winter (Intervalle
verhalten sich gegenläufig um einen Mittelwert von ca. 1.000.
Im Sachzusammenhang lässt sich dies so deuten, dass im Winter (Intervalle ![\(\left[0;3\right]\)](https://mathjax.schullv.de/e6ac5d60749307c17b05c9a262850c1a1312bb0bdac1077886594150a0f01657?color=5a5a5a) und
und ![\(\left[9,5;12\right]\)](https://mathjax.schullv.de/47d231a407dc5122a8184c20a6aacccc109aaeff05e0642aed51402f3d886a66?color=5a5a5a) ) weniger Energie produziert wird als benötigt wird und die Solaranlage den Energiebedarf nicht vollständig deckt. Im Sommer (Intervall
) weniger Energie produziert wird als benötigt wird und die Solaranlage den Energiebedarf nicht vollständig deckt. Im Sommer (Intervall ![\(\left[3;9,5\right]\)](https://mathjax.schullv.de/a03ac5fe1f2ee83bfa4590b6a6c79fbf40a569515ebcc534bfeed1e72a1f310a?color=5a5a5a) ) wird mehr Energie als benötigt produziert und der Energiebedarf wird vollständig gedeckt.
Um den Juni (
) wird mehr Energie als benötigt produziert und der Energiebedarf wird vollständig gedeckt.
Um den Juni ( ) ist die Leistung der Solaranlage maximal und der Leistungsbedarf minimal. Um den Jahreswechsel (
) ist die Leistung der Solaranlage maximal und der Leistungsbedarf minimal. Um den Jahreswechsel ( bzw.
bzw.  ) ist die Leistung der Solaranlage minimal und der Leistungsbedarf maximal.
(2)
) ist die Leistung der Solaranlage minimal und der Leistungsbedarf maximal.
(2)
 Zeitpunkt maximaler Leistung der Solaranlage und Maximalwert bestimmen
Deine Aufgabe ist es den Zeitpunkt der maximalen Leistung der Solaranlage und den dazugehörigen Maximalwert zu bestimmen. Die Leistung der Solaranlage wird durch die Funktion
Zeitpunkt maximaler Leistung der Solaranlage und Maximalwert bestimmen
Deine Aufgabe ist es den Zeitpunkt der maximalen Leistung der Solaranlage und den dazugehörigen Maximalwert zu bestimmen. Die Leistung der Solaranlage wird durch die Funktion  beschrieben, also suchst du die Maximalstelle und den Maximalwert der Funktion
beschrieben, also suchst du die Maximalstelle und den Maximalwert der Funktion  . Diese kannst du mit dem CAS bestimmen. Eine Extremstelle einer Funktion ist durch die notwendige und hinreichende Bedingung bestimmt. Die Maximalstelle und den Maximalwert kannst du folgendermaßen berechnen:
. Diese kannst du mit dem CAS bestimmen. Eine Extremstelle einer Funktion ist durch die notwendige und hinreichende Bedingung bestimmt. Die Maximalstelle und den Maximalwert kannst du folgendermaßen berechnen:
 Die maximale Leistung der Solaranlage beträgt
Die maximale Leistung der Solaranlage beträgt  zum Zeitpunkt
zum Zeitpunkt  .
(3)
.
(3)
 Zeitpunkt der größten Abnahme des Leistungsbedarfs ermitteln
Gesucht ist der Zeitpunkt im Intervall
Zeitpunkt der größten Abnahme des Leistungsbedarfs ermitteln
Gesucht ist der Zeitpunkt im Intervall ![\([0;12]\)](https://mathjax.schullv.de/5ba9b38204a320e9433651393178f89e741e0a72de8e09a0201574090d0733c6?color=5a5a5a) , zu dem der durch
, zu dem der durch  beschriebene Leistungsbedarf am stärksten abnimmt. Dies kannst du auch folgendermaßen interpretieren:
Deine Aufgabe ist es den Zeitpunkt der maximalen Abnahme des Leistungsbedarfs und den dazugehörigen Wert zu bestimmen. Die Abnahme des Leistungsbedarfs wird durch die Ableitung der Funktion
beschriebene Leistungsbedarf am stärksten abnimmt. Dies kannst du auch folgendermaßen interpretieren:
Deine Aufgabe ist es den Zeitpunkt der maximalen Abnahme des Leistungsbedarfs und den dazugehörigen Wert zu bestimmen. Die Abnahme des Leistungsbedarfs wird durch die Ableitung der Funktion  beschrieben, also suchst du die Minimalstelle und den Minimalwert der Funktion
beschrieben, also suchst du die Minimalstelle und den Minimalwert der Funktion  . Diese kannst du mit dem CAS bestimmen. Eine Extremstelle einer Funktion ist durch die notwendige und hinreichende Bedingung bestimmt. Die Minimalstelle und den Minimalwert kannst du folgendermaßen berechnen:
. Diese kannst du mit dem CAS bestimmen. Eine Extremstelle einer Funktion ist durch die notwendige und hinreichende Bedingung bestimmt. Die Minimalstelle und den Minimalwert kannst du folgendermaßen berechnen:

 Zum Zeitpunkt
Zum Zeitpunkt  nimmt der Leistungsbedarf innerhalb des Kalenderjahres am stärksten ab.
nimmt der Leistungsbedarf innerhalb des Kalenderjahres am stärksten ab.
- Bestimme die erste und zweite Ableitung von
.
- Wende das notwendige Kriterium an. Für eine potenzielle Extremstelle
gilt:
Setze also
und löse nach
auf, um die möglichen Extremstellen zu bestimmen.
- Hinreichendes Kriterium überprüfen. Ist
für eine potenzielle Extremstelle
, so handelt es sich bei
um eine Maximalstelle. Setze die potenziellen Extremstellen in die zweite Ableitung ein und überprüfe das Ergebnis auf sein Vorzeichen.
- Den Maximalwert kannst du nun bestimmen, indem du die Maximalstelle in die Funktionsgleichung von
einsetzt.
1: Aktionen  1: Define , 3: Algebra
1: Define , 3: Algebra  1: Löse
1: Löse

- Bestimme die erste, zweite und dritte Ableitung von
.
- Wende das notwendige Kriterium an. Für eine potenzielle Extremstelle
gilt:
Setze also
und löse nach
auf, um die möglichen Extremstellen zu bestimmen.
- Hinreichendes Kriterium überprüfen. Ist
für eine potenzielle Extremstelle
, so handelt es sich bei
um eine Minimalstelle. Setze die potenziellen Extremstellen in die dritte Ableitung ein und überprüfe das Ergebnis auf sein Vorzeichen.
- Den Minimalwert kannst du nun bestimmen, indem du die Minimalstelle in die Funktionsgleichung von
einsetzt.


b)(1)
 Energiebedarf der Familie für das Kalenderjahr berechnen
Der Aufgabenstellung kannst du entnehmen, dass durch das Integral
Energiebedarf der Familie für das Kalenderjahr berechnen
Der Aufgabenstellung kannst du entnehmen, dass durch das Integral  der Energiebedarf der Familie im Zeitintervall
der Energiebedarf der Familie im Zeitintervall ![\([a;b]\)](https://mathjax.schullv.de/e84e12d6ffce2d83a82ceef8cfb5eb14688a4f4cce00a0d08d5357e2c6858142?color=5a5a5a) gegeben ist. Um den Energiebedarf für das Kalenderjahr zu berechnen, berechnest du das Integral mit den Grenzen
gegeben ist. Um den Energiebedarf für das Kalenderjahr zu berechnen, berechnest du das Integral mit den Grenzen  und
und  .
.
 Der Jahresbedarf an Energie der Familie beträgt in etwa
Der Jahresbedarf an Energie der Familie beträgt in etwa  .
(2)
.
(2)
 Berechnen der Energie, die zum Heizen des Pools zur Verfügung steht
Der Pool wird mit der Energie geheizt, welche den Bedarf der Familie übersteigt. Diese Energie ist gerade die Differenz zwischen der von der Solaranlage erzeugten Energie und dem Energiebedarf der Familie. Zum Zeitpunkt
Berechnen der Energie, die zum Heizen des Pools zur Verfügung steht
Der Pool wird mit der Energie geheizt, welche den Bedarf der Familie übersteigt. Diese Energie ist gerade die Differenz zwischen der von der Solaranlage erzeugten Energie und dem Energiebedarf der Familie. Zum Zeitpunkt  ist diese Leistung somit durch
ist diese Leistung somit durch  gegeben. Für die überschüssige Energie im Intervall
gegeben. Für die überschüssige Energie im Intervall ![\(\left[3;9,5\right]\)](https://mathjax.schullv.de/a03ac5fe1f2ee83bfa4590b6a6c79fbf40a569515ebcc534bfeed1e72a1f310a?color=5a5a5a) berechne das Integral
berechne das Integral  .
.
 Der Familie stehen somit
Der Familie stehen somit  kWh Energie zum Heizen des Pools zur Verfügung.
kWh Energie zum Heizen des Pools zur Verfügung.


c)(1)
 Zeigen, dass
Zeigen, dass  eine der Funktionen
eine der Funktionen  ist und zugehöriges
ist und zugehöriges  berechnen
Hier musst du ein
berechnen
Hier musst du ein ![\(a \in [0,5 1,5]\)](https://mathjax.schullv.de/b56df50ba3a9c59c14365fa29be93a514101a315c7da4bf0b8981756721496c0?color=5a5a5a) finden, sodass
finden, sodass  gilt. Schaue dir dazu die beiden Funktionsgleichungen an und leite anhand des Koeffizienten des Terms mit der höchsten Ordnung ein
gilt. Schaue dir dazu die beiden Funktionsgleichungen an und leite anhand des Koeffizienten des Terms mit der höchsten Ordnung ein  her, für das du die Behauptung überprüfst und das zugehörige
her, für das du die Behauptung überprüfst und das zugehörige  berechnest.
Da
berechnest.
Da  der Term der höchsten Ordnung von
der Term der höchsten Ordnung von  und
und  ist, wähle
ist, wähle  so, dass diese dieselben Koeffizienten besitzen, also
so, dass diese dieselben Koeffizienten besitzen, also  . Damit gilt:
. Damit gilt:
 Somit hast du die Behauptung nachgewiesen. Berechne nun das zugehörige
Somit hast du die Behauptung nachgewiesen. Berechne nun das zugehörige  :
:
![\(\begin{array}[t]{rll}
w=& 116 - 66 \cdot a & \scriptsize \mid\; a=1 \text{ einsetzen}
\\[5pt]
=& 116 - 66
\\[5pt]
=& 50
\end{array}\)](https://mathjax.schullv.de/6677b0536a070cf7a5456740899af5d73517a35fab98d182efa2f3441ee8d2f1?color=5a5a5a) Also beträgt der zugehörige Neigungswinkel
Also beträgt der zugehörige Neigungswinkel  .
(2)
.
(2)
 Zeige, dass
Zeige, dass  unabhängig von
unabhängig von  keine Lösung hat
Hier sollst du zeigen, dass die Gleichung
keine Lösung hat
Hier sollst du zeigen, dass die Gleichung  unabhängig von
unabhängig von  keine Lösung hat. Setze dazu ersetze dazu im Funktionsterm
keine Lösung hat. Setze dazu ersetze dazu im Funktionsterm 
 ein. Und setze die Funktionsterme der beiden Funktionen gleich.
ein. Und setze die Funktionsterme der beiden Funktionen gleich.
![\(\begin{array}[t]{rll}
f(t)&=&t^4-24t^3+144t^2+400\\[5pt]
f_a(t)&=&a\cdot(t^4-24t^3+144t^2+400)-400\cdot(a^2-1)\\[5pt]
&=&a\cdot f(t) -400\cdot (a^2-1)\\[5pt]
f(t_0)&=&f_a(t_0)\\[5pt]
f(t_0)&=&a\cdot f(t_0) -400\cdot (a^2-1)&\quad&\scriptsize\mid\; -f(t_0)\\[5pt]
0&=&f(t_0)\cdot(a-1)- 400\cdot (a^2-1)\\[5pt]
0&=&-400\cdot a^2 + f(t_0)\cdot a -f(t_0) +400\\[5pt]
\end{array}\)](https://mathjax.schullv.de/09eb5d1b85194839a1ad0ebfd85818fc2a187a9bf48b983490bbb2da8c01e8db?color=5a5a5a) Es zeigt sich, dass die Lösung der Gleichung von sogar quadratisch von
Es zeigt sich, dass die Lösung der Gleichung von sogar quadratisch von  abhängig ist.
(3)
abhängig ist.
(3)
 Maximum der Energie
Du sollst zeigen, dass für
Maximum der Energie
Du sollst zeigen, dass für  die durch die Solaranlage gewonnene Energie am größten ist. Die gewonnene Energie wird durch das Integral
die durch die Solaranlage gewonnene Energie am größten ist. Die gewonnene Energie wird durch das Integral  beschrieben. Man somit das Maximum der Funktion
beschrieben. Man somit das Maximum der Funktion  finden. Das kannst du mit dem CAS machen:
finden. Das kannst du mit dem CAS machen:
 Der CAS liefert
Der CAS liefert  . Somit ist die in einem Jahr maximale Energie aus der Solaranlage bei
. Somit ist die in einem Jahr maximale Energie aus der Solaranlage bei  .
(4)
.
(4)
 Behauptung des Solaranlagenherstellers begründen
Abbildung 2 liefert dir den Graphen
Behauptung des Solaranlagenherstellers begründen
Abbildung 2 liefert dir den Graphen  für den Neigungswinkel
für den Neigungswinkel  und den Graphen
und den Graphen  für
für  . Die von der Solaranlage mit dem entsprechenden Neigungswinkel bereitgestellte Energie wird durch die Flächen unterhalb der entsprechenden Graphen dargestellt. Zudem ist der Energiebedarf der Familie durch die Fläche unterhalb des Graphen der Funktion
. Die von der Solaranlage mit dem entsprechenden Neigungswinkel bereitgestellte Energie wird durch die Flächen unterhalb der entsprechenden Graphen dargestellt. Zudem ist der Energiebedarf der Familie durch die Fläche unterhalb des Graphen der Funktion  dargestellt.
Nun erkennst du anhand der Abbildung 2, dass die Fläche unterhalb des Graphen von
dargestellt.
Nun erkennst du anhand der Abbildung 2, dass die Fläche unterhalb des Graphen von  einen größeren Anteil an der Fläche unterhalb von
einen größeren Anteil an der Fläche unterhalb von  überdeckt als die Fläche unterhalb von
überdeckt als die Fläche unterhalb von  .
Damit deckt über das ganze Kalenderjahr die Solaranlage mit Neigungswinkel
.
Damit deckt über das ganze Kalenderjahr die Solaranlage mit Neigungswinkel  einen höheren Anteil am Leistungsbedarf der Familie als die Solaranlage mit Neigungswinkel
einen höheren Anteil am Leistungsbedarf der Familie als die Solaranlage mit Neigungswinkel  .
.
4: Analysis  8: Funktionsmaximum
8: Funktionsmaximum

a)(1)
 Graphen von
Graphen von  und
und  im Sachzusammenhang vergleichen
Hier sollst du die Graphen von
im Sachzusammenhang vergleichen
Hier sollst du die Graphen von  und
und  im Sachzusammenhang vergleichen. Die Funktion
im Sachzusammenhang vergleichen. Die Funktion  modelliert die Leistung der Solaranlage, die Funktion
modelliert die Leistung der Solaranlage, die Funktion  den Leistungsbedarf der Familie. Du erkennst, dass in den Intervallen
den Leistungsbedarf der Familie. Du erkennst, dass in den Intervallen ![\(\left[0;3\right]\)](https://mathjax.schullv.de/e6ac5d60749307c17b05c9a262850c1a1312bb0bdac1077886594150a0f01657?color=5a5a5a) und
und ![\(\left[9,5;12\right]\)](https://mathjax.schullv.de/47d231a407dc5122a8184c20a6aacccc109aaeff05e0642aed51402f3d886a66?color=5a5a5a) der Graph der Funktion
der Graph der Funktion  oberhalb des Graphen von
oberhalb des Graphen von  liegt, im Intervall
liegt, im Intervall ![\(\left[3;9,5\right]\)](https://mathjax.schullv.de/a03ac5fe1f2ee83bfa4590b6a6c79fbf40a569515ebcc534bfeed1e72a1f310a?color=5a5a5a) ist es gerade andersrum und der Graph von
ist es gerade andersrum und der Graph von  liegt über dem Graphen von
liegt über dem Graphen von  . Die Graphen von
. Die Graphen von  und
und  verhalten sich gegenläufig um einen Mittelwert von ca. 1.000.
Im Sachzusammenhang lässt sich dies so deuten, dass im Winter (Intervalle
verhalten sich gegenläufig um einen Mittelwert von ca. 1.000.
Im Sachzusammenhang lässt sich dies so deuten, dass im Winter (Intervalle ![\(\left[0;3\right]\)](https://mathjax.schullv.de/e6ac5d60749307c17b05c9a262850c1a1312bb0bdac1077886594150a0f01657?color=5a5a5a) und
und ![\(\left[9,5;12\right]\)](https://mathjax.schullv.de/47d231a407dc5122a8184c20a6aacccc109aaeff05e0642aed51402f3d886a66?color=5a5a5a) ) weniger Energie produziert wird als benötigt wird und die Solaranlage den Energiebedarf nicht vollständig deckt. Im Sommer (Intervall
) weniger Energie produziert wird als benötigt wird und die Solaranlage den Energiebedarf nicht vollständig deckt. Im Sommer (Intervall ![\(\left[3;9,5\right]\)](https://mathjax.schullv.de/a03ac5fe1f2ee83bfa4590b6a6c79fbf40a569515ebcc534bfeed1e72a1f310a?color=5a5a5a) ) wird mehr Energie als benötigt produziert und der Energiebedarf wird vollständig gedeckt.
Um den Juni (
) wird mehr Energie als benötigt produziert und der Energiebedarf wird vollständig gedeckt.
Um den Juni ( ) ist die Leistung der Solaranlage maximal und der Leistungsbedarf minimal. Um den Jahreswechsel (
) ist die Leistung der Solaranlage maximal und der Leistungsbedarf minimal. Um den Jahreswechsel ( bzw.
bzw.  ) ist die Leistung der Solaranlage minimal und der Leistungsbedarf maximal.
(2)
) ist die Leistung der Solaranlage minimal und der Leistungsbedarf maximal.
(2)
 Zeitpunkt maximaler Leistung der Solaranlage und Maximalwert bestimmen
Deine Aufgabe ist es den Zeitpunkt der maximalen Leistung der Solaranlage und den dazugehörigen Maximalwert zu bestimmen. Die Leistung der Solaranlage wird durch die Funktion
Zeitpunkt maximaler Leistung der Solaranlage und Maximalwert bestimmen
Deine Aufgabe ist es den Zeitpunkt der maximalen Leistung der Solaranlage und den dazugehörigen Maximalwert zu bestimmen. Die Leistung der Solaranlage wird durch die Funktion  beschrieben, also suchst du die Maximalstelle und den Maximalwert der Funktion
beschrieben, also suchst du die Maximalstelle und den Maximalwert der Funktion  . Diese kannst du mit dem CAS bestimmen. Eine Extremstelle einer Funktion ist durch die notwendige und hinreichende Bedingung bestimmt. Die Maximalstelle und den Maximalwert kannst du folgendermaßen berechnen:
. Diese kannst du mit dem CAS bestimmen. Eine Extremstelle einer Funktion ist durch die notwendige und hinreichende Bedingung bestimmt. Die Maximalstelle und den Maximalwert kannst du folgendermaßen berechnen:
 Die maximale Leistung der Solaranlage beträgt
Die maximale Leistung der Solaranlage beträgt  zum Zeitpunkt
zum Zeitpunkt  .
(3)
.
(3)
 Zeitpunkt der größten Abnahme des Leistungsbedarfs ermitteln
Gesucht ist der Zeitpunkt im Intervall
Zeitpunkt der größten Abnahme des Leistungsbedarfs ermitteln
Gesucht ist der Zeitpunkt im Intervall ![\([0;12]\)](https://mathjax.schullv.de/5ba9b38204a320e9433651393178f89e741e0a72de8e09a0201574090d0733c6?color=5a5a5a) , zu dem der durch
, zu dem der durch  beschriebene Leistungsbedarf am stärksten abnimmt. Dies kannst du auch folgendermaßen interpretieren:
Deine Aufgabe ist es den Zeitpunkt der maximalen Abnahme des Leistungsbedarfs und den dazugehörigen Wert zu bestimmen. Die Abnahme des Leistungsbedarfs wird durch die Ableitung der Funktion
beschriebene Leistungsbedarf am stärksten abnimmt. Dies kannst du auch folgendermaßen interpretieren:
Deine Aufgabe ist es den Zeitpunkt der maximalen Abnahme des Leistungsbedarfs und den dazugehörigen Wert zu bestimmen. Die Abnahme des Leistungsbedarfs wird durch die Ableitung der Funktion  beschrieben, also suchst du die Minimalstelle und den Minimalwert der Funktion
beschrieben, also suchst du die Minimalstelle und den Minimalwert der Funktion  . Diese kannst du mit dem CAS bestimmen. Eine Extremstelle einer Funktion ist durch die notwendige und hinreichende Bedingung bestimmt. Die Minimalstelle und den Minimalwert kannst du folgendermaßen berechnen:
. Diese kannst du mit dem CAS bestimmen. Eine Extremstelle einer Funktion ist durch die notwendige und hinreichende Bedingung bestimmt. Die Minimalstelle und den Minimalwert kannst du folgendermaßen berechnen:
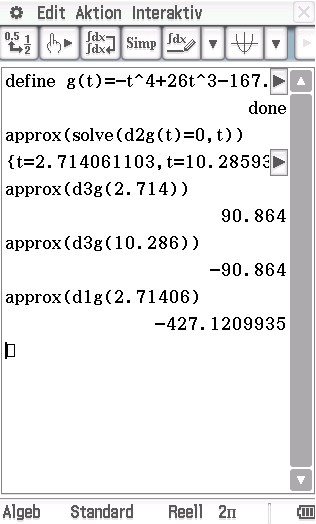 Zum Zeitpunkt
Zum Zeitpunkt  nimmt der Leistungsbedarf innerhalb des Kalenderjahres am stärksten ab.
nimmt der Leistungsbedarf innerhalb des Kalenderjahres am stärksten ab.
- Bestimme die erste und zweite Ableitung von
.
- Wende das notwendige Kriterium an. Für eine potenzielle Extremstelle
gilt:
Setze also
und löse nach
auf, um die möglichen Extremstellen zu bestimmen.
- Hinreichendes Kriterium überprüfen. Ist
für eine potenzielle Extremstelle
, so handelt es sich bei
um eine Maximalstelle. Setze die potenziellen Extremstellen in die zweite Ableitung ein und überprüfe das Ergebnis auf sein Vorzeichen.
- Den Maximalwert kannst du nun bestimmen, indem du die Maximalstelle in die Funktionsgleichung von
einsetzt.
Interaktiv  Define , Aktion
Define , Aktion  Weiterführend
Weiterführend  solve
solve

- Bestimme die erste, zweite und dritte Ableitung von
.
- Wende das notwendige Kriterium an. Für eine potenzielle Extremstelle
gilt:
Setze also
und löse nach
auf, um die möglichen Extremstellen zu bestimmen.
- Hinreichendes Kriterium überprüfen. Ist
für eine potenzielle Extremstelle
, so handelt es sich bei
um eine Minimalstelle. Setze die potenziellen Extremstellen in die dritte Ableitung ein und überprüfe das Ergebnis auf sein Vorzeichen.
- Den Minimalwert kannst du nun bestimmen, indem du die Minimalstelle in die Funktionsgleichung von
einsetzt.

b)(1)
 Energiebedarf der Familie für das Kalenderjahr berechnen
Der Aufgabenstellung kannst du entnehmen, dass durch das Integral
Energiebedarf der Familie für das Kalenderjahr berechnen
Der Aufgabenstellung kannst du entnehmen, dass durch das Integral  der Energiebedarf der Familie im Zeitintervall
der Energiebedarf der Familie im Zeitintervall ![\([a;b]\)](https://mathjax.schullv.de/e84e12d6ffce2d83a82ceef8cfb5eb14688a4f4cce00a0d08d5357e2c6858142?color=5a5a5a) gegeben ist. Um den Energiebedarf für das Kalenderjahr zu berechnen, berechnest du das Integral mit den Grenzen
gegeben ist. Um den Energiebedarf für das Kalenderjahr zu berechnen, berechnest du das Integral mit den Grenzen  und
und  .
.
 Der Jahresbedarf an Energie der Familie beträgt in etwa
Der Jahresbedarf an Energie der Familie beträgt in etwa  .
(2)
.
(2)
 Berechnen der Energie, die zum Heizen des Pools zur Verfügung steht
Der Pool wird mit der Energie geheizt, welche den Bedarf der Familie übersteigt. Diese Energie ist gerade die Differenz zwischen der von der Solaranlage erzeugten Energie und dem Energiebedarf der Familie. Zum Zeitpunkt
Berechnen der Energie, die zum Heizen des Pools zur Verfügung steht
Der Pool wird mit der Energie geheizt, welche den Bedarf der Familie übersteigt. Diese Energie ist gerade die Differenz zwischen der von der Solaranlage erzeugten Energie und dem Energiebedarf der Familie. Zum Zeitpunkt  ist diese Leistung somit durch
ist diese Leistung somit durch  gegeben. Für die überschüssige Energie im Intervall
gegeben. Für die überschüssige Energie im Intervall ![\(\left[3;9,5\right]\)](https://mathjax.schullv.de/a03ac5fe1f2ee83bfa4590b6a6c79fbf40a569515ebcc534bfeed1e72a1f310a?color=5a5a5a) berechne das Integral
berechne das Integral  .
.
 Der Familie stehen somit
Der Familie stehen somit  kWh Energie zum Heizen des Pools zur Verfügung.
kWh Energie zum Heizen des Pools zur Verfügung.


c)(1)
 Zeigen, dass
Zeigen, dass  eine der Funktionen
eine der Funktionen  ist und zugehöriges
ist und zugehöriges  berechnen
Hier musst du ein
berechnen
Hier musst du ein ![\(a \in [0,5 1,5]\)](https://mathjax.schullv.de/b56df50ba3a9c59c14365fa29be93a514101a315c7da4bf0b8981756721496c0?color=5a5a5a) finden, sodass
finden, sodass  gilt. Schaue dir dazu die beiden Funktionsgleichungen an und leite anhand des Koeffizienten des Terms mit der höchsten Ordnung ein
gilt. Schaue dir dazu die beiden Funktionsgleichungen an und leite anhand des Koeffizienten des Terms mit der höchsten Ordnung ein  her, für das du die Behauptung überprüfst und das zugehörige
her, für das du die Behauptung überprüfst und das zugehörige  berechnest.
Da
berechnest.
Da  der Term der höchsten Ordnung von
der Term der höchsten Ordnung von  und
und  ist, wähle
ist, wähle  so, dass diese dieselben Koeffizienten besitzen, also
so, dass diese dieselben Koeffizienten besitzen, also  . Damit gilt:
. Damit gilt:
 Somit hast du die Behauptung nachgewiesen. Berechne nun das zugehörige
Somit hast du die Behauptung nachgewiesen. Berechne nun das zugehörige  :
:
![\(\begin{array}[t]{rll}
w=& 116 - 66 \cdot a & \scriptsize \mid\; a=1 \text{ einsetzen}
\\[5pt]
=& 116 - 66
\\[5pt]
=& 50
\end{array}\)](https://mathjax.schullv.de/6677b0536a070cf7a5456740899af5d73517a35fab98d182efa2f3441ee8d2f1?color=5a5a5a) Also beträgt der zugehörige Neigungswinkel
Also beträgt der zugehörige Neigungswinkel  .
(2)
.
(2)
 Zeige, dass
Zeige, dass  unabhängig von
unabhängig von  keine Lösung hat
Hier sollst du zeigen, dass die Gleichung
keine Lösung hat
Hier sollst du zeigen, dass die Gleichung  unabhängig von
unabhängig von  keine Lösung hat. Setze dazu ersetze dazu im Funktionsterm
keine Lösung hat. Setze dazu ersetze dazu im Funktionsterm 
 ein. Und setze die Funktionsterme der beiden Funktionen gleich.
ein. Und setze die Funktionsterme der beiden Funktionen gleich.
![\(\begin{array}[t]{rll}
f(t)&=&t^4-24t^3+144t^2+400\\[5pt]
f_a(t)&=&a\cdot(t^4-24t^3+144t^2+400)-400\cdot(a^2-1)\\[5pt]
&=&a\cdot f(t) -400\cdot (a^2-1)\\[5pt]
f(t_0)&=&f_a(t_0)\\[5pt]
f(t_0)&=&a\cdot f(t_0) -400\cdot (a^2-1)&\quad&\scriptsize\mid\; -f(t_0)\\[5pt]
0&=&f(t_0)\cdot(a-1)- 400\cdot (a^2-1)\\[5pt]
0&=&-400\cdot a^2 + f(t_0)\cdot a -f(t_0) +400\\[5pt]
\end{array}\)](https://mathjax.schullv.de/09eb5d1b85194839a1ad0ebfd85818fc2a187a9bf48b983490bbb2da8c01e8db?color=5a5a5a) Es zeigt sich, dass die Lösung der Gleichung von sogar quadratisch von
Es zeigt sich, dass die Lösung der Gleichung von sogar quadratisch von  abhängig ist.
(3)
abhängig ist.
(3)
 Maximum der Energie
Du sollst zeigen, dass für
Maximum der Energie
Du sollst zeigen, dass für  die durch die Solaranlage gewonnene Energie am größten ist. Die gewonnene Energie wird durch das Integral
die durch die Solaranlage gewonnene Energie am größten ist. Die gewonnene Energie wird durch das Integral  beschrieben. Man somit das Maximum der Funktion
beschrieben. Man somit das Maximum der Funktion  finden. Das kannst du mit dem CAS machen:
finden. Das kannst du mit dem CAS machen:
 Der CAS liefert
Der CAS liefert  . Somit ist die in einem Jahr maximale Energie aus der Solaranlage bei
. Somit ist die in einem Jahr maximale Energie aus der Solaranlage bei  . (4)
. (4)
 Behauptung des Solaranlagenherstellers begründen
Abbildung 2 liefert dir den Graphen
Behauptung des Solaranlagenherstellers begründen
Abbildung 2 liefert dir den Graphen  für den Neigungswinkel
für den Neigungswinkel  und den Graphen
und den Graphen  für
für  . Die von der Solaranlage mit dem entsprechenden Neigungswinkel bereitgestellte Energie wird durch die Flächen unterhalb der entsprechenden Graphen dargestellt. Zudem ist der Energiebedarf der Familie durch die Fläche unterhalb des Graphen der Funktion
. Die von der Solaranlage mit dem entsprechenden Neigungswinkel bereitgestellte Energie wird durch die Flächen unterhalb der entsprechenden Graphen dargestellt. Zudem ist der Energiebedarf der Familie durch die Fläche unterhalb des Graphen der Funktion  dargestellt.
Nun erkennst du anhand der Abbildung 2, dass die Fläche unterhalb des Graphen von
dargestellt.
Nun erkennst du anhand der Abbildung 2, dass die Fläche unterhalb des Graphen von  einen größeren Anteil an der Fläche unterhalb von
einen größeren Anteil an der Fläche unterhalb von  überdeckt als die Fläche unterhalb von
überdeckt als die Fläche unterhalb von  .
Damit deckt über das ganze Kalenderjahr die Solaranlage mit Neigungswinkel
.
Damit deckt über das ganze Kalenderjahr die Solaranlage mit Neigungswinkel  einen höheren Anteil am Leistungsbedarf der Familie als die Solaranlage mit Neigungswinkel
einen höheren Anteil am Leistungsbedarf der Familie als die Solaranlage mit Neigungswinkel  .
.
Aktion  Berechnungen
Berechnungen  fMin/fMax
fMin/fMax  fMax
fMax
